Plücker coordinates

Short description: Method of assigning coordinates to every line in projective 3-space

In geometry, Plücker coordinates, introduced by Julius Plücker in the 19th century, are a way to assign six homogeneous coordinates to each line in projective 3-space, [math]\displaystyle{ \mathbb P^3 }[/math]. Because they satisfy a quadratic constraint, they establish a one-to-one correspondence between the 4-dimensional space of lines in [math]\displaystyle{ \mathbb P^3 }[/math] and points on a quadric in [math]\displaystyle{ \mathbb P^5 }[/math] (projective 5-space). A predecessor and special case of Grassmann coordinates (which describe k-dimensional linear subspaces, or flats, in an n-dimensional Euclidean space), Plücker coordinates arise naturally in geometric algebra. They have proved useful for computer graphics, and also can be extended to coordinates for the screws and wrenches in the theory of kinematics used for robot control.

Geometric intuition

Displacement and moment of two points on line

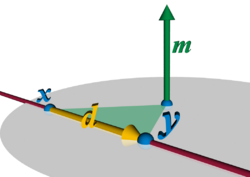
A line L in 3-dimensional Euclidean space is determined by two distinct points that it contains, or by two distinct planes that contain it. Consider the first case, with points [math]\displaystyle{ x=(x_1,x_2,x_3) }[/math] and [math]\displaystyle{ y=(y_1,y_2,y_3). }[/math] The vector displacement from x to y is nonzero because the points are distinct, and represents the direction of the line. That is, every displacement between points on L is a scalar multiple of d = y – x. If a physical particle of unit mass were to move from x to y, it would have a moment about the origin. The geometric equivalent to this moment, is a vector whose direction is perpendicular to the plane containing L and the origin, and whose length equals twice the area of the triangle formed by the displacement and the origin. Treating the points as displacements from the origin, the moment is m = x × y, where "×" denotes the vector cross product. For a fixed line, L, the area of the triangle is proportional to the length of the segment between x and y, considered as the base of the triangle; it is not changed by sliding the base along the line, parallel to itself. By definition the moment vector is perpendicular to every displacement along the line, so d ⋅ m = 0, where "⋅" denotes the vector dot product.

Although neither d nor m alone is sufficient to determine L, together the pair does so uniquely, up to a common (nonzero) scalar multiple which depends on the distance between x and y. That is, the coordinates

[math]\displaystyle{ (\mathbf d : \mathbf m ) = (d_1:d_2:d_3\ :\ m_1:m_2:m_3) }[/math]

may be considered homogeneous coordinates for L, in the sense that all pairs (λd : λm), for λ ≠ 0, can be produced by points on L and only L, and any such pair determines a unique line so long as d is not zero and d ⋅ m = 0. Furthermore, this approach extends to include points, lines, and a plane "at infinity", in the sense of projective geometry. In addition a point [math]\displaystyle{ x }[/math] lies on the line L if and only if [math]\displaystyle{ x \times d = m }[/math].

Example. Let x = (2, 3, 7) and y = (2, 1, 0). Then (d : m) = (0 : −2 : −7 : −7 : 14 : −4).

Alternatively, let the equations for points x of two distinct planes containing L be

[math]\displaystyle{ \begin{align} 0 &= a + \mathbf a \cdot \mathbf x, \\ 0 &= b + \mathbf b \cdot \mathbf x. \end{align} }[/math]

Then their respective planes are perpendicular to vectors a and b, and the direction of L must be perpendicular to both. Hence we may set d = a × b, which is nonzero because a, b are neither zero nor parallel (the planes being distinct and intersecting). If point x satisfies both plane equations, then it also satisfies the linear combination

[math]\displaystyle{ \begin{align} 0 &= a (b + \mathbf b \cdot \mathbf x) - b(a+ \mathbf a \cdot \mathbf x) \\ &= (a \mathbf b - b \mathbf a) \cdot \mathbf x \end{align} }[/math]

That is,

[math]\displaystyle{ \mathbf m = a \mathbf b - b \mathbf a }[/math]

is a vector perpendicular to displacements to points on L from the origin; it is, in fact, a moment consistent with the d previously defined from a and b.

Proof 1: Need to show that

[math]\displaystyle{ \mathbf m = a \mathbf b - b \mathbf a = \mathbf r \times \mathbf d = \mathbf r \times (\mathbf a \times \mathbf b). }[/math]^{what is "r"?}

Without loss of generality, let

[math]\displaystyle{ \mathbf a \cdot \mathbf a = \mathbf b \cdot \mathbf b = 1. }[/math]

Plane orthogonal to line L and including the origin.

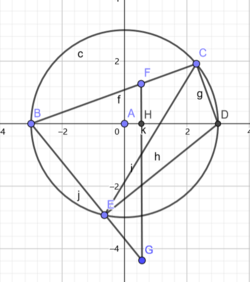
Point B is the origin. Line L passes through point D and is orthogonal to the plane of the picture. The two planes pass through CD and DE and are both orthogonal to the plane of the picture. Points C and E are the closest points on those planes to the origin B, therefore angles ∠ BCD and ∠ BED are right angles and so the points B, C, D, E lie on a circle (due to a corollary of Thales's theorem). BD is the diameter of that circle.

[math]\displaystyle{ \begin{align} & \mathbf a := \frac{BE}{||BE||}, \quad \mathbf b := \frac{BC}{||BC||}, \quad \mathbf r := BD; \\[4pt] & - \! a = ||BE|| = ||BF||, \quad -b = ||BC|| = ||BG||; \\[4pt] & \mathbf m = a \mathbf b - b \mathbf a = FG \\[4pt] & || \mathbf d || = || \mathbf a \times \mathbf b || = \sin\angle FBG \end{align} }[/math]

Angle ∠ BHF is a right angle due to the following argument. Let ε := ∠ BEC. Since △ BEC ≅ △ BFG (by side-angle-side congruence), then ∠ BFG = ε. Since ∠ BEC + ∠ CED = 90°, let ε' := 90° – ε = ∠ CED. By the inscribed angle theorem, ∠ DEC = ∠ DBC, so ∠ DBC = ε'. ∠ HBF + ∠ BFH + ∠ FHB = 180°; ε' + ε + ∠ FHB = 180°, ε + ε' = 90°; therefore, ∠ FHB = 90°. Then ∠ DHF must be a right angle as well.

Angles ∠ DCF, ∠ DHF are right angles, so the four points C, D, H, F lie on a circle, and (by the intersecting secants theorem)

[math]\displaystyle{ ||BF|| \, ||BC|| = ||BH|| \, ||BD|| }[/math]

that is,

[math]\displaystyle{ \begin{align} &ab \sin\angle FBG = ||BH|| \, || \mathbf r || \sin\angle FBG , \\[4pt] & 2 \, \text{Area}_{\triangle BFG} = ab \sin\angle FBG = ||BH|| \, ||FG|| = ||BH|| \, || \mathbf r || \sin\angle FBG, \\[4pt] & || \mathbf m || = ||FG|| = || \mathbf r || \sin\angle FBG = || \mathbf r || \, || \mathbf d ||, \\[4pt] & \mathbf m = \mathbf r \times \mathbf d. \blacksquare \end{align} }[/math]

Proof 2:

Let

[math]\displaystyle{ \mathbf a \cdot \mathbf a = \mathbf b \cdot \mathbf b = 1. }[/math]

This implies that

[math]\displaystyle{ a = -||BE||, \quad b = -||BC||. }[/math]

According to the vector triple product formula,

[math]\displaystyle{ \mathbf r \times (\mathbf a \times \mathbf b) = (\mathbf r \cdot \mathbf b) \mathbf a - (\mathbf r \cdot \mathbf a) \mathbf b. }[/math]

Then

[math]\displaystyle{ \begin{align} \mathbf r \times (\mathbf a \times \mathbf b) &= \mathbf a \, || \mathbf r || \, || \mathbf b || \cos\angle DBC - \mathbf b \, ||\mathbf r || \, || \mathbf a || \cos\angle DBE \\[4pt] &= \mathbf a \, || \mathbf r || \cos\angle DBC - \mathbf b \, || \mathbf r || \cos\angle DBE \\[4pt] &= \mathbf a \, || BC || - \mathbf b \, || BE || \\[4pt] &= -b \mathbf a - (-a) \mathbf b \\[4pt] &= a \mathbf b - b \mathbf a\ \ \blacksquare \end{align} }[/math]

When [math]\displaystyle{ || \mathbf r || = 0, }[/math] the line L passes the origin with direction d. If [math]\displaystyle{ || \mathbf r || \gt 0, }[/math] the line has direction d; the plane that includes the origin and the line L has normal vector m; the line is tangent to a circle on that plane (normal to m and perpendicular to the plane of the picture) centered at the origin and with radius [math]\displaystyle{ || \mathbf r ||. }[/math]

Example. Let a₀ = 2, a = (−1, 0, 0) and b₀ = −7, b = (0, 7, −2). Then (d : m) = (0 : −2 : −7 : −7 : 14 : −4).

Although the usual algebraic definition tends to obscure the relationship, (d : m) are the Plücker coordinates of L.

Algebraic definition

Primal coordinates

In a 3-dimensional projective space [math]\displaystyle{ \mathbb P^3 }[/math], let L be a line through distinct points x and y with homogenous coordinates (x₀ : x₁ : x₂ : x₃) and (y₀ : y₁ : y₂ : y₃).

The Plücker coordinates p_ij are defined as follows:

[math]\displaystyle{ p_{ij} = \begin{vmatrix} x_{i} & y_{i} \\ x_{j} & y_{j}\end{vmatrix} = x_{i}y_{j}-x_{j}y_{i} . }[/math]

(the skew symmetric matrix whose elements are p_ij is also called the Plücker matrix )
This implies p_ii = 0 and p_ij = −p_ji, reducing the possibilities to only six (4 choose 2) independent quantities. The sextuple

[math]\displaystyle{ (p_{01}:p_{02}:p_{03}:p_{23}:p_{31}:p_{12}) }[/math]

is uniquely determined by L up to a common nonzero scale factor. Furthermore, not all six components can be zero. Thus the Plücker coordinates of L may be considered as homogeneous coordinates of a point in a 5-dimensional projective space, as suggested by the colon notation.

To see these facts, let M be the 4×2 matrix with the point coordinates as columns.

[math]\displaystyle{ M = \begin{bmatrix} x_0 & y_0 \\ x_1 & y_1 \\ x_2 & y_2 \\ x_3 & y_3 \end{bmatrix} }[/math]

The Plücker coordinate p_ij is the determinant of rows i and j of M. Because x and y are distinct points, the columns of M are linearly independent; M has rank 2. Let M′ be a second matrix, with columns x′, y′ a different pair of distinct points on L. Then the columns of M′ are linear combinations of the columns of M; so for some 2×2 nonsingular matrix Λ,

[math]\displaystyle{ M' = M\Lambda . }[/math]

In particular, rows i and j of M′ and M are related by

[math]\displaystyle{ \begin{bmatrix} x'_{i} & y'_{i}\\x'_{j}& y'_{j} \end{bmatrix} = \begin{bmatrix} x_{i} & y_{i}\\x_{j}& y_{j} \end{bmatrix} \begin{bmatrix} \lambda_{00} & \lambda_{01} \\ \lambda_{10} & \lambda_{11} \end{bmatrix} . }[/math]

Therefore, the determinant of the left side 2×2 matrix equals the product of the determinants of the right side 2×2 matrices, the latter of which is a fixed scalar, det Λ. Furthermore, all six 2×2 subdeterminants in M cannot be zero because the rank of M is 2.

Plücker map

Denote the set of all lines (linear images of [math]\displaystyle{ \mathbb P^1 }[/math]) in [math]\displaystyle{ \mathbb P^3 }[/math] by G_1,3. We thus have a map:

[math]\displaystyle{ \begin{align} \alpha \colon \mathrm{G}_{1,3} & \rightarrow \mathbb P^5 \\ L & \mapsto L^{\alpha}, \end{align} }[/math]

where

[math]\displaystyle{ L^{\alpha}=(p_{01}:p_{02}:p_{03}:p_{23}:p_{31}:p_{12}) . }[/math]

Dual coordinates

Alternatively, a line can be described as the intersection of two planes. Let L be a line contained in distinct planes a and b with homogeneous coefficients (a⁰ : a¹ : a² : a³) and (b⁰ : b¹ : b² : b³), respectively. (The first plane equation is [math]\displaystyle{ \sum_k a^k x_k =0, }[/math] for example.) The dual Plücker coordinate p^ij is

[math]\displaystyle{ p^{ij} = \begin{vmatrix} a^{i} & a^{j} \\ b^{i} & b^{j}\end{vmatrix} = a^{i}b^{j}-a^{j}b^{i} . }[/math]

Dual coordinates are convenient in some computations, and they are equivalent to primary coordinates:

[math]\displaystyle{ (p_{01}:p_{02}:p_{03}:p_{23}:p_{31}:p_{12})= (p^{23}:p^{31}:p^{12}:p^{01}:p^{02}:p^{03}) }[/math]

Here, equality between the two vectors in homogeneous coordinates means that the numbers on the right side are equal to the numbers on the left side up to some common scaling factor λ. Specifically, let (i, j, k, ℓ) be an even permutation of (0, 1, 2, 3); then

[math]\displaystyle{ p_{ij} = \lambda p^{k\ell} . }[/math]

Geometry

To relate back to the geometric intuition, take x₀ = 0 as the plane at infinity; thus the coordinates of points not at infinity can be normalized so that x₀ = 1. Then M becomes

[math]\displaystyle{ M = \begin{bmatrix} 1 & 1 \\ x_1 & y_1 \\ x_2& y_2 \\ x_3 & y_3 \end{bmatrix} , }[/math]

and setting [math]\displaystyle{ x=(x_1,x_2,x_3) }[/math] and [math]\displaystyle{ y=(y_1,y_2,y_3) }[/math], we have [math]\displaystyle{ d=(p_{01},p_{02},p_{03}) }[/math]and [math]\displaystyle{ m=(p_{23},p_{31},p_{12}) }[/math].

Dually, we have [math]\displaystyle{ d=(p^{23},p^{31},p^{12}) }[/math] and [math]\displaystyle{ m=(p^{01},p^{02},p^{03}). }[/math]

Bijection between lines and Klein quadric

Plane equations

If the point [math]\displaystyle{ \mathbf z = (z_0:z_1:z_2:z_3) }[/math] lies on L, then the columns of

[math]\displaystyle{ \begin{bmatrix} x_0 & y_0 & z_0 \\ x_1 & y_1 & z_1 \\ x_2 & y_2 & z_2 \\ x_3 & y_3 & z_3 \end{bmatrix} }[/math]

are linearly dependent, so that the rank of this larger matrix is still 2. This implies that all 3×3 submatrices have determinant zero, generating four (4 choose 3) plane equations, such as

[math]\displaystyle{ \begin{align} 0 & = \begin{vmatrix} x_0 & y_0 & z_0 \\ x_1 & y_1 & z_1 \\ x_2 & y_2 & z_2 \end{vmatrix} \\[5pt] & = \begin{vmatrix} x_1 & y_1 \\ x_2 & y_2 \end{vmatrix} z_0 - \begin{vmatrix} x_0 & y_0 \\ x_2 & y_2 \end{vmatrix} z_1 + \begin{vmatrix} x_0 & y_0 \\ x_1 & y_1 \end{vmatrix} z_2 \\[5pt] & = p_{12} z_0 - p_{02} z_1 + p_{01} z_2 . \\[5pt] & = p^{03} z_0 + p^{13} z_1 + p^{23} z_2 . \end{align} }[/math]

The four possible planes obtained are as follows.

[math]\displaystyle{ \begin{matrix} 0 & = & {}+ p_{12} z_0 & {}- p_{02} z_1 & {}+ p_{01} z_2 & \\ 0 & = & {}- p_{31} z_0 & {}- p_{03} z_1 & & {}+ p_{01} z_3 \\ 0 & = & {}+p_{23} z_0 & & {}- p_{03} z_2 & {}+ p_{02} z_3 \\ 0 & = & & {}+p_{23} z_1 & {}+ p_{31} z_2 & {}+ p_{12} z_3 \end{matrix} }[/math]

Using dual coordinates, and letting (a⁰ : a¹ : a² : a³) be the line coefficients, each of these is simply aⁱ = p^ij, or

[math]\displaystyle{ 0 = \sum_{i=0}^3 p^{ij} z_i , \qquad j = 0,\ldots,3 . }[/math]

Each Plücker coordinate appears in two of the four equations, each time multiplying a different variable; and as at least one of the coordinates is nonzero, we are guaranteed non-vacuous equations for two distinct planes intersecting in L. Thus the Plücker coordinates of a line determine that line uniquely, and the map α is an injection.

Quadratic relation

The image of α is not the complete set of points in [math]\displaystyle{ \mathbb P^5 }[/math]; the Plücker coordinates of a line L satisfy the quadratic Plücker relation

[math]\displaystyle{ \begin{align} 0 & = p_{01}p^{01}+p_{02}p^{02}+p_{03}p^{03} \\ & = p_{01}p_{23}+p_{02}p_{31}+p_{03}p_{12}. \end{align} }[/math]

For proof, write this homogeneous polynomial as determinants and use Laplace expansion (in reverse).

[math]\displaystyle{ \begin{align} 0 & = \begin{vmatrix}x_0&y_0\\x_1&y_1\end{vmatrix}\begin{vmatrix}x_2&y_2\\x_3&y_3\end{vmatrix}+ \begin{vmatrix}x_0&y_0\\x_2&y_2\end{vmatrix}\begin{vmatrix}x_3&y_3\\x_1&y_1\end{vmatrix}+ \begin{vmatrix}x_0&y_0\\x_3&y_3\end{vmatrix}\begin{vmatrix}x_1&y_1\\x_2&y_2\end{vmatrix} \\[5pt] & = (x_0 y_1-y_0 x_1)\begin{vmatrix}x_2&y_2\\x_3&y_3\end{vmatrix}- (x_0 y_2-y_0 x_2)\begin{vmatrix}x_1&y_1\\x_3&y_3\end{vmatrix}+ (x_0 y_3-y_0 x_3)\begin{vmatrix}x_1&y_1\\x_2&y_2\end{vmatrix} \\[5pt] & = x_0 \left(y_1\begin{vmatrix}x_2&y_2\\x_3&y_3\end{vmatrix}- y_2\begin{vmatrix}x_1&y_1\\x_3&y_3\end{vmatrix}+ y_3\begin{vmatrix}x_1&y_1\\x_2&y_2\end{vmatrix}\right) -y_0 \left(x_1\begin{vmatrix}x_2&y_2\\x_3&y_3\end{vmatrix}- x_2\begin{vmatrix}x_1&y_1\\x_3&y_3\end{vmatrix}+ x_3\begin{vmatrix}x_1&y_1\\x_2&y_2\end{vmatrix}\right) \\[5pt] & = x_0 \begin{vmatrix}x_1&y_1&y_1\\x_2&y_2&y_2\\x_3&y_3&y_3\end{vmatrix} -y_0 \begin{vmatrix}x_1&x_1&y_1\\x_2&x_2&y_2\\x_3&x_3&y_3\end{vmatrix} \end{align} }[/math]

Since both 3×3 determinants have duplicate columns, the right hand side is identically zero.

Another proof may be done like this: Since vector

[math]\displaystyle{ d = \left( p_{01}, p_{02}, p_{03} \right) }[/math]

is perpendicular to vector

[math]\displaystyle{ m = \left( p_{23}, p_{31}, p_{12} \right) }[/math]

(see above), the scalar product of d and m must be zero. q.e.d.

Point equations

Letting (x₀ : x₁ : x₂ : x₃) be the point coordinates, four possible points on a line each have coordinates x_i = p_ij, for j = 0, 1, 2, 3. Some of these possible points may be inadmissible because all coordinates are zero, but since at least one Plücker coordinate is nonzero, at least two distinct points are guaranteed.

Bijectivity

If [math]\displaystyle{ (q_{01}:q_{02}:q_{03}:q_{23}:q_{31}:q_{12}) }[/math] are the homogeneous coordinates of a point in [math]\displaystyle{ \mathbb P^5 }[/math], without loss of generality assume that q₀₁ is nonzero. Then the matrix

[math]\displaystyle{ M = \begin{bmatrix} q_{01} & 0 \\ 0 & q_{01} \\ -q_{12} & q_{02} \\ q_{31} & q_{03} \end{bmatrix} }[/math]

has rank 2, and so its columns are distinct points defining a line L. When the [math]\displaystyle{ \mathbb P^5 }[/math] coordinates, q_ij, satisfy the quadratic Plücker relation, they are the Plücker coordinates of L. To see this, first normalize q₀₁ to 1. Then we immediately have that for the Plücker coordinates computed from M, p_ij = q_ij, except for

[math]\displaystyle{ p_{23} = - q_{03} q_{12} - q_{02} q_{31} . }[/math]

But if the q_ij satisfy the Plücker relation

[math]\displaystyle{ q_{23} + q_{02}q_{31} + q_{03}q_{12} = 0, }[/math]

then p₂₃ = q₂₃, completing the set of identities.

Consequently, α is a surjection onto the algebraic variety consisting of the set of zeros of the quadratic polynomial

[math]\displaystyle{ p_{01}p_{23}+p_{02}p_{31}+p_{03}p_{12} . }[/math]

And since α is also an injection, the lines in [math]\displaystyle{ \mathbb P^3 }[/math] are thus in bijective correspondence with the points of this quadric in [math]\displaystyle{ \mathbb P^5 }[/math], called the Plücker quadric or Klein quadric.

Uses

Plücker coordinates allow concise solutions to problems of line geometry in 3-dimensional space, especially those involving incidence.

Line-line crossing

Two lines in [math]\displaystyle{ \mathbb P^3 }[/math] are either skew or coplanar, and in the latter case they are either coincident or intersect in a unique point. If p_ij and p′_ij are the Plücker coordinates of two lines, then they are coplanar precisely when

[math]\displaystyle{ \mathbf d \cdot \mathbf m' + \mathbf m \cdot \mathbf d' = 0, }[/math]

as shown by

[math]\displaystyle{ \begin{align} 0 & = p_{01}p'_{23} + p_{02}p'_{31} + p_{03}p'_{12} + p_{23}p'_{01} + p_{31}p'_{02} + p_{12}p'_{03} \\[5pt] & = \begin{vmatrix}x_0&y_0&x'_0&y'_0\\ x_1&y_1&x'_1&y'_1\\ x_2&y_2&x'_2&y'_2\\ x_3&y_3&x'_3&y'_3\end{vmatrix}. \end{align} }[/math]

When the lines are skew, the sign of the result indicates the sense of crossing: positive if a right-handed screw takes L into L′, else negative.

The quadratic Plücker relation essentially states that a line is coplanar with itself.

Line-line join

In the event that two lines are coplanar but not parallel, their common plane has equation

[math]\displaystyle{ 0 = (\mathbf m \cdot \mathbf d')x_0 + (\mathbf d \times \mathbf d')\cdot \mathbf x, }[/math]

where [math]\displaystyle{ x=(x_1,x_2,x_3). }[/math]

The slightest perturbation will destroy the existence of a common plane, and near-parallelism of the lines will cause numeric difficulties in finding such a plane even if it does exist.

Line-line meet

Dually, two coplanar lines, neither of which contains the origin, have common point

[math]\displaystyle{ (x_0:\mathbf x) = (\mathbf d \cdot \mathbf m': \mathbf m \times \mathbf m'). }[/math]

To handle lines not meeting this restriction, see the references.

Plane-line meet

Given a plane with equation

[math]\displaystyle{ 0 = a^0x_0 + a^1x_1 + a^2x_2 + a^3x_3 , }[/math]

or more concisely,

[math]\displaystyle{ 0 = a^0x_0 + \mathbf a \cdot \mathbf x; }[/math]

and given a line not in it with Plücker coordinates (d : m), then their point of intersection is

[math]\displaystyle{ (x_0 : \mathbf x) = (\mathbf a \cdot \mathbf d : \mathbf a \times \mathbf m - a_0\mathbf d) . }[/math]

The point coordinates, (x₀ : x₁ : x₂ : x₃), can also be expressed in terms of Plücker coordinates as

[math]\displaystyle{ x_i = \sum_{j \ne i} a^j p_{ij} , \qquad i = 0 \ldots 3 . }[/math]

Point-line join

Dually, given a point (y₀ : y) and a line not containing it, their common plane has equation

[math]\displaystyle{ 0 = (\mathbf y \cdot \mathbf m) x_0 + (\mathbf y \times \mathbf d - y_0 \mathbf m)\cdot \mathbf x. }[/math]

The plane coordinates, (a⁰ : a¹ : a² : a³), can also be expressed in terms of dual Plücker coordinates as

[math]\displaystyle{ a^i = \sum_{j \ne i} y_j p^{ij} , \qquad i = 0 \ldots 3 . }[/math]

Line families

Because the Klein quadric is in [math]\displaystyle{ \mathbb P^5 }[/math], it contains linear subspaces of dimensions one and two (but no higher). These correspond to one- and two-parameter families of lines in [math]\displaystyle{ \mathbb P^3 }[/math].

For example, suppose L, L′ are distinct lines in [math]\displaystyle{ \mathbb P^3 }[/math] determined by points x, y and x′, y′, respectively. Linear combinations of their determining points give linear combinations of their Plücker coordinates, generating a one-parameter family of lines containing L and L′. This corresponds to a one-dimensional linear subspace belonging to the Klein quadric.

Lines in plane

If three distinct and non-parallel lines are coplanar; their linear combinations generate a two-parameter family of lines, all the lines in the plane. This corresponds to a two-dimensional linear subspace belonging to the Klein quadric.

Lines through point

If three distinct and non-coplanar lines intersect in a point, their linear combinations generate a two-parameter family of lines, all the lines through the point. This also corresponds to a two-dimensional linear subspace belonging to the Klein quadric.

Ruled surface

A ruled surface is a family of lines that is not necessarily linear. It corresponds to a curve on the Klein quadric. For example, a hyperboloid of one sheet is a quadric surface in [math]\displaystyle{ \mathbb P^3 }[/math] ruled by two different families of lines, one line of each passing through each point of the surface; each family corresponds under the Plücker map to a conic section within the Klein quadric in [math]\displaystyle{ \mathbb P^5 }[/math].

Line geometry

During the nineteenth century, line geometry was studied intensively. In terms of the bijection given above, this is a description of the intrinsic geometry of the Klein quadric.

Ray tracing

Line geometry is extensively used in ray tracing application where the geometry and intersections of rays need to be calculated in 3D. An implementation is described in Introduction to Plücker Coordinates written for the Ray Tracing forum by Thouis Jones.

See also

• Flat projective plane
• Plücker matrix

References

• Hodge, W. V. D.; D. Pedoe (1994). Methods of Algebraic Geometry, Volume I (Book II). Cambridge University Press. ISBN 978-0-521-46900-5. 
• Behnke, H., ed (1984). Fundamentals of Mathematics, Volume II: Geometry. trans. S. H. Gould. MIT Press. ISBN 978-0-262-52094-2. 
  From the German: Grundzüge der Mathematik, Band II: Geometrie. Vandenhoeck & Ruprecht.
• Guilfoyle, B.; W. Klingenberg (2004). "On the space of oriented affine lines in R^3". Archiv der Mathematik (Birkhäuser) 82 (1): 81–84. doi:10.1007/s00013-003-4861-3. ISSN 0003-889X. 
• Hazewinkel, Michiel, ed. (2001), "Plücker coordinates", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4, https://www.encyclopediaofmath.org/index.php?title=Main_Page 
• Mason, Matthew T.; J. Kenneth Salisbury (1985). Robot Hands and the Mechanics of Manipulation. MIT Press. ISBN 978-0-262-13205-3. 
• Hartley, R.~I.; Zisserman A. (2004). Multiple View Geometry in Computer Vision. Cambridge University Press. ISBN 0521540518. http://www.robots.ox.ac.uk/~vgg/hzbook/. 
• Hohmeyer, M.; S. Teller (1999). "Determining the Lines Through Four Lines". Journal of Graphics Tools (A K Peters) 4 (3): 11–22. doi:10.1080/10867651.1999.10487506. ISSN 1086-7651. http://people.csail.mit.edu/seth/pubs/TellerHohmeyerJGT2000.pdf. 
• Shafarevich, I. R.; A. O. Remizov (2012). Linear Algebra and Geometry. Springer. ISBN 978-3-642-30993-9. https://www.springer.com/mathematics/algebra/book/978-3-642-30993-9. 
• Jia, Yan-Bin (2017). Plücker Coordinates for Lines in the Space (Report). http://web.cs.iastate.edu/~cs577/handouts/plucker-coordinates.pdf. 
• Shoemake, Ken (1998). "Plücker Coordinate Tutorial". Ray Tracing News. http://www.realtimerendering.com/resources/RTNews/html/rtnv11n1.html#art3.