Euclidean tilings by convex regular polygons

Short description: Subdivision of the plane into polygons that are all regular

Example periodic tilings

A regular tiling has one type of regular face.	A semiregular or uniform tiling has one type of vertex, but two or more types of faces.
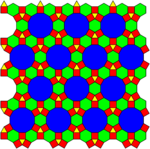A k-uniform tiling has k types of vertices, and two or more types of regular faces.	A non-edge-to-edge tiling can have different-sized regular faces.

Euclidean plane tilings by convex regular polygons have been widely used since antiquity. The first systematic mathematical treatment was that of Kepler in his Harmonices Mundi (Latin: The Harmony of the World, 1619).

Notation of Euclidean tilings

Euclidean tilings are usually named after Cundy & Rollett’s notation. This notation represents (i) the number of vertices, (ii) the number of polygons around each vertex (arranged clockwise) and (iii) the number of sides to each of those polygons. For example: 3⁶; 3⁶; 3⁴.6, tells us there are 3 vertices with 2 different vertex types, so this tiling would be classed as a ‘3-uniform (2-vertex types)’ tiling. Broken down, 3⁶; 3⁶ (both of different transitivity class), or (3⁶)², tells us that there are 2 vertices (denoted by the superscript 2), each with 6 equilateral 3-sided polygons (triangles). With a final vertex 3⁴.6, 4 more contiguous equilateral triangles and a single regular hexagon.

However, this notation has two main problems related to ambiguous conformation and uniqueness First, when it comes to k-uniform tilings, the notation does not explain the relationships between the vertices. This makes it impossible to generate a covered plane given the notation alone. And second, some tessellations have the same nomenclature, they are very similar but it can be noticed that the relative positions of the hexagons are different. Therefore, the second problem is that this nomenclature is not unique for each tessellation.

In order to solve those problems, GomJau-Hogg’s notation is a slightly modified version of the research and notation presented in 2012, about the generation and nomenclature of tessellations and double-layer grids. Antwerp v3.0, a free online application, allows for the infinite generation of regular polygon tilings through a set of shape placement stages and iterative rotation and reflection operations, obtained directly from the GomJau-Hogg’s notation.

Regular tilings

Following Grünbaum and Shephard (section 1.3), a tiling is said to be regular if the symmetry group of the tiling acts transitively on the flags of the tiling, where a flag is a triple consisting of a mutually incident vertex, edge and tile of the tiling. This means that, for every pair of flags, there is a symmetry operation mapping the first flag to the second. This is equivalent to the tiling being an edge-to-edge tiling by congruent regular polygons. There must be six equilateral triangles, four squares or three regular hexagons at a vertex, yielding the three regular tessellations.

Regular tilings (3)

p6m, *632		p4m, *442
C&R: 36 GJ-H: 3/m30/r(h2) (t = 1, e = 1)	C&R: 63 GJ-H: 6/m30/r(h1) (t = 1, e = 1)	C&R: 44 GJ-H: 4/m45/r(h1) (t = 1, e = 1)

C&R: Cundy & Rollet's notation
GJ-H: Notation of GomJau-Hogg

Archimedean, uniform or semiregular tilings

Further information: List of convex uniform tilings

Vertex-transitivity means that for every pair of vertices there is a symmetry operation mapping the first vertex to the second.

If the requirement of flag-transitivity is relaxed to one of vertex-transitivity, while the condition that the tiling is edge-to-edge is kept, there are eight additional tilings possible, known as Archimedean, uniform or semiregular tilings. Note that there are two mirror image (enantiomorphic or chiral) forms of 3⁴.6 (snub hexagonal) tiling, only one of which is shown in the following table. All other regular and semiregular tilings are achiral.

Uniform tilings (8)

p6m, *632
150x150px|alt= C&R: 3.122 GJ-H: 12-3/m30/r(h3) (t = 2, e = 2) t{6,3}	100x100px|alt= C&R: 3.4.6.4 GJ-H: 6-4-3/m30/r(c2) (t = 3, e = 2) rr{3,6}	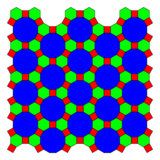150x150px|alt= C&R: 4.6.12 GJ-H: 12-6,4/m30/r(c2) (t = 3, e = 3) tr{3,6}	150x150px|alt= C&R: (3.6)2 GJ-H: 6-3-6/m30/r(v4) (t = 2, e = 1) r{6,3}
150x150px|alt= C&R: 4.82 GJ-H: 8-4/m90/r(h4) (t = 2, e = 2) t{4,4}	150x150px|alt= C&R: 32.4.3.4 GJ-H: 4-3-3,4/r90/r(h2) (t = 2, e = 2) s{4,4}	150x150px|alt= C&R: 33.42 GJ-H: 4-3/m90/r(h2) (t = 2, e = 3) {3,6}:e	C&R: 34.6 GJ-H: 6-3-3/r60/r(h5) (t = 3, e = 3) sr{3,6}

C&R: Cundy & Rollet's notation
GJ-H: Notation of GomJau-Hogg

Grünbaum and Shephard distinguish the description of these tilings as Archimedean as referring only to the local property of the arrangement of tiles around each vertex being the same, and that as uniform as referring to the global property of vertex-transitivity. Though these yield the same set of tilings in the plane, in other spaces there are Archimedean tilings which are not uniform.

Plane-vertex tilings

There are 17 combinations of regular convex polygons that form 21 types of plane-vertex tilings. Polygons in these meet at a point with no gap or overlap. Listing by their vertex figures, one has 6 polygons, three have 5 polygons, seven have 4 polygons, and ten have 3 polygons.

As detailed in the sections above, three of them can make regular tilings (6³, 4⁴, 3⁶), and eight more can make semiregular or archimedean tilings, (3.12.12, 4.6.12, 4.8.8, (3.6)², 3.4.6.4, 3.3.4.3.4, 3.3.3.4.4, 3.3.3.3.6). Four of them can exist in higher k-uniform tilings (3.3.4.12, 3.4.3.12, 3.3.6.6, 3.4.4.6), while six can not be used to completely tile the plane by regular polygons with no gaps or overlaps - they only tessellate space entirely when irregular polygons are included (3.7.42, 3.8.24, 3.9.18, 3.10.15, 4.5.20, 5.5.10).

The plane-vertex tilings

6	36
5	3.3.4.3.4	3.3.3.4.4	3.3.3.3.6
4	3.3.4.12	3.4.3.12	3.3.6.6	(3.6)2	3.4.4.6	3.4.6.4	44
3	3.7.42	3.8.24	3.9.18	3.10.15	3.12.12	4.5.20	4.6.12	4.8.8	5.5.10	63

k-uniform tilings

Such periodic tilings may be classified by the number of orbits of vertices, edges and tiles. If there are k orbits of vertices, a tiling is known as k-uniform or k-isogonal; if there are t orbits of tiles, as t-isohedral; if there are e orbits of edges, as e-isotoxal.

k-uniform tilings with the same vertex figures can be further identified by their wallpaper group symmetry.

1-uniform tilings include 3 regular tilings, and 8 semiregular ones, with 2 or more types of regular polygon faces. There are 20 2-uniform tilings, 61 3-uniform tilings, 151 4-uniform tilings, 332 5-uniform tilings and 673 6-uniform tilings. Each can be grouped by the number m of distinct vertex figures, which are also called m-Archimedean tilings.

Finally, if the number of types of vertices is the same as the uniformity (m = k below), then the tiling is said to be Krotenheerdt. In general, the uniformity is greater than or equal to the number of types of vertices (m ≥ k), as different types of vertices necessarily have different orbits, but not vice versa. Setting m = n = k, there are 11 such tilings for n = 1; 20 such tilings for n = 2; 39 such tilings for n = 3; 33 such tilings for n = 4; 15 such tilings for n = 5; 10 such tilings for n = 6; and 7 such tilings for n = 7.

Below is an example of a 3-unifom tiling:

Colored 3-uniform tiling #57 of 61

by sides, yellow triangles, red squares (by polygons)

by 4-isohedral positions, 3 shaded colors of triangles (by orbits)

k-uniform, m-Archimedean tiling counts

		m-Archimedean
		1	2	3	4	5	6	7	8	9	10	11	12	13	14	≥ 15	Total
k-uniform	1	11	0	0	0	0	0	0	0	0	0	0	0	0	0	0	11
	2	0	20	0	0	0	0	0	0	0	0	0	0	0	0	0	20
	3	0	22	39	0	0	0	0	0	0	0	0	0	0	0	0	61
	4	0	33	85	33	0	0	0	0	0	0	0	0	0	0	0	151
	5	0	74	149	94	15	0	0	0	0	0	0	0	0	0	0	332
	6	0	100	284	187	92	10	0	0	0	0	0	0	0	0	0	673
	7	0	?	?	?	?	?	7	0	0	0	0	0	0	0	0	1472
	8	0	?	?	?	?	?	20	0	0	0	0	0	0	0	0	2850
	9	0	?	?	?	?	?	?	8	0	0	0	0	0	0	0	5960
	10	0	?	?	?	?	?	?	27	0	0	0	0	0	0	0	11866
	11	0	?	?	?	?	?	?	?	1	0	0	0	0	0	0	24459
	12	0	?	?	?	?	?	?	?	?	0	0	0	0	0	0	49794
	13	0	?	?	?	?	?	?	?	?	?	?	?	0	0	0	103082
	14	0	?	?	?	?	?	?	?	?	?	?	?	?	0	0	?
	≥ 15	0	?	?	?	?	?	?	?	?	?	?	?	?	?	0	?
	Total	11	∞	∞	∞	∞	∞	∞	∞	∞	∞	∞	∞	∞	∞	0	∞

2-uniform tilings

There are twenty (20) 2-uniform tilings of the Euclidean plane. (also called 2-isogonal tilings or demiregular tilings) Vertex types are listed for each. If two tilings share the same two vertex types, they are given subscripts 1,2.

2-uniform tilings (20)

p6m, *632						p4m, *442
[36; 32.4.3.4] 3-4-3/m30/r(c3) (t = 3, e = 3)	[3.4.6.4; 32.4.3.4] 6-4-3,3/m30/r(h1) (t = 4, e = 4)	[3.4.6.4; 33.42] 6-4-3-3/m30/r(h5) (t = 4, e = 4)	[3.4.6.4; 3.42.6] 6-4-3,4-6/m30/r(c4) (t = 5, e = 5)	[4.6.12; 3.4.6.4] 12-4,6-3/m30/r(c3) (t = 4, e = 4)	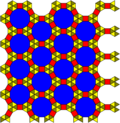[36; 32.4.12] 12-3,4-3/m30/r(c3) (t = 4, e = 4)	[3.12.12; 3.4.3.12] 12-0,3,3-0,4/m45/m(h1) (t = 3, e = 3)
p6m, *632	p6, 632	p6, 632	cmm, 2*22	pmm, *2222	cmm, 2*22	pmm, *2222
[36; 32.62] 3-6/m30/r(c2) (t = 2, e = 3)	[36; 34.6]1 6-3,3-3/m30/r(h1) (t = 3, e = 3)	[36; 34.6]2 6-3-3,3-3/r60/r(h8) (t = 5, e = 7)	[32.62; 34.6] 6-3/m90/r(h1) (t = 2, e = 4)	[3.6.3.6; 32.62] 6-3,6/m90/r(h3) (t = 2, e = 3)	[3.42.6; 3.6.3.6]2 6-3,4-6-3,4-6,4/m90/r(c6) (t = 3, e = 4)	[3.42.6; 3.6.3.6]1 6-3,4/m90/r(h4) (t = 4, e = 4)
p4g, 4*2	pgg, 22×	cmm, 2*22	cmm, 2*22	pmm, *2222	cmm, 2*22
[33.42; 32.4.3.4]1 4-3,3-4,3/r90/m(h3) (t = 4, e = 5)	[33.42; 32.4.3.4]2 4-3,3,3-4,3/r(c2)/r(h13)/r(h45) (t = 3, e = 6)	[44; 33.42]1 4-3/m(h4)/m(h3)/r(h2) (t = 2, e = 4)	[44; 33.42]2 4-4-3-3/m90/r(h3) (t = 3, e = 5)	[36; 33.42]1 4-3,4-3,3/m90/r(h3) (t = 3, e = 4)	[36; 33.42]2 4-3-3-3/m90/r(h7)/r(h5) (t = 4, e = 5)

Higher k-uniform tilings

k-uniform tilings have been enumerated up to 6. There are 673 6-uniform tilings of the Euclidean plane. Brian Galebach's search reproduced Krotenheerdt's list of 10 6-uniform tilings with 6 distinct vertex types, as well as finding 92 of them with 5 vertex types, 187 of them with 4 vertex types, 284 of them with 3 vertex types, and 100 with 2 vertex types.

Fractalizing k-uniform tilings

There are many ways of generating new k-uniform tilings from old k-uniform tilings. For example, notice that the 2-uniform [3.12.12; 3.4.3.12] tiling has a square lattice, the 4(3-1)-uniform [343.12; (3.12²)3] tiling has a snub square lattice, and the 5(3-1-1)-uniform [334.12; 343.12; (3.12.12)3] tiling has an elongated triangular lattice. These higher-order uniform tilings use the same lattice but possess greater complexity. The fractalizing basis for theses tilings is as follows:

	Triangle	Square	Hexagon	Dissected Dodecagon
Shape
Fractalizing

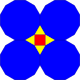The side lengths are dilated by a factor of [math]\displaystyle{ 2+\sqrt{3} }[/math].

This can similarly be done with the truncated trihexagonal tiling as a basis, with corresponding dilation of [math]\displaystyle{ 3+\sqrt{3} }[/math].

	Triangle	Square	Hexagon	Dissected Dodecagon
Shape
Fractalizing

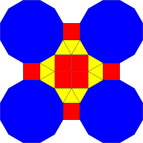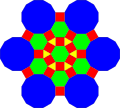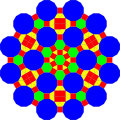Fractalizing examples

	Truncated Hexagonal Tiling	Truncated Trihexagonal Tiling
Fractalizing

Tilings that are not edge-to-edge

Convex regular polygons can also form plane tilings that are not edge-to-edge. Such tilings can be considered edge-to-edge as nonregular polygons with adjacent colinear edges.

There are seven families of isogonal each family having a real-valued parameter determining the overlap between sides of adjacent tiles or the ratio between the edge lengths of different tiles. Two of the families are generated from shifted square, either progressive or zig-zagging positions. Grünbaum and Shephard call these tilings uniform although it contradicts Coxeter's definition for uniformity which requires edge-to-edge regular polygons. Such isogonal tilings are actually topologically identical to the uniform tilings, with different geometric proportions.

Periodic isogonal tilings by non-edge-to-edge convex regular polygons

1	2	3	4	5	6	7
Rows of squares with horizontal offsets		Rows of triangles with horizontal offsets	A tiling by squares	Three hexagons surround each triangle	Six triangles surround every hexagon.	Three size triangles
cmm (2*22)	p2 (2222)	cmm (2*22)	p4m (*442)	p6 (632)		p3 (333)
Hexagonal tiling		Square tiling	Truncated square tiling	Truncated hexagonal tiling	Hexagonal tiling	Trihexagonal tiling

See also

• Grid (spatial index)
• Uniform tilings in hyperbolic plane
• List of uniform tilings
• Wythoff symbol
• Tessellation
• Wallpaper group
• Regular polyhedron (the Platonic solids)
• Semiregular polyhedron (including the Archimedean solids)
• Hyperbolic geometry
• Penrose tiling
• Tiling with rectangles
• Lattice (group)

References

• Grünbaum, Branko; Shephard, Geoffrey C. (1977). "Tilings by regular polygons". Math. Mag. 50 (5): 227–247. doi:10.2307/2689529. 
• Grünbaum, Branko; Shephard, G. C. (1978). "The ninety-one types of isogonal tilings in the plane". Trans. Am. Math. Soc. 252: 335–353. doi:10.1090/S0002-9947-1978-0496813-3. 
• Debroey, I.; Landuyt, F. (1981). "Equitransitive edge-to-edge tilings". Geometriae Dedicata 11 (1): 47–60. doi:10.1007/BF00183189. 
• Grünbaum, Branko; Shephard, G. C. (1987). Tilings and Patterns. W. H. Freeman and Company. ISBN 0-7167-1193-1. https://archive.org/details/isbn_0716711931. 
• Ren, Ding; Reay, John R. (1987). "The boundary characteristic and Pick's theorem in the Archimedean planar tilings". J. Comb. Theory A 44 (1): 110–119. doi:10.1016/0097-3165(87)90063-X. 
• Chavey, D. (1989). "Tilings by Regular Polygons—II: A Catalog of Tilings". Computers & Mathematics with Applications 17: 147–165. doi:10.1016/0898-1221(89)90156-9. https://www.beloit.edu/computerscience/faculty/chavey/catalog/. 
• Order in Space: A design source book, Keith Critchlow, 1970 ISBN:978-0-670-52830-1
• Sommerville, Duncan MacLaren Young (1958). An Introduction to the Geometry of n Dimensions. Dover Publications.  Chapter X: The Regular Polytopes
• Préa, P. (1997). "Distance sequences and percolation thresholds in Archimedean Tilings". Mathl. Comput. Modelling 26 (8–10): 317–320. doi:10.1016/S0895-7177(97)00216-1. 
• Kovic, Jurij (2011). "Symmetry-type graphs of Platonic and Archimedean solids". Math. Commun. 16 (2): 491–507. http://hrcak.srce.hr/74895. 
• Pellicer, Daniel; Williams, Gordon (2012). "Minimal Covers of the Archimedean Tilings, Part 1". The Electronic Journal of Combinatorics 19 (3): #P6. doi:10.37236/2512. http://www.combinatorics.org/ojs/index.php/eljc/article/view/v19i3p6. 
• Dale Seymour and Jill Britton, Introduction to Tessellations, 1989, ISBN:978-0866514613, pp. 50–57

External links

Euclidean and general tiling links:

• n-uniform tilings, Brian Galebach
• Dutch, Steve. "Uniform Tilings". http://www.uwgb.edu/dutchs/symmetry/uniftil.htm. 
• Mitchell, K. "Semi-Regular Tilings". http://people.hws.edu/mitchell/tilings/Part1.html. 
• Weisstein, Eric W.. "Tessellation". http://mathworld.wolfram.com/Tessellation.html. 
• Weisstein, Eric W.. "Semiregular tessellation". http://mathworld.wolfram.com/SemiregularTessellation.html. 
• Weisstein, Eric W.. "Demiregular tessellation". http://mathworld.wolfram.com/DemiregularTessellation.html.