Reversible cellular automaton
A reversible cellular automaton is a cellular automaton in which every configuration has a unique predecessor. That is, it is a regular grid of cells, each containing a state drawn from a finite set of states, with a rule for updating all cells simultaneously based on the states of their neighbors, such that the previous state of any cell before an update can be determined uniquely from the updated states of all the cells. The time-reversed dynamics of a reversible cellular automaton can always be described by another cellular automaton rule, possibly on a much larger neighborhood.
Several methods are known for defining cellular automata rules that are reversible; these include the block cellular automaton method, in which each update partitions the cells into blocks and applies an invertible function separately to each block, and the second-order cellular automaton method, in which the update rule combines states from two previous steps of the automaton. When an automaton is not defined by one of these methods, but is instead given as a rule table, the problem of testing whether it is reversible is solvable for block cellular automata and for one-dimensional cellular automata, but is undecidable for other types of cellular automata.
Reversible cellular automata form a natural model of reversible computing, a technology that could lead to ultra-low-power computing devices. Quantum cellular automata, one way of performing computations using the principles of quantum mechanics, are often required to be reversible. Additionally, many problems in physical modeling, such as the motion of particles in an ideal gas or the Ising model of alignment of magnetic charges, are naturally reversible and can be simulated by reversible cellular automata.
Properties related to reversibility may also be used to study cellular automata that are not reversible on their entire configuration space, but that have a subset of the configuration space as an attractor that all initially random configurations converge towards. As Stephen Wolfram writes, "once on an attractor, any system—even if it does not have reversible underlying rules—must in some sense show approximate reversibility."[1]
Examples
One-dimensional automata
A cellular automaton is defined by its cells (often a one- or two-dimensional array), a finite set of values or states that can go into each cell, a neighborhood associating each cell with a finite set of nearby cells, and an update rule according to which the values of all cells are updated, simultaneously, as a function of the values of their neighboring cells. The simplest possible cellular automata have a one-dimensional array of cells, each of which can hold a binary value (either 0 or 1), with each cell having a neighborhood consisting only of it and its two nearest cells on either side; these are called the elementary cellular automata.[2] If the update rule for such an automaton causes each cell to always remain in the same state, then the automaton is reversible: the previous state of all cells can be recovered from their current states, because for each cell the previous and current states are the same. Similarly, if the update rule causes every cell to change its state from 0 to 1 and vice versa, or if it causes a cell to copy the state from a fixed neighboring cell, or if it causes it to copy a state and then reverse its value, it is necessarily reversible.[3] (Toffoli Margolus) call these types of reversible cellular automata, in which the state of each cell depends only on the previous state of one neighboring cell, "trivial". Despite its simplicity, the update rule that causes each cell to copy the state of a neighboring cell is important in the theory of symbolic dynamics, where it is known as the shift map.[4]
A little less trivially, suppose that the cells again form a one-dimensional array, but that each state is an ordered pair (l,r) consisting of a left part l and a right part r, each drawn from a finite set of possible values. Define a transition function that sets the left part of a cell to be the left part of its left neighbor and the right part of a cell to be the right part of its right neighbor. That is, if the left neighbor's state is (a,b) and the right neighbor's state is (c,d), the new state of a cell is the result of combining these states using a pairwise operation × defined by the equation (a,b) × (c,d) = (a,d). An example of this construction is given in the illustration, in which the left part is represented graphically as a shape and the right part is represented as a color; in this example, each cell is updated with the shape of its left neighbor and the color of its right neighbor. Then this automaton is reversible: the values on the left side of each pair migrate rightwards and the values on the right side migrate leftwards, so the prior state of each cell can be recovered by looking for these values in neighboring cells. The operation × used to combine pairs of states in this automaton forms an algebraic structure known as a rectangular band.[5]
Multiplication of decimal numbers by two or by five can be performed by a one-dimensional reversible cellular automaton with ten states per cell (the ten decimal digits). Each digit of the product depends only on a neighborhood of two digits in the given number: the digit in the same position and the digit one position to the right. More generally, multiplication or division of doubly infinite digit sequences in any radix b, by a multiplier or divisor x all of whose prime factors are also prime factors of b, is an operation that forms a cellular automaton because it depends only on a bounded number of nearby digits, and is reversible because of the existence of multiplicative inverses.[6] Multiplication by other values (for instance, multiplication of decimal numbers by three) remains reversible, but does not define a cellular automaton, because there is no fixed bound on the number of digits in the initial value that are needed to determine a single digit in the result.
There are no nontrivial reversible elementary cellular automata.[7] However, a near-miss is provided by Rule 90 and other elementary cellular automata based on the exclusive or function. In Rule 90, the state of each cell is the exclusive or of the previous states of its two neighbors. This use of the exclusive or makes the transition rule locally invertible, in the sense that any contiguous subsequence of states can be generated by this rule. Rule 90 is not a reversible cellular automaton rule, because in Rule 90 every assignment of states to the complete array of cells has exactly four possible predecessors, whereas reversible rules are required to have exactly one predecessor per configuration.[8]
Critters' rule

Conway's Game of Life, one of the most famous cellular automaton rules, is not reversible: for instance, it has many patterns that die out completely, so the configuration in which all cells are dead has many predecessors, and it also has Garden of Eden patterns with no predecessors. However, another rule called "Critters" by its inventors, Tommaso Toffoli and Norman Margolus, is reversible and has similar dynamic behavior to Life.[9]
The Critters rule is a block cellular automaton in which, at each step, the cells of the automaton are partitioned into 2×2 blocks and each block is updated independently of the other blocks. Its transition function flips the state of every cell in a block that does not have exactly two live cells, and in addition rotates by 180° blocks with exactly three live cells. Because this function is invertible, the automaton defined by these rules is a reversible cellular automaton.[9]
When started with a smaller field of random cells centered within a larger region of dead cells, many small patterns similar to Life's glider escape from the central random area and interact with each other. The Critters rule can also support more complex spaceships of varying speeds as well as oscillators with infinitely many different periods.[9]
Constructions
Several general methods are known for constructing cellular automaton rules that are automatically reversible.
Block cellular automata
A block cellular automaton is an automaton at which, in each time step, the cells of the automaton are partitioned into congruent subsets (called blocks), and the same transformation is applied independently to each block. Typically, such an automaton will use more than one partition into blocks, and will rotate between these partitions at different time steps of the system.[10] In a frequently used form of this design, called the Margolus neighborhood, the cells of the automaton form a square grid and are partitioned into larger 2 × 2 square blocks at each step. The center of a block at one time step becomes the corner of four blocks at the next time step, and vice versa; in this way, the four cells in each 2 × 2 belong to four different 2 × 2 squares of the previous partition.[11] The Critters rule discussed above is an example of this type of automaton.
Designing reversible rules for block cellular automata, and determining whether a given rule is reversible, is easy: for a block cellular automaton to be reversible it is necessary and sufficient that the transformation applied to the individual blocks at each step of the automaton is itself reversible. When a block cellular automaton is reversible, the time-reversed version of its dynamics can also be described as a block cellular automaton with the same block structure, using a time-reversed sequence of partitions of cells into blocks, and with the transition function for each block being the inverse function of the original rule.[10]
Simulation of irreversible automata
(Toffoli 1977) showed how to embed any irreversible d-dimensional cellular automaton rule into a reversible (d + 1)-dimensional rule. Each d-dimensional slice of the new reversible rule simulates a single time step of the original rule. In this way, Toffoli showed that many features of irreversible cellular automata, such as the ability to simulate arbitrary Turing machines, could also be extended to reversible cellular automata.
As Toffoli conjectured and (Hertling 1998) proved, the increase in dimension incurred by Toffoli's method is a necessary payment for its generality: under mild assumptions (such as the translation-invariance of the embedding), any embedding of a cellular automaton that has a Garden of Eden into a reversible cellular automaton must increase the dimension.
(Morita 1995) describes another type of simulation that does not obey Hertling's assumptions and does not change the dimension. Morita's method can simulate the finite configurations of any irreversible automaton in which there is a "quiescent" or "dead" state, such that if a cell and all its neighbors are quiescent then the cell remains quiescent in the next step. The simulation uses a reversible block cellular automaton of the same dimension as the original irreversible automaton. The information that would be destroyed by the irreversible steps of the simulated automaton is instead sent away from the configuration into the infinite quiescent region of the simulating automaton. This simulation does not update all cells of the simulated automaton simultaneously; rather, the time to simulate a single step is proportional to the size of the configuration being simulated. Nevertheless, the simulation accurately preserves the behavior of the simulated automaton, as if all of its cells were being updated simultaneously. Using this method it is possible to show that even one-dimensional reversible cellular automata are capable of universal computation.[12]
Second-order cellular automata
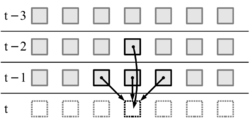
The second-order cellular automaton technique is a method of transforming any cellular automaton into a reversible cellular automaton, invented by Edward Fredkin and first published by several other authors in 1984.[13] In this technique, the state of each cell in the automaton at time t is a function both of its neighborhood at time t − 1 and of its own state at time t − 2. Specifically, the transition function of the automaton maps each neighborhood at time t − 1 to a permutation on the set of states, and then applies that permutation to the state at time t − 2. The reverse dynamics of the automaton may be computed by mapping each neighborhood to the inverse permutation and proceeding in the same way.[14]
In the case of automata with binary-valued states (zero or one), there are only two possible permutations on the states (the identity permutation and the permutation that swaps the two states), which may themselves be represented as the exclusive or of a state with a binary value. In this way, any conventional two-valued cellular automaton may be converted to a second-order cellular automaton rule by using the conventional automaton's transition function on the states at time t − 1, and then computing the exclusive or of these states with the states at time t − 2 to determine the states at time t. However, the behavior of the reversible cellular automaton determined in this way may not bear any resemblance to the behavior of the cellular automaton from which it was defined.[14]
Any second-order automaton may be transformed into a conventional cellular automaton, in which the transition function depends only on the single previous time step, by combining pairs of states from consecutive time steps of the second-order automaton into single states of a conventional cellular automaton.[14]
Conserved landscape
A one-dimensional cellular automaton found by (Patt 1971) uses a neighborhood consisting of four contiguous cells. In this automaton, a cell flips its state whenever it occupies the "?" position in the pattern "0?10". No two such patterns can overlap, so the same "landscape" surrounding the flipped cell continues to be present after the transition. In the next step, the cell in the same "?" position will flip again, back to its original state. Therefore, this automaton is its own inverse, and is reversible. Patt performed a brute force search of all two-state one-dimensional cellular automata with small neighborhoods; this search led to the discovery of this automaton, and showed that it was the simplest possible nontrivial one-dimensional two-state reversible cellular automaton. There are no nontrivial reversible two-state automata with three-cell neighborhoods, and all two-state reversible automata with four-cell neighborhoods are simple variants on Patt's automaton.[15]
Patt's automaton can be viewed in retrospect as an instance of the "conserved landscape" technique for designing reversible cellular automata. In this technique, a change to the state of a cell is triggered by a pattern among a set of neighbors that do not themselves change states. In this way, the existence of the same pattern can be used to trigger the inverse change in the time-reversed dynamics of the automaton. Patt's automaton has very simple dynamics (all cyclic sequences of configurations have length two), but automata using the same conserved landscape technique with more than one triggering pattern are capable of more complex behavior. In particular they can simulate any second-order cellular automaton.[15]
The SALT model of (Miller Fredkin) is a special case of the conserved landscape technique. In this model, the cells of an integer grid are split into even and odd subsets. In each time step certain pairs of cells of one parity are swapped, based on the configuration of nearby cells of the other parity. Rules using this model can simulate the billiard ball computer,[16] or support long strings of live cells that can move at many different speeds or vibrate at many different frequencies.[17]
Theory
A cellular automaton consists of an array of cells, each one of which has a finite number of possible states, together with a rule for updating all cells simultaneously based only on the states of neighboring cells. A configuration of a cellular automaton is an assignment of a state to every cell of the automaton; the update rule of a cellular automaton forms a function from configurations to configurations, with the requirement that the updated value of any cell depends only on some finite neighborhood of the cell, and that the function is invariant under translations of the input array.
With these definitions, a cellular automaton is reversible when it satisfies any one of the following conditions, all of which are mathematically equivalent to each other:[18]
- Every configuration of the automaton has a unique predecessor that is mapped to it by the update rule.
- The update rule of the automaton is a bijection; that is, a function that is both one-to-one and onto.
- The update rule is an injective function, that is, there are no two configurations that both map to the same common configuration. This condition is obviously implied by the assumption that the update rule is a bijection. In the other direction, the Garden of Eden theorem for cellular automata implies that every injective update rule is bijective.[19]
- The time-reversed dynamics of the automaton can be described by another cellular automaton. Clearly, for this to be possible, the update rule must be bijective. In the other direction, if the update rule is bijective, then it has an inverse function that is also bijective. This inverse function must be a cellular automaton rule. The proof of this fact uses the Curtis–Hedlund–Lyndon theorem, a topological characterization of cellular automata rules as the translation-invariant functions that are continuous with respect to the Cantor topology on the space of configurations.[20]
- The update rule of the automaton is an automorphism of the shift dynamical system defined by the state space and the translations of the lattice of cells. That is, it is a homeomorphism that commutes with the shift map, as the Curtis–Hedlund–Lyndon theorem implies.[21]
(Di Gregorio Trautteur) analyze several alternative definitions of reversibility for cellular automata. Most of these turn out to be equivalent either to injectivity or to surjectivity of the transition function of the automaton; however, there is one more alternative that does not match either of these two definitions. It applies to automata such as the Game of Life that have a quiescent or dead state. In such an automaton, one can define a configuration to be "finite" if it has only finitely many non-quiescent cells, and one can consider the class of automata for which every finite configuration has at least one finite predecessor. This class turns out to be distinct from both the surjective and injective automata, and in some subsequent research, automata with this property have been called invertible finite automata.[22]
Testing reversibility
It was first shown by (Amoroso Patt) that the problem of testing reversibility of a given one-dimensional cellular automaton has an algorithmic solution. Alternative algorithms based on automata theory and de Bruijn graphs were given by (Culik 1987) and (Sutner 1991), respectively.
- Culik begins with the observation that a cellular automaton has an injective transition function if and only if the transition function is injective on the subsets of configurations that are periodic (repeating the same substring infinitely often in both directions). He defines a nondeterministic finite-state transducer that performs the transition rule of the automaton on periodic strings. This transducer works by remembering the neighborhood of the automaton at the start of the string and entering an accepting state when that neighborhood concatenated to the end of the input would cause its nondeterministically chosen transitions to be correct. Culik then swaps the input and output of the transducer. The transducer resulting from this swap simulates the inverse dynamics of the given automaton. Finally, Culik applies previously known algorithms to test whether the resulting swapped transducer maps each input to a single output.[23]
- Sutner defines a directed graph (a type of de Bruijn graph) in which each vertex represents a pair of assignments of states for the cells in a contiguous sequence of cells. The length of this sequence is chosen to be one less than the neighborhood size of the automaton. An edge in Sutner's graph represents a pair of sequences of cells that overlap in all but one cell, so that the union of the sequences is a full neighborhood in the cellular automaton. Each such edge is directed from the overlapping subsequence on the left to the subsequence on the right. Edges are only included in the graph when they represent compatible state assignments on the overlapping parts of their cell sequences, and when the automaton rule (applied to the neighborhood determined by the potential edge) would give the same results for both assignments of states. By performing a linear-time strong connectivity analysis of this graph, it is possible to determine which of its vertices belong to cycles. The transition rule is non-injective if and only if this graph contains a directed cycle in which at least one vertex has two differing state assignments.[8]
These methods take polynomial time, proportional to the square of the size of the state transition table of the input automaton.[24] A related algorithm of (Hillman 1991) determines whether a given rule is surjective when applied to finite-length arrays of cells with periodic boundary conditions, and if so, for which lengths.
For a block cellular automaton, testing reversibility is also easy: the automaton is reversible if and only if the transition function on the blocks of the automaton is invertible, and in this case the reverse automaton has the same block structure with the inverse transition function.[10]
However, for cellular automata with other neighborhoods in two or more dimensions, the problem of testing reversibility is undecidable, meaning that there cannot exist an algorithm that always halts and always correctly answers the problem. The proof of this fact by (Kari 1990) is based on the previously known undecidability of tiling the plane by Wang tiles, sets of square tiles with markings on their edges that constrain which pairs of tiles can fit edge-to-edge. Kari defines a cellular automaton from a set of Wang tiles, such that the automaton fails to be injective if and only if the given tile set can tile the entire plane. His construction uses the von Neumann neighborhood, and cells with large numbers of states. In the same paper, Kari also showed that it is undecidable to test whether a given cellular automaton rule of two or more dimensions is surjective (that is, whether it has a Garden of Eden).
Reverse neighborhood size
In a one-dimensional reversible cellular automaton with n states per cell, in which the neighborhood of a cell is an interval of m cells, the automaton representing the reverse dynamics has neighborhoods that consist of at most nm − 1 − m + 1 cells. This bound is known to be tight for m = 2: there exist n-state reversible cellular automata with two-cell neighborhoods whose time-reversed dynamics forms a cellular automaton with neighborhood size exactly n − 1.[25]
For any integer m there are only finitely many two-dimensional reversible m-state cellular automata with the von Neumann neighborhood. Therefore, there is a well-defined function f(m) such that all reverses of m-state cellular automata with the von Neumann neighborhood use a neighborhood with radius at most f(m): simply let f(m) be the maximum, among all of the finitely many reversible m-state cellular automata, of the neighborhood size needed to represent the time-reversed dynamics of the automaton. However, because of Kari's undecidability result, there is no algorithm for computing f(m) and the values of this function must grow very quickly, more quickly than any computable function.[12]
Wolfram's classification
A well-known classification of cellular automata by Stephen Wolfram studies their behavior on random initial conditions. For a reversible cellular automaton, if the initial configuration is chosen uniformly at random among all possible configurations, then that same uniform randomness continues to hold for all subsequent states. Thus it would appear that most reversible cellular automata are of Wolfram's Class 3: automata in which almost all initial configurations evolve pseudo-randomly or chaotically. However, it is still possible to distinguish among different reversible cellular automata by analyzing the effect of local perturbations on the behavior of the automaton. Making a change to the initial state of a reversible cellular automaton may cause changes to later states to remain only within a bounded region, to propagate irregularly but unboundedly, or to spread quickly, and (Wolfram 1984) lists one-dimensional reversible cellular automaton rules exhibiting all three of these types of behavior.
Later work by Wolfram identifies the one-dimensional Rule 37R automaton as being particularly interesting in this respect. When run on a finite array of cells with periodic boundary conditions, starting from a small seed of random cells centered within a larger empty neighborhood, it tends to fluctuate between ordered and chaotic states. However, with the same initial conditions on an unbounded set of cells its configurations tend to organize themselves into several types of simple moving particles.[26]
Abstract algebra
Another way to formalize reversible cellular automata involves abstract algebra, and this formalization has been useful in developing computerized searches for reversible cellular automaton rules. (Boykett 2004) defines a semicentral bigroupoid to be an algebraic structure consisting of a set S of elements and two operations → and ← on pairs of elements, satisfying the two equational axioms:
- for all elements a, b, and c in S, (a → b) ← (b → c) = b, and
- for all elements a, b, and c in S, (a ← b) → (b ← c) = b.
For instance, this is true for the two operations in which operation → returns its right argument and operation ← returns its left argument.
As Boykett argues, any one-dimensional reversible cellular automaton is equivalent to an automaton in rectangular form, in which the cells are offset a half unit at each time step, and in which both the forward and reverse evolution of the automaton have neighborhoods with just two cells, the cells a half unit away in each direction. If a reversible automaton has neighborhoods larger than two cells, it can be simulated by a reversible automaton with smaller neighborhoods and more states per cell, in which each cell of the simulating automaton simulates a contiguous block of cells in the simulated automaton. The two axioms of a semicentral bigroupoid are exactly the conditions required on the forward and reverse transition functions of these two-cell neighborhoods to be the reverses of each other. That is, every semicentral bigroupoid defines a reversible cellular automaton in rectangular form, in which the transition function of the automaton uses the → operation to combine the two cells of its neighborhood, and in which the ← operation similarly defines the reverse dynamics of the automaton. Every one-dimensional reversible cellular automaton is equivalent to one in this form.[5]
Boykett used this algebraic formulation as the basis for algorithms that exhaustively list all possible inequivalent reversible cellular automata.[27]
Conservation laws
When researchers design reversible cellular automata to simulate physical systems, they typically incorporate into the design the conservation laws of the system; for instance, a cellular automaton that simulates an ideal gas should conserve the number of gas particles and their total momentum, for otherwise it would not provide an accurate simulation. However, there has also been some research on the conservation laws that reversible cellular automata can have, independent of any intentional design. The typical type of conserved quantity measured in these studies takes the form of a sum, over all contiguous subsets of k cells of the automaton, of some numerical function of the states of the cells in each subset. Such a quantity is conserved if, whenever it takes a finite value, that value automatically remains constant through each time step of the automaton, and in this case it is called a kth-order invariant of the automaton.[28]
For instance, recall the one-dimensional cellular automaton defined as an example from a rectangular band, in which the cell states are pairs of values (l,r) drawn from sets L and R of left values and right values, the left value of each cell moves rightwards at each time step, and the right value of each cell moves leftwards. In this case, for each left or right value x of the band, one can define a conserved quantity, the total number of cells that have that value. If there are λ left values and ρ right values, then there are λ + ρ − 2 independent first-order-invariants, and any first-order invariant can be represented as a linear combination of these fundamental ones. The conserved quantities associated with left values flow uniformly to the right at a constant rate: that is, if the number of left values equal to x within some region C of the line takes a certain value at time 0, then it will take the same value for the shifted region C + t/2 at time t. Similarly, the conserved quantities associated with right values flow uniformly to the left.[29]
Any one-dimensional reversible cellular automaton may be placed into rectangular form, after which its transition rule may be factored into the action of an idempotent semicentral bigroupoid (a reversible rule for which regions of cells with a single state value change only at their boundaries) together with a permutation on the set of states. The first-order invariants for the idempotent lifting of the automaton rule (the modified rule formed by omitting the permutation) necessarily behave like the ones for a rectangular band: they have a basis of invariants that flow either leftwards or rightwards at a constant rate without interaction. The first-order invariants for the overall automaton are then exactly the invariants for the idempotent lifting that give equal weight to every pair of states that belong to the same orbit of the permutation. However, the permutation of states in the rule may cause these invariants to behave differently from in the idempotent lifting, flowing non-uniformly and with interactions.[29]
In physical systems, Noether's theorem provides an equivalence between conservation laws and symmetries of the system. However, for cellular automata this theorem does not directly apply, because instead of being governed by the energy of the system the behavior of the automaton is encoded into its rules, and the automaton is guaranteed to obey certain symmetries (translation invariance in both space and time) regardless of any conservation laws it might obey. Nevertheless, the conserved quantities of certain reversible systems behave similarly to energy in some respects. For instance, if different regions of the automaton have different average values of some conserved quantity, the automaton's rules may cause this quantity to dissipate, so that the distribution of the quantity is more uniform in later states. Using these conserved quantities as a stand-in for the energy of the system can allow it to be analyzed using methods from classical physics.[30]
Applications
Lattice gas automata
A lattice gas automaton is a cellular automaton designed to simulate the motion of particles in a fluid or an ideal gas. In such a system, gas particles move on straight lines with constant velocity, until undergoing elastic collision with other particles. Lattice gas automata simplify these models by only allowing a constant number of velocities (typically, only one speed and either four or six directions of motion) and by simplifying the types of collision that are possible.[31]
Specifically, the HPP lattice gas model consists of particles moving at unit velocity in the four axis-parallel directions. When two particles meet on the same line in opposite directions, they collide and are sent outwards from the collision point on the perpendicular line. This system obeys the conservation laws of physical gases, and produces simulations whose appearance resembles the behavior of physical gases. However, it was found to obey unrealistic additional conservation laws. For instance, the total momentum within any single line is conserved. As well, the differences between axis-parallel and non-axis-parallel directions in this model (its anisotropy) is undesirably high. The FHP lattice gas model improves the HPP model by having particles moving in six different directions, at 60 degree angles to each other, instead of only four directions. In any head-on collision, the two outgoing particles are deflected at 60 degree angles from the two incoming particles. Three-way collisions are also possible in the FHP model and are handled in a way that both preserves total momentum and avoids the unphysical added conservation laws of the HPP model.[31]
Because the motion of the particles in these systems is reversible, they are typically implemented with reversible cellular automata. In particular, both the HPP and FHP lattice gas automata can be implemented with a two-state block cellular automaton using the Margolus neighborhood.[31]
Ising model
The Ising model is used to model the behavior of magnetic systems. It consists of an array of cells, the state of each of which represents a spin, either up or down. The energy of the system is measured by a function that depends on the number of neighboring pairs of cells that have the same spin as each other. Therefore, if a cell has equal numbers of neighbors in the two states, it may flip its own state without changing the total energy. However, such a flip is energy-conserving only if no two adjacent cells flip at the same time.[32]
Cellular automaton models of this system divide the square lattice into two alternating subsets, and perform updates on one of the two subsets at a time. In each update, every cell that can flip does so. This defines a reversible cellular automaton which can be used to investigate the Ising model.[32]
Billiard-ball computation and low-power computing
(Fredkin Toffoli) proposed the billiard-ball computer as part of their investigations into reversible computing. A billiard-ball computer consists of a system of synchronized particles (the billiard balls) moving in tracks and guided by a fixed set of obstacles. When the particles collide with each other or with the obstacles, they undergo an elastic collision much as real billiard balls would do. The input to the computer is encoded using the presence or absence of particles on certain input tracks, and its output is similarly encoded using the presence or absence of particles on output tracks. The tracks themselves may be envisioned as wires, and the particles as being Boolean signals transported on those wires. When a particle hits an obstacle, it reflects from it. This reflection may be interpreted as a change in direction of the wire the particle is following. Two particles on different tracks may collide, forming a logic gate at their collision point.[33]
As (Margolus 1984) showed, billiard-ball computers may be simulated using a two-state reversible block cellular automaton with the Margolus neighborhood. In this automaton's update rule, blocks with exactly one live cell rotate by 180°, blocks with two diagonally opposite live cells rotate by 90°, and all other blocks remain unchanged. These rules cause isolated live cells to behave like billiard balls, moving on diagonal trajectories. Connected groups of more than one live cell behave instead like the fixed obstacles of the billiard-ball computer. In an appendix, Margolus also showed that a three-state second-order cellular automaton using the two-dimensional Moore neighborhood could simulate billiard-ball computers.
| Unsolved problem in mathematics: Is every three-dimensional reversible cellular automaton locally reversible? (more unsolved problems in mathematics)
|
One reason to study reversible universal models of computation such as the billiard-ball model is that they could theoretically lead to actual computer systems that consume very low quantities of energy. According to Landauer's principle, irreversible computational steps require a certain minimal amount of energy per step, but reversible steps can be performed with an amount of energy per step that is arbitrarily close to zero.[34] However, in order to perform computation using less energy than Landauer's bound, it is not good enough for a cellular automaton to have a transition function that is globally reversible: what is required is that the local computation of the transition function also be done in a reversible way. For instance, reversible block cellular automata are always locally reversible: the behavior of each individual block involves the application of an invertible function with finitely many inputs and outputs. (Toffoli Margolus) were the first to ask whether every reversible cellular automaton has a locally reversible update rule. (Kari 1996) showed that for one- and two-dimensional automata the answer is positive, and (Durand-Lose 2001) showed that any reversible cellular automaton could be simulated by a (possibly different) locally reversible cellular automaton. However, the question of whether every reversible transition function is locally reversible remains open for dimensions higher than two.[35]
Synchronization
The "Tron" rule of Toffoli and Margolus is a reversible block cellular rule with the Margolus neighborhood. When a 2 × 2 block of cells all have the same state, all cells of the block change state; in all other cases, the cells of the block remain unchanged. As Toffoli and Margolus argue, the evolution of patterns generated by this rule can be used as a clock to synchronize any other rule on the Margolus neighborhood. A cellular automaton synchronized in this way obeys the same dynamics as the standard Margolus-neighborhood rule while running on an asynchronous cellular automaton.[36]
Encryption
(Kari 1990) proposed using multidimensional reversible cellular automata as an encryption system. In Kari's proposal, the cellular automaton rule would be the encryption key. Encryption would be performed by running the rule forward one step, and decryption would be performed by running it backward one step. Kari suggests that a system such as this may be used as a public-key cryptosystem. In principle, an attacker could not algorithmically determine the decryption key (the reverse rule) from a given encryption key (forward rule) because of the undecidability of testing reversibility, so the forward rule could be made public without compromising the security of the system. However, Kari did not specify which types of reversible cellular automaton should be used for such a system, or show how a cryptosystem using this approach would be able to generate encryption/decryption key pairs.
(Chai Cao) have proposed an alternative encryption system. In their system, the encryption key determines the local rule for each cell of a one-dimensional cellular automaton. A second-order automaton based on that rule is run for several rounds on an input to transform it into an encrypted output. The reversibility property of the automaton ensures that any encrypted message can be decrypted by running the same system in reverse. In this system, keys must be kept secret, because the same key is used both for encryption and decryption.
Quantum computing
Quantum cellular automata are arrays of automata whose states and state transitions obey the laws of quantum dynamics. Quantum cellular automata were suggested as a model of computation by (Feynman 1982) and first formalized by (Watrous 1995). Several competing notions of these automata remain under research, many of which require that the automata constructed in this way be reversible.[37]
Physical universality
(Janzing 2010) asked whether it was possible for a cellular automaton to be physically universal, meaning that, for any bounded region of the automaton's cells, it should be possible to surround that region with cells whose states form an appropriate support scaffolding that causes the automaton to implement any arbitrary transformation on sets of states within the region. Such an automaton must be reversible, or at least locally injective, because automata without this property have Garden of Eden patterns, and it is not possible to implement a transformation that creates a Garden of Eden.
(Schaeffer 2015) constructed a reversible cellular automaton that is physically universal in this sense. Schaeffer's automaton is a block cellular automaton with two states and the Margolis neighborhood, closely related to the automata for the billiard ball model and for the HPP lattice gas. However, the billiard ball model is not physically universal, as it can be used to construct impenetrable walls preventing the state within some region from being read and transformed. In Schaeffer's model, every pattern eventually decomposes into particles moving diagonally in four directions. Thus, his automaton is not Turing complete. However, Schaeffer showed that it is possible to surround any finite configuration by scaffolding that decays more slowly than it. After the configuration decomposes into particles, the scaffolding intercepts those particles, and uses them as the input to a system of Boolean circuits constructed within the scaffolding. These circuits can be used to compute arbitrary functions of the initial configuration. The scaffolding then translates the output of the circuits back into a system of moving particles, which converge on the initial region and collide with each other to build a copy of the transformed state. In this way, Schaeffer's system can be used to apply any function to any bounded region of the state space, showing that this automaton rule is physically universal.[38]
Notes
- ↑ (Wolfram 2002), p. 1018.
- ↑ (Schiff 2008), p. 44.
- ↑ Toffoli & Margolus (1990).
- ↑ (Blanchard Devaney), p. 38: "The shift map is without doubt the fundamental object in symbolic dynamics."
- ↑ 5.0 5.1 Boykett (2004).
- ↑ (Wolfram 2002), p. 1093.
- ↑ Patt (1971).
- ↑ 8.0 8.1 (Sutner 1991).
- ↑ 9.0 9.1 9.2 (Toffoli Margolus), section 12.8.2, "Critters", pp. 132–134; (Margolus 1999); (Marotta 2005).
- ↑ 10.0 10.1 10.2 (Toffoli Margolus), Section 14.5, "Partitioning technique", pp. 150–153; (Schiff 2008), Section 4.2.1, "Partitioning Cellular Automata", pp. 115–116.
- ↑ (Toffoli Margolus), Chapter 12, "The Margolus Neighborhood", pp. 119–138.
- ↑ 12.0 12.1 (Kari 2005).
- ↑ (Margolus 1984); (Vichniac 1984); (Wolfram 1984).
- ↑ 14.0 14.1 14.2 (Toffoli Margolus), Section 14.2, "Second-order technique", pp. 147–149. (Wolfram 2002), pp. 437ff. (McIntosh 2009).
- ↑ 15.0 15.1 (Toffoli Margolus), section 5.3, "Conserved-landscape permutations", pp. 237–238.
- ↑ Miller & Fredkin (2005).
- ↑ Miller & Fredkin (2012).
- ↑ In the one-dimensional case, several of these equivalences were already presented, in the language of dynamical systems rather than cellular automata, by (Hedlund 1969), Theorem 4.1. For higher dimensions, see (Richardson 1972) and (Di Gregorio Trautteur).
- ↑ Myhill (1963).
- ↑ Richardson (1972).
- ↑ Hedlund (1969).
- ↑ Moraal (2000).
- ↑ Culik cites a 1979 automata theory textbook for this result, but see (Béal Carton) for more recent developments on efficiently testing whether a transducer defines a function.
- ↑ Neither (Amoroso Patt) nor (Culik 1987) state their algorithms' time complexities explicitly, but (Sutner 1991) does, and this bound can also be found e.g. in (Czeizler Kari).
- ↑ (Kari 1992); (Czeizler 2004); (Czeizler Kari).
- ↑ (Wolfram 2002), pp. 454–457.
- ↑ (Boykett 2004). See (Hillman 1991) and (Seck Tuoh Mora Chapa Vergara) for closely related work on the enumeration of width-2 reversible cellular automata.
- ↑ (Hattori Takesue); (Fukś 2007).
- ↑ 29.0 29.1 Boykett, Kari & Taati (2008).
- ↑ (Pomeau 1984); (Takesue 1990); (Capobianco Toffoli).
- ↑ 31.0 31.1 31.2 (Toffoli Margolus), Chapter 16, "Fluid dynamics", pp. 172–184.
- ↑ 32.0 32.1 (Toffoli Margolus), Chapter 17.2, "Ising systems", pp. 186–190.
- ↑ (Durand-Lose 2002).
- ↑ Fredkin & Toffoli (1982).
- ↑ Kari (2005, 2009)
- ↑ (Toffoli Margolus), Section 12.8.3, "Asynchronous computation", pp. 134–136.
- ↑ (Meyer 1996); (Schumacher Werner); (Shepherd Franz); (Nagaj Wocjan).
- ↑ See also "A Physically Universal Cellular Automaton", Shtetl-Optimized, Scott Aaronson, June 26, 2014.
References
- Amoroso, S. (1972), "Decision procedures for surjectivity and injectivity of parallel maps for tessellation structures", Journal of Computer and System Sciences 6 (5): 448–464, doi:10.1016/S0022-0000(72)80013-8.
- Béal, Marie-Pierre; Carton, Olivier; Prieur, Christophe; Sakarovitch, Jacques (2003), "Squaring transducers: an efficient procedure for deciding functionality and sequentiality", Theoretical Computer Science 292 (1): 45–63, doi:10.1016/S0304-3975(01)00214-6.
- Blanchard, Paul (2004), "Complex dynamics and symbolic dynamics", in Williams, Susan G., Symbolic Dynamics and its Applications, Proceedings of Symposia in Applied Mathematics, 60, Providence, RI: American Mathematical Society, pp. 37–60, doi:10.1090/psapm/060/2078845.
- Boykett, Tim (2004), "Efficient exhaustive listings of reversible one dimensional cellular automata", Theoretical Computer Science 325 (2): 215–247, doi:10.1016/j.tcs.2004.06.007.
- Boykett, Tim; Kari, Jarkko; Taati, Siamak (2008), "Conservation laws in rectangular CA", Journal of Cellular Automata 3 (2): 115–122, http://pub.math.leidenuniv.nl/~taatis/articles/conslaws06.pdf.
- Capobianco, Silvio (2011), "Can anything from Noether's theorem be salvaged for discrete dynamical systems?", Proceedings of the 10th International Conference on Unconventional Computation (UC 2011), Lecture Notes in Computer Science, 6714, Springer-Verlag, pp. 77–88, doi:10.1007/978-3-642-21341-0_13.
- Chai, Zhenchuan; Cao, Zhenfu; Zhou, Yuan (2005), "Encryption based on reversible second-order cellular automata", Parallel and Distributed Processing and Applications (ISPA 2005 Workshops), Lecture Notes in Computer Science, 3759, Springer-Verlag, pp. 350–358, doi:10.1007/11576259_39.
- Culik, Karel II (1987), "On invertible cellular automata", Complex Systems 1 (6): 1035–1044, http://www.complex-systems.com/pdf/01-6-1.pdf.
- Czeizler, Eugen (2004), "On the size of the inverse neighborhoods for one-dimensional reversible cellular automata", Theoretical Computer Science 325 (2): 273–284, doi:10.1016/j.tcs.2004.06.009.
- Czeizler, Eugen (2007), "A tight linear bound on the synchronization delay of bijective automata", Theoretical Computer Science 380 (1–2): 23–36, doi:10.1016/j.tcs.2007.02.052.
- Di Gregorio, S.; Trautteur, G. (1975), "On reversibility in cellular automata", Journal of Computer and System Sciences 11 (3): 382–391, doi:10.1016/S0022-0000(75)80059-6.
- Durand-Lose, Jérôme (2001), "Representing reversible cellular automata with reversible block cellular automata", Discrete models: combinatorics, computation, and geometry (Paris, 2001), Discrete Math. Theor. Comput. Sci. Proc., AA, Maison Inform. Math. Discrèt. (MIMD), Paris, pp. 145–154.
- Durand-Lose, Jérôme (2002), "Computing inside the billiard ball model", Collision-Based Computing, Springer-Verlag, pp. 135–160.
- "Simulating physics with computers", International Journal of Theoretical Physics 21 (6–7): 467–488, 1982, doi:10.1007/BF02650179, Bibcode: 1982IJTP...21..467F.
- "Conservative logic", International Journal of Theoretical Physics 21 (3–4): 219–253, 1982, doi:10.1007/BF01857727, Bibcode: 1982IJTP...21..219F. Reprinted in Collision-Based Computing, Springer-Verlag, 2002, pp. 47–82.
- Fukś, Henryk (2007), "Remarks on the critical behavior of second order additive invariants in elementary cellular automata", Fundamenta Informaticae 78 (3): 329–341, Bibcode: 2005nlin......2037F.
- Hattori, Tetsuya; Takesue, Shinji (1991), "Additive conserved quantities in discrete-time lattice dynamical systems", Physica D: Nonlinear Phenomena 49 (3): 295–322, doi:10.1016/0167-2789(91)90150-8, Bibcode: 1991PhyD...49..295H.
- "Endomorphisms and automorphisms of the shift dynamical systems", Mathematical Systems Theory 3 (4): 320–375, 1969, doi:10.1007/BF01691062.
- Hertling, Peter (1998), "Embedding cellular automata into reversible ones", Unconventional models of computation (Auckland, 1998), Springer Series in Discrete Mathematics and Theoretical Computer Science, Springer-Verlag, pp. 243–256.
- Hillman, David (1991), "The structure of reversible one-dimensional cellular automata", Physica D: Nonlinear Phenomena 52 (2–3): 277–292, doi:10.1016/0167-2789(91)90128-V, Bibcode: 1991PhyD...52..277H.
- Janzing, Dominik (2010), Is there a physically universal cellular automaton or Hamiltonian?, Bibcode: 2010arXiv1009.1720J.
- "Reversibility of 2D cellular automata is undecidable", Physica D: Nonlinear Phenomena 45 (1–3): 379–385, 1990, doi:10.1016/0167-2789(90)90195-U, Bibcode: 1990PhyD...45..379K.
- "On the inverse neighborhoods of reversible cellular automata", Lindenmayer Systems: Impacts on Theoretical Computer Science, Computer Graphics, and Developmental Biology, Springer-Verlag, 1992, pp. 477–495, doi:10.1007/978-3-642-58117-5_29.
- "Representation of reversible cellular automata with block permutations", Mathematical Systems Theory 29 (1): 47–61, 1996, doi:10.1007/BF01201813.
- "Reversible cellular automata", Developments in Language Theory: 9th International Conference, DLT 2005, Palermo, Italy, July 4–8, 2005, Proceedings, Lecture Notes in Computer Science, 3572, Springer-Verlag, 2005, pp. 2–23, doi:10.1007/11505877_5, http://copper.math.buffalo.edu/urgewiki/uploads/Literature2010Carbonara/Kari2005.pdf.
- "Structure of reversible cellular automata", Unconventional Computation: 8th International Conference, UC 2009, Ponta Delgada, Portugal, September 7–11, 2009, Proceedings, Lecture Notes in Computer Science, 5715, Springer-Verlag, 2009, p. 6, doi:10.1007/978-3-642-03745-0_5, Bibcode: 2009LNCS.5715....6K.
- "Physics-like models of computation", Physica D: Nonlinear Phenomena 10 (1–2): 81–95, 1984, doi:10.1016/0167-2789(84)90252-5, Bibcode: 1984PhyD...10...81M. Reprinted in Theory and Applications of Cellular Automata, Advanced series on complex systems, 1, World Scientific, 1986, pp. 232–246, Bibcode: 1986taca.book.....W, and in Collision-Based Computing, Springer-Verlag, 2002, pp. 83–104.
- Hey, Anthony J. G., ed. (1999), "Crystalline computation", Feynman and Computation, Perseus Books, pp. 267–305, Bibcode: 1998comp.gas.11002M.
- Marotta, Sebastian M. (2005), "Living in Critters' world", Revista Ciências Exatas e Naturais 7 (1), http://web01.unicentro.br/revistas/index.php/RECEN/article/viewFile/385/537.
- "12. Reversible cellular automata", One Dimensional Cellular Automata, Luniver Press, 2009, pp. 205–246.
- Meyer, David A. (1996), "From quantum cellular automata to quantum lattice gases", Journal of Statistical Physics 85 (5–6): 551–574, doi:10.1007/BF02199356, Bibcode: 1996JSP....85..551M.
- Miller, Daniel B. (2005), "Two-state, reversible, universal cellular automata in three dimensions", Proceedings of the 2nd Conference on Computing Frontiers (CF '05), New York, NY, USA: ACM, pp. 45–51, doi:10.1145/1062261.1062271, ISBN 1-59593-019-1.
- Miller, Daniel B. (2012), Circular motion of strings in cellular automata, and other surprises, Bibcode: 2012arXiv1206.2060M.
- Moraal, Hendrik (2000), "Graph-theoretical characterization of invertible cellular automata", Physica D: Nonlinear Phenomena 141 (1–2): 1–18, doi:10.1016/S0167-2789(00)00020-8, Bibcode: 2000PhyD..141....1M.
- Morita, Kenichi (1995), "Reversible simulation of one-dimensional irreversible cellular automata", Theoretical Computer Science 148 (1): 157–163, doi:10.1016/0304-3975(95)00038-X.
- Myhill, John (1963), "The converse of Moore's Garden-of-Eden theorem", Proceedings of the American Mathematical Society 14 (4): 685–686, doi:10.2307/2034301. Reprinted in Essays on Cellular Automata, University of Illinois Press, 1970, pp. 204–205.
- Nagaj, Daniel; Wocjan, Pawel (2008), "Hamiltonian quantum cellular automata in one dimension", Physical Review A 78 (3): 032311, doi:10.1103/PhysRevA.78.032311, Bibcode: 2008PhRvA..78c2311N.
- Injections of neighborhood size three and four on the set of configurations from the infinite one-dimensional tessellation automata of two-state cells, Technical Report ECON-N1-P-1, Ft. Monmouth, NJ 07703, 1971. As cited by (Amoroso Patt) and (Toffoli Margolus).
- "Invariants in cellular automata", Journal of Physics A: Mathematical and General 17 (8): L415–L418, 1984, doi:10.1088/0305-4470/17/8/004, Bibcode: 1984JPhA...17L.415P.
- Richardson, D. (1972), "Tessellations with local transformations", Journal of Computer and System Sciences 6 (5): 373–388, doi:10.1016/S0022-0000(72)80009-6.
- Schaeffer, Luke (2015), "A physically universal cellular automaton", Proceedings of the 6th Innovations in Theoretical Computer Science Conference (ITCS 2015), Association for Computing Machinery, pp. 237–246, doi:10.1145/2688073.2688107, ECCC TR14-084.
- Schiff, Joel L. (2008), Cellular Automata: A Discrete View of the World, Wiley, ISBN 978-0-470-16879-0.
- Reversible quantum cellular automata, 2004, Bibcode: 2004quant.ph..5174S.
- Seck Tuoh Mora, Juan Carlos; Chapa Vergara, Sergio V.; Juárez Martínez, Genaro (2005), "Procedures for calculating reversible one-dimensional cellular automata", Physica D: Nonlinear Phenomena 202 (1–2): 134–141, doi:10.1016/j.physd.2005.01.018, Bibcode: 2005PhyD..202..134S, http://eprints.uwe.ac.uk/7891/1/procedureRCA.pdf.
- Shepherd, D. J.; Franz, T.; Werner, R. F. (2006), "A universally programmable quantum cellular automaton", Physical Review Letters 97 (2): 020502, doi:10.1103/PhysRevLett.97.020502, PMID 16907423, Bibcode: 2006PhRvL..97b0502S.
- "De Bruijn graphs and linear cellular automata", Complex Systems 5: 19–30, 1991, http://www.complex-systems.com/pdf/05-1-3.pdf.
- Takesue, Shinji (1990), "Relaxation properties of elementary reversible cellular automata", Physica D: Nonlinear Phenomena 45 (1–3): 278–284, doi:10.1016/0167-2789(90)90195-U, Bibcode: 1990PhyD...45..379K.
- "Computation and construction universality of reversible cellular automata", Journal of Computer and System Sciences 15 (2): 213–231, 1977, doi:10.1016/S0022-0000(77)80007-X.
- Toffoli, Tommaso; Margolus, Norman (1987), Cellular Automata Machines: A New Environment for Modeling, MIT Press, ISBN 978-0-262-20060-8, https://archive.org/details/cellularautomata00toff.
- "Invertible cellular automata: a review", Physica D: Nonlinear Phenomena 45 (1–3): 229–253, 1990, doi:10.1016/0167-2789(90)90185-R, Bibcode: 1990PhyD...45..229T.
- Vichniac, Gérard Y. (1984), "Simulating physics with cellular automata", Physica D: Nonlinear Phenomena 10 (1–2): 96–115, doi:10.1016/0167-2789(84)90253-7, Bibcode: 1984PhyD...10...96V.
- "On one-dimensional quantum cellular automata", Proceedings of the 36th Annual Symposium on Foundations of Computer Science (Milwaukee, WI, 1995), Los Alamitos, CA: IEEE Computer Society Press, 1995, pp. 528–537, doi:10.1109/SFCS.1995.492583.
- "Cellular automata as models of complexity", Nature 311 (5985): 419–424, 1984, doi:10.1038/311419a0, Bibcode: 1984Natur.311..419W, http://www.stephenwolfram.com/publications/academic/cellular-automata-models-complexity.pdf.
- A New Kind of Science, Wolfram Media, 2002, ISBN 1-57955-008-8
 |