Schur–Horn theorem
In mathematics, particularly linear algebra, the Schur–Horn theorem, named after Issai Schur and Alfred Horn, characterizes the diagonal of a Hermitian matrix with given eigenvalues. It has inspired investigations and substantial generalizations in the setting of symplectic geometry. A few important generalizations are Kostant's convexity theorem, Atiyah–Guillemin–Sternberg convexity theorem, Kirwan convexity theorem.
Statement
Schur–Horn theorem — Theorem. Let [math]\displaystyle{ d_1, \dots, d_N }[/math] and [math]\displaystyle{ \lambda_1, \dots, \lambda_N }[/math] be two sequences of real numbers arranged in a non-increasing order. There is a Hermitian matrix with diagonal values [math]\displaystyle{ d_1, \dots, d_N }[/math] (in this order, starting with [math]\displaystyle{ d_1 }[/math] at the top-left) and eigenvalues [math]\displaystyle{ \lambda_1, \dots, \lambda_N }[/math] if and only if [math]\displaystyle{ \sum_{i=1}^n d_i \leq \sum_{i=1}^n \lambda_i \qquad n = 1, \dots, N-1 }[/math] and [math]\displaystyle{ \sum_{i=1}^N d_i = \sum_{i=1}^N \lambda_i. }[/math]
The inequalities above may alternatively be written: [math]\displaystyle{ \begin{alignat}{7} d_1 &\;\leq\;&& \lambda_1 \\[0.3ex] d_2 + d_1 &\;\leq&& \lambda_1 + \lambda_2 \\[0.3ex] \vdots &\;\leq&& \vdots \\[0.3ex] d_{N-1} + \cdots + d_2 + d_1 &\;\leq&& \lambda_1 + \lambda_2 + \cdots + \lambda_{N-1} \\[0.3ex] d_N + d_{N-1} + \cdots + d_2 + d_1 &\;=&& \lambda_1 + \lambda_2 + \cdots + \lambda_{N-1} + \lambda_N. \\[0.3ex] \end{alignat} }[/math]
The Schur–Horn theorem may thus be restated more succinctly and in plain English:
- Schur–Horn theorem: Given any non-increasing real sequences of desired diagonal elements [math]\displaystyle{ d_1 \geq \cdots \geq d_N }[/math] and desired eigenvalues [math]\displaystyle{ \lambda_1 \geq \cdots \geq \lambda_N, }[/math] there exists a Hermitian matrix with these eigenvalues and diagonal elements if and only if these two sequences have the same sum and for every possible integer [math]\displaystyle{ n, }[/math] the sum of the first [math]\displaystyle{ n }[/math] desired diagonal elements never exceeds the sum of the first [math]\displaystyle{ n }[/math] desired eigenvalues.
Reformation allowing unordered diagonals and eigenvalues
Although this theorem requires that [math]\displaystyle{ d_1 \geq \cdots \geq d_N }[/math] and [math]\displaystyle{ \lambda_1 \geq \cdots \geq \lambda_N }[/math] be non-increasing, it is possible to reformulate this theorem without these assumptions.
We start with the assumption [math]\displaystyle{ \lambda_1 \geq \cdots \geq \lambda_N. }[/math] The left hand side of the theorem's characterization (that is, "there exists a Hermitian matrix with these eigenvalues and diagonal elements") depends on the order of the desired diagonal elements [math]\displaystyle{ d_1, \dots, d_N }[/math] (because changing their order would change the Hermitian matrix whose existence is in question) but it does not depend on the order of the desired eigenvalues [math]\displaystyle{ \lambda_1, \dots, \lambda_N. }[/math]
On the right hand right hand side of the characterization, only the values of [math]\displaystyle{ \lambda_1 + \cdots + \lambda_n }[/math] depend on the assumption [math]\displaystyle{ \lambda_1 \geq \cdots \geq \lambda_N. }[/math] Notice that this assumption means that the expression [math]\displaystyle{ \lambda_1 + \cdots + \lambda_n }[/math] is just notation for the sum of the [math]\displaystyle{ n }[/math] largest desired eigenvalues. Replacing the expression [math]\displaystyle{ \lambda_1 + \cdots + \lambda_n }[/math] with this written equivalent makes the assumption [math]\displaystyle{ \lambda_1 \geq \cdots \geq \lambda_N }[/math] completely unnecessary:
- Schur–Horn theorem: Given any [math]\displaystyle{ N }[/math] desired real eigenvalues and a non-increasing real sequence of desired diagonal elements [math]\displaystyle{ d_1 \geq \cdots \geq d_N, }[/math] there exists a Hermitian matrix with these eigenvalues and diagonal elements if and only if these two sequences have the same sum and for every possible integer [math]\displaystyle{ n, }[/math] the sum of the first [math]\displaystyle{ n }[/math] desired diagonal elements never exceeds the sum of the [math]\displaystyle{ n }[/math] largest desired eigenvalues.
Permutation polytope generated by a vector
The permutation polytope generated by [math]\displaystyle{ \tilde{x} = (x_1, x_2,\ldots, x_n) \in \Reals^n }[/math] denoted by [math]\displaystyle{ \mathcal{K}_{\tilde{x}} }[/math] is defined as the convex hull of the set [math]\displaystyle{ \{(x_{\pi(1)},x_{\pi(2)},\ldots,x_{\pi(n)}) \in \Reals^n : \pi \in S_n\}. }[/math] Here [math]\displaystyle{ S_n }[/math] denotes the symmetric group on [math]\displaystyle{ \{1, 2, \ldots, n\}. }[/math] In other words, the permutation polytope generated by [math]\displaystyle{ (x_1, \dots, x_n) }[/math] is the convex hull of the set of all points in [math]\displaystyle{ \Reals^n }[/math] that can be obtained by rearranging the coordinates of [math]\displaystyle{ (x_1, \dots, x_n). }[/math] The permutation polytope of [math]\displaystyle{ (1, 1, 2), }[/math] for instance, is the convex hull of the set [math]\displaystyle{ \{(1, 1, 2), (1, 2, 1), (2, 1, 1)\}, }[/math] which in this case is the solid (filled) triangle whose vertices are the three points in this set. Notice, in particular, that rearranging the coordinates of [math]\displaystyle{ (x_1, \dots, x_n) }[/math] does not change the resulting permutation polytope; in other words, if a point [math]\displaystyle{ \tilde{y} }[/math] can be obtained from [math]\displaystyle{ \tilde{x} = (x_1, \dots, x_n) }[/math] by rearranging its coordinates, then [math]\displaystyle{ \mathcal{K}_{\tilde{y}} = \mathcal{K}_{\tilde{x}}. }[/math]
The following lemma characterizes the permutation polytope of a vector in [math]\displaystyle{ \Reals^n. }[/math]
Lemma[1][2] — If [math]\displaystyle{ x_1 \geq \cdots \geq x_n, }[/math] and [math]\displaystyle{ y_1 \geq \cdots \geq y_n, }[/math] have the same sum [math]\displaystyle{ x_1 + \cdots + x_n = y_1 + \cdots + y_n, }[/math] then the following statements are equivalent:
- [math]\displaystyle{ \tilde{y} := (y_1, \cdots, y_n) \in \mathcal{K}_{\tilde{x}}. }[/math]
- [math]\displaystyle{ y_1 \leq x_1, }[/math] and [math]\displaystyle{ y_1 + y_2 \leq x_1 + x_2, }[/math] and [math]\displaystyle{ \ldots, }[/math] and [math]\displaystyle{ y_1 + y_2 + \cdots + y_{n-1} \leq x_1 + x_2 + \cdots + x_{n-1} }[/math]
- There exist a sequence of points [math]\displaystyle{ \tilde{x}_1, \dots, \tilde{x}_n }[/math] in [math]\displaystyle{ \mathcal{K}_{\tilde{x}}, }[/math] starting with [math]\displaystyle{ \tilde{x}_1 = \tilde{x} }[/math] and ending with [math]\displaystyle{ \tilde{x}_n = \tilde{y} }[/math] such that [math]\displaystyle{ \tilde{x}_{k+1} = t \tilde{x}_k + (1-t) \tau(\tilde{x_k}) }[/math] for each [math]\displaystyle{ k }[/math] in [math]\displaystyle{ \{1, 2, \ldots, n-1\}, }[/math] some transposition [math]\displaystyle{ \tau }[/math] in [math]\displaystyle{ S_n, }[/math] and some [math]\displaystyle{ t }[/math] in [math]\displaystyle{ [0,1], }[/math] depending on [math]\displaystyle{ k. }[/math]
Reformulation of Schur–Horn theorem
In view of the equivalence of (i) and (ii) in the lemma mentioned above, one may reformulate the theorem in the following manner.
Theorem. Let [math]\displaystyle{ d_1, \dots, d_N }[/math] and [math]\displaystyle{ \lambda_1, \dots, \lambda_N }[/math] be real numbers. There is a Hermitian matrix with diagonal entries [math]\displaystyle{ d_1, \dots, d_N }[/math] and eigenvalues [math]\displaystyle{ \lambda_1, \dots, \lambda_N }[/math] if and only if the vector [math]\displaystyle{ (d_1, \ldots, d_n) }[/math] is in the permutation polytope generated by [math]\displaystyle{ (\lambda_1, \ldots, \lambda_n). }[/math]
Note that in this formulation, one does not need to impose any ordering on the entries of the vectors [math]\displaystyle{ d_1, \dots, d_N }[/math] and [math]\displaystyle{ \lambda_1, \dots, \lambda_N. }[/math]
Proof of the Schur–Horn theorem
Let [math]\displaystyle{ A = (a_{jk}) }[/math] be a [math]\displaystyle{ n \times n }[/math] Hermitian matrix with eigenvalues [math]\displaystyle{ \{\lambda_i\}_{i=1}^n, }[/math] counted with multiplicity. Denote the diagonal of [math]\displaystyle{ A }[/math] by [math]\displaystyle{ \tilde{a}, }[/math] thought of as a vector in [math]\displaystyle{ \Reals^n, }[/math] and the vector [math]\displaystyle{ (\lambda_1, \lambda_2, \ldots, \lambda_n) }[/math] by [math]\displaystyle{ \tilde{\lambda}. }[/math] Let [math]\displaystyle{ \Lambda }[/math] be the diagonal matrix having [math]\displaystyle{ \lambda_1, \lambda_2, \ldots, \lambda_n }[/math] on its diagonal.
([math]\displaystyle{ \Rightarrow }[/math]) [math]\displaystyle{ A }[/math] may be written in the form [math]\displaystyle{ U \Lambda U^{-1}, }[/math] where [math]\displaystyle{ U }[/math] is a unitary matrix. Then [math]\displaystyle{ a_{ii} = \sum_{j=1}^n \lambda_j |u_{ij}|^2, \; i = 1, 2, \ldots, n. }[/math]
Let [math]\displaystyle{ S = (s_{ij}) }[/math] be the matrix defined by [math]\displaystyle{ s_{ij} = |u_{ij}|^2. }[/math] Since [math]\displaystyle{ U }[/math] is a unitary matrix, [math]\displaystyle{ S }[/math] is a doubly stochastic matrix and we have [math]\displaystyle{ \tilde{a} = S\tilde{\lambda}. }[/math] By the Birkhoff–von Neumann theorem, [math]\displaystyle{ S }[/math] can be written as a convex combination of permutation matrices. Thus [math]\displaystyle{ \tilde{a} }[/math] is in the permutation polytope generated by [math]\displaystyle{ \tilde{\lambda}. }[/math] This proves Schur's theorem.
([math]\displaystyle{ \Leftarrow }[/math]) If [math]\displaystyle{ \tilde{a} }[/math] occurs as the diagonal of a Hermitian matrix with eigenvalues [math]\displaystyle{ \{\lambda_i\}_{i=1}^n, }[/math] then [math]\displaystyle{ t\tilde{a} + (1-t)\tau(\tilde{a}) }[/math] also occurs as the diagonal of some Hermitian matrix with the same set of eigenvalues, for any transposition [math]\displaystyle{ \tau }[/math] in [math]\displaystyle{ S_n. }[/math] One may prove that in the following manner.
Let [math]\displaystyle{ \xi }[/math] be a complex number of modulus [math]\displaystyle{ 1 }[/math] such that [math]\displaystyle{ \overline{\xi a_{jk}} = - \xi a_{jk} }[/math] and [math]\displaystyle{ U }[/math] be a unitary matrix with [math]\displaystyle{ \xi \sqrt{t}, \sqrt{t} }[/math] in the [math]\displaystyle{ j, j }[/math] and [math]\displaystyle{ k, k }[/math] entries, respectively, [math]\displaystyle{ -\sqrt{1-t}, \xi \sqrt{1-t} }[/math] at the [math]\displaystyle{ j, k }[/math] and [math]\displaystyle{ k, j }[/math] entries, respectively, [math]\displaystyle{ 1 }[/math] at all diagonal entries other than [math]\displaystyle{ j, j }[/math] and [math]\displaystyle{ k, k, }[/math] and [math]\displaystyle{ 0 }[/math] at all other entries. Then [math]\displaystyle{ UAU^{-1} }[/math] has [math]\displaystyle{ ta_{jj} + (1-t)a_{kk} }[/math] at the [math]\displaystyle{ j, j }[/math] entry, [math]\displaystyle{ (1-t)a_{jj} + ta_{kk} }[/math] at the [math]\displaystyle{ k,k }[/math] entry, and [math]\displaystyle{ a_{ll} }[/math] at the [math]\displaystyle{ l,l }[/math] entry where [math]\displaystyle{ l \neq j, k. }[/math] Let [math]\displaystyle{ \tau }[/math] be the transposition of [math]\displaystyle{ \{1, 2, \dots, n\} }[/math] that interchanges [math]\displaystyle{ j }[/math] and [math]\displaystyle{ k. }[/math]
Then the diagonal of [math]\displaystyle{ UAU^{-1} }[/math] is [math]\displaystyle{ t\tilde{a} + (1-t)\tau(\tilde{a}). }[/math]
[math]\displaystyle{ \Lambda }[/math] is a Hermitian matrix with eigenvalues [math]\displaystyle{ \{ \lambda_i \}_{i=1}^n. }[/math] Using the equivalence of (i) and (iii) in the lemma mentioned above, we see that any vector in the permutation polytope generated by [math]\displaystyle{ (\lambda_1, \lambda_2, \ldots, \lambda_n), }[/math] occurs as the diagonal of a Hermitian matrix with the prescribed eigenvalues. This proves Horn's theorem.
Symplectic geometry perspective
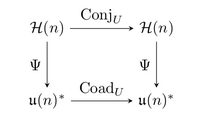
The Schur–Horn theorem may be viewed as a corollary of the Atiyah–Guillemin–Sternberg convexity theorem in the following manner. Let [math]\displaystyle{ \mathcal{U}(n) }[/math] denote the group of [math]\displaystyle{ n \times n }[/math] unitary matrices. Its Lie algebra, denoted by [math]\displaystyle{ \mathfrak{u}(n), }[/math] is the set of skew-Hermitian matrices. One may identify the dual space [math]\displaystyle{ \mathfrak{u}(n)^* }[/math] with the set of Hermitian matrices [math]\displaystyle{ \mathcal{H}(n) }[/math] via the linear isomorphism [math]\displaystyle{ \Psi : \mathcal{H}(n) \rightarrow \mathfrak{u}(n)^* }[/math] defined by [math]\displaystyle{ \Psi(A)(B) = \mathrm{tr}(iAB) }[/math] for [math]\displaystyle{ A \in \mathcal{H}(n), B \in \mathfrak{u}(n). }[/math] The unitary group [math]\displaystyle{ \mathcal{U}(n) }[/math] acts on [math]\displaystyle{ \mathcal{H}(n) }[/math] by conjugation and acts on [math]\displaystyle{ \mathfrak{u}(n)^* }[/math] by the coadjoint action. Under these actions, [math]\displaystyle{ \Psi }[/math] is an [math]\displaystyle{ \mathcal{U}(n) }[/math]-equivariant map i.e. for every [math]\displaystyle{ U \in \mathcal{U}(n) }[/math] the following diagram commutes,
Let [math]\displaystyle{ \tilde{\lambda} = (\lambda_1, \lambda_2, \ldots, \lambda_n) \in \Reals^n }[/math] and [math]\displaystyle{ \Lambda \in \mathcal{H}(n) }[/math] denote the diagonal matrix with entries given by [math]\displaystyle{ \tilde{\lambda}. }[/math] Let [math]\displaystyle{ \mathcal{O}_{\tilde{\lambda}} }[/math] denote the orbit of [math]\displaystyle{ \Lambda }[/math] under the [math]\displaystyle{ \mathcal{U}(n) }[/math]-action i.e. conjugation. Under the [math]\displaystyle{ \mathcal{U}(n) }[/math]-equivariant isomorphism [math]\displaystyle{ \Psi, }[/math] the symplectic structure on the corresponding coadjoint orbit may be brought onto [math]\displaystyle{ \mathcal{O}_{\tilde{\lambda}}. }[/math] Thus [math]\displaystyle{ \mathcal{O}_{\tilde{\lambda}} }[/math] is a Hamiltonian [math]\displaystyle{ \mathcal{U}(n) }[/math]-manifold.
Let [math]\displaystyle{ \mathbb{T} }[/math] denote the Cartan subgroup of [math]\displaystyle{ \mathcal{U}(n) }[/math] which consists of diagonal complex matrices with diagonal entries of modulus [math]\displaystyle{ 1. }[/math] The Lie algebra [math]\displaystyle{ \mathfrak{t} }[/math] of [math]\displaystyle{ \mathbb{T} }[/math] consists of diagonal skew-Hermitian matrices and the dual space [math]\displaystyle{ \mathfrak{t}^* }[/math] consists of diagonal Hermitian matrices, under the isomorphism [math]\displaystyle{ \Psi. }[/math] In other words, [math]\displaystyle{ \mathfrak{t} }[/math] consists of diagonal matrices with purely imaginary entries and [math]\displaystyle{ \mathfrak{t}^* }[/math] consists of diagonal matrices with real entries. The inclusion map [math]\displaystyle{ \mathfrak{t} \hookrightarrow \mathfrak{u}(n) }[/math] induces a map [math]\displaystyle{ \Phi : \mathcal{H}(n) \cong \mathfrak{u}(n)^* \rightarrow \mathfrak{t}^*, }[/math] which projects a matrix [math]\displaystyle{ A }[/math] to the diagonal matrix with the same diagonal entries as [math]\displaystyle{ A. }[/math] The set [math]\displaystyle{ \mathcal{O}_{\tilde{\lambda}} }[/math] is a Hamiltonian [math]\displaystyle{ \mathbb{T} }[/math]-manifold, and the restriction of [math]\displaystyle{ \Phi }[/math] to this set is a moment map for this action.
By the Atiyah–Guillemin–Sternberg theorem, [math]\displaystyle{ \Phi(\mathcal{O}_{\tilde{\lambda}}) }[/math] is a convex polytope. A matrix [math]\displaystyle{ A \in \mathcal{H}(n) }[/math] is fixed under conjugation by every element of [math]\displaystyle{ \mathbb{T} }[/math] if and only if [math]\displaystyle{ A }[/math] is diagonal. The only diagonal matrices in [math]\displaystyle{ \mathcal{O}_{\tilde{\lambda}} }[/math] are the ones with diagonal entries [math]\displaystyle{ \lambda_1, \lambda_2, \ldots, \lambda_n }[/math] in some order. Thus, these matrices generate the convex polytope [math]\displaystyle{ \Phi(\mathcal{O}_{\tilde{\lambda}}). }[/math] This is exactly the statement of the Schur–Horn theorem.
Notes
References
- Schur, Issai, Über eine Klasse von Mittelbildungen mit Anwendungen auf die Determinantentheorie, Sitzungsber. Berl. Math. Ges. 22 (1923), 9–20.
- Horn, Alfred, Doubly stochastic matrices and the diagonal of a rotation matrix, American Journal of Mathematics 76 (1954), 620–630.
- Kadison, R. V.; Pedersen, G. K., Means and Convex Combinations of Unitary Operators, Math. Scand. 57 (1985),249–266.
- Kadison, R. V., The Pythagorean Theorem: I. The finite case, Proc. Natl. Acad. Sci. USA, vol. 99 no. 7 (2002):4178–4184 (electronic)
External links
- MathWorld
- Terry Tao: 254A, Notes 3a: Eigenvalues and sums of Hermitian matrices
- Sheela Devadas, Peter J. Haine, Keaton Stubis: The Schur-Horn Theorem
 |