Spillover (experiment)
In experiments, a spillover is an indirect effect on a subject not directly treated by the experiment. These effects are useful for policy analysis but complicate the statistical analysis of experiments. Analysis of spillover effects involves relaxing the non-interference assumption, or SUTVA (Stable Unit Treatment Value Assumption). This assumption requires that subject i's revelation of its potential outcomes depends only on that subject i's own treatment status, and is unaffected by another subject j's treatment status. In ordinary settings where the researcher seeks to estimate the average treatment effect (), violation of the non-interference assumption means that traditional estimators for the ATE, such as difference-in-means, may be biased. However, there are many real-world instances where a unit's revelation of potential outcomes depend on another unit's treatment assignment, and analyzing these effects may be just as important as analyzing the direct effect of treatment.
One solution to this problem is to redefine the causal estimand of interest by redefining a subject's potential outcomes in terms of one's own treatment status and related subjects' treatment status. The researcher can then analyze various estimands of interest separately. One important assumption here is that this process captures all patterns of spillovers, and that there are no unmodeled spillovers remaining (ex. spillovers occur within a two-person household but not beyond).
Once the potential outcomes are redefined, the rest of the statistical analysis involves modeling the probabilities of being exposed to treatment given some schedule of treatment assignment, and using inverse probability weighting (IPW) to produce unbiased (or asymptotically unbiased) estimates of the estimand of interest.
Examples of spillover effects
Spillover effects can occur in a variety of different ways. Common applications include the analysis of social network spillovers and geographic spillovers. Examples include the following:
- Communication: An intervention that conveys information about a technology or product can influence the take-up decisions of others in their network if it diffuses beyond the initial user.[1]
- Competition: Job placement assistance for young job seekers may influence the job market prospects of individuals who did not receive the training but are competing for the same jobs.[2]
- Contagion: Receiving deworming drugs can decrease other's likelihood of contracting the disease.[3]
- Deterrence: Information about government audits in specific municipalities can spread to nearby municipalities.[4]
- Displacement: A hotspot policing intervention that increases policing presence on a given street can lead to the displacement of crime onto nearby untreated streets.[5]
- Reallocation of resources: A hotspot policing intervention that increases policing presence on a given street can decrease police presence on nearby streets.
- Social comparison: A program that randomizes individuals to receive a voucher to move to a new neighborhood can additionally influence the control group's beliefs about their housing conditions.[6]
In such examples, treatment in a randomized-control trial can have a direct effect on those who receive the intervention and also a spillover effect on those who were not directly treated.
Statistical issues
Estimating spillover effects in experiments introduces three statistical issues that researchers must take into account.
Relaxing the non-interference assumption
One key assumption for unbiased inference is the non-interference assumption, which posits that an individual's potential outcomes are only revealed by their own treatment assignment and not the treatment assignment of others.[7] This assumption has also been called the Individualistic Treatment Response[8] or the stable unit treatment value assumption. Non-interference is violated when subjects can communicate with each other about their treatments, decisions, or experiences, thereby influencing each other's potential outcomes. If the non-interference assumption does not hold, units no longer have just two potential outcomes (treated and control), but a variety of other potential outcomes that depend on other units’ treatment assignments,[9] which complicates the estimation of the average treatment effect.
Estimating spillover effects requires relaxing the non-interference assumption. This is because a unit's outcomes depend not only on its treatment assignment but also on the treatment assignment of its neighbors. The researcher must posit a set of potential outcomes that limit the type of interference. As an example, consider an experiment that sends out political information to undergraduate students to increase their political participation. If the study population consists of all students living with a roommate in a college dormitory, one can imagine four sets of potential outcomes, depending on whether the student or their partner received the information (assume no spillover outside of each two-person room):
- Y0,0 refers to an individual's potential outcomes when they are not treated (0) and neither was their roommate (0).
- Y0,1 refers to an individual's potential outcome when they are not treated (0) but their roommate was treated (1).
- Y1,0 refers to an individual's potential outcome when they are treated (1) but their roommate was not treated (0).
- Y1,1 refers to an individual's potential outcome when they are treated (1) and their roommate was treated (1).
Now an individual's outcomes are influenced by both whether they received the treatment and whether their roommate received the treatment. We can estimate one type of spillover effect by looking at how one's outcomes change depending on whether their roommate received the treatment or not, given the individual did not receive treatment directly. This would be captured by the difference Y0,1- Y0,0. Similarly, we can measure how ones’ outcomes change depending on their roommate's treatment status, when the individual themselves are treated. This amounts to taking the difference Y1,1- Y1,0.
While researchers typically embrace experiments because they require less demanding assumptions, spillovers can be “unlimited in extent and impossible to specify in form.” [10] The researcher must make specific assumptions about which types of spillovers are operative. One can relax the non-interference assumption in various ways depending on how spillovers are thought to occur in a given setting. One way to model spillover effects is a binary indicator for whether an immediate neighbor was also treated, as in the example above. One can also posit spillover effects that depend on the number of immediate neighbors that were also treated, also known as k-level effects.[11]
Exposure mappings
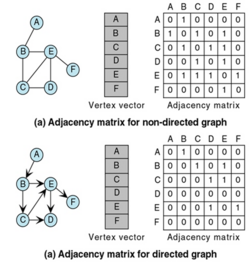
The next step after redefining the causal estimand of interest is to characterize the probability of spillover exposure for each subject in the analysis, given some vector of treatment assignment. Aronow and Samii (2017)[12] present a method for obtaining a matrix of exposure probabilities for each unit in the analysis.
First, define a diagonal matrix with a vector of treatment assignment probabilities
Second, define an indicator matrix of whether the unit is exposed to spillover or not. This is done by using an adjacency matrix as shown on the right, where information regarding a network can be transformed into an indicator matrix. This resulting indicator matrix will contain values of , the realized values of a random binary variable , indicating whether that unit has been exposed to spillover or not.
Third, obtain the sandwich product , an N × N matrix which contains two elements: the individual probability of exposure on the diagonal, and the joint exposure probabilities on the off diagonals:
- In a similar fashion, the joint probability of exposure of i being in exposure condition and j being in a different exposure condition can be obtained by calculating :
Notice that the diagonals on the second matrix are 0 because a subject cannot be simultaneously exposed to two different exposure conditions at once, in the same way that a subject cannot reveal two different potential outcomes at once.
The obtained exposure probabilities then can be used for inverse probability weighting (IPW, described below), in an estimator such as the Horvitz–Thompson estimator.
One important caveat is that this procedure excludes all units whose probability of exposure is zero (ex. a unit that is not connected to any other units), since these numbers end up in the denominator of the IPW regression.
Need for inverse probability weights
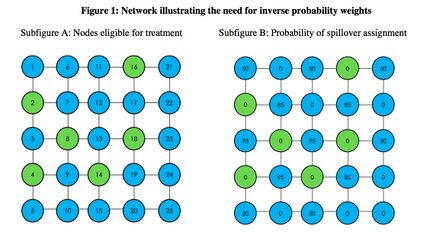
Estimating spillover effects requires additional care: although treatment is directly assigned, spillover status is indirectly assigned and can lead to differential probabilities of spillover assignment for units. For example, a subject with 10 friend connections is more likely to be indirectly exposed to treatment as opposed to a subject with just one friend connection. Not accounting for varying probabilities of spillover exposure can bias estimates of the average spillover effect.
Figure 1 displays an example where units have varying probabilities of being assigned to the spillover condition. Subfigure A displays a network of 25 nodes where the units in green are eligible to receive treatment. Spillovers are defined as sharing at least one edge with a treated unit. For example, if node 16 is treated, nodes 11, 17, and 21 would be classified as spillover units. Suppose three of these six green units are selected randomly to be treated, so that different sets of treatment assignments are possible. In this case, subfigure B displays each node's probability of being assigned to the spillover condition. Node 3 is assigned to spillover in 95% of the randomizations because it shares edges with three units that are treated. This node will only be a control node in 5% of randomizations: that is, when the three treated nodes are 14, 16, and 18. Meanwhile, node 15 is assigned to spillover only 50% of the time—if node 14 is not directly treated, node 15 will not be assigned to spillover.
Using inverse probability weights
When analyzing experiments with varying probabilities of assignment, special precautions should be taken. These differences in assignment probabilities may be neutralized by inverse-probability-weighted (IPW) regression, where each observation is weighted by the inverse of its likelihood of being assigned to the treatment condition observed using the Horvitz-Thompson estimator.[13] This approach addresses the bias that might arise if potential outcomes were systematically related to assignment probabilities. The downside of this estimator is that it may be fraught with sampling variability if some observations are accorded a high amount of weight (i.e. a unit with a low probability of being spillover is assigned to the spillover condition by chance).
Using randomization inference for hypothesis testing
In some settings, estimating the variability of a spillover effect creates additional difficulty. When the research study has a fixed unit of clustering, such as a school or household, researchers can use traditional standard error adjustment tools like cluster-robust standard errors, which allow for correlations in error terms within clusters but not across them.[14] In other settings, however, there is no fixed unit of clustering. In order to conduct hypothesis testing in these settings, the use of randomization inference is recommended.[15] This technique allows one to generate p-values and confidence intervals even when spillovers do not adhere to a fixed unit of clustering but nearby units tend to be assigned to similar spillover conditions, as in the case of fuzzy clustering.
See also
References
- ↑ "Diffusion of Technologies within Social Networks: Evidence from a Coffee Training Program in Rwanda" (in en-GB). 31 March 2010. https://www.theigc.org/project/diffusion-of-technologies-within-social-networks-evidence-from-a-coffee-training-program-in-rwanda/.
- ↑ Zamora, Philippe; Rathelot, Roland; Gurgand, Marc; Duflo, Esther; Crépon, Bruno (2013-05-01). "Do Labor Market Policies have Displacement Effects? Evidence from a Clustered Randomized Experiment" (in en). The Quarterly Journal of Economics 128 (2): 531–580. doi:10.1093/qje/qjt001. ISSN 0033-5533.
- ↑ "Worms: Identifying Impacts on Education and Health in the Presence of Treatment Externalities | Edward Miguel, Professor of Economics, University of California, Berkeley". http://emiguel.econ.berkeley.edu/research/worms-identifying-impacts-on-education-and-health-in-the-presence-of-treatment-externalities.
- ↑ Avis, Eric; Ferraz, Claudio; Finan, Frederico (2018). "Do Government Audits Reduce Corruption? Estimating the Impacts of Exposing Corrupt Politicians". Journal of Political Economy 126 (5): 1912–1964. doi:10.1086/699209. http://www.nber.org/papers/w22443.pdf.
- ↑ Weisburd, David; Telep, Cody W. (2014-05-01). "Hot Spots Policing: What We Know and What We Need to Know" (in en). Journal of Contemporary Criminal Justice 30 (2): 200–220. doi:10.1177/1043986214525083. ISSN 1043-9862.
- ↑ Sobel, Michael (2006). "What do randomized studies of housing mobility demonstrate?". Journal of the American Statistical Association 101 (476): 1398–1407. doi:10.1198/016214506000000636.
- ↑ "PsycNET" (in en). http://psycnet.apa.org/record/1959-07233-000.
- ↑ Manski, Charles F. (2013-02-01). "Identification of treatment response with social interactions" (in en). The Econometrics Journal 16 (1): S1–S23. doi:10.1111/j.1368-423X.2012.00368.x. ISSN 1368-4221. http://cemmap.ifs.org.uk/wps/cwp0110-2.pdf.
- ↑ Rosenbaum, Paul R. (2007). "Interference Between Units in Randomized Experiments". Journal of the American Statistical Association 102 (477): 191–200. doi:10.1198/016214506000001112.
- ↑ Rosenbaum, Paul R. (2007). "Interference Between Units in Randomized Experiments". Journal of the American Statistical Association 102 (477): 191–200. doi:10.1198/016214506000001112.
- ↑ Kao, Edward; Toulis, Panos (2013-02-13). "Estimation of Causal Peer Influence Effects" (in en). International Conference on Machine Learning: 1489–1497. http://proceedings.mlr.press/v28/toulis13.html.
- ↑ Aronow, Peter M.; Samii, Cyrus (2017-12-01). "Estimating average causal effects under general interference, with application to a social network experiment". The Annals of Applied Statistics 11 (4): 1912–1947. doi:10.1214/16-aoas1005. ISSN 1932-6157.
- ↑ Hortvitz, D. G.; Thompson, D. J. (1952). "A generalization of sampling without replacement from a finite universe". Journal of the American Statistical Association 47 (260): 663–685. doi:10.1080/01621459.1952.10483446.
- ↑ "A Practitioner's Guide to Cluster-Robust Inference". http://cameron.econ.ucdavis.edu/research/Cameron_Miller_JHR_2015_February.pdf. Retrieved 19 December 2018.
- ↑ "10 Things to Know About Randomization Inference". https://egap.org/methods-guides/10-things-randomization-inference.
 |
