Vortex theory of the atom

Short description: Incorrect but seminal physical theory

The vortex theory of the atom was a 19th-century attempt by William Thomson (later Lord Kelvin) to explain why the atoms recently discovered by chemists came in only relatively few varieties but in very great numbers of each kind. Based on the idea of stable, knotted vortices in the ether or aether, it contributed an important mathematical legacy.

Description

A vortex ring with a smoke-filled core.

The vortex theory of the atom was based on the observation that a stable vortex can be created in a fluid by making it into a ring with no ends. Such vortices could be sustained in the luminiferous aether, a hypothetical fluid thought at the time to pervade all of space. In the vortex theory of the atom, a chemical atom is modelled by such a vortex in the aether.

Knots can be tied in the core of such a vortex, leading to the hypothesis that each chemical element corresponds to a different kind of knot. The simple toroidal vortex, represented by the circular "unknot" 0₁, was thought to represent hydrogen. Many elements had yet to be discovered, so the next knot, the trefoil knot 3₁, was thought to represent carbon.

However, as more elements were discovered and the periodicity of their characteristics established in the periodic table of the elements, it became clear that this could not be explained by any rational classification of knots. This, together with the discovery of subatomic particles such as the electron, led to the theory being abandoned.

History

Between 1870 and 1890 the vortex atom theory, which hypothesised that an atom was a vortex in the aether, was popular among British physicists and mathematicians. William Thomson, who became better known as Lord Kelvin, first conjectured that atoms might be vortices in the aether that pervades space. About 60 scientific papers were subsequently written on it by approximately 25 scientists.

Origins

In the seventeenth century Descartes developed a theory of vortex motion to explain such things as why light radiated in all directions and the planets moved in circular orbits. He believed that there was no vacuum and any object which moved had to be entering a gap left by another moving object. He realised that a circular chain of such objects, all replacing each other, would enable such movement. Thus, all movement consisted of endless circular vortices at all scales. However his Treatise on Light remained unfinished.

Hermann Helmholtz realized in the mid-19th century that the core of a vortex, analogous to the eye of a hurricane, is a line-like filament that can become tangled up with other filaments in a knotted loop that cannot come undone. It is not necessary for the core to circulate, as it did in the Cartesian model. Helmholtz also showed that vortices exert forces on one another, and those forces take a form analogous to the magnetic forces between electrical wires.

During the intervening period, chemist John Dalton had developed his atomic theory of matter. It remained only to bring the two strands of discovery together.

William Thomson (Lord Kelvin)

William Thomson, later to become Lord Kelvin, became concerned with the nature of Dalton's chemical elements, whose atoms appeared in only a few forms but in vast numbers. He was inspired by Helmholtz's findings, reasoning that the aether, a substance then hypothesised to pervade all of space, should be capable of supporting such stable vortices. According to Helmholtz’s theorems, these vortices would correspond to different kinds of knot. Thomson suggested that each type of knot might represent an atom of a different chemical element. He further speculated that multiple knots might aggregate into molecules of somewhat lower stability.

He published his paper "On Vortex Atoms" in the Proceedings of the Royal Society of Edinburgh in 1867.

Peter Tait

The knots with up to 7 crossings.

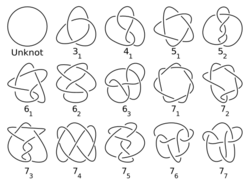
Thomson's colleague Peter Guthrie Tait was attracted by the vortex atom theory and undertook a pioneering study of knots, producing a systematic classification of those with up to 10 crossings, in the hope of thus systematizing the various elements.

J. J. Thomson

J. J. Thomson took up the challenge in his 1883 Master's degree thesis, a Treatise on the motion of vortex rings. In it, Thomson developed a mathematical treatment of the motions of William Thomson and Peter Tait's atoms.

When Thomson later discovered the electron (for which he received a Nobel Prize), he abandoned his "nebular atom" hypothesis based on the vortex atomic theory, in favour of his plum pudding model.

Legacy

Tait's work especially founded the branch of topology called knot theory, with J. J. Thomson providing some early mathematical advancements.

Kelvin's insight continues to inspire new mathematics and has led to persistence of the topic in the history of science.

See also

• Loop quantum gravity
• Magnetic skyrmion, a vortex-like magnetic quasiparticle
• Quantum vortex, a quantised flux circulation
• Toroidal ring model of elementary particles

References

Bibliography

• Kragh, Helge (2002). "The Vortex Atom: A Victorian Theory of Everything" (in en). Centaurus 44 (1–2): 32–114. doi:10.1034/j.1600-0498.2002.440102.x. ISSN 0008-8994. https://www.academia.edu/4084776. Retrieved 9 March 2019. </ref>