Physics:Furry's theorem

Short description: Theorem in quantum physics

This triangle diagram is forbidden by Furry's theorem in quantum electrodynamics.

In quantum electrodynamics, Furry's theorem states that if a Feynman diagram consists of a closed loop of fermion lines with an odd number of vertices, its contribution to the amplitude vanishes. As a corollary, a single photon cannot arise from the vacuum or be absorbed by it. The theorem was first derived by Wendell H. Furry in 1937, as a direct consequence of the conservation of energy and charge conjugation symmetry.

Theory

Quantum electrodynamics has a number of symmetries, one of them being the discrete symmetry of charge conjugation. This acts on fields through a unitary charge conjugation operator [math]\displaystyle{ C }[/math] which anticommutes with the photon field [math]\displaystyle{ A_\mu(x) }[/math] as [math]\displaystyle{ CA^\mu(x) C^\dagger = -A^\mu(x) }[/math], while leaving the vacuum state invariant [math]\displaystyle{ C|\Omega\rangle = |\Omega\rangle }[/math]. Considering the simplest case of the correlation function of a single photon operator gives

[math]\displaystyle{ \langle \Omega|A^\mu(x)|\Omega\rangle = \langle \Omega|C^\dagger C A^\mu(x) C^\dagger C|\Omega\rangle = - \langle \Omega|A^\mu(x)|\Omega\rangle, }[/math]

so this correlation function must vanish. For [math]\displaystyle{ n }[/math] photon operators, this argument shows that under charge conjugation this picks up a factor of [math]\displaystyle{ (-1)^n }[/math] and thus vanishes when [math]\displaystyle{ n }[/math] is odd. More generally, since the charge conjugation operator also anticommutes with the vector current [math]\displaystyle{ j^\mu(x) }[/math], Furry's theorem states that the correlation function of any odd number of on-shell or off-shell photon fields and/or currents must vanish in quantum electrodynamics.

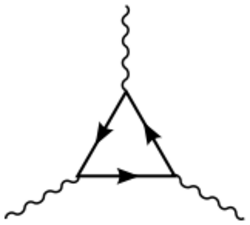
Since the theorem holds at the non-perturbative level, it must also hold at each order in perturbation theory. At leading order this means that any fermion loop with an odd number of vertices must have a vanishing contribution to the amplitude. An explicit calculation of these diagrams reveals that this is because the diagram with a fermion going clockwise around the loop cancels with the second diagram where the fermion goes anticlockwise. The vanishing of the three vertex loop can also be seen as a consequence of the renormalizability of quantum electrodynamics since the bare Lagrangian does not have any counterterms involving three photons.

Applications and limitations

Furry's theorem allows for the simplification of a number of amplitude calculations in quantum electrodynamics. In particular, since the result also holds when photons are off-shell, all Feynman diagrams which have at least one internal fermion loops with an odd number of vertices have a vanishing contribution to the amplitude and can be ignored. Historically the theorem was important in showing that the scattering of photons by an external field, known as Delbrück scattering, does not proceed via a triangle diagram and must instead proceed through a box diagram.

In the presence of a background charge density or a nonzero chemical potential, Furry's theorem is broken, although if both these vanish then it does hold at nonzero temperatures as well as at zero temperatures. It also does not apply in the presence of a strong background magnetic field where photon splitting interactions [math]\displaystyle{ \gamma \rightarrow \gamma \gamma }[/math] are allowed, a process that may be detected in astrophysical settings such as around neutron stars. The theorem also does not hold when Weyl fermions are involved in the loops rather than Dirac fermions, resulting in non-vanishing odd vertex number diagrams. In particular, the non-vanishing of the triangle diagram with Weyl fermions gives rise to the chiral anomaly, with the sum of these having to cancel for a quantum theory to be consistent.

While the theorem has been formulated in quantum electrodynamics, a version of it holds more generally. For example, while the Standard Model is not charge conjugation invariant due to weak interactions, the fermion loop diagrams with an odd number of photons attached will still vanish since these are equivalent to a purely quantum electrodynamical diagram. Similarly, any diagram involving such loops as sub-diagrams will also vanish. It is however no longer true that all odd number photon diagrams need to vanish. For example, relaxing the requirement of charge conjugation and parity invariance of quantum electrodynamics, as occurs when weak interactions are included, allows for a three-photon vertex term. While this term does give rise to [math]\displaystyle{ \gamma \rightarrow \gamma \gamma }[/math] interactions, they only occur if two of the photons are virtual; searching for such interactions must be done indirectly, such as through bremsstrahlung experiments from electron-positron collisions.

In non-Abelian Yang–Mills theories, Furry's theorem does not hold since these involve noncommuting color charges. For example, the quark triangle diagrams with three external gluons are proportional to two different generator traces [math]\displaystyle{ \text{tr}[T^aT^bT^c] \neq \text{tr}[T^aT^cT^b] }[/math] and so they do not cancel. However, charge conjugation arguments can still be applied in limited cases such as to deduce that the triangle diagram [math]\displaystyle{ gg \rightarrow X }[/math] for a color neutral spin [math]\displaystyle{ 1^- }[/math] boson vanishes.

See also

• Landau–Yang theorem
• Ward–Takahashi identity
• Wick's theorem