Physics:Coriolis force
| Part of a series on |
| Classical mechanics |
|---|
| [math]\displaystyle{ \textbf{F} = \frac{d}{dt} (m\textbf{v}) }[/math] |

In physics, the Coriolis force is an inertial (or fictitious) force that acts on objects in motion within a frame of reference that rotates with respect to an inertial frame. In a reference frame with clockwise rotation, the force acts to the left of the motion of the object. In one with anticlockwise (or counterclockwise) rotation, the force acts to the right. Deflection of an object due to the Coriolis force is called the Coriolis effect. Though recognized previously by others, the mathematical expression for the Coriolis force appeared in an 1835 paper by French scientist Gaspard-Gustave de Coriolis, in connection with the theory of water wheels. Early in the 20th century, the term Coriolis force began to be used in connection with meteorology.
Newton's laws of motion describe the motion of an object in an inertial (non-accelerating) frame of reference. When Newton's laws are transformed to a rotating frame of reference, the Coriolis and centrifugal accelerations appear. When applied to objects with masses, the respective forces are proportional to their masses. The magnitude of the Coriolis force is proportional to the rotation rate, and the magnitude of the centrifugal force is proportional to the square of the rotation rate. The Coriolis force acts in a direction perpendicular to two quantities: the angular velocity of the rotating frame relative to the inertial frame and the velocity of the body relative to the rotating frame, and its magnitude is proportional to the object's speed in the rotating frame (more precisely, to the component of its velocity that is perpendicular to the axis of rotation). The centrifugal force acts outwards in the radial direction and is proportional to the distance of the body from the axis of the rotating frame. These additional forces are termed inertial forces, fictitious forces, or pseudo forces. By introducing these fictitious forces to a rotating frame of reference, Newton's laws of motion can be applied to the rotating system as though it were an inertial system; these forces are correction factors that are not required in a non-rotating system.
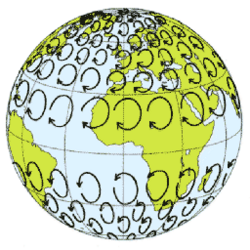
In popular (non-technical) usage of the term "Coriolis effect", the rotating reference frame implied is almost always the Earth. Because the Earth spins, Earth-bound observers need to account for the Coriolis force to correctly analyze the motion of objects. The Earth completes one rotation for each day/night cycle, so for motions of everyday objects the Coriolis force is imperceptible; its effects become noticeable only for motions occurring over large distances and long periods of time, such as large-scale movement of air in the atmosphere or water in the ocean; or where high precision is important, such as long-range artillery or missile trajectories. Such motions are constrained by the surface of the Earth, so only the horizontal component of the Coriolis force is generally important. This force causes moving objects on the surface of the Earth to be deflected to the right (with respect to the direction of travel) in the Northern Hemisphere and to the left in the Southern Hemisphere. The horizontal deflection effect is greater near the poles, since the effective rotation rate about a local vertical axis is largest there, and decreases to zero at the equator. Rather than flowing directly from areas of high pressure to low pressure, as they would in a non-rotating system, winds and currents tend to flow to the right of this direction north of the equator ("clockwise") and to the left of this direction south of it ("anticlockwise"). This effect is responsible for the rotation and thus formation of cyclones (see Coriolis effects in meteorology).
History
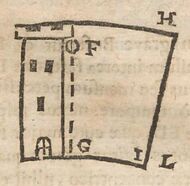
Italian scientist Giovanni Battista Riccioli and his assistant Francesco Maria Grimaldi described the effect in connection with artillery in the 1651 Almagestum Novum, writing that rotation of the Earth should cause a cannonball fired to the north to deflect to the east.[2] In 1674, Claude François Milliet Dechales described in his Cursus seu Mundus Mathematicus how the rotation of the Earth should cause a deflection in the trajectories of both falling bodies and projectiles aimed toward one of the planet's poles. Riccioli, Grimaldi, and Dechales all described the effect as part of an argument against the heliocentric system of Copernicus. In other words, they argued that the Earth's rotation should create the effect, and so failure to detect the effect was evidence for an immobile Earth.[3] The Coriolis acceleration equation was derived by Euler in 1749,[4][5] and the effect was described in the tidal equations of Pierre-Simon Laplace in 1778.[6]
Gaspard-Gustave Coriolis published a paper in 1835 on the energy yield of machines with rotating parts, such as waterwheels.[7][8] That paper considered the supplementary forces that are detected in a rotating frame of reference. Coriolis divided these supplementary forces into two categories. The second category contained a force that arises from the cross product of the angular velocity of a coordinate system and the projection of a particle's velocity into a plane perpendicular to the system's axis of rotation. Coriolis referred to this force as the "compound centrifugal force" due to its analogies with the centrifugal force already considered in category one.[9][10] The effect was known in the early 20th century as the "acceleration of Coriolis",[11] and by 1920 as "Coriolis force".[12]
In 1856, William Ferrel proposed the existence of a circulation cell in the mid-latitudes with air being deflected by the Coriolis force to create the prevailing westerly winds.[13]
The understanding of the kinematics of how exactly the rotation of the Earth affects airflow was partial at first.[14] Late in the 19th century, the full extent of the large scale interaction of pressure-gradient force and deflecting force that in the end causes air masses to move along isobars was understood.[15]
Formula
In Newtonian mechanics, the equation of motion for an object in an inertial reference frame is:
- [math]\displaystyle{ \boldsymbol{F} = m\boldsymbol{a} }[/math]
where [math]\displaystyle{ \boldsymbol{F} }[/math] is the vector sum of the physical forces acting on the object, [math]\displaystyle{ m }[/math] is the mass of the object, and [math]\displaystyle{ \boldsymbol{a} }[/math] is the acceleration of the object relative to the inertial reference frame.
Transforming this equation to a reference frame rotating about a fixed axis through the origin with angular velocity [math]\displaystyle{ \boldsymbol{\omega} }[/math] having variable rotation rate, the equation takes the form:[8][16]
- [math]\displaystyle{ \begin{align} \boldsymbol{F'} &= \boldsymbol{F} - m\frac{\mathrm{d} \boldsymbol{\omega}}{\mathrm{d}t}\times\boldsymbol{r'} - 2m \boldsymbol{\omega}\times \boldsymbol{v'} - m\boldsymbol{\omega} \times (\boldsymbol{\omega} \times \boldsymbol{r'}) \\ & = m\boldsymbol{a'} \end{align} }[/math]
where
- [math]\displaystyle{ \boldsymbol{F} }[/math] is the vector sum of the physical forces acting on the object
- [math]\displaystyle{ \boldsymbol{\omega} }[/math] is the angular velocity, of the rotating reference frame relative to the inertial frame
- [math]\displaystyle{ \boldsymbol{r'} }[/math] is the position vector of the object relative to the rotating reference frame
- [math]\displaystyle{ \boldsymbol{v'} }[/math] is the velocity of the object relative to the rotating reference frame
- [math]\displaystyle{ \boldsymbol{a'} }[/math] is the acceleration of the object relative to the rotating reference frame
The fictitious forces as they are perceived in the rotating frame act as additional forces that contribute to the apparent acceleration just like the real external forces.[17][18][19] The fictitious force terms of the equation are, reading from left to right:[20]
- Euler force, [math]\displaystyle{ -m \frac{\mathrm{d}\boldsymbol{\omega}}{\mathrm{d}t} \times\boldsymbol{r'} }[/math]
- Coriolis force, [math]\displaystyle{ -2m ( \boldsymbol{\omega} \times \boldsymbol{v'} ) }[/math]
- centrifugal force, [math]\displaystyle{ -m\boldsymbol{\omega} \times (\boldsymbol{\omega} \times \boldsymbol{r'}) }[/math]
As seen in these formulas the Euler and centrifugal forces depend on the position vector [math]\displaystyle{ \boldsymbol{r'} }[/math] of the object, while the Coriolis force depends on the object's velocity [math]\displaystyle{ \boldsymbol{v'} }[/math] as measured in the rotating reference frame. As expected, for a non-rotating inertial frame of reference [math]\displaystyle{ (\boldsymbol\omega=0) }[/math] the Coriolis force and all other fictitious forces disappear.[21]
Corollaries
As the Coriolis force is proportional to a cross product of two vectors, it is perpendicular to both vectors, in this case the object's velocity and the frame's rotation vector. It therefore follows that:
- if the velocity is parallel to the rotation axis, the Coriolis force is zero. For example, on Earth, this situation occurs for a body at the equator moving north or south relative to the Earth's surface.
- if the velocity is straight inward to the axis, the Coriolis force is in the direction of local rotation. For example, on Earth, this situation occurs for a body at the equator falling downward, as in the Dechales illustration above, where the falling ball travels further to the east than does the tower.
- if the velocity is straight outward from the axis, the Coriolis force is against the direction of local rotation. In the tower example, a ball launched upward would move toward the west.
- if the velocity is in the direction of rotation, the Coriolis force is outward from the axis. For example, on Earth, this situation occurs for a body at the equator moving east relative to Earth's surface. It would move upward as seen by an observer on the surface. This effect (see Eötvös effect below) was discussed by Galileo Galilei in 1632 and by Riccioli in 1651.[22]
- if the velocity is against the direction of rotation, the Coriolis force is inward to the axis. For example, on Earth, this situation occurs for a body at the equator moving west, which would deflect downward as seen by an observer.
Intuitive explanation
For an intuitive explanation of the origin of the Coriolis force, consider an object, constrained to follow the Earth's surface and moving northward in the Northern Hemisphere. Viewed from outer space, the object does not appear to go due north, but has an eastward motion (it rotates around toward the right along with the surface of the Earth). The further north it travels, the smaller the "radius of its parallel (latitude)" (the minimum distance from the surface point to the axis of rotation, which is in a plane orthogonal to the axis), and so the slower the eastward motion of its surface. As the object moves north, to higher latitudes, it has a tendency to maintain the eastward speed it started with (rather than slowing down to match the reduced eastward speed of local objects on the Earth's surface), so it veers east (i.e. to the right of its initial motion).[23][24]
Though not obvious from this example, which considers northward motion, the horizontal deflection occurs equally for objects moving eastward or westward (or in any other direction).[25] However, the theory that the effect determines the rotation of draining water in a typical size household bathtub, sink or toilet has been repeatedly disproven by modern-day scientists; the force is negligibly small compared to the many other influences on the rotation.[26][27][28]
Length scales and the Rossby number
The time, space, and velocity scales are important in determining the importance of the Coriolis force. Whether rotation is important in a system can be determined by its Rossby number, which is the ratio of the velocity, U, of a system to the product of the Coriolis parameter, [math]\displaystyle{ f = 2 \omega \sin \varphi \, }[/math], and the length scale, L, of the motion:
- [math]\displaystyle{ Ro = \frac{U}{fL}. }[/math]
Hence, it is the ratio of inertial to Coriolis forces; a small Rossby number indicates a system is strongly affected by Coriolis forces, and a large Rossby number indicates a system in which inertial forces dominate. For example, in tornadoes, the Rossby number is large, so in them the Coriolis force is negligible, and balance is between pressure and centrifugal forces. In low-pressure systems the Rossby number is low, as the centrifugal force is negligible; there, the balance is between Coriolis and pressure forces. In oceanic systems the Rossby number is often around 1, with all three forces comparable.[29]
An atmospheric system moving at U = 10 m/s (22 mph) occupying a spatial distance of L = 1,000 km (621 mi), has a Rossby number of approximately 0.1.[citation needed]
A baseball pitcher may throw the ball at U = 45 m/s (100 mph) for a distance of L = 18.3 m (60 ft). The Rossby number in this case would be 32,000 (at latitude 31°47'46.382").[citation needed]
Baseball players don't care about which hemisphere they're playing in. However, an unguided missile obeys exactly the same physics as a baseball, but can travel far enough and be in the air long enough to experience the effect of Coriolis force. Long-range shells in the Northern Hemisphere landed close to, but to the right of, where they were aimed until this was noted. (Those fired in the Southern Hemisphere landed to the left.) In fact, it was this effect that first got the attention of Coriolis himself.[30][31][32]
Simple cases
Tossed ball on a rotating carousel
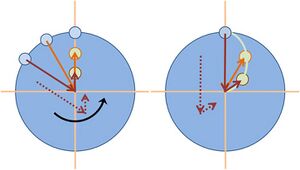
The figure illustrates a ball tossed from 12:00 o'clock toward the center of a counter-clockwise rotating carousel. On the left, the ball is seen by a stationary observer above the carousel, and the ball travels in a straight line to the center, while the ball-thrower rotates counter-clockwise with the carousel. On the right, the ball is seen by an observer rotating with the carousel, so the ball-thrower appears to stay at 12:00 o'clock. The figure shows how the trajectory of the ball as seen by the rotating observer can be constructed.[citation needed]
On the left, two arrows locate the ball relative to the ball-thrower. One of these arrows is from the thrower to the center of the carousel (providing the ball-thrower's line of sight), and the other points from the center of the carousel to the ball. (This arrow gets shorter as the ball approaches the center.) A shifted version of the two arrows is shown dotted.[citation needed]
On the right is shown this same dotted pair of arrows, but now the pair are rigidly rotated so the arrow corresponding to the line of sight of the ball-thrower toward the center of the carousel is aligned with 12:00 o'clock. The other arrow of the pair locates the ball relative to the center of the carousel, providing the position of the ball as seen by the rotating observer. By following this procedure for several positions, the trajectory in the rotating frame of reference is established as shown by the curved path in the right-hand panel.[citation needed]
The ball travels in the air, and there is no net force upon it. To the stationary observer, the ball follows a straight-line path, so there is no problem squaring this trajectory with zero net force. However, the rotating observer sees a curved path. Kinematics insists that a force (pushing to the right of the instantaneous direction of travel for a counter-clockwise rotation) must be present to cause this curvature, so the rotating observer is forced to invoke a combination of centrifugal and Coriolis forces to provide the net force required to cause the curved trajectory.[citation needed]
Bounced ball
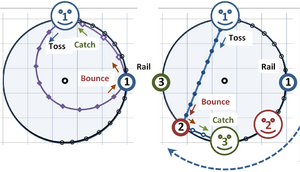
The figure describes a more complex situation where the tossed ball on a turntable bounces off the edge of the carousel and then returns to the tosser, who catches the ball. The effect of Coriolis force on its trajectory is shown again as seen by two observers: an observer (referred to as the "camera") that rotates with the carousel, and an inertial observer. The figure shows a bird's-eye view based upon the same ball speed on forward and return paths. Within each circle, plotted dots show the same time points. In the left panel, from the camera's viewpoint at the center of rotation, the tosser (smiley face) and the rail both are at fixed locations, and the ball makes a very considerable arc on its travel toward the rail, and takes a more direct route on the way back. From the ball tosser's viewpoint, the ball seems to return more quickly than it went (because the tosser is rotating toward the ball on the return flight).[citation needed]
On the carousel, instead of tossing the ball straight at a rail to bounce back, the tosser must throw the ball toward the right of the target and the ball then seems to the camera to bear continuously to the left of its direction of travel to hit the rail (left because the carousel is turning clockwise). The ball appears to bear to the left from direction of travel on both inward and return trajectories. The curved path demands this observer to recognize a leftward net force on the ball. (This force is "fictitious" because it disappears for a stationary observer, as is discussed shortly.) For some angles of launch, a path has portions where the trajectory is approximately radial, and Coriolis force is primarily responsible for the apparent deflection of the ball (centrifugal force is radial from the center of rotation, and causes little deflection on these segments). When a path curves away from radial, however, centrifugal force contributes significantly to deflection.[citation needed]
The ball's path through the air is straight when viewed by observers standing on the ground (right panel). In the right panel (stationary observer), the ball tosser (smiley face) is at 12 o'clock and the rail the ball bounces from is at position 1. From the inertial viewer's standpoint, positions 1, 2, and 3 are occupied in sequence. At position 2, the ball strikes the rail, and at position 3, the ball returns to the tosser. Straight-line paths are followed because the ball is in free flight, so this observer requires that no net force is applied.
Applied to the Earth
The acceleration affecting the motion of air "sliding" over the Earth's surface is the horizontal component of the Coriolis term
- [math]\displaystyle{ -2 \, \boldsymbol{\omega \times v} }[/math]
This component is orthogonal to the velocity over the Earth surface and is given by the expression
- [math]\displaystyle{ \omega \, v\ 2 \, \sin \phi }[/math]
where
- [math]\displaystyle{ \omega }[/math] is the spin rate of the Earth
- [math]\displaystyle{ \phi }[/math] is the latitude, positive in the northern hemisphere and negative in the southern hemisphere
In the northern hemisphere, where the latitude is positive, this acceleration, as viewed from above, is to the right of the direction of motion. Conversely, it is to the left in the southern hemisphere.
Rotating sphere
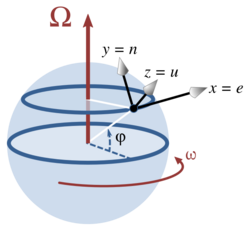
Consider a location with latitude φ on a sphere that is rotating around the north–south axis. A local coordinate system is set up with the x axis horizontally due east, the y axis horizontally due north and the z axis vertically upwards. The rotation vector, velocity of movement and Coriolis acceleration expressed in this local coordinate system (listing components in the order east (e), north (n) and upward (u)) are:[33]
- [math]\displaystyle{ \boldsymbol{ \Omega} = \omega \begin{pmatrix} 0 \\ \cos \varphi \\ \sin \varphi \end{pmatrix}\ , }[/math] [math]\displaystyle{ \boldsymbol{ v} = \begin{pmatrix} v_e \\ v_n \\ v_u \end{pmatrix}\ , }[/math]
- [math]\displaystyle{ \boldsymbol{ a}_C =-2\boldsymbol{\Omega \times v}= 2\,\omega\, \begin{pmatrix} v_n \sin \varphi-v_u \cos \varphi \\ -v_e \sin \varphi \\ v_e \cos\varphi\end{pmatrix}\ . }[/math]
When considering atmospheric or oceanic dynamics, the vertical velocity is small, and the vertical component of the Coriolis acceleration ([math]\displaystyle{ v_e \cos\varphi }[/math]) is small compared with the acceleration due to gravity (g, approximately 9.81 m/s2 (32.2 ft/s2) near Earth's surface). For such cases, only the horizontal (east and north) components matter.[citation needed] The restriction of the above to the horizontal plane is (setting vu = 0):[citation needed]
- [math]\displaystyle{ \boldsymbol{ v} = \begin{pmatrix} v_e \\ v_n\end{pmatrix}\ , }[/math] [math]\displaystyle{ \boldsymbol{ a}_c = \begin{pmatrix} v_n \\ -v_e\end{pmatrix}\ f\ , }[/math]
where [math]\displaystyle{ f = 2 \omega \sin \varphi \, }[/math] is called the Coriolis parameter.
By setting vn = 0, it can be seen immediately that (for positive φ and ω) a movement due east results in an acceleration due south; similarly, setting ve = 0, it is seen that a movement due north results in an acceleration due east.[citation needed] In general, observed horizontally, looking along the direction of the movement causing the acceleration, the acceleration always is turned 90° to the right (for positive φ) and of the same size regardless of the horizontal orientation.[citation needed]
In the case of equatorial motion, setting φ = 0° yields:
- [math]\displaystyle{ \boldsymbol{ \Omega} = \omega \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}\ , }[/math] [math]\displaystyle{ \boldsymbol{ v} = \begin{pmatrix} v_e \\ v_n \\ v_u \end{pmatrix}\ , }[/math] [math]\displaystyle{ \boldsymbol{ a}_C = -2\boldsymbol{\Omega \times v} = 2\,\omega\, \begin{pmatrix} -v_u \\0 \\ v_e \end{pmatrix}\ . }[/math]
Ω in this case is parallel to the north axis.
Accordingly, an eastward motion (that is, in the same direction as the rotation of the sphere) provides an upward acceleration known as the Eötvös effect, and an upward motion produces an acceleration due west.
Meteorology and oceanography
Perhaps the most important impact of the Coriolis effect is in the large-scale dynamics of the oceans and the atmosphere. In meteorology and oceanography, it is convenient to postulate a rotating frame of reference wherein the Earth is stationary. In accommodation of that provisional postulation, the centrifugal and Coriolis forces are introduced. Their relative importance is determined by the applicable Rossby numbers. Tornadoes have high Rossby numbers, so, while tornado-associated centrifugal forces are quite substantial, Coriolis forces associated with tornadoes are for practical purposes negligible.[34]
Because surface ocean currents are driven by the movement of wind over the water's surface, the Coriolis force also affects the movement of ocean currents and cyclones as well. Many of the ocean's largest currents circulate around warm, high-pressure areas called gyres. Though the circulation is not as significant as that in the air, the deflection caused by the Coriolis effect is what creates the spiralling pattern in these gyres. The spiralling wind pattern helps the hurricane form. The stronger the force from the Coriolis effect, the faster the wind spins and picks up additional energy, increasing the strength of the hurricane.[35][better source needed]
Air within high-pressure systems rotates in a direction such that the Coriolis force is directed radially inwards, and nearly balanced by the outwardly radial pressure gradient. As a result, air travels clockwise around high pressure in the Northern Hemisphere and anticlockwise in the Southern Hemisphere. Air around low-pressure rotates in the opposite direction, so that the Coriolis force is directed radially outward and nearly balances an inwardly radial pressure gradient.[36][better source needed]
Flow around a low-pressure area
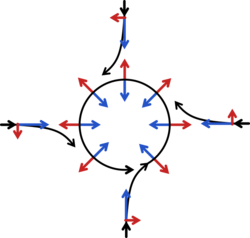
If a low-pressure area forms in the atmosphere, air tends to flow in towards it, but is deflected perpendicular to its velocity by the Coriolis force. A system of equilibrium can then establish itself creating circular movement, or a cyclonic flow. Because the Rossby number is low, the force balance is largely between the pressure-gradient force acting towards the low-pressure area and the Coriolis force acting away from the center of the low pressure.
Instead of flowing down the gradient, large scale motions in the atmosphere and ocean tend to occur perpendicular to the pressure gradient. This is known as geostrophic flow.[37] On a non-rotating planet, fluid would flow along the straightest possible line, quickly eliminating pressure gradients. The geostrophic balance is thus very different from the case of "inertial motions" (see below), which explains why mid-latitude cyclones are larger by an order of magnitude than inertial circle flow would be.[citation needed]
This pattern of deflection, and the direction of movement, is called Buys-Ballot's law. In the atmosphere, the pattern of flow is called a cyclone. In the Northern Hemisphere the direction of movement around a low-pressure area is anticlockwise. In the Southern Hemisphere, the direction of movement is clockwise because the rotational dynamics is a mirror image there.[38] At high altitudes, outward-spreading air rotates in the opposite direction.[citation needed][39][full citation needed] Cyclones rarely form along the equator due to the weak Coriolis effect present in this region.[40]
Inertial circles
An air or water mass moving with speed [math]\displaystyle{ v\, }[/math] subject only to the Coriolis force travels in a circular trajectory called an inertial circle. Since the force is directed at right angles to the motion of the particle, it moves with a constant speed around a circle whose radius [math]\displaystyle{ R }[/math] is given by:
- [math]\displaystyle{ R = \frac{v}{f} }[/math]
where [math]\displaystyle{ f }[/math] is the Coriolis parameter [math]\displaystyle{ 2 \Omega \sin \varphi }[/math], introduced above (where [math]\displaystyle{ \varphi }[/math] is the latitude). The time taken for the mass to complete a full circle is therefore [math]\displaystyle{ 2\pi/f }[/math]. The Coriolis parameter typically has a mid-latitude value of about 10−4 s−1; hence for a typical atmospheric speed of 10 m/s (22 mph), the radius is 100 km (62 mi) with a period of about 17 hours. For an ocean current with a typical speed of 10 cm/s (0.22 mph), the radius of an inertial circle is 1 km (0.6 mi). These inertial circles are clockwise in the northern hemisphere (where trajectories are bent to the right) and anticlockwise in the southern hemisphere.
If the rotating system is a parabolic turntable, then [math]\displaystyle{ f }[/math] is constant and the trajectories are exact circles. On a rotating planet, [math]\displaystyle{ f }[/math] varies with latitude and the paths of particles do not form exact circles. Since the parameter [math]\displaystyle{ f }[/math] varies as the sine of the latitude, the radius of the oscillations associated with a given speed are smallest at the poles (latitude of ±90°), and increase toward the equator.[41]
Other terrestrial effects
The Coriolis effect strongly affects the large-scale oceanic and atmospheric circulation, leading to the formation of robust features like jet streams and western boundary currents. Such features are in geostrophic balance, meaning that the Coriolis and pressure gradient forces balance each other. Coriolis acceleration is also responsible for the propagation of many types of waves in the ocean and atmosphere, including Rossby waves and Kelvin waves. It is also instrumental in the so-called Ekman dynamics in the ocean, and in the establishment of the large-scale ocean flow pattern called the Sverdrup balance.
Eötvös effect
The practical impact of the "Coriolis effect" is mostly caused by the horizontal acceleration component produced by horizontal motion.
There are other components of the Coriolis effect. Westward-traveling objects are deflected downwards, while eastward-traveling objects are deflected upwards.[42] This is known as the Eötvös effect. This aspect of the Coriolis effect is greatest near the equator. The force produced by the Eötvös effect is similar to the horizontal component, but the much larger vertical forces due to gravity and pressure suggest that it is unimportant in the hydrostatic equilibrium. However, in the atmosphere, winds are associated with small deviations of pressure from the hydrostatic equilibrium. In the tropical atmosphere, the order of magnitude of the pressure deviations is so small that the contribution of the Eötvös effect to the pressure deviations is considerable.[43]
In addition, objects traveling upwards (i.e. out) or downwards (i.e. in) are deflected to the west or east respectively. This effect is also the greatest near the equator. Since vertical movement is usually of limited extent and duration, the size of the effect is smaller and requires precise instruments to detect. For example, idealized numerical modeling studies suggest that this effect can directly affect tropical large-scale wind field by roughly 10% given long-duration (2 weeks or more) heating or cooling in the atmosphere.[44][45] Moreover, in the case of large changes of momentum, such as a spacecraft being launched into orbit, the effect becomes significant. The fastest and most fuel-efficient path to orbit is a launch from the equator that curves to a directly eastward heading.
Intuitive example
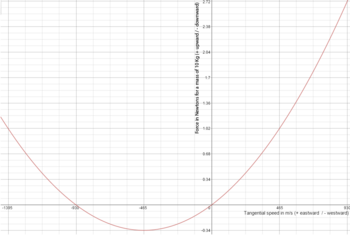
Imagine a train that travels through a frictionless railway line along the equator. Assume that, when in motion, it moves at the necessary speed to complete a trip around the world in one day (465 m/s).[46] The Coriolis effect can be considered in three cases: when the train travels west, when it is at rest, and when it travels east. In each case, the Coriolis effect can be calculated from the rotating frame of reference on Earth first, and then checked against a fixed inertial frame. The image below illustrates the three cases as viewed by an observer at rest in a (near) inertial frame from a fixed point above the North Pole along the Earth's axis of rotation; the train is denoted by a few red pixels, fixed at the left side in the leftmost picture, moving in the others [math]\displaystyle{ \left(1\text{ day} \mathrel\overset{\land}{=} 8\text{ s}\right): }[/math]
- The train travels toward the west: In that case, it moves against the direction of rotation. Therefore, on the Earth's rotating frame the Coriolis term is pointed inwards towards the axis of rotation (down). This additional force downwards should cause the train to be heavier while moving in that direction.If one looks at this train from the fixed non-rotating frame on top of the center of the Earth, at that speed it remains stationary as the Earth spins beneath it. Hence, the only force acting on it is gravity and the reaction from the track. This force is greater (by 0.34%)[46] than the force that the passengers and the train experience when at rest (rotating along with Earth). This difference is what the Coriolis effect accounts for in the rotating frame of reference.
- The train comes to a stop: From the point of view on the Earth's rotating frame, the velocity of the train is zero, thus the Coriolis force is also zero and the train and its passengers recuperate their usual weight.From the fixed inertial frame of reference above Earth, the train now rotates along with the rest of the Earth. 0.34% of the force of gravity provides the centripetal force needed to achieve the circular motion on that frame of reference. The remaining force, as measured by a scale, makes the train and passengers "lighter" than in the previous case.
- The train travels east. In this case, because it moves in the direction of Earth's rotating frame, the Coriolis term is directed outward from the axis of rotation (up). This upward force makes the train seem lighter still than when at rest.From the fixed inertial frame of reference above Earth, the train traveling east now rotates at twice the rate as when it was at rest—so the amount of centripetal force needed to cause that circular path increases leaving less force from gravity to act on the track. This is what the Coriolis term accounts for on the previous paragraph.As a final check one can imagine a frame of reference rotating along with the train. Such frame would be rotating at twice the angular velocity as Earth's rotating frame. The resulting centrifugal force component for that imaginary frame would be greater. Since the train and its passengers are at rest, that would be the only component in that frame explaining again why the train and the passengers are lighter than in the previous two cases.
This also explains why high-speed projectiles that travel west are deflected down, and those that travel east are deflected up. This vertical component of the Coriolis effect is called the Eötvös effect.[47]
The above example can be used to explain why the Eötvös effect starts diminishing when an object is traveling westward as its tangential speed increases above Earth's rotation (465 m/s). If the westward train in the above example increases speed, part of the force of gravity that pushes against the track accounts for the centripetal force needed to keep it in circular motion on the inertial frame. Once the train doubles its westward speed at 930 m/s (2,100 mph) that centripetal force becomes equal to the force the train experiences when it stops. From the inertial frame, in both cases it rotates at the same speed but in the opposite directions. Thus, the force is the same cancelling completely the Eötvös effect. Any object that moves westward at a speed above 930 m/s (2,100 mph) experiences an upward force instead. In the figure, the Eötvös effect is illustrated for a 10-kilogram (22 lb) object on the train at different speeds. The parabolic shape is because the centripetal force is proportional to the square of the tangential speed. On the inertial frame, the bottom of the parabola is centered at the origin. The offset is because this argument uses the Earth's rotating frame of reference. The graph shows that the Eötvös effect is not symmetrical, and that the resulting downward force experienced by an object that travels west at high velocity is less than the resulting upward force when it travels east at the same speed.
Draining in bathtubs and toilets
Contrary to popular misconception, bathtubs, toilets, and other water receptacles do not drain in opposite directions in the Northern and Southern Hemispheres. This is because the magnitude of the Coriolis force is negligible at this scale.[27][48][49][50] Forces determined by the initial conditions of the water (e.g. the geometry of the drain, the geometry of the receptacle, preexisting momentum of the water, etc.) are likely to be orders of magnitude greater than the Coriolis force and hence will determine the direction of water rotation, if any. For example, identical toilets flushed in both hemispheres drain in the same direction, and this direction is determined mostly by the shape of the toilet bowl.
Under real-world conditions, the Coriolis force does not influence the direction of water flow perceptibly. Only if the water is so still that the effective rotation rate of the Earth is faster than that of the water relative to its container, and if externally applied torques (such as might be caused by flow over an uneven bottom surface) are small enough, the Coriolis effect may indeed determine the direction of the vortex. Without such careful preparation, the Coriolis effect will be much smaller than various other influences on drain direction[51] such as any residual rotation of the water[52] and the geometry of the container.[53]
Laboratory testing of draining water under atypical conditions
In 1962, Ascher Shapiro performed an experiment at MIT to test the Coriolis force on a large basin of water, 2 meters (6 ft 7 in) across, with a small wooden cross above the plug hole to display the direction of rotation, covering it and waiting for at least 24 hours for the water to settle. Under these precise laboratory conditions, he demonstrated the effect and consistent counterclockwise rotation. The experiment required extreme precision, since the acceleration due to Coriolis effect is only [math]\displaystyle{ 3\times 10^{-7} }[/math] that of gravity. The vortex was measured by a cross made of two slivers of wood pinned above the draining hole. It takes 20 minutes to drain, and the cross starts turning only around 15 minutes. At the end it is turning at 1 rotation every 3 to 4 seconds.
He reported that,[54]
Both schools of thought are in some sense correct. For the everyday observations of the kitchen sink and bath-tub variety, the direction of the vortex seems to vary in an unpredictable manner with the date, the time of day, and the particular household of the experimenter. But under well-controlled conditions of experimentation, the observer looking downward at a drain in the northern hemisphere will always see a counter-clockwise vortex, while one in the southern hemisphere will always see a clockwise vortex. In a properly designed experiment, the vortex is produced by Coriolis forces, which are counter-clockwise in the northern hemisphere.
Lloyd Trefethen reported clockwise rotation in the Southern Hemisphere at the University of Sydney in five tests with settling times of 18 h or more.[55]
Ballistic trajectories
The Coriolis force is important in external ballistics for calculating the trajectories of very long-range artillery shells. The most famous historical example was the Paris gun, used by the Germans during World War I to bombard Paris from a range of about 120 km (75 mi). The Coriolis force minutely changes the trajectory of a bullet, affecting accuracy at extremely long distances. It is adjusted for by accurate long-distance shooters, such as snipers. At the latitude of Sacramento, California, a 1,000 yd (910 m) northward shot would be deflected 2.8 in (71 mm) to the right. There is also a vertical component, explained in the Eötvös effect section above, which causes westward shots to hit low, and eastward shots to hit high.[56][57]
The effects of the Coriolis force on ballistic trajectories should not be confused with the curvature of the paths of missiles, satellites, and similar objects when the paths are plotted on two-dimensional (flat) maps, such as the Mercator projection. The projections of the three-dimensional curved surface of the Earth to a two-dimensional surface (the map) necessarily results in distorted features. The apparent curvature of the path is a consequence of the sphericity of the Earth and would occur even in a non-rotating frame.[58]
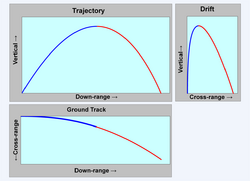
The Coriolis force on a moving projectile depends on velocity components in all three directions, latitude, and azimuth. The directions are typically downrange (the direction that the gun is initially pointing), vertical, and cross-range.[59]:178
- [math]\displaystyle{ A_\mathrm{X} = -2 \omega ( V_\mathrm{Y} \cos \theta_\mathrm{lat} \sin \phi_\mathrm{az} + V_\mathrm{Z} \sin \theta_\mathrm{lat} ) }[/math]
- [math]\displaystyle{ A_\mathrm{Y} = 2 \omega ( V_\mathrm{X} \cos \theta_\mathrm{lat} \sin \phi_\mathrm{az} + V_\mathrm{Z} \cos \theta_\mathrm{lat} \cos \phi_\mathrm{az}) }[/math]
- [math]\displaystyle{ A_\mathrm{Z} = 2 \omega ( V_\mathrm{X} \sin \theta_\mathrm{lat} - V_\mathrm{Y} \cos \theta_\mathrm{lat} \cos \phi_\mathrm{az}) }[/math]
where
- [math]\displaystyle{ A_\mathrm{X} }[/math], down-range acceleration.
- [math]\displaystyle{ A_\mathrm{Y} }[/math], vertical acceleration with positive indicating acceleration upward.
- [math]\displaystyle{ A_\mathrm{Z} }[/math], cross-range acceleration with positive indicating acceleration to the right.
- [math]\displaystyle{ V_\mathrm{X} }[/math], down-range velocity.
- [math]\displaystyle{ V_\mathrm{Y} }[/math], vertical velocity with positive indicating upward.
- [math]\displaystyle{ V_\mathrm{Z} }[/math], cross-range velocity with positive indicating velocity to the right.
- [math]\displaystyle{ \omega }[/math] = 0.00007292 rad/sec, angular velocity of the earth (based on a sidereal day).
- [math]\displaystyle{ \theta_\mathrm{lat} }[/math], latitude with positive indicating Northern hemisphere.
- [math]\displaystyle{ \phi_\mathrm{az} }[/math], azimuth measured clockwise from due North.
Visualization of the Coriolis effect

Red: gravity
Green: the normal force
Blue: the net resultant centripetal force.
To demonstrate the Coriolis effect, a parabolic turntable can be used. On a flat turntable, the inertia of a co-rotating object forces it off the edge. However, if the turntable surface has the correct paraboloid (parabolic bowl) shape (see the figure) and rotates at the corresponding rate, the force components shown in the figure make the component of gravity tangential to the bowl surface exactly equal to the centripetal force necessary to keep the object rotating at its velocity and radius of curvature (assuming no friction). (See banked turn.) This carefully contoured surface allows the Coriolis force to be displayed in isolation.[60][61]
Discs cut from cylinders of dry ice can be used as pucks, moving around almost frictionlessly over the surface of the parabolic turntable, allowing effects of Coriolis on dynamic phenomena to show themselves. To get a view of the motions as seen from the reference frame rotating with the turntable, a video camera is attached to the turntable so as to co-rotate with the turntable, with results as shown in the figure. In the left panel of the figure, which is the viewpoint of a stationary observer, the gravitational force in the inertial frame pulling the object toward the center (bottom ) of the dish is proportional to the distance of the object from the center. A centripetal force of this form causes the elliptical motion. In the right panel, which shows the viewpoint of the rotating frame, the inward gravitational force in the rotating frame (the same force as in the inertial frame) is balanced by the outward centrifugal force (present only in the rotating frame). With these two forces balanced, in the rotating frame the only unbalanced force is Coriolis (also present only in the rotating frame), and the motion is an inertial circle. Analysis and observation of circular motion in the rotating frame is a simplification compared with analysis and observation of elliptical motion in the inertial frame.
Because this reference frame rotates several times a minute rather than only once a day like the Earth, the Coriolis acceleration produced is many times larger and so easier to observe on small time and spatial scales than is the Coriolis acceleration caused by the rotation of the Earth.
In a manner of speaking, the Earth is analogous to such a turntable.[62] The rotation has caused the planet to settle on a spheroid shape, such that the normal force, the gravitational force and the centrifugal force exactly balance each other on a "horizontal" surface. (See equatorial bulge.)
The Coriolis effect caused by the rotation of the Earth can be seen indirectly through the motion of a Foucault pendulum.
Coriolis effects in other areas
Coriolis flow meter
A practical application of the Coriolis effect is the mass flow meter, an instrument that measures the mass flow rate and density of a fluid flowing through a tube. The operating principle involves inducing a vibration of the tube through which the fluid passes. The vibration, though not completely circular, provides the rotating reference frame that gives rise to the Coriolis effect. While specific methods vary according to the design of the flow meter, sensors monitor and analyze changes in frequency, phase shift, and amplitude of the vibrating flow tubes. The changes observed represent the mass flow rate and density of the fluid.[63]
Molecular physics
In polyatomic molecules, the molecule motion can be described by a rigid body rotation and internal vibration of atoms about their equilibrium position. As a result of the vibrations of the atoms, the atoms are in motion relative to the rotating coordinate system of the molecule. Coriolis effects are therefore present, and make the atoms move in a direction perpendicular to the original oscillations. This leads to a mixing in molecular spectra between the rotational and vibrational levels, from which Coriolis coupling constants can be determined.[64]
Gyroscopic precession
When an external torque is applied to a spinning gyroscope along an axis that is at right angles to the spin axis, the rim velocity that is associated with the spin becomes radially directed in relation to the external torque axis. This causes a torque-induced force to act on the rim in such a way as to tilt the gyroscope at right angles to the direction that the external torque would have tilted it. This tendency has the effect of keeping spinning bodies in their rotational frame.
Insect flight
Flies (Diptera) and some moths (Lepidoptera) exploit the Coriolis effect in flight with specialized appendages and organs that relay information about the angular velocity of their bodies. Coriolis forces resulting from linear motion of these appendages are detected within the rotating frame of reference of the insects' bodies. In the case of flies, their specialized appendages are dumbbell shaped organs located just behind their wings called "halteres".[65]
The fly's halteres oscillate in a plane at the same beat frequency as the main wings so that any body rotation results in lateral deviation of the halteres from their plane of motion.[66]
In moths, their antennae are known to be responsible for the sensing of Coriolis forces in the similar manner as with the halteres in flies.[67] In both flies and moths, a collection of mechanosensors at the base of the appendage are sensitive to deviations at the beat frequency, correlating to rotation in the pitch and roll planes, and at twice the beat frequency, correlating to rotation in the yaw plane.[68][67]
Lagrangian point stability
In astronomy, Lagrangian points are five positions in the orbital plane of two large orbiting bodies where a small object affected only by gravity can maintain a stable position relative to the two large bodies. The first three Lagrangian points (L1, L2, L3) lie along the line connecting the two large bodies, while the last two points (L4 and L5) each form an equilateral triangle with the two large bodies. The L4 and L5 points, although they correspond to maxima of the effective potential in the coordinate frame that rotates with the two large bodies, are stable due to the Coriolis effect.[69] The stability can result in orbits around just L4 or L5, known as tadpole orbits, where trojans can be found. It can also result in orbits that encircle L3, L4, and L5, known as horseshoe orbits.
See also
- Analytical mechanics
- Applied mechanics
- Classical mechanics
- Dynamics (mechanics)
- Earth's rotation
- Equatorial Rossby wave
- Frenet–Serret formulas
- Gyroscope
- Kinetics (physics)
- Mechanics of planar particle motion
- Reactive centrifugal force
- Secondary flow
- Statics
- Uniform circular motion
- Whirlpool
References
- ↑ Frautschi, Steven C.; Olenick, Richard P.; Apostol, Tom M.; Goodstein, David L. (2007). The Mechanical Universe: Mechanics and Heat, Advanced Edition (illustrated ed.). Cambridge University Press. p. 396. ISBN 978-0-521-71590-4. https://books.google.com/books?id=ZTnxQGJ1fHMC. Extract of page 396
- ↑ Graney, Christopher M. (2011). "Coriolis effect, two centuries before Coriolis". Physics Today 64 (8): 8. doi:10.1063/PT.3.1195. Bibcode: 2011PhT....64h...8G.
- ↑ Graney, Christopher (24 November 2016). "The Coriolis Effect Further Described in the Seventeenth Century". Physics Today 70 (7): 12–13. doi:10.1063/PT.3.3610. Bibcode: 2017PhT....70g..12G.
- ↑ Truesdell, Clifford. Essays in the History of Mechanics. Springer Science & Business Media, 2012., p. 225
- ↑ Persson, A. "The Coriolis Effect: Four centuries of conflict between common sense and mathematics, Part I: A history to 1885." History of Meteorology 2 (2005): 1–24.
- ↑ Cartwright, David Edgar (2000). Tides: A Scientific History. Cambridge University Press. p. 74. ISBN 9780521797467. https://books.google.com/books?id=78bE5U7TVuIC&pg=PA74.
- ↑ G-G Coriolis (1835). "Sur les équations du mouvement relatif des systèmes de corps" (in French). Journal de l'École Royale Polytechnique 15: 142–154. https://babel.hathitrust.org/cgi/pt?id=mdp.39015005667509&view=1up&seq=152.
- ↑ 8.0 8.1 Persson, Anders (1998-07-01). "How Do We Understand the Coriolis Force?". Bulletin of the American Meteorological Society 79 (7): 1373–1386. doi:10.1175/1520-0477(1998)079<1373:HDWUTC>2.0.CO;2. ISSN 0003-0007. Bibcode: 1998BAMS...79.1373P.
- ↑ Dugas, René and J. R. Maddox (1988). A History of Mechanics. Courier Dover Publications: p. 374. ISBN:0-486-65632-2
- ↑ Price, Bartholomew (1862). A Treatise on Infinitesimal Calculus : Vol. IV. The dynamics of material systems. Oxford : University Press. pp. 418–420. https://books.google.com/books?id=qrMA0R_0TPEC&pg=PA420.
- ↑ Webster, Arthur Gordon (1912). The Dynamics of Particles and of Rigid, Elastic, and Fluid Bodies. B. G. Teubner. p. 320. ISBN 978-1-113-14861-2. https://archive.org/details/dynamicsparticl04websgoog.
- ↑ Wilson, Edwin B. (1920). Cattell, James McKeen. ed. "Space, Time, and Gravitation". The Scientific Monthly 10: 226. https://books.google.com/books?id=xYUZAAAAYAAJ&pg=PA226.
- ↑ Ferrel, William (November 1856). "An Essay on the Winds and the Currents of the Ocean". Nashville Journal of Medicine and Surgery xi (4): 7–19. http://www.aos.princeton.edu/WWWPUBLIC/gkv/history/ferrel-nashville56.pdf. Retrieved on 1 January 2009.
- ↑ Persson, Anders O.. The Coriolis Effect:Four centuries of conflict between common sense and mathematics, Part I: A history to 1885. Swedish Meteorological and Hydrological Institute. http://www.meteohistory.org/2005historyofmeteorology2/01persson.pdf. Retrieved 26 February 2006.
- ↑ Gerkema, Theo; Gostiaux, Louis (2012). "A brief history of the Coriolis force". Europhysics News 43 (2): 16. doi:10.1051/epn/2012202. Bibcode: 2012ENews..43b..14G.
- ↑ Bhatia, V.B. (1997). Classical Mechanics: With introduction to Nonlinear Oscillations and Chaos. Narosa Publishing House. p. 201. ISBN 978-81-7319-105-3.
- ↑ Silverman, Mark P. (2002). A Universe of Atoms, an Atom in the Universe (2nd ed.). Berlin, Germany: Springer. p. 249. ISBN 9780387954370. https://books.google.com/books?id=-Er5pIsYe_AC&pg=PA249.
- ↑ Taylor (2005). p. 329.
- ↑ Lee, Choonkyu; Min, Hyunsoo (17 April 2018) (in en). Essential Classical Mechanics. World Scientific Publishing Company. ISBN 978-981-323-466-6. https://books.google.com/books?id=_WdhDwAAQBAJ&q=coriolis+frame+of+reference&pg=PT506. Retrieved 13 March 2021.
- ↑ Lanczos, Cornelius (1986). The Variational Principles of Mechanics (4th (reprint) ed.). Mineola, NY: Dover Publications. p. Chapter 4, §5. ISBN 9780486650678. https://books.google.com/books?id=ZWoYYr8wk2IC&pg=PA103.
- ↑ Tavel, Morton (2002). Contemporary Physics and the Limits of Knowledge. New Brunswick, NJ: Rutgers University Press. p. 93. ISBN 9780813530772. https://books.google.com/books?id=SELS0HbIhjYC&q=Einstein+equivalence+laws+physics+frame&pg=PA95. "Finally, noninertial forces, like centrifugal and Coriolis forces, can be eliminated by jumping into a reference frame that moves with constant velocity, the frame that Newton called inertial."
- ↑ Graney, Christopher M. (2015). Setting Aside All Authority: Giovanni Battista Riccioli and the Science Against Copernicus in the Age of Galileo. Notre Dame, IN: University of Notre Dame Press. pp. 115–125. ISBN 9780268029883. https://books.google.com/books?id=6r_nrQEACAAJ.
- ↑ Beckers, Benoit (2013). Solar Energy at Urban Scale. John Wiley & Sons. p. 116. ISBN 978-1-118-61436-5. https://books.google.com/books?id=GAOnjP4k7SQC. Extract of page 116
- ↑ Toossi, Reza (2009). Energy and the Environment: Resources, Technologies, and Impacts. Verve Publishers. p. 48. ISBN 978-1-4276-1867-2. https://books.google.com/books?id=-cb2EyrWbg0C. Extract of page 48
- ↑ "MIT: Flow in rotating environments". https://ocw.mit.edu/courses/earth-atmospheric-and-planetary-sciences/12-090-introduction-to-fluid-motions-sediment-transport-and-current-generated-sedimentary-structures-fall-2006/course-textbook/ch7.pdf.
- ↑ Shakur, Asif (2014). "Debunking Coriolis Force Myths". The Physics Teacher 52 (8): 464–465. doi:10.1119/1.4897580. Bibcode: 2014PhTea..52..464S.
- ↑ 27.0 27.1 Scientific American Staff, and Hanson, Brad; Decker, Fred W.; Ehrlich, Robert & Humphrey, Thomas (January 28, 2001). "Can Somebody Finally Settle This Question: Does Water Flowing Down a Drain Spin in Different Directions Depending on Which Hemisphere You're In? And If So, Why?" (serial expert interviews). ScientificAmerican.com. Berlin: Scientific American-Springer Nature. https://www.scientificamerican.com/article/can-somebody-finally-sett/.
- ↑ "Coriolis Force Effect on Drains". 28 April 2003. https://www.snopes.com/fact-check/coriolis-effect/.
- ↑ Kantha, Lakshmi H. & Clayson, Carol Anne (2000). Numerical Models of Oceans and Oceanic Processes. New York, NY: Academic Press. p. 103. ISBN 9780124340688. https://books.google.com/books?id=Gps9JXtd3owC&pg=PA103.
- ↑ Butz, Stephen D. (2002). Science of Earth Systems. Stamford, CT: Thomson Delmar Learning. p. 305. ISBN 9780766833913. https://books.google.com/books?id=JB4ArbvXXDEC&pg=PA304.
- ↑ Holton, James R. (2004). An Introduction to Dynamic Meteorology. New York, NY: Academic Press. p. 18. ISBN 9780123540157. https://books.google.com/books?id=fhW5oDv3EPsC&pg=PA18.
- ↑ Carlucci, Donald E.; Jacobson, Sidney S. (2007). Ballistics: Theory and Design of Guns and Ammunition. CRC Press. pp. 224–226. ISBN 978-1-4200-6618-0. https://books.google.com/books?id=pX9Tzs7VuSoC&pg=PA224.
- ↑ Menke, WIlliam & Abbott, Dallas (1990). Geophysical Theory. New York, NY: Columbia University Press. pp. 124–126. ISBN 9780231067928. https://books.google.com/books?id=XP3R_pVnOoEC&pg=PA120.
- ↑ Holton, James R. (2004). An Introduction to Dynamic Meteorology. Burlington, MA: Elsevier Academic Press. p. 64. ISBN 9780123540157. https://books.google.com/books?id=fhW5oDv3EPsC&pg=PA64.
- ↑ Brinney, Amanda. "What Is the Coriolis Effect?". ThoughtCo.com. https://www.thoughtco.com/what-is-the-coriolis-effect-1435315.
- ↑ Evers, Jeannie (Ed.) (May 2, 2023). "The Coriolis Effect: Earth's Rotation and Its Effect on Weather" (in en) (grades 3-12 teaching resource). Washington, DC: National Geographic Society. https://www.nationalgeographic.org/encyclopedia/coriolis-effect/.
- ↑ Barry, Roger Graham & Chorley, Richard J. (2003). Atmosphere, Weather and Climate. Abingdon-on-Thames, Oxfordshire, England: Routledge-Taylor & Francis. p. 115. ISBN 9780415271714. https://books.google.com/books?id=MUQOAAAAQAAJ&pg=PA115.
- ↑ Nelson, Stephen (Fall 2014). "Tropical Cyclones (Hurricanes)". Wind Systems: Low Pressure Centers. New Orleans, LA: Tulane University. http://www.tulane.edu/~sanelson/New_Orleans_and_Hurricanes/tropical_cyclones.htm.
- ↑ For instance, see the image appearing in this source: NASA Staff. "Cloud Spirals and Outflow in Tropical Storm Katrina from Earth Observatory". JPL.NASA.gov. NASA. https://photojournal.jpl.nasa.gov/catalog/PIA04384.[full citation needed]
- ↑ Penuel, K. Bradley; Statler, Matt (2010-12-29) (in en). Encyclopedia of Disaster Relief. SAGE Publications. p. 326. ISBN 9781452266398. https://books.google.com/books?id=XRxzAwAAQBAJ&pg=PA326.
- ↑ Marshall, John; Plumb, R. Alan (2007). Atmosphere, Ocean and Climate Dynamics: An Introductory Text. Amsterdam: Elsevier Academic Press. p. 98. ISBN 9780125586917. https://books.google.com/books?id=aTGYbmVaA_gC&pg=PA98.
- ↑ Lowrie, William (1997). Fundamentals of Geophysics (illustrated ed.). Cambridge University Press. p. 45. ISBN 978-0-521-46728-5. https://books.google.com/books?id=7vR2RJSIGVoC. Extract of page 45
- ↑ Ong, H.; Roundy, P.E. (2020). "Nontraditional hypsometric equation". Q. J. R. Meteorol. Soc. 146 (727): 700–706. doi:10.1002/qj.3703. Bibcode: 2020QJRMS.146..700O.
- ↑ Hayashi, M.; Itoh, H. (2012). "The Importance of the Nontraditional Coriolis Terms in Large-Scale Motions in the Tropics Forced by Prescribed Cumulus Heating". J. Atmos. Sci. 69 (9): 2699–2716. doi:10.1175/JAS-D-11-0334.1. Bibcode: 2012JAtS...69.2699H.
- ↑ Ong, H.; Roundy, P.E. (2019). "Linear effects of nontraditional Coriolis terms on intertropical convergence zone forced large-scale flow". Q. J. R. Meteorol. Soc. 145 (723): 2445–2453. doi:10.1002/qj.3572. Bibcode: 2019QJRMS.145.2445O.
- ↑ 46.0 46.1 Persson, Anders. The Coriolis Effect – a conflict between common sense and mathematics. Norrköping, Sweden: The Swedish Meteorological and Hydrological Institute. p. 8. http://met.no/english/topics/nomek_2005/coriolis.pdf. Retrieved 6 September 2015.
- ↑ Lowrie, William (2011) (in en). A Student's Guide to Geophysical Equations. Cambridge University Press. p. 141. ISBN 978-1-139-49924-8. https://books.google.com/books?id=HPE1C9vtWZ0C&pg=PA141. Retrieved 25 February 2020.
- ↑ Fraser, Alistair B.. "Bad Coriolis... Bad Meteorology" (teacher's resource). EMS.PSU.edu. http://www.ems.psu.edu/~fraser/Bad/BadCoriolis.html.
- ↑ "Flush Bosh". www.snopes.com. 28 April 2003. http://www.snopes.com/science/coriolis.asp.
- ↑ "Does the rotation of the Earth affect toilets and baseball games?". 2009-07-20. http://science.howstuffworks.com/science-vs-myth/everyday-myths/rotation-earth-toilet-baseball2.htm.
- ↑ Kirkpatrick, Larry D.; Francis, Gregory E. (2006). Physics: A World View. Cengage Learning. pp. 168–9. ISBN 978-0-495-01088-3. https://books.google.com/books?id=8hOLs-bmiYYC&pg=PA168.
- ↑ Y. A. Stepanyants; G. H. Yeoh (2008). "Stationary bathtub vortices and a critical regime of liquid discharge". Journal of Fluid Mechanics 604 (1): 77–98. doi:10.1017/S0022112008001080. Bibcode: 2008JFM...604...77S. http://eprints.usq.edu.au/5726/2/Stepanyants_Yeoh_2008_PV.pdf.
- ↑ Creative Media Applications (2004). A Student's Guide to Earth Science: Words and terms. Greenwood Publishing Group. p. 22. ISBN 978-0-313-32902-9. https://books.google.com/books?id=fF0TTZVQuZoC&pg=PA22.
- ↑ Shapiro, Ascher H. (December 1962). "Bath-Tub Vortex". Nature 196 (4859): 1080–1081. doi:10.1038/1961080b0. Bibcode: 1962Natur.196.1080S.
- ↑ Trefethen, Lloyd M.; Bilger, R. W.; Fink, P. T.; Luxton, R. E.; Tanner, R. I. (September 1965). "The Bath-Tub Vortex in the Southern Hemisphere". Nature 207 (5001): 1084–1085. doi:10.1038/2071084a0. Bibcode: 1965Natur.207.1084T.
- ↑ The claim is made that in the Falklands in WW I, the British failed to correct their sights for the southern hemisphere, and so missed their targets. John Edensor Littlewood (1953). A Mathematician's Miscellany. Methuen And Company Limited. p. 51. https://archive.org/details/mathematiciansmi033496mbp. John Robert Taylor (2005). Classical Mechanics. University Science Books. p. 364; Problem 9.28. ISBN 978-1-891389-22-1. https://books.google.com/books?id=P1kCtNr-pJsC&pg=PA364. For set up of the calculations, see Carlucci & Jacobson (2007), p. 225
- ↑ "Do Snipers Compensate for the Earth's Rotation?" (in en). Washington City Paper. 25 June 2010. https://www.washingtoncitypaper.com/columns/straight-dope/article/13039128/do-snipers-compensate-for-the-earthrsquos-rotation-what-the-coriolis.
- ↑ Klinger, Barry A.; Haine, Thomas W. N. (2019). "Deep Meridional Overturning". Ocean Circulation in Three Dimensions. Cambridge University Press. ISBN 978-0521768436. https://books.google.com/books?id=Kr2GDwAAQBAJ&pg=PA291. Retrieved 2019-08-19.
- ↑ McCoy, Robert L. (1999), Modern Exterior Ballistics, Schiffer Military History, ISBN 0-7643-0720-7
- ↑ When a container of fluid is rotating on a turntable, the surface of the fluid naturally assumes the correct parabolic shape. This fact may be exploited to make a parabolic turntable by using a fluid that sets after several hours, such as a synthetic resin. For a video of the Coriolis effect on such a parabolic surface, see Geophysical fluid dynamics lab demonstration John Marshall, Massachusetts Institute of Technology.
- ↑ For a java applet of the Coriolis effect on such a parabolic surface, see Brian Fiedler School of Meteorology at the University of Oklahoma.
- ↑ John Marshall; R. Alan Plumb (2007). Atmosphere, Ocean, and Climate Dynamics: An Introductory Text. Academic Press. p. 101. ISBN 978-0-12-558691-7. https://books.google.com/books?id=aTGYbmVaA_gC&pg=PA101.
- ↑ Omega Engineering. Mass Flowmeters. http://www.omega.com/literature/transactions/volume4/t9904-10-mass.html.
- ↑ califano, S (1976). Vibrational states. Wiley. pp. 226–227. ISBN 978-0471129967.
- ↑ Fraenkel, G.; Pringle, W.S. (21 May 1938). "Halteres of Flies as Gyroscopic Organs of Equilibrium". Nature 141 (3577): 919–920. doi:10.1038/141919a0. Bibcode: 1938Natur.141..919F.
- ↑ Dickinson, M. (1999). "Haltere-mediated equilibrium reflexes of the fruit fly, Drosophila melanogaster". Phil. Trans. R. Soc. Lond. 354 (1385): 903–916. doi:10.1098/rstb.1999.0442. PMID 10382224.
- ↑ 67.0 67.1 Sane S., Dieudonné, A., Willis, M., Daniel, T. (February 2007). "Antennal mechanosensors mediate flight control in moths". Science 315 (5813): 863–866. doi:10.1126/science.1133598. PMID 17290001. Bibcode: 2007Sci...315..863S. http://www.hep.princeton.edu/%7Emcdonald/examples/mechanics/sane_science_315_863_07.pdf. Retrieved 1 December 2017.
- ↑ Fox, J; Daniel, T (2008). "A neural basis for gyroscopic force measurement in the halteres of Holorusia". Journal of Comparative Physiology 194 (10): 887–897. doi:10.1007/s00359-008-0361-z. PMID 18751714.
- ↑ Spohn, Tilman; Breuer, Doris; Johnson, Torrence (2014). Encyclopedia of the Solar System. Elsevier. p. 60. ISBN 978-0124160347. https://books.google.com/books?id=0bEMAwAAQBAJ&pg=PP1.
Further reading
Physics and meteorology
- Riccioli, G. B., 1651: Almagestum Novum, Bologna, pp. 425–427
(Original book [in Latin], scanned images of complete pages.) - Coriolis, G. G., 1832: "Mémoire sur le principe des forces vives dans les mouvements relatifs des machines." Journal de l'école Polytechnique, Vol 13, pp. 268–302.
(Original article [in French], PDF file, 1.6 MB, scanned images of complete pages.) - Coriolis, G. G., 1835: "Mémoire sur les équations du mouvement relatif des systèmes de corps." Journal de l'école Polytechnique, Vol 15, pp. 142–154
(Original article [in French] PDF file, 400 KB, scanned images of complete pages.) - Gill, A. E. Atmosphere-Ocean dynamics, Academic Press, 1982.
- Robert Ehrlich (1990). Turning the World Inside Out and 174 Other Simple Physics Demonstrations. Princeton University Press. p. Rolling a ball on a rotating turntable; p. 80 ff. ISBN 978-0-691-02395-3. https://archive.org/details/turningworldinsi00ehrl/page/.
- Durran, D. R., 1993: Is the Coriolis force really responsible for the inertial oscillation?, Bull. Amer. Meteor. Soc., 74, pp. 2179–2184; Corrigenda. Bulletin of the American Meteorological Society, 75, p. 261
- Durran, D. R., and S. K. Domonkos, 1996: An apparatus for demonstrating the inertial oscillation, Bulletin of the American Meteorological Society, 77, pp. 557–559.
- Marion, Jerry B. 1970, Classical Dynamics of Particles and Systems, Academic Press.
- Persson, A., 1998 [1] How do we Understand the Coriolis Force? Bulletin of the American Meteorological Society 79, pp. 1373–1385.
- Symon, Keith. 1971, Mechanics, Addison–Wesley
- Akira Kageyama & Mamoru Hyodo: Eulerian derivation of the Coriolis force
- James F. Price: A Coriolis tutorial Woods Hole Oceanographic Institute (2003)
- McDonald, James E. (May 1952). "The Coriolis Effect". Scientific American 186 (5): 72–78. doi:10.1038/scientificamerican0552-72. Bibcode: 1952SciAm.186e..72M. http://physics.oregonstate.edu/~kustuscm/COURSES/ph429/2013/handouts/McDonald1952.pdf. Retrieved 2016-01-04. "Everything that moves over the surface of the Earth – water, air, animals, machines and projectiles – sidles to the right in the Northern Hemisphere and to the left in the Southern".. Elementary, non-mathematical; but well written.
Historical
- Grattan-Guinness, I., Ed., 1994: Companion Encyclopedia of the History and Philosophy of the Mathematical Sciences. Vols. I and II. Routledge, 1840 pp.
1997: The Fontana History of the Mathematical Sciences. Fontana, 817 pp. 710 pp. - Khrgian, A., 1970: Meteorology: A Historical Survey. Vol. 1. Keter Press, 387 pp.
- Kuhn, T. S., 1977: Energy conservation as an example of simultaneous discovery. The Essential Tension, Selected Studies in Scientific Tradition and Change, University of Chicago Press, 66–104.
- Kutzbach, G., 1979: The Thermal Theory of Cyclones. A History of Meteorological Thought in the Nineteenth Century. Amer. Meteor. Soc., 254 pp.
External links
| Wikimedia Commons has media related to Coriolis effect. |
- The definition of the Coriolis effect from the Glossary of Meteorology
- The Coriolis Effect — a conflict between common sense and mathematics PDF-file. 20 pages. A general discussion by Anders Persson of various aspects of the coriolis effect, including Foucault's Pendulum and Taylor columns.
- The coriolis effect in meteorology PDF-file. 5 pages. A detailed explanation by Mats Rosengren of how the gravitational force and the rotation of the Earth affect the atmospheric motion over the Earth surface. 2 figures
- 10 Coriolis Effect Videos and Games- from the About.com Weather Page
- Coriolis Force – from ScienceWorld
- Coriolis Effect and Drains An article from the NEWTON web site hosted by the Argonne National Laboratory.
- Catalog of Coriolis videos
- Coriolis Effect: A graphical animation, a visual Earth animation with precise explanation
- An introduction to fluid dynamics SPINLab Educational Film explains the Coriolis effect with the aid of lab experiments
- Do bathtubs drain counterclockwise in the Northern Hemisphere? by Cecil Adams.
- Bad Coriolis. An article uncovering misinformation about the Coriolis effect. By Alistair B. Fraser, emeritus professor of meteorology at Pennsylvania State University
- The Coriolis Effect: A (Fairly) Simple Explanation, an explanation for the layperson
- Observe an animation of the Coriolis effect over Earth's surface
- Animation clip showing scenes as viewed from both an inertial frame and a rotating frame of reference, visualizing the Coriolis and centrifugal forces.
- Vincent Mallette The Coriolis Force @ INWIT
- NASA notes
- Interactive Coriolis Fountain lets you control rotation speed, droplet speed and frame of reference to explore the Coriolis effect.
- Rotating Co-ordinating Systems , transformation from inertial systems
 |