Physics:Hartree–Fock method
In computational physics and chemistry, the Hartree–Fock (HF) method is a method of approximation for the determination of the wave function and the energy of a quantum many-body system in a stationary state.
The Hartree–Fock method often assumes that the exact N-body wave function of the system can be approximated by a single Slater determinant (in the case where the particles are fermions) or by a single permanent (in the case of bosons) of N spin-orbitals. By invoking the variational method, one can derive a set of N-coupled equations for the N spin orbitals. A solution of these equations yields the Hartree–Fock wave function and energy of the system. Hartree–Fock approximation is an instance of mean-field theory,[1] where neglecting higher-order fluctuations in order parameter allows replacing interaction terms with quadratic terms, obtaining exactly solvable Hamiltonians.
Especially in the older literature, the Hartree–Fock method is also called the self-consistent field method (SCF). In deriving what is now called the Hartree equation as an approximate solution of the Schrödinger equation, Hartree required the final field as computed from the charge distribution to be "self-consistent" with the assumed initial field. Thus, self-consistency was a requirement of the solution. The solutions to the non-linear Hartree–Fock equations also behave as if each particle is subjected to the mean field created by all other particles (see the Fock operator below), and hence the terminology continued. The equations are almost universally solved by means of an iterative method, although the fixed-point iteration algorithm does not always converge.[2] This solution scheme is not the only one possible and is not an essential feature of the Hartree–Fock method.
The Hartree–Fock method finds its typical application in the solution of the Schrödinger equation for atoms, molecules, nanostructures[3] and solids but it has also found widespread use in nuclear physics. (See Hartree–Fock–Bogoliubov method for a discussion of its application in nuclear structure theory). In atomic structure theory, calculations may be for a spectrum with many excited energy levels, and consequently, the Hartree–Fock method for atoms assumes the wave function is a single configuration state function with well-defined quantum numbers and that the energy level is not necessarily the ground state.
For both atoms and molecules, the Hartree–Fock solution is the central starting point for most methods that describe the many-electron system more accurately.
The rest of this article will focus on applications in electronic structure theory suitable for molecules with the atom as a special case. The discussion here is only for the restricted Hartree–Fock method, where the atom or molecule is a closed-shell system with all orbitals (atomic or molecular) doubly occupied. Open-shell systems, where some of the electrons are not paired, can be dealt with by either the restricted open-shell or the unrestricted Hartree–Fock methods.
Brief history
Early semi-empirical methods
The origin of the Hartree–Fock method dates back to the end of the 1920s, soon after the discovery of the Schrödinger equation in 1926. Douglas Hartree's methods were guided by some earlier, semi-empirical methods of the early 1920s (by E. Fues, R. B. Lindsay, and himself) set in the old quantum theory of Bohr.
In the Bohr model of the atom, the energy of a state with principal quantum number n is given in atomic units as [math]\displaystyle{ E = -1 / n^2 }[/math]. It was observed from atomic spectra that the energy levels of many-electron atoms are well described by applying a modified version of Bohr's formula. By introducing the quantum defect d as an empirical parameter, the energy levels of a generic atom were well approximated by the formula [math]\displaystyle{ E = -1 / (n + d)^2 }[/math], in the sense that one could reproduce fairly well the observed transitions levels observed in the X-ray region (for example, see the empirical discussion and derivation in Moseley's law). The existence of a non-zero quantum defect was attributed to electron–electron repulsion, which clearly does not exist in the isolated hydrogen atom. This repulsion resulted in partial screening of the bare nuclear charge. These early researchers later introduced other potentials containing additional empirical parameters with the hope of better reproducing the experimental data.
Hartree method
In 1927, D. R. Hartree introduced a procedure, which he called the self-consistent field method, to calculate approximate wave functions and energies for atoms and ions.[4] Hartree sought to do away with empirical parameters and solve the many-body time-independent Schrödinger equation from fundamental physical principles, i.e., ab initio. His first proposed method of solution became known as the Hartree method, or Hartree product. However, many of Hartree's contemporaries did not understand the physical reasoning behind the Hartree method: it appeared to many people to contain empirical elements, and its connection to the solution of the many-body Schrödinger equation was unclear. However, in 1928 J. C. Slater and J. A. Gaunt independently showed that the Hartree method could be couched on a sounder theoretical basis by applying the variational principle to an ansatz (trial wave function) as a product of single-particle functions.[5][6]
In 1930, Slater and V. A. Fock independently pointed out that the Hartree method did not respect the principle of antisymmetry of the wave function.[7] [8] The Hartree method used the Pauli exclusion principle in its older formulation, forbidding the presence of two electrons in the same quantum state. However, this was shown to be fundamentally incomplete in its neglect of quantum statistics.
Hartree–Fock
A solution to the lack of anti-symmetry in the Hartree method came when it was shown that a Slater determinant, a determinant of one-particle orbitals first used by Heisenberg and Dirac in 1926, trivially satisfies the antisymmetric property of the exact solution and hence is a suitable ansatz for applying the variational principle. The original Hartree method can then be viewed as an approximation to the Hartree–Fock method by neglecting exchange. Fock's original method relied heavily on group theory and was too abstract for contemporary physicists to understand and implement. In 1935, Hartree reformulated the method to be more suitable for the purposes of calculation.[9]
The Hartree–Fock method, despite its physically more accurate picture, was little used until the advent of electronic computers in the 1950s due to the much greater computational demands over the early Hartree method and empirical models.[10] Initially, both the Hartree method and the Hartree–Fock method were applied exclusively to atoms, where the spherical symmetry of the system allowed one to greatly simplify the problem. These approximate methods were (and are) often used together with the central field approximation to impose the condition that electrons in the same shell have the same radial part and to restrict the variational solution to be a spin eigenfunction. Even so, calculating a solution by hand using the Hartree–Fock equations for a medium-sized atom was laborious; small molecules required computational resources far beyond what was available before 1950.
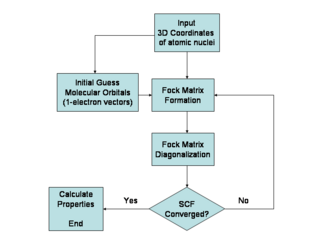
Hartree–Fock algorithm
The Hartree–Fock method is typically used to solve the time-independent Schrödinger equation for a multi-electron atom or molecule as described in the Born–Oppenheimer approximation. Since there are no known analytic solutions for many-electron systems (there are solutions for one-electron systems such as hydrogenic atoms and the diatomic hydrogen cation), the problem is solved numerically. Due to the nonlinearities introduced by the Hartree–Fock approximation, the equations are solved using a nonlinear method such as iteration, which gives rise to the name "self-consistent field method."
Approximations
The Hartree–Fock method makes five major simplifications to deal with this task:
- The Born–Oppenheimer approximation is inherently assumed. The full molecular wave function is actually a function of the coordinates of each of the nuclei, in addition to those of the electrons.
- Typically, relativistic effects are completely neglected. The momentum operator is assumed to be completely non-relativistic.
- The variational solution is assumed to be a linear combination of a finite number of basis functions, which are usually (but not always) chosen to be orthogonal. The finite basis set is assumed to be approximately complete.
- Each energy eigenfunction is assumed to be describable by a single Slater determinant, an antisymmetrized product of one-electron wave functions (i.e., orbitals).
- The mean-field approximation is implied. Effects arising from deviations from this assumption are neglected. These effects are often collectively used as a definition of the term electron correlation. However, the label "electron correlation" strictly spoken encompasses both the Coulomb correlation and Fermi correlation, and the latter is an effect of electron exchange, which is fully accounted for in the Hartree–Fock method.[11][12] Stated in this terminology, the method only neglects the Coulomb correlation. However, this is an important flaw, accounting for (among others) Hartree–Fock's inability to capture London dispersion.[13]
Relaxation of the last two approximations give rise to many so-called post-Hartree–Fock methods.
Variational optimization of orbitals
The variational theorem states that for a time-independent Hamiltonian operator, any trial wave function will have an energy expectation value that is greater than or equal to the true ground-state wave function corresponding to the given Hamiltonian. Because of this, the Hartree–Fock energy is an upper bound to the true ground-state energy of a given molecule. In the context of the Hartree–Fock method, the best possible solution is at the Hartree–Fock limit; i.e., the limit of the Hartree–Fock energy as the basis set approaches completeness. (The other is the full-CI limit, where the last two approximations of the Hartree–Fock theory as described above are completely undone. It is only when both limits are attained that the exact solution, up to the Born–Oppenheimer approximation, is obtained.) The Hartree–Fock energy is the minimal energy for a single Slater determinant.
The starting point for the Hartree–Fock method is a set of approximate one-electron wave functions known as spin-orbitals. For an atomic orbital calculation, these are typically the orbitals for a hydrogen-like atom (an atom with only one electron, but the appropriate nuclear charge). For a molecular orbital or crystalline calculation, the initial approximate one-electron wave functions are typically a linear combination of atomic orbitals (LCAO).
The orbitals above only account for the presence of other electrons in an average manner. In the Hartree–Fock method, the effect of other electrons are accounted for in a mean-field theory context. The orbitals are optimized by requiring them to minimize the energy of the respective Slater determinant. The resultant variational conditions on the orbitals lead to a new one-electron operator, the Fock operator. At the minimum, the occupied orbitals are eigensolutions to the Fock operator via a unitary transformation between themselves. The Fock operator is an effective one-electron Hamiltonian operator being the sum of two terms. The first is a sum of kinetic-energy operators for each electron, the internuclear repulsion energy, and a sum of nuclear–electronic Coulombic attraction terms. The second are Coulombic repulsion terms between electrons in a mean-field theory description; a net repulsion energy for each electron in the system, which is calculated by treating all of the other electrons within the molecule as a smooth distribution of negative charge. This is the major simplification inherent in the Hartree–Fock method and is equivalent to the fifth simplification in the above list.
Since the Fock operator depends on the orbitals used to construct the corresponding Fock matrix, the eigenfunctions of the Fock operator are in turn new orbitals, which can be used to construct a new Fock operator. In this way, the Hartree–Fock orbitals are optimized iteratively until the change in total electronic energy falls below a predefined threshold. In this way, a set of self-consistent one-electron orbitals is calculated. The Hartree–Fock electronic wave function is then the Slater determinant constructed from these orbitals. Following the basic postulates of quantum mechanics, the Hartree–Fock wave function can then be used to compute any desired chemical or physical property within the framework of the Hartree–Fock method and the approximations employed.
Mathematical formulation
Derivation
To derive Hartree-Fock we minimize the energy functional for N electrons
- [math]\displaystyle{ \delta E[\phi_k^*(x_k)] = \delta \left\langle\psi^{HF}|H^e|\psi^{HF}\right\rangle - \delta\left[\sum_{i=1}^N \sum_{j=1}^N \lambda_{ij} \left( \left\langle\phi_i, \phi_j\right\rangle - \delta_{ij}\right)\right] \stackrel{!}{=}\, 0, }[/math]
where [math]\displaystyle{ H^e }[/math] is the molecular Hamiltonian in the Born-Oppenheimer approximation, [math]\displaystyle{ \psi^{HF} }[/math] is the one Slater determinant Hartree-Fock wave function and the second term is the sum over a Lagrange multiplier [math]\displaystyle{ \lambda_{ij} }[/math] and the constraint that the spin orbitals [math]\displaystyle{ \phi_i(x_i) }[/math] of the Slater determinant
- [math]\displaystyle{ \begin{aligned} \psi(\mathbf{x}_1, \mathbf{x}_2, \ldots, \mathbf{x}_N) &= \frac{1}{\sqrt{N!}} \begin{vmatrix} \phi_1(\mathbf{x}_1) & \phi_2(\mathbf{x}_1) & \cdots & \phi_N(\mathbf{x}_1) \\ \phi_1(\mathbf{x}_2) & \phi_2(\mathbf{x}_2) & \cdots & \phi_N(\mathbf{x}_2) \\ \vdots & \vdots & \ddots & \vdots \\ \phi_1(\mathbf{x}_N) & \phi_2(\mathbf{x}_N) & \cdots & \phi_N(\mathbf{x}_N) \end{vmatrix}, \end{aligned} }[/math]
are orthonormal. Since we can choose the basis of [math]\displaystyle{ \phi_i(x_i) }[/math], we choose a basis in which the Lagrange multiplier matrix [math]\displaystyle{ \lambda_{ij} }[/math] becomes diagonal, i.e. [math]\displaystyle{ \lambda_{ij} = \epsilon_i \delta_{ij} }[/math]. Performing the variation, we obtain
- [math]\displaystyle{ \begin{aligned} \delta E[\phi_k^*(x_k)] &= \sum_{i=1}^N \int\text{d}\mathbf{x}_i \, h^1(\mathbf{x}_i) \phi_i(\mathbf{x}_i) \delta(\mathbf{x}_i -\mathbf{x}_k) \delta_{ik}\\ &+ \sum_{i=1}^N\sum_{j=1}^N \int \mathrm{d}\mathbf{x}_i \int \text{d}\mathbf{x}_j\phi_j^*(\mathbf{x}_j) \frac{1}{|\mathbf{r}_i-\mathbf{r}_j|}\phi_i(\mathbf{x}_i)\phi_j(\mathbf{x}_j) \delta(\mathbf{x}_i-\mathbf{x}_k)\delta_{ik}\\ &- \sum_{i=1}^N\sum_{j=1}^N \int \text{d}\mathbf{x}_i \int \text{d}\mathbf{x}_j\phi_j^*(\mathbf{x}_j) \frac{1}{|\mathbf{r}_i-\mathbf{r}_j|}\phi_i(\mathbf{x}_j)\phi_j(\mathbf{x}_i) \delta(\mathbf{x}_i-\mathbf{x}_k)\delta_{ik}\\ &+ \sum_{i=1}^N \epsilon_i \int \text{d}\mathbf{x}_i \, \phi_i(\mathbf{x}_i) \delta(\mathbf{x}_i-\mathbf{x}_k)\delta_{ik}\\ \\ &= h^1(\mathbf{x}_k) \phi_k(\mathbf{x}_k)\\ &+ \sum_{j=1}^N \int \text{d}\mathbf{x}_j\phi_j^*(\mathbf{x}_j) \frac{1}{|\mathbf{r}_k-\mathbf{r}_j|}\phi_k(\mathbf{x}_k)\phi_j(\mathbf{x}_j)\\ &- \sum_{j=1}^N \int \text{d}\mathbf{x}_j\phi_j^*(\mathbf{x}_j) \frac{1}{|\mathbf{r}_k-\mathbf{r}_j|}\phi_k(\mathbf{x}_j)\phi_j(\mathbf{x}_k)\\ &+ \epsilon_k \phi_k(\mathbf{x}_k). \\ \end{aligned} }[/math]
The factor 1/2 in the molecular Hamiltonian drops out before the double integrals due to symmetry and the product rule. We find the Fock equation
- [math]\displaystyle{ F(\mathbf{x}_k)\phi_k = \epsilon_k \phi_k = h^1(\mathbf{x}_k) + J(\mathbf{x}_k) - K(\mathbf{x}_k), }[/math]
where the Coulomb operator [math]\displaystyle{ J(\mathbf{x}_k) }[/math] and the exchange operator [math]\displaystyle{ K(\mathbf{x}_k) }[/math] are defined as follows
- [math]\displaystyle{ \begin{aligned} J(\mathbf{x_k}) &= \int \mathrm{d}\mathbf{x}_j \frac{\rho(\mathbf{x}_j)}{|\mathbf{r}_k-\mathbf{r}_j|},\\ K(\mathbf{x_k})\phi_{k}(\mathbf{x}_k) &= \sum_{j=1}^N \phi_{j}(\mathbf{x}_k) \int \text{d}\mathbf{x}_j \frac{\phi_j^*(\mathbf{x}_j) \phi_k(\mathbf{x}_j)}{|\mathbf{r}_k-\mathbf{r}_j|}.\\ \end{aligned} }[/math]
The exchange operator has no classical analogue and can only be defined as an integral operator.
The Fock operator
Because the electron–electron repulsion term of the molecular Hamiltonian involves the coordinates of two different electrons, it is necessary to reformulate it in an approximate way. Under this approximation (outlined under Hartree–Fock algorithm), all of the terms of the exact Hamiltonian except the nuclear–nuclear repulsion term are re-expressed as the sum of one-electron operators outlined below, for closed-shell atoms or molecules (with two electrons in each spatial orbital).[14] The "(1)" following each operator symbol simply indicates that the operator is 1-electron in nature.
- [math]\displaystyle{ \hat F[\{\phi_j\}](1) = \hat H^\text{core}(1) + \sum_{j=1}^{N/2} [2\hat J_j(1) - \hat K_j(1)], }[/math]
where
- [math]\displaystyle{ \hat F[\{\phi_j\}](1) }[/math]
is the one-electron Fock operator generated by the orbitals [math]\displaystyle{ \phi_j }[/math], and
- [math]\displaystyle{ \hat H^\text{core}(1) = -\frac{1}{2} \nabla^2_1 - \sum_\alpha \frac{Z_\alpha}{r_{1\alpha}} }[/math]
is the one-electron core Hamiltonian which includes kinetic energy plus attraction to all the nuclei (the "core") in the molecule, but omits interaction with other electrons.[15] Also
- [math]\displaystyle{ \hat J_j(1) }[/math]
is the Coulomb operator, defining the electron–electron repulsion energy due to each of the two electrons in the j-th orbital.[14] Finally,
- [math]\displaystyle{ \hat K_j(1) }[/math]
is the exchange operator, defining the electron exchange energy due to the antisymmetry of the total N-electron wave function.[14] This "exchange energy" operator [math]\displaystyle{ \hat K }[/math] is simply an artifact of the Slater determinant. Finding the Hartree–Fock one-electron wave functions is now equivalent to solving the eigenfunction equation
- [math]\displaystyle{ \hat F(1)\phi_i(1) = \epsilon_i \phi_i(1), }[/math]
where [math]\displaystyle{ \phi_i(1) }[/math] are a set of one-electron wave functions called the Hartree–Fock molecular orbitals.
Total energy
For an atom or molecule with a closed shell electron configuration, the total energy according to the Hartree-Fock method is
- [math]\displaystyle{ E_{HF} = 2 \sum_{i=1}^{N/2} \hat H^\text{core}_{ii} + \sum_{i=1}^{N/2} \sum_{j=1}^{N/2} [2\hat J_{ij} - \hat K_{ij}] + V_{nucl}. }[/math]
[math]\displaystyle{ \hat J_{ij} }[/math] and [math]\displaystyle{ \hat K_{ij} }[/math] are matrix elements of the Coulomb and exchange operators respectively, and
- [math]\displaystyle{ E_{HF} = 2 \sum_{i=1}^{N/2} \hat H^\text{core}_{ii} + \sum_{i=1}^{N/2} \sum_{j=1}^{N/2} [2\hat J_{ij} - \hat K_{ij}] + V_{nucl} }[/math][15] where [math]\displaystyle{ V_{nucl} }[/math] is the total electrostatic repulsion between all the nuclei in the molecule.
Linear combination of atomic orbitals
Typically, in modern Hartree–Fock calculations, the one-electron wave functions are approximated by a linear combination of atomic orbitals. These atomic orbitals are called Slater-type orbitals. Furthermore, it is very common for the "atomic orbitals" in use to actually be composed of a linear combination of one or more Gaussian-type orbitals, rather than Slater-type orbitals, in the interests of saving large amounts of computation time.
Various basis sets are used in practice, most of which are composed of Gaussian functions. In some applications, an orthogonalization method such as the Gram–Schmidt process is performed in order to produce a set of orthogonal basis functions. This can in principle save computational time when the computer is solving the Roothaan–Hall equations by converting the overlap matrix effectively to an identity matrix. However, in most modern computer programs for molecular Hartree–Fock calculations this procedure is not followed due to the high numerical cost of orthogonalization and the advent of more efficient, often sparse, algorithms for solving the generalized eigenvalue problem, of which the Roothaan–Hall equations are an example.
Numerical stability
Numerical stability can be a problem with this procedure and there are various ways of combatting this instability. One of the most basic and generally applicable is called F-mixing or damping. With F-mixing, once a single-electron wave function is calculated, it is not used directly. Instead, some combination of that calculated wave function and the previous wave functions for that electron is used, the most common being a simple linear combination of the calculated and immediately preceding wave function. A clever dodge, employed by Hartree, for atomic calculations was to increase the nuclear charge, thus pulling all the electrons closer together. As the system stabilised, this was gradually reduced to the correct charge. In molecular calculations a similar approach is sometimes used by first calculating the wave function for a positive ion and then to use these orbitals as the starting point for the neutral molecule. Modern molecular Hartree–Fock computer programs use a variety of methods to ensure convergence of the Roothaan–Hall equations.
Weaknesses, extensions, and alternatives
Of the five simplifications outlined in the section "Hartree–Fock algorithm", the fifth is typically the most important. Neglect of electron correlation can lead to large deviations from experimental results. A number of approaches to this weakness, collectively called post-Hartree–Fock methods, have been devised to include electron correlation to the multi-electron wave function. One of these approaches, Møller–Plesset perturbation theory, treats correlation as a perturbation of the Fock operator. Others expand the true multi-electron wave function in terms of a linear combination of Slater determinants—such as multi-configurational self-consistent field, configuration interaction, quadratic configuration interaction, and complete active space SCF (CASSCF). Still others (such as variational quantum Monte Carlo) modify the Hartree–Fock wave function by multiplying it by a correlation function ("Jastrow" factor), a term which is explicitly a function of multiple electrons that cannot be decomposed into independent single-particle functions.
An alternative to Hartree–Fock calculations used in some cases is density functional theory, which treats both exchange and correlation energies, albeit approximately. Indeed, it is common to use calculations that are a hybrid of the two methods—the popular B3LYP scheme is one such hybrid functional method. Another option is to use modern valence bond methods.
Software packages
For a list of software packages known to handle Hartree–Fock calculations, particularly for molecules and solids, see the list of quantum chemistry and solid state physics software.
See also
|
Related fields
|
Concepts
|
People
|
References
- ↑ Bruus, Henrik; Flensberg, Karsten (2014). Many-body quantum theory in condensed matter physics: an introduction (Corrected version ed.). Oxford New York: Oxford University Press. ISBN 9780198566335. https://www.phys.lsu.edu/~jarrell/COURSES/ADV_SOLID_HTML/Other_online_texts/Many-body%20quantum%20theory%20in%0Acondensed%20matter%20physics%0AHenrik%20Bruus%20and%20Karsten%20Flensberg.pdf.
- ↑ Froese Fischer, Charlotte (1987). "General Hartree-Fock program". Computer Physics Communications 43 (3): 355–365. doi:10.1016/0010-4655(87)90053-1. Bibcode: 1987CoPhC..43..355F.
- ↑ Abdulsattar, Mudar A. (2012). "SiGe superlattice nanocrystal infrared and Raman spectra: A density functional theory study". J. Appl. Phys. 111 (4): 044306–044306–4. doi:10.1063/1.3686610. Bibcode: 2012JAP...111d4306A.
- ↑ Hartree, D. R. (1928). "The Wave Mechanics of an Atom with a Non-Coulomb Central Field". Math. Proc. Camb. Philos. Soc. 24 (1): 111. doi:10.1017/S0305004100011920. Bibcode: 1928PCPS...24..111H.
- ↑ Slater, J. C. (1928). "The Self Consistent Field and the Structure of Atoms". Phys. Rev. 32 (3): 339–348. doi:10.1103/PhysRev.32.339. Bibcode: 1928PhRv...32..339S.
- ↑ Gaunt, J. A. (1928). "A Theory of Hartree's Atomic Fields". Math. Proc. Camb. Philos. Soc. 24 (2): 328–342. doi:10.1017/S0305004100015851. Bibcode: 1928PCPS...24..328G.
- ↑ Slater, J. C. (1930). "Note on Hartree's Method". Phys. Rev. 35 (2): 210–211. doi:10.1103/PhysRev.35.210.2. Bibcode: 1930PhRv...35..210S.
- ↑ Fock, V. A. (1930). "Näherungsmethode zur Lösung des quantenmechanischen Mehrkörperproblems" (in de). Z. Phys. 61 (1): 126–148. doi:10.1007/BF01340294. Bibcode: 1930ZPhy...61..126F. Fock, V. A. (1930). ""Selfconsistent field" mit Austausch für Natrium" (in de). Z. Phys. 62 (11): 795–805. doi:10.1007/BF01330439. Bibcode: 1930ZPhy...62..795F.
- ↑ Hartree, D. R.; Hartree, W. (1935). "Self-consistent field, with exchange, for beryllium". Proc. R. Soc. Lond. A 150 (869): 9. doi:10.1098/rspa.1935.0085. Bibcode: 1935RSPSA.150....9H.
- ↑ Slater, J. C. (1951). "A Simplification of the Hartree-Fock Method". Physical Review 81 (3): 385–390. doi:10.1103/PhysRev.81.385. Bibcode: 1951PhRv...81..385S. https://link.aps.org/doi/10.1103/PhysRev.81.385.
- ↑ Hinchliffe, Alan (2000). Modelling Molecular Structures (2nd ed.). Baffins Lane, Chichester, West Sussex PO19 1UD, England: John Wiley & Sons Ltd. p. 186. ISBN 0-471-48993-X.
- ↑ Szabo, A.; Ostlund, N. S. (1996). Modern Quantum Chemistry. Mineola, New York: Dover Publishing. ISBN 0-486-69186-1.
- ↑ A. J. Stone (1996), The Theory of Intermolecular Forces, Oxford: Clarendon Press.
- ↑ 14.0 14.1 14.2 Levine, Ira N. (1991). Quantum Chemistry (4th ed.). Englewood Cliffs, New Jersey: Prentice Hall. p. 403. ISBN:0-205-12770-3.
- ↑ 15.0 15.1 Levine, Ira N. (1991). Quantum Chemistry (4th ed.). Englewood Cliffs, New Jersey: Prentice Hall. p. 402-3. ISBN:0-205-12770-3.
Sources
- Levine, Ira N. (1991). Quantum Chemistry (4th ed.). Englewood Cliffs, New Jersey: Prentice Hall. pp. 455–544. ISBN 0-205-12770-3.
- Cramer, Christopher J. (2002). Essentials of Computational Chemistry. Chichester: John Wiley & Sons, Ltd.. pp. 153–189. ISBN 0-471-48552-7.
- Szabo, A.; Ostlund, N. S. (1996). Modern Quantum Chemistry. Mineola, New York: Dover Publishing. ISBN 0-486-69186-1.
External links
- The Wave Mechanics of an Atom with a Non-Coulomb Central Field. Part II. Some Results and Discussion by D. R. Hartree, Mathematical Proceedings of the Cambridge Philosophical Society, Volume 24, 111–132, January 1928
- An Introduction to Hartree-Fock Molecular Orbital Theory by C. David Sherrill (June 2000)
- Mean-Field Theory: Hartree-Fock and BCS in E. Pavarini, E. Koch, J. van den Brink, and G. Sawatzky: Quantum materials: Experiments and Theory, Jülich 2016, ISBN:978-3-95806-159-0
redundant -->
redundant -->
 |