Physics:Magnetic current
| Part of a series of articles about |
| Electromagnetism |
|---|
 |
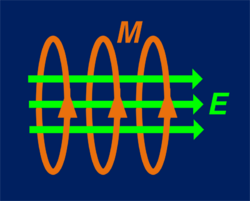
Magnetic current is, nominally, a current composed of fictitious moving magnetic monopoles. It has the unit volt. The usual symbol for magnetic current is [math]\displaystyle{ k }[/math], which is analogous to [math]\displaystyle{ i }[/math] for electric current. Magnetic currents produce an electric field analogously to the production of a magnetic field by electric currents. Magnetic current density, which has the unit V/m2 (volt per square meter), is usually represented by the symbols [math]\displaystyle{ \mathfrak{M}^\text{t} }[/math] and [math]\displaystyle{ \mathfrak{M}^\text{i} }[/math]. The superscripts indicate total and impressed magnetic current density.[1] The impressed currents are the energy sources. In many useful cases, a distribution of electric charge can be mathematically replaced by an equivalent distribution of magnetic current. This artifice can be used to simplify some electromagnetic field problems.[lower-alpha 1][lower-alpha 2] It is possible to use both electric current densities and magnetic current densities in the same analysis.[4]:138
The direction of the electric field produced by magnetic currents is determined by the left-hand rule (opposite direction as determined by the right-hand rule) as evidenced by the negative sign in the equation[1] [math]\displaystyle{ \nabla \times \mathcal{E} = -\mathfrak{M}^\text{t} . }[/math]
Magnetic displacement current
Magnetic displacement current or more properly the magnetic displacement current density is the familiar term ∂B/∂t[lower-alpha 3][lower-alpha 4][lower-alpha 5] It is one component of [math]\displaystyle{ \mathfrak{M}^\text{t} }[/math].[1][2] [math]\displaystyle{ \mathfrak{M}^\text{t} = \frac {\partial B} {\partial t} + \mathfrak{M}^\text{i} . }[/math] where
- [math]\displaystyle{ \mathfrak{M}^\text{t} }[/math] is the total magnetic current.
- [math]\displaystyle{ \mathfrak{M}^\text{i} }[/math] is the impressed magnetic current (energy source).
Electric vector potential
The electric vector potential, F, is computed from the magnetic current density, [math]\displaystyle{ \mathfrak{M}^\text{i} }[/math], in the same way that the magnetic vector potential, A, is computed from the electric current density.[1]:100 [4]:138 [3]:468 Examples of use include finite diameter wire antennas and transformers.[5]
magnetic vector potential: [math]\displaystyle{ \mathbf A (\mathbf r , t) = \frac{\mu_0}{4\pi}\int_\Omega \frac{\mathbf J (\mathbf r' , t')}{|\mathbf r - \mathbf r'|}\, \mathrm{d}^3\mathbf r'\,. }[/math]
electric vector potential: [math]\displaystyle{ \mathbf F (\mathbf r , t) = \frac{\varepsilon_0}{4\pi}\int_\Omega \frac{\mathfrak{M}^\text{i} (\mathbf r' , t')}{|\mathbf r - \mathbf r'|}\, \mathrm{d}^3\mathbf r'\,, }[/math] where F at point [math]\displaystyle{ \mathbf r }[/math] and time [math]\displaystyle{ t }[/math] is calculated from magnetic currents at distant position [math]\displaystyle{ \mathbf r' }[/math] at an earlier time [math]\displaystyle{ t' }[/math]. The location [math]\displaystyle{ \mathbf r' }[/math] is a source point within volume Ω that contains the magnetic current distribution. The integration variable, [math]\displaystyle{ \mathrm{d}^3\mathbf r' }[/math], is a volume element around position [math]\displaystyle{ \mathbf r' }[/math]. The earlier time [math]\displaystyle{ t' }[/math] is called the retarded time, and calculated as [math]\displaystyle{ t' = t - \frac{|\mathbf r - \mathbf r'|}{c}. }[/math]
Retarded time accounts for the accounts for the time required for electromagnetic effects to propagate from point [math]\displaystyle{ \mathbf r' }[/math] to point [math]\displaystyle{ \mathbf r }[/math].
Phasor form
When all the functions of time are sinusoids of the same frequency, the time domain equation can be replaced with a frequency domain equation. Retarded time is replaced with a phase term. [math]\displaystyle{ \mathbf F (\mathbf r ) = \frac{\varepsilon_0}{4\pi} \int_\Omega \frac{\mathfrak{M}^\text{i} (\mathbf{r}) e^{-jk |\mathbf{r} - \mathbf r'|}}{|\mathbf r - \mathbf r'|}\, \mathrm{d}^3\mathbf r'\,, }[/math] where [math]\displaystyle{ \mathbf F }[/math] and [math]\displaystyle{ \mathfrak{M}^\text{i} }[/math] are phasor quantities and [math]\displaystyle{ k }[/math] is the wave number.
Magnetic frill generator
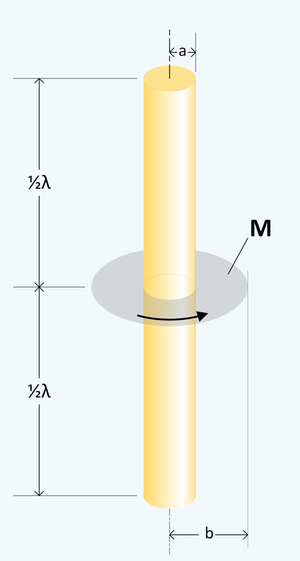
A distribution of magnetic current, commonly called a magnetic frill generator, may be used to replace the driving source and feed line in the analysis of a finite diameter dipole antenna.[4]:447–450 The voltage source and feed line impedance are subsumed into the magnetic current density. In this case, the magnetic current density is concentrated in a two dimensional surface so the units of [math]\displaystyle{ \mathfrak{M}^\text{i} }[/math] are volts per meter.
The inner radius of the frill is the same as the radius of the dipole. The outer radius is chosen so that [math]\displaystyle{ Z_\text{L} = Z_0 \ln\left( \frac b a\right), }[/math] where
- [math]\displaystyle{ Z_\text{L} }[/math] = impedance of the feed transmission line (not shown).
- [math]\displaystyle{ Z_0 }[/math] = impedance of free space.
The equation is the same as the equation for the impedance of a coaxial cable. However, a coaxial cable feed line is not assumed and not required.
The amplitude of the magnetic current density phasor is given by: [math]\displaystyle{ \mathfrak{M}^\text{i} = \frac k \rho }[/math] with [math]\displaystyle{ a \le \rho \le b. }[/math] where
- [math]\displaystyle{ \rho }[/math] = radial distance from the axis.
- [math]\displaystyle{ k = \frac {V_\text{s}} {\ln\left( \frac b a\right)} }[/math].
- [math]\displaystyle{ V_\text{s} }[/math] = magnitude of the source voltage phasor driving the feed line.
See also
Notes
- ↑ "For some electromagnetic problems, their solution can often be aided by the introduction of equivalent impressed electric and magnetic current densities."[2]
- ↑ "there are many other problems where the use of fictitious magnetic currents and charges is very helpful."[3]
- ↑ "Because of the symmetry of Maxwell's equations, the ∂B/∂t term ... has been designated as a magnetic displacement current density."[2]
- ↑ "interpreted as ... magnetic displacement current ..."[3]
- ↑ "it also is convenient to consider the term ∂B/∂t as a magnetic displacement current density."[1]
References
- ↑ 1.0 1.1 1.2 1.3 1.4 Harrington, Roger F. (1961), Time-Harmonic Electromagnetic Fields, McGraw-Hill, pp. 7–8, ISBN 0-07-026745-6
- ↑ 2.0 2.1 2.2 Balanis, Constantine A. (2012), Advanced Engineering Electromagnetics, John Wiley, pp. 2–3, ISBN 978-0-470-58948-9
- ↑ 3.0 3.1 3.2 Jordan, Edward; Balmain, Keith G. (1968), Electromagnetic Waves and Radiating Systems (2nd ed.), Prentice-Hall, p. 466
- ↑ 4.0 4.1 4.2 Balanis, Constantine A. (2005), Antenna Theory (third ed.), John Wiley, ISBN 047166782X
- ↑ Kulkarni, S. V.; Khaparde, S. A. (2004), Transformer Engineering: Design and Practice (third ed.), CRC Press, pp. 179–180, ISBN 0824756533
 |