Physics:Reaction mechanism
In chemistry, a reaction mechanism is the step by step sequence of elementary reactions by which overall chemical reaction occurs.[1]
A chemical mechanism is a theoretical conjecture that tries to describe in detail what takes place at each stage of an overall chemical reaction. The detailed steps of a reaction are not observable in most cases. The conjectured mechanism is chosen because it is thermodynamically feasible and has experimental support in isolated intermediates (see next section) or other quantitative and qualitative characteristics of the reaction. It also describes each reactive intermediate, activated complex, and transition state, which bonds are broken (and in what order), and which bonds are formed (and in what order). A complete mechanism must also explain the reason for the reactants and catalyst used, the stereochemistry observed in reactants and products, all products formed and the amount of each.
The electron or arrow pushing method is often used in illustrating a reaction mechanism; for example, see the illustration of the mechanism for benzoin condensation in the following examples section.
A reaction mechanism must also account for the order in which molecules react. Often what appears to be a single-step conversion is in fact a multistep reaction.
Reaction intermediates
Reaction intermediates are chemical species, often unstable and short-lived (however sometimes can be isolated), which are not reactants or products of the overall chemical reaction, but are temporary products and/or reactants in the mechanism's reaction steps. Reaction intermediates are often free radicals or ions.
The kinetics (relative rates of the reaction steps and the rate equation for the overall reaction) are explained in terms of the energy needed for the conversion of the reactants to the proposed transition states (molecular states that correspond to maxima on the reaction coordinates, and to saddle points on the potential energy surface for the reaction).
Chemical kinetics
Information about the mechanism of a reaction is often provided by the use of chemical kinetics to determine the rate equation and the reaction order in each reactant.[2]
Consider the following reaction for example:
- CO + NO2 → CO2 + NO
In this case, experiments have determined that this reaction takes place according to the rate law [math]\displaystyle{ r = k[NO_2]^2 }[/math]. This form suggests that the rate-determining step is a reaction between two molecules of NO2. A possible mechanism for the overall reaction that explains the rate law is:
- 2 NO2 → NO3 + NO (slow)
- NO3 + CO → NO2 + CO2 (fast)
Each step is called an elementary step, and each has its own rate law and molecularity. The elementary steps should add up to the original reaction. (Meaning, if we were to cancel out all the molecules that appear on both sides of the reaction, we would be left with the original reaction.)
When determining the overall rate law for a reaction, the slowest step is the step that determines the reaction rate. Because the first step (in the above reaction) is the slowest step, it is the rate-determining step. Because it involves the collision of two NO2 molecules, it is a bimolecular reaction with a rate [math]\displaystyle{ r }[/math] which obeys the rate law [math]\displaystyle{ r = k[NO_{2}(t)]^2 }[/math].
Other reactions may have mechanisms of several consecutive steps. In organic chemistry, the reaction mechanism for the benzoin condensation, put forward in 1903 by A. J. Lapworth, was one of the first proposed reaction mechanisms.

A chain reaction is an example of a complex mechanism, in which the propagation steps form a closed cycle. In a chain reaction, the intermediate produced in one step generates an intermediate in another step. Intermediates are called chain carriers. Sometimes, the chain carriers are radicals, they can be ions as well. In nuclear fission they are neutrons.
Chain reactions have several steps, which may include:[3]
- Chain initiation: this can be by thermolysis (heating the molecules) or photolysis (absorption of light) leading to the breakage of a bond.
- Propagation: a chain carrier makes another carrier.
- Branching: one carrier makes more than one carrier.
- Retardation: a chain carrier may react with a product reducing the rate of formation of the product. It makes another chain carrier, but the product concentration is reduced.
- Chain termination: radicals combine and the chain carriers are lost.
- Inhibition: chain carriers are removed by processes other than termination, such as by forming radicals.
Even though all these steps can appear in one chain reaction, the minimum necessary ones are Initiation, propagation, and termination.
An example of a simple chain reaction is the thermal decomposition of acetaldehyde (CH3CHO) to methane (CH4) and carbon monoxide (CO). The experimental reaction order is 3/2,[4] which can be explained by a Rice-Herzfeld mechanism.[5]
This reaction mechanism for acetaldehyde has 4 steps with rate equations for each step :
- Initiation : CH3CHO → •CH3 + •CHO (Rate=k1 [CH3CHO])
- Propagation: CH3CHO + •CH3 → CH4 + CH3CO• (Rate=k2 [CH3CHO][•CH3])
- Propagation: CH3CO• → •CH3 + CO (Rate=k3 [CH3CO•])
- Termination: •CH3 + •CH3 → CH3CH3 (Rate=k4 [•CH3]2)
For the overall reaction, the rates of change of the concentration of the intermediates •CH3 and CH3CO• are zero, according to the steady-state approximation, which is used to account for the rate laws of chain reactions.[6]
d[•CH3]/dt = k1[CH3CHO] – k2[•CH3][CH3CHO] + k3[CH3CO•] - 2k4[•CH3]2 = 0
and d[CH3CO•]/dt = k2[•CH3][CH3CHO] – k3[CH3CO•] = 0
The sum of these two equations is k1[CH3CHO] – 2 k4[•CH3]2 = 0. This may be solved to find the steady-state concentration of •CH3 radicals as [•CH3] = (k1 / 2k4)1/2 [CH3CHO]1/2.
It follows that the rate of formation of CH4 is d[CH4]/dt = k2[•CH3][CH3CHO] = k2 (k1 / 2k4)1/2 [CH3CHO]3/2
Thus the mechanism explains the observed rate expression, for the principal products CH4 and CO. The exact rate law may be even more complicated, there are also minor products such as acetone (CH3COCH3) and propanal (CH3CH2CHO).
Other experimental methods to determine mechanism
Many experiments that suggest the possible sequence of steps in a reaction mechanism have been designed, including:
- measurement of the effect of temperature (Arrhenius equation) to determine the activation energy[7]
- spectroscopic observation of reaction intermediates
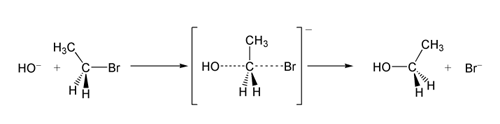
- determination of the stereochemistry of products, for example in nucleophilic substitution reactions[8]
- measurement of the effect of isotopic substitution on the reaction rate[9]
- for reactions in solution, measurement of the effect of pressure on the reaction rate to determine the volume change on formation of the activated complex[10][11]
- for reactions of ions in solution, measurement of the effect of ionic strength on the reaction rate[12][13]
- direct observation of the activated complex by pump-probe spectroscopy[14]
- infrared chemiluminescence to detect vibrational excitation in the products[15][16]
- electrospray ionization mass spectrometry.[17]
- crossover experiments.[18]
Theoretical modeling
A correct reaction mechanism is an important part of accurate predictive modeling. For many combustion and plasma systems, detailed mechanisms are not available or require development.
Even when information is available, identifying and assembling the relevant data from a variety of sources, reconciling discrepant values and extrapolating to different conditions can be a difficult process without expert help. Rate constants or thermochemical data are often not available in the literature, so computational chemistry techniques or group additivity methods must be used to obtain the required parameters.
Computational chemistry methods can also be used to calculate potential energy surfaces for reactions and determine probable mechanisms.[19]
Molecularity
Molecularity in chemistry is the number of colliding molecular entities that are involved in a single reaction step.
- A reaction step involving one molecular entity is called unimolecular.
- A reaction step involving two molecular entities is called bimolecular.
- A reaction step involving three molecular entities is called trimolecular or termolecular.
In general, reaction steps involving more than three molecular entities do not occur, because is statistically improbable in terms of Maxwell distribution to find such a transition state.
See also
- Organic reactions by mechanism
- Nucleophilic acyl substitution
- Neighbouring group participation
- Finkelstein reaction
- Lindemann mechanism
- Electrochemical reaction mechanism
- Nucleophilic abstraction
References
- ↑ March, Jerry (1985), Advanced Organic Chemistry: Reactions, Mechanisms, and Structure (3rd ed.), New York: Wiley, ISBN 0-471-85472-7
- ↑ Espenson, James H. Chemical Kinetics and Reaction Mechanisms (2nd ed., McGraw-Hill, 2002) chap.6, Deduction of Reaction Mechanisms ISBN:0-07-288362-6
- ↑ Bäckström, Hans L. J. (1 June 1927). "The chain-reaction theory of negative catalysis". Journal of the American Chemical Society 49 (6): 1460–1472. doi:10.1021/ja01405a011. https://pubs.acs.org/doi/abs/10.1021/ja01405a011. Retrieved 20 January 2021.
- ↑ Laidler K.J. and Meiser J.H., Physical Chemistry (Benjamin/Cummings 1982) p.416-417 ISBN:0-8053-5682-7
- ↑ Atkins and de Paula p.830-1
- ↑ Atkins P and de Paula J, Physical Chemistry (8th ed., W.H. Freeman 2006) p.812 ISBN:0-7167-8759-8
- ↑ Espenson p.156-160
- ↑ Morrison R.T. and Boyd R.N. Organic Chemistry (4th ed., Allyn and Bacon 1983) p.216-9 and p.228-231, ISBN:0-205-05838-8
- ↑ Atkins P and de Paula J, Physical Chemistry (8th ed., W.H. Freeman 2006) p.816-8 ISBN:0-7167-8759-8
- ↑ Moore J.W. and Pearson R.G. Kinetics and Mechanism (3rd ed., John Wiley 1981) p.276-8 ISBN:0-471-03558-0
- ↑ Laidler K.J. and Meiser J.H., Physical Chemistry (Benjamin/Cummings 1982) p.389-392 ISBN:0-8053-5682-7
- ↑ Atkins and de Paula p.884-5
- ↑ Laidler and Meiser p.388-9
- ↑ Atkins and de Paula p.892-3
- ↑ Atkins and de Paula p.886
- ↑ Laidler and Meiser p.396-7
- ↑ Investigation of chemical reactions in solution using API-MS Leonardo Silva Santos, Larissa Knaack, Jurgen O. Metzger Int. J. Mass Spectrom.; 2005; 246 pp 84 - 104; (Review) doi:10.1016/j.ijms.2005.08.016
- ↑ Espenson p.112
- ↑ Atkins and de Paula p.887-891
L.G.WADE, ORGANIC CHEMISTRY 7TH ED, 2010
External links
 |

