Physics:Demagnetizing field
| Part of a series of articles about |
| Electromagnetism |
|---|
 |
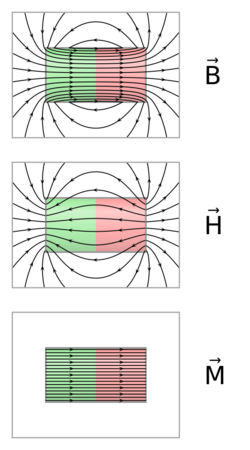
The demagnetizing field, also called the stray field (outside the magnet), is the magnetic field (H-field)[1] generated by the magnetization in a magnet. The total magnetic field in a region containing magnets is the sum of the demagnetizing fields of the magnets and the magnetic field due to any free currents or displacement currents. The term demagnetizing field reflects its tendency to act on the magnetization so as to reduce the total magnetic moment. It gives rise to shape anisotropy in ferromagnets with a single magnetic domain and to magnetic domains in larger ferromagnets.
The demagnetizing field of an arbitrarily shaped object requires a numerical solution of Poisson's equation even for the simple case of uniform magnetization. For the special case of ellipsoids (including infinite cylinders) the demagnetization field is linearly related to the magnetization by a geometry dependent constant called the demagnetizing factor. Since the magnetization of a sample at a given location depends on the total magnetic field at that point, the demagnetization factor must be used in order to accurately determine how a magnetic material responds to a magnetic field. (See magnetic hysteresis.)
Magnetostatic principles
Maxwell's equations
In general the demagnetizing field is a function of position H(r). It is derived from the magnetostatic equations for a body with no electric currents.[2] These are Ampère's law
-
[math]\displaystyle{ \nabla\times\mathbf{H} = 0, }[/math][3]
()
and Gauss's law
-
[math]\displaystyle{ \nabla\cdot\mathbf{B} = 0. }[/math][4]
()
The magnetic field and flux density are related by[5][6]
-
[math]\displaystyle{ \mathbf{B} = \mu_0 \left(\mathbf{M}+\mathbf{H}\right), }[/math][7]
()
where [math]\displaystyle{ \mu_0 }[/math] is the permeability of vacuum and M is the magnetisation.
The magnetic potential
The general solution of the first equation can be expressed as the gradient of a scalar potential U(r):
Inside the magnetic body, the potential Uin is determined by substituting (3) and (4) in (2):
-
[math]\displaystyle{ \nabla^2 U_\text{in} = \nabla\cdot\mathbf{M}. }[/math][8]
()
Outside the body, where the magnetization is zero,
-
[math]\displaystyle{ \nabla^2 U_\text{out} = 0. }[/math]
()
At the surface of the magnet, there are two continuity requirements:[5]
- The component of H parallel to the surface must be continuous (no jump in value at the surface).
- The component of B perpendicular to the surface must be continuous.
This leads to the following boundary conditions at the surface of the magnet:
-
[math]\displaystyle{ \begin{align} U_\text{in} &= U_\text{out}\\ \frac{\partial U_\text{in}}{\partial n} &= \frac{\partial U_\text{out}}{\partial n} + \mathbf{M}\cdot\mathbf{n}. \end{align} }[/math]
()
Here n is the surface normal and [math]\displaystyle{ \partial/ \partial n }[/math] is the derivative with respect to distance from the surface.[9]
The outer potential Uout must also be regular at infinity: both |r U| and |r2 U| must be bounded as r goes to infinity. This ensures that the magnetic energy is finite.[10] Sufficiently far away, the magnetic field looks like the field of a magnetic dipole with the same moment as the finite body.
Uniqueness of the demagnetizing field
Any two potentials that satisfy equations (5), (6) and (7), along with regularity at infinity, have identical gradients. The demagnetizing field Hd is the gradient of this potential (equation 4).
Energy
The energy of the demagnetizing field is completely determined by an integral over the volume V of the magnet:
-
[math]\displaystyle{ E = -\frac{\mu_0}{2}\int_\text{magnet} \mathbf{M}\cdot\mathbf{H}_\text{d} dV }[/math]
()
Suppose there are two magnets with magnetizations M1 and M2. The energy of the first magnet in the demagnetizing field Hd(2) of the second is
-
[math]\displaystyle{ E =\mu_0 \int_\text{magnet 1} \mathbf{M}_1\cdot\mathbf{H}_\text{d}^{(2)} dV. }[/math]
()
The reciprocity theorem states that[9]
-
[math]\displaystyle{ \int_\text{magnet 1} \mathbf{M}_1\cdot\mathbf{H}_\text{d}^{(2)} dV = \int_\text{magnet 2} \mathbf{M}_2\cdot\mathbf{H}_\text{d}^{(1)} dV. }[/math]
()
Magnetic charge and the pole-avoidance principle
Formally, the solution of the equations for the potential is
-
[math]\displaystyle{ U(\mathbf{r}) = -\frac{1}{4\pi}\int_\text{volume} \frac{\nabla'\cdot\mathbf{M\left(r'\right)}}{|\mathbf{r}-\mathbf{r}'|}dV' + \frac{1}{4\pi}\int_\text{surface} \frac{\mathbf{n}\cdot\mathbf{M\left(r'\right)}}{|\mathbf{r}-\mathbf{r}'|}dS', }[/math]
()
where r′ is the variable to be integrated over the volume of the body in the first integral and the surface in the second, and ∇′ is the gradient with respect to this variable.[9]
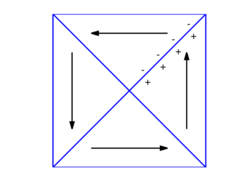
Qualitatively, the negative of the divergence of the magnetization − ∇ · M (called a volume pole) is analogous to a bulk bound electric charge in the body while n · M (called a surface pole) is analogous to a bound surface electric charge. Although the magnetic charges do not exist, it can be useful to think of them in this way. In particular, the arrangement of magnetization that reduces the magnetic energy can often be understood in terms of the pole-avoidance principle, which states that the magnetization tries to reduce the poles as much as possible.[9]
Effect on magnetization
Single domain
One way to remove the magnetic poles inside a ferromagnet is to make the magnetization uniform. This occurs in single-domain ferromagnets. This still leaves the surface poles, so division into domains reduces the poles further[clarification needed]. However, very small ferromagnets are kept uniformly magnetized by the exchange interaction.
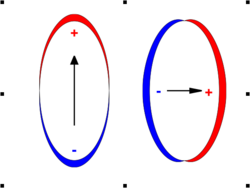
The concentration of poles depends on the direction of magnetization (see the figure). If the magnetization is along the longest axis, the poles are spread across a smaller surface, so the energy is lower. This is a form of magnetic anisotropy called shape anisotropy.
Multiple domains
If the ferromagnet is large enough, its magnetization can divide into domains. It is then possible to have the magnetization parallel to the surface. Within each domain the magnetization is uniform, so there are no volume poles, but there are surface poles at the interfaces (domain walls) between domains. However, these poles vanish if the magnetic moments on each side of the domain wall meet the wall at the same angle (so that the components n · M are the same but opposite in sign). Domains configured this way are called closure domains.
Demagnetizing factor
An arbitrarily shaped magnetic object has a total magnetic field that varies with location inside the object and can be quite difficult to calculate. This makes it very difficult to determine the magnetic properties of a material such as, for instance, how the magnetization of a material varies with the magnetic field. For a uniformly magnetized sphere in a uniform magnetic field H0 the internal magnetic field H is uniform:
-
[math]\displaystyle{ \mathbf{H} = \mathbf{H}_0 - \gamma \mathbf{M}_0, }[/math]
()
where M0 is the magnetization of the sphere and γ is called the demagnetizing factor, which assumes values between 0 and 1, and equals 1/3 for a sphere in SI units.[5][6][11] Note that in cgs units γ assumes values between 0 and 4π.
This equation can be generalized to include ellipsoids having principal axes in x, y, and z directions such that each component has a relationship of the form:[6]
-
[math]\displaystyle{ H_k=(H_0)_k - \gamma_k (M_0)_k, \qquad k = x,y,z. }[/math]
()
Other important examples are an infinite plate (an ellipsoid with two of its axes going to infinity) which has γ = 1 (SI units) in a direction normal to the plate and zero otherwise and an infinite cylinder (an ellipsoid with one of its axes tending toward infinity with the other two being the same) which has γ = 0 along its axis and 1/2 perpendicular to its axis.[12] The demagnetizing factors are the principal values of the depolarization tensor, which gives both the internal and external values of the fields induced in ellipsoidal bodies by applied electric or magnetic fields.[13] [14] [15]
Notes and references
- ↑ In this article the term 'magnetic field' is used for the magnetic 'H field' while 'magnetic flux density' is used for the magnetic 'B-field'.
- ↑ If there are electric currents in the system, they can be calculated separately and added to the solutions of these equations.
- ↑ In words, the curl of the magnetic field is zero.
- ↑ In words, the divergence of the magnetic flux density is zero.
- ↑ 5.0 5.1 5.2 5.3 Jackson 1975, chapter 5
- ↑ 6.0 6.1 6.2 6.3 Nayfeh & Brussel 1985, chapter 9
- ↑ SI units are used in this article.
- ↑ The symbol ∇2 ≡ ∇ · ∇ is the Laplace operator.
- ↑ 9.0 9.1 9.2 9.3 Aharoni 1996, chapter 6
- ↑ Brown 1962
- ↑ Griffiths 1999, chapter 6
- ↑ For tables or equations for the magnetizing factors of the general ellipsoid see Osborn, J. A. (1945). "Demagnetizing Factors of the General Ellipsoid". Physical Review 67 (11–12): 351–7. doi:10.1103/PhysRev.67.351. Bibcode: 1945PhRv...67..351O. http://www.cmap.polytechnique.fr/~alouges/coursm2/Osborn.pdf.
- ↑ Solivérez, C. E. (1981). "Magnetostatics of Anisotropic Ellipsoidal Bodies". IEEE Transactions on Magnetics 17 (3): 1363–4. doi:10.1109/TMAG.1981.1061200. Bibcode: 1981ITM....17.1363S. https://independent.academia.edu/Csoliverez/Papers/1600497/Magnetostatics_of_anisotropic_ellipsoids.
- ↑ Di Fratta, G. (2016). "The Newtonian Potential and the Demagnetizing Factors of the General Ellipsoid". Proc. R. Soc. A 472 (2190): 20160197. doi:10.1098/rspa.2016.0197. PMID 27436988. Bibcode: 2016RSPSA.47260197D.
- ↑ Solivérez, C. E. (2016). Electrostatics and Magnetostatics of Polarized Ellipsoidal Bodies: The Depolarization Tensor Method. Free Scientific Information. ISBN 978-987-28304-0-3. http://cyt-ar.com.ar/cyt-ar/index.php/Archivo:Depolarization_Tensor_Method_2nd_edition.pdf.
Further reading
- Aharoni, Amikam (1996). Introduction to the Theory of Ferromagnetism. Clarendon Press. ISBN 978-0-19-851791-7. https://archive.org/details/introductiontoth00ahar.
- Brown, William Fuller Jr. (1962). Magnetostatic Principles in Ferromagnetism. Interscience.
- Griffiths, David J. (1999). Introduction to Electrodynamics (third ed.). Prentice Hall. ISBN 978-0-13-805326-0. https://archive.org/details/introductiontoel00grif_0.
- Jackson, John David (1975). Classical Electrodynamics (Second ed.). John Wiley & Sons. ISBN 978-0-471-43132-9. https://archive.org/details/classicalelectro00jack_0.
- Nayfeh, Munir H.; Brussel, Morton K. (1985). Electricity and Magnetism. John Wiley & Sons. ISBN 978-0-471-87681-6.
 |