Astronomy:Subsolar point
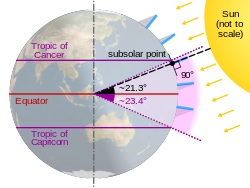
The subsolar point on a planet is the point at which its Sun is perceived to be directly overhead (at the zenith);[1] that is, where the Sun's rays strike the planet exactly perpendicular to its surface. It can also mean the point closest to the Sun on an astronomical object, even though the Sun might not be visible.
To an observer on a planet with an orientation and rotation similar to those of Earth, the subsolar point will appear to move westward with a speed of 1600 km/h, completing one circuit around the globe each day, approximately moving along the equator. However, it will also move north and south between the tropics over the course of a year, so will appear to spiral like a helix.
The subsolar point contacts the Tropic of Cancer on the June solstice and the Tropic of Capricorn on the December solstice. The subsolar point crosses the Equator on the March and September equinoxes.
Coordinates of the subsolar point
The subsolar point moves constantly on the surface of the Earth, but for any given time, its coordinates, or latitude and longitude, can be calculated as follows:[2]
[math]\displaystyle{ \phi_{s} = \delta, }[/math] [math]\displaystyle{ \lambda_{s} = -15(T_\mathrm{GMT}-12+E_\mathrm{min}/60). }[/math]
where
- [math]\displaystyle{ \phi_{s} }[/math] is the latitude of the subsolar point in degrees,
- [math]\displaystyle{ \lambda_{s} }[/math] is the longitude of the subsolar point in degrees,
- [math]\displaystyle{ \delta }[/math] is the declination of the Sun in degrees,
- [math]\displaystyle{ T_\mathrm{GMT} }[/math] is the Greenwich Mean Time or UTC, in decimal hours since 00:00:00 UTC on the relevant date
- [math]\displaystyle{ E_\mathrm{min} }[/math] is the equation of time in minutes.
Observation in specific locations

- Qibla observation by shadows, when the subsolar point passes through the Ka'bah in Saudi Arabia, allowing the Muslim sacred direction to be found by observing shadows.
- When the point passes through Hawaii, which is the only United States in which this happens, the event is known as Lahaina Noon.[3]
See also
- Subsatellite point
References
- ↑ Ian Ridpath, ed (1997). "subsolar point". A Dictionary of Astronomy. Oxford; New York: Oxford University Press. ISBN 0-19-211596-0. https://archive.org/details/dictionaryofastr0000unse. "The point on the Earth, or other body, at which the Sun is directly overhead at a particular time.".
- ↑ Zhang, Taiping; Stackhouse, Paul W.; MacPherson, Bradley; Mikovitz, J. Colleen (2021). "A solar azimuth formula that renders circumstantial treatment unnecessary without compromising mathematical rigor: Mathematical setup, application and extension of a formula based on the subsolar point and atan2 function". Renewable Energy 172: 1333–1340. doi:10.1016/j.renene.2021.03.047. https://doi.org/10.1016/j.renene.2021.03.047.
- ↑ Nancy Alima Ali (May 11, 2010). "Noon sun not directly overhead everywhere". Honolulu Star-Bulletin. http://archives.starbulletin.com/content/20100511_Noon_sun_not_directly_overhead_everywhere/. Retrieved November 12, 2010.
External links
- Day and Night World Map (shows location of subsolar point for any user-specified time)
 |