Levi-Civita connection

Short description: Affine connection on the tangent bundle of a manifold

In Riemannian or pseudo-Riemannian geometry (in particular the Lorentzian geometry of general relativity), the Levi-Civita connection is the unique affine connection on the tangent bundle of a manifold (i.e. affine connection) that preserves the (pseudo-)Riemannian metric and is torsion-free.

The fundamental theorem of Riemannian geometry states that there is a unique connection which satisfies these properties.

In the theory of Riemannian and pseudo-Riemannian manifolds the term covariant derivative is often used for the Levi-Civita connection. The components (structure coefficients) of this connection with respect to a system of local coordinates are called Christoffel symbols.

History

The Levi-Civita connection is named after Tullio Levi-Civita, although originally "discovered" by Elwin Bruno Christoffel. Levi-Civita, along with Gregorio Ricci-Curbastro, used Christoffel's symbols to define the notion of parallel transport and explore the relationship of parallel transport with the curvature, thus developing the modern notion of holonomy.

In 1869, Christoffel discovered that the components of the intrinsic derivative of a vector field, upon changing the coordinate system, transform as the components of a contravariant vector. This discovery was the real beginning of tensor analysis.

In 1906, L. E. J. Brouwer was the first mathematician to consider the parallel transport of a vector for the case of a space of constant curvature.

In 1917, Levi-Civita pointed out its importance for the case of a hypersurface immersed in a Euclidean space, i.e., for the case of a Riemannian manifold embedded in a "larger" ambient space. He interpreted the intrinsic derivative in the case of an embedded surface as the tangential component of the usual derivative in the ambient affine space. The Levi-Civita notions of intrinsic derivative and parallel displacement of a vector along a curve make sense on an abstract Riemannian manifold, even though the original motivation relied on a specific embedding [math]\displaystyle{ M^n \subset \mathbf{R}^{n(n+1)/2}. }[/math]

In 1918, independently of Levi-Civita, Jan Arnoldus Schouten obtained analogous results. In the same year, Hermann Weyl generalized Levi-Civita's results.

Notation

• (M, g) denotes a Riemannian or pseudo-Riemannian manifold.
• TM is the tangent bundle of M.
• g is the Riemannian or pseudo-Riemannian metric of M.
• X, Y, Z are smooth vector fields on M, i. e. smooth sections of TM.
• [X, Y] is the Lie bracket of X and Y. It is again a smooth vector field.

The metric g can take up to two vectors or vector fields X, Y as arguments. In the former case the output is a number, the (pseudo-)inner product of X and Y. In the latter case, the inner product of X_p, Y_p is taken at all points p on the manifold so that g(X, Y) defines a smooth function on M. Vector fields act (by definition) as differential operators on smooth functions. In local coordinates [math]\displaystyle{ (x_1,\ldots, x_n) }[/math], the action reads

[math]\displaystyle{ X(f) = X^i\frac{\partial}{\partial x^i}f = X^i\partial_i f }[/math]

where Einstein's summation convention is used.

Formal definition

An affine connection [math]\displaystyle{ \nabla }[/math] is called a Levi-Civita connection if

1. it preserves the metric, i.e., [math]\displaystyle{ \nabla g = 0 }[/math].
2. it is torsion-free, i.e., for any vector fields [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] we have [math]\displaystyle{ \nabla_X Y - \nabla_Y X = [X,Y] }[/math], where [math]\displaystyle{ [X, Y] }[/math] is the Lie bracket of the vector fields [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math].

Condition 1 above is sometimes referred to as compatibility with the metric, and condition 2 is sometimes called symmetry, cf. Do Carmo's text.

Fundamental theorem of (pseudo) Riemannian Geometry

Theorem Every pseudo Riemannian manifold [math]\displaystyle{ (M,g) }[/math] has a unique Levi Civita connection [math]\displaystyle{ \nabla }[/math].

proof: If a Levi-Civita connection exists, it must be unique. To see this, unravel the definition of the action of a connection on tensors to find

[math]\displaystyle{ X\bigl(g(Y,Z)\bigr) = (\nabla_X g)(Y, Z) + g(\nabla_X Y, Z) + g( Y, \nabla_X Z). }[/math]

Hence we can write condition 1 as

[math]\displaystyle{ X\bigl(g(Y,Z)\bigr) = g(\nabla_X Y, Z) + g( Y, \nabla_X Z). }[/math]

By the symmetry of the metric tensor [math]\displaystyle{ g }[/math] we then find:

[math]\displaystyle{ X \bigl(g(Y,Z)\bigr) + Y \bigl(g(Z,X)\bigr) - Z \bigl(g(Y,X)\bigr) = g(\nabla_X Y + \nabla_Y X, Z) + g(\nabla_X Z - \nabla_Z X, Y) + g(\nabla_Y Z - \nabla_Z Y, X). }[/math]

By condition 2, the right hand side is therefore equal to

[math]\displaystyle{ 2g(\nabla_X Y, Z) - g([X,Y], Z) + g([X,Z], Y) + g([Y,Z], X), }[/math]

and we find the Koszul formula

[math]\displaystyle{ g(\nabla_X Y, Z) = \tfrac{1}{2} \Big\{ X \bigl(g(Y,Z)\bigr) + Y \bigl(g(Z,X)\bigr) - Z \bigl(g(X,Y)\bigr) + g([X,Y],Z) - g([Y,Z], X) - g([X,Z], Y) \Big\}. }[/math]

Hence, if a Levi-Civita connection exists, it must be unique, because [math]\displaystyle{ Z }[/math] is arbitrary, [math]\displaystyle{ g }[/math] is non degenerate, and the right hand side does not depend on [math]\displaystyle{ \nabla }[/math].

To prove existence, note that for given vector field [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math], the right hand side of the Koszul expression is function-linear in the vector field [math]\displaystyle{ Z }[/math], not just real linear. Hence by the non degeneracy of [math]\displaystyle{ g }[/math], the right hand side uniquely defines some new vector field which we suggestively denote [math]\displaystyle{ \nabla_X Y }[/math] as in the left hand side. By substituting the Koszul formula, one now checks that for all vector fields [math]\displaystyle{ X, Y,Z }[/math], and all functions [math]\displaystyle{ f }[/math]

[math]\displaystyle{ g(\nabla_X (Y_1 + Y_2), Z) = g(\nabla_X Y_1, Z) + g(\nabla_X Y_2 , Z) }[/math]

[math]\displaystyle{ g(\nabla_X (f Y), Z) = X(f) g(Y, Z) + f g(\nabla_X Y,Z) }[/math]

[math]\displaystyle{ g(\nabla_X Y, Z) + g(\nabla_X Z, Y) = X\bigl(g(Y,Z)\bigr) }[/math]

[math]\displaystyle{ g(\nabla_X Y, Z) - g(\nabla_Y X, Z) = g([X,Y], Z). }[/math]

Hence the Koszul expression does, in fact, define a connection, and this connection is compatible with the metric and is torsion free, i.e. is a (hence the) Levi-Civita connection.

Note that with minor variations the same proof shows that there is a unique connection that is compatible with the metric and has prescribed torsion.

Christoffel symbols

Let [math]\displaystyle{ \nabla }[/math] be an affine connection on the tangent bundle. Choose local coordinates [math]\displaystyle{ x^1, \ldots, x^n }[/math] with coordinate basis vector fields [math]\displaystyle{ \partial_1, \ldots, \partial_n }[/math] and write [math]\displaystyle{ \nabla_j }[/math] for [math]\displaystyle{ \nabla_{\partial_j} }[/math]. The Christoffel symbols [math]\displaystyle{ \Gamma^l_{jk} }[/math] of [math]\displaystyle{ \nabla }[/math] with respect to these coordinates are defined as

[math]\displaystyle{ \nabla_j\partial_k = \Gamma^l_{jk} \partial_l }[/math]

The Christoffel symbols conversely define the connection [math]\displaystyle{ \nabla }[/math] on the coordinate neighbourhood because

[math]\displaystyle{ \begin{align} \nabla_X Y &= \nabla_{X^j\partial_j} (Y^k \partial_k) \\&= X^j\nabla_j(Y^k\partial_k) \\ &= X^j\bigl(\partial_j(Y^k)\partial_k + Y^k\nabla_j\partial_k\bigr) \\ &= X^j\bigl(\partial_j(Y^k)\partial_k + Y^k\Gamma^l_{jk}\partial_l\bigr) \\ &= X^j\bigl(\partial_j(Y^l) + Y^k\Gamma^l_{jk}\bigr)\partial_l \end{align} }[/math]

that is,

[math]\displaystyle{ (\nabla_j Y)^l = \partial_jY^l + \Gamma^l_{jk} Y^k }[/math]

An affine connection [math]\displaystyle{ \nabla }[/math] is compatible with a metric iff

[math]\displaystyle{ \partial_i \bigl(g(\partial_j, \partial_k) \bigr) = g(\nabla_i\partial_j, \partial_k) + g(\partial_j, \nabla_i\partial_k) = g(\Gamma^l_{ij}\partial_l, \partial_k) + g(\partial_j, \Gamma_{ik}^l\partial_l) }[/math]

i.e., if and only if

[math]\displaystyle{ \partial_i g_{jk} = \Gamma^l_{ij}g_{lk} + \Gamma^l_{ik}g_{jl}. }[/math]

An affine connection ∇ is torsion free iff

[math]\displaystyle{ \nabla_j\partial_k - \nabla_k \partial_j = (\Gamma^l_{jk} - \Gamma^l_{kj})\partial_l = [\partial_j, \partial_k]= 0. }[/math]

i.e., if and only if

[math]\displaystyle{ \Gamma^l_{jk} = \Gamma^l_{kj} }[/math]

is symmetric in its lower two indices.

As one checks by taking for [math]\displaystyle{ X, Y, Z }[/math], coordinate vector fields [math]\displaystyle{ \partial_j, \partial_k, \partial_l }[/math] (or computes directly), the Koszul expression of the Levi-Civita connection derived above is equivalent to a definition of the Christoffel symbols in terms of the metric as

[math]\displaystyle{ \Gamma^l_{jk} = \tfrac{1}{2} g^{lr} \left( \partial _k g_{rj} + \partial _j g_{rk} - \partial _r g_{jk} \right) }[/math]

where as usual [math]\displaystyle{ g^{ij} }[/math] are the coefficients of the dual metric tensor, i.e. the entries of the inverse of the matrix [math]\displaystyle{ g_{kl} }[/math].

Derivative along curve

The Levi-Civita connection (like any affine connection) also defines a derivative along curves, sometimes denoted by D.

Given a smooth curve γ on (M, g) and a vector field V along γ its derivative is defined by

[math]\displaystyle{ D_tV=\nabla_{\dot\gamma(t)}V. }[/math]

Formally, D is the pullback connection γ*∇ on the pullback bundle γ*TM.

In particular, [math]\displaystyle{ \dot\gamma(t) }[/math] is a vector field along the curve γ itself. If [math]\displaystyle{ \nabla_{\dot{\gamma}(t)}\dot{\gamma}(t) }[/math] vanishes, the curve is called a geodesic of the covariant derivative. Formally, the condition can be restated as the vanishing of the pullback connection applied to [math]\displaystyle{ \dot\gamma }[/math]:

[math]\displaystyle{ \left(\gamma^*\nabla\right) \dot{\gamma}\equiv 0. }[/math]

If the covariant derivative is the Levi-Civita connection of a certain metric, then the geodesics for the connection are precisely those geodesics of the metric that are parametrised proportionally to their arc length.

Parallel transport

In general, parallel transport along a curve with respect to a connection defines isomorphisms between the tangent spaces at the points of the curve. If the connection is a Levi-Civita connection, then these isomorphisms are orthogonal – that is, they preserve the inner products on the various tangent spaces.

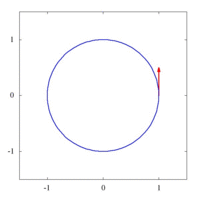
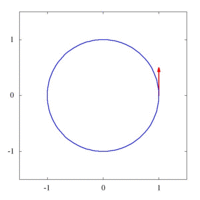
The images below show parallel transport of the Levi-Civita connection associated to two different Riemannian metrics on the plane, expressed in polar coordinates. The metric of left image corresponds to the standard Euclidean metric [math]\displaystyle{ ds^2 = dx^2 + dy^2 = dr^2 + r^2 d\theta^2 }[/math], while the metric on the right has standard form in polar coordinates (when [math]\displaystyle{ r = 1 }[/math]), and thus preserves the vector [math]\displaystyle{ {\partial \over \partial \theta} }[/math] tangent to the circle. This second metric has a singularity at the origin, as can be seen by expressing it in Cartesian coordinates:

[math]\displaystyle{ dr = \frac{xdx + ydy}{\sqrt{x^2 + y^2}} }[/math]

[math]\displaystyle{ d\theta = \frac{xdy - ydx}{x^2 + y^2} }[/math]

[math]\displaystyle{ dr^2 + d\theta^2 = \frac{(xdx + ydy)^2}{x^2+y^2} + \frac{(xdy - ydx)^2}{(x^2+y^2)^2} }[/math]

Parallel transports under Levi-Civita connections

This transport is given by the metric [math]\displaystyle{ ds^2 = dr^2 + r^2 d\theta^2 }[/math].

This transport is given by the metric [math]\displaystyle{ ds^2 = dr^2 + d\theta^2 }[/math].

Example: the unit sphere in R³

Let ⟨ , ⟩ be the usual scalar product on R³. Let S² be the unit sphere in R³. The tangent space to S² at a point m is naturally identified with the vector subspace of R³ consisting of all vectors orthogonal to m. It follows that a vector field Y on S² can be seen as a map Y : S² → R³, which satisfies [math]\displaystyle{ \bigl\langle Y(m), m\bigr\rangle = 0, \qquad \forall m\in \mathbf{S}^2. }[/math]

Denote as d_mY the differential of the map Y at the point m. Then we have:

Lemma — The formula [math]\displaystyle{ \left(\nabla_X Y\right)(m) = d_mY(X(m)) + \langle X(m),Y(m)\rangle m }[/math] defines an affine connection on S² with vanishing torsion.

Proof

It is straightforward to prove that ∇ satisfies the Leibniz identity and is C^∞(S²) linear in the first variable. It is also a straightforward computation to show that this connection is torsion free. So all that needs to be proved here is that the formula above produces a vector field tangent to S². That is, we need to prove that for all m in S² [math]\displaystyle{ \bigl\langle\left(\nabla_X Y\right)(m),m\bigr\rangle = 0\qquad (1). }[/math] Consider the map f that sends every m in S² to ⟨Y(m), m⟩, which is always 0. The map f is constant, hence its differential vanishes. In particular [math]\displaystyle{ d_mf(X) = \bigl\langle d_m Y(X),m\bigr\rangle + \bigl\langle Y(m), X(m)\bigr\rangle = 0. }[/math] The equation (1) above follows. Q.E.D.

In fact, this connection is the Levi-Civita connection for the metric on S² inherited from R³. Indeed, one can check that this connection preserves the metric.

Behavior under conformal rescaling

If the metric [math]\displaystyle{ g }[/math] in a conformal class is replaced by the conformally rescaled metric of the same class [math]\displaystyle{ \hat g=e^{2\gamma}g }[/math], then the Levi-Civita connection transforms according to the rule [math]\displaystyle{ \widehat\nabla_X Y = \nabla_XY + X(\gamma)Y + Y(\gamma)X - g(X,Y)\mathrm{grad}_g(\gamma). }[/math] where [math]\displaystyle{ \mathrm{grad}_g(\gamma) }[/math] is the gradient vector field of [math]\displaystyle{ \gamma }[/math] i.e. the vector field [math]\displaystyle{ g }[/math]-dual to [math]\displaystyle{ d\gamma }[/math], in local coordinates given by [math]\displaystyle{ g^{ik}(\partial_i \gamma)\partial_k }[/math]. Indeed, it is trivial to verify that [math]\displaystyle{ \widehat\nabla }[/math] is torsion-free. To verify metricity, assume that [math]\displaystyle{ g(Y,Y) }[/math] is constant. In that case, [math]\displaystyle{ \hat g(\widehat\nabla_XY,Y) = X(\gamma)\hat g(Y,Y) = \frac12 X(\hat g(Y,Y)). }[/math]

As an application, consider again the unit sphere, but this time under stereographic projection, so that the metric (in complex Fubini–Study coordinates [math]\displaystyle{ z,\bar z }[/math]) is: [math]\displaystyle{ g = \frac{4\,dz\,d\bar z}{(1+z\bar z)^2}. }[/math] This exhibits the metric of the sphere as conformally flat, with the Euclidean metric [math]\displaystyle{ dz\,d\bar z }[/math], with [math]\displaystyle{ \gamma = \ln(2)-\ln (1+z\bar z) }[/math]. We have [math]\displaystyle{ d\gamma = -(1+z\bar z)^{-1}(\bar z\, dz + z\,d{\bar z}) }[/math], and so [math]\displaystyle{ \widehat\nabla_{\partial_z}\partial_z = -\frac{2\bar z\partial_z}{1+z\bar z}. }[/math] With the Euclidean gradient [math]\displaystyle{ \mathrm{grad}_{Euc}(\gamma) = -(1+z\bar z)^{-1}(\bar z\partial_z + z\partial_{\bar z}) }[/math], we have [math]\displaystyle{ \widehat\nabla_{\partial_z}\partial_{\bar z} = 0. }[/math] These relations, together with their complex conjugates, define the Christoffel symbols for the two-sphere.

See also

• Weitzenböck connection

References

• Boothby, William M. (1986). An introduction to differentiable manifolds and Riemannian geometry. Academic Press. ISBN 0-12-116052-1. https://archive.org/details/introductiontodi0000boot. 
• Kobayashi, Shoshichi; Nomizu, Katsumi (1963). Foundations of differential geometry. John Wiley & Sons. ISBN 0-470-49647-9.  See Volume I pag. 158

External links

• Hazewinkel, Michiel, ed. (2001), "Levi-Civita connection", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4, https://www.encyclopediaofmath.org/index.php?title=p/l058230 
• MathWorld: Levi-Civita Connection
• PlanetMath: Levi-Civita Connection
• Levi-Civita connection at the Manifold Atlas