138 (number)
| ||||
|---|---|---|---|---|
| Cardinal | one hundred thirty-eight | |||
| Ordinal | 138th (one hundred thirty-eighth) | |||
| Factorization | 2 × 3 × 23 | |||
| Divisors | 1, 2, 3, 6, 23, 46, 69, 138 | |||
| Greek numeral | ΡΛΗ´ | |||
| Roman numeral | CXXXVIII | |||
| Binary | 100010102 | |||
| Ternary | 120103 | |||
| Quaternary | 20224 | |||
| Quinary | 10235 | |||
| Senary | 3506 | |||
| Octal | 2128 | |||
| Duodecimal | B612 | |||
| Hexadecimal | 8A16 | |||
| Vigesimal | 6I20 | |||
| Base 36 | 3U36 | |||
138 (one hundred [and] thirty-eight) is the natural number following 137 and preceding 139.
In mathematics
138 is a sphenic number,[1] and the smallest product of three primes such that in base 10, the third prime is a concatenation of the other two: [math]\displaystyle{ 2 \cdot 3 \cdot 23 }[/math].[lower-alpha 1] It is also a one-step palindrome in decimal (138 + 831 = 969).
138 has eight total divisors that generate an arithmetic mean of 36,[2] which is the eighth triangular number.[3] While the sum of the digits of 138 is 12, the product of its digits is 24.[4]
138 is an Ulam number,[5] the thirty-first abundant number,[6] and a primitive (square-free) congruent number.[7] It is the third 47-gonal number.[8]
As an interprime, 138 lies between the eleventh pair of twin primes (137, 139),[9] respectively the 33rd and 34th prime numbers.[10]
It is the sum of two consecutive primes (67 + 71),[11] and the sum of four consecutive primes (29 + 31 + 37 + 41).[12]
There are a total of 44 numbers that are relatively prime with 138 (and up to),[13] while 22 is its reduced totient.[14]
138 is the denominator of the twenty-second Bernoulli number [math]\displaystyle{ B_{n} }[/math] (whose respective numerator, is 854513).[15][16]
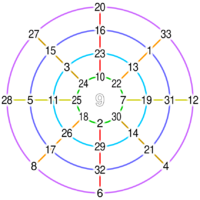
A magic sum of 138 is generated inside four magic circles that features the first thirty-three non-zero integers, with a 9 in the center (first constructed by Yang Hui).[lower-alpha 2]
The simplest Catalan solid, the triakis tetrahedron, produces 138 stellations (depending on rules chosen),[lower-alpha 3] 44 of which are fully symmetric and 94 of which are enantiomorphs.[17]
Using two radii to divide a circle according to the golden ratio yields sectors of approximately 138 degrees (the golden angle), and 222 degrees.
In science
- The Saros number of the solar eclipse series which began on June 6, 1472, and will end on July 11, 2716. The duration of Saros series 138 is 1244 years, and it contains 70 solar eclipses
- 138 Tolosa is a brightly colored, stony main belt asteroid
- The New General Catalogue object NGC 138, a spiral galaxy in the constellation Pisces
- 138P/Shoemaker-Levy is a periodic comet in the Solar System
In media
- "We Are 138", a 1978 song by the American punk rock band Misfits.
- Who's Afraid of 138!? is a trance record label operated by Dutch DJ Armin van Buuren, as a reference to the use of 138 BPM in some forms of trance music.[18][19]
See also
- The year AD 138 or 138 BC
- List of highways numbered 138
Notes
- ↑ The only other number less than 1000 in decimal with this property is 777 = 3 × 7 × 37.
- ↑ This magic sum is generated from points that simultaneously lie on circles and diagonals, and, importantly, without including 9 in this sum (i.e. by bypassing it).
- ↑ Using a different set of rules than Miller's rules for stellating polyhedra. For example, by Miller's rules, the triakis tetrahedron produces a total of 188 stellations, 136 of which are chiral. Using this same set of (Miller) rules, its dual polyhedron, the truncated tetrahedron, produces only 9 stellations, without including the truncated tetrahedron.
References
- ↑ Sloane, N. J. A., ed. "Sequence A007304 (Sphenic numbers: products of 3 distinct primes.)". OEIS Foundation. https://oeis.org/A007304. Retrieved 2023-07-24.
- ↑ Sloane, N. J. A., ed. "Sequence A003601 (Numbers n such that the average of the divisors of n is an integer)". OEIS Foundation. https://oeis.org/A003601. Retrieved 2023-07-24.
- ↑ Sloane, N. J. A., ed. "Sequence A000217 (Triangular numbers)". OEIS Foundation. https://oeis.org/A000217. Retrieved 2023-07-24.
- ↑ "138". https://www.numbersaplenty.com/138.
- ↑ Sloane, N. J. A., ed. "Sequence A002858 (Ulam numbers)". OEIS Foundation. https://oeis.org/A002858. Retrieved 2023-07-24.
- ↑ Sloane, N. J. A., ed. "Sequence A005101 (Abundant numbers (sum of divisors of m exceeds 2m).)". OEIS Foundation. https://oeis.org/A005101. Retrieved 2023-07-24.
- ↑ Sloane, N. J. A., ed. "Sequence A006991 (Primitive congruent numbers.)". OEIS Foundation. https://oeis.org/A006991. Retrieved 2023-07-24.
- ↑ Sloane, N. J. A., ed. "Sequence A095311 (47-gonal numbers)". OEIS Foundation. https://oeis.org/A095311. Retrieved 2016-05-27.
- ↑ Sloane, N. J. A., ed. "Sequence A014574 (Average of twin prime pairs.)". OEIS Foundation. https://oeis.org/A014574. Retrieved 2023-07-24.
- ↑ Sloane, N. J. A., ed. "Sequence A006093 (a(n) equal to prime(n) - 1.)". OEIS Foundation. https://oeis.org/A006093. Retrieved 2023-07-24.
- ↑ Sloane, N. J. A., ed. "Sequence A001097 (Twin primes.)". OEIS Foundation. https://oeis.org/A001097. Retrieved 2023-07-24.
- ↑ Sloane, N. J. A., ed. "Sequence A034963 (Sums of four consecutive primes.)". OEIS Foundation. https://oeis.org/A034963.
- ↑ Sloane, N. J. A., ed. "Sequence A000010 (Euler totient function phi(n): count numbers less than or equal to n and prime to n.)". OEIS Foundation. https://oeis.org/A000010. Retrieved 2023-07-24.
- ↑ Sloane, N. J. A., ed. "Sequence A002322 (Reduced totient function psi(n))". OEIS Foundation. https://oeis.org/A002322. Retrieved 2023-07-24.
- ↑ Sloane, N. J. A., ed. "Sequence A027642 (Denominator of Bernoulli number B_n.)". OEIS Foundation. https://oeis.org/A027642. Retrieved 2023-07-24.
- ↑ Sloane, N. J. A., ed. "Sequence A027641 (Numerator of Bernoulli number B_n.)". OEIS Foundation. https://oeis.org/A027641. Retrieved 2023-07-24.
- ↑ Wenninger, Magnus J. (1983). "Chapter 3: Stellated forms of convex duals". Dual Models. Cambridge, UK: Cambridge University Press. pp. 36-37. doi:10.1017/CBO9780511569371. ISBN 9780521245241. OCLC 8785984. https://www.cambridge.org/core/books/dual-models/7F1B1D1AEF65D83BB77F516AEBA22919.
- ↑ "Who’s Afraid Of 138?!". https://www.armadamusic.com/labels/whos-afraid-of-138.
- ↑ "Who's Afraid Of 138?!". https://www.beatport.com/label/whos-afraid-of-138/33972.
 |

