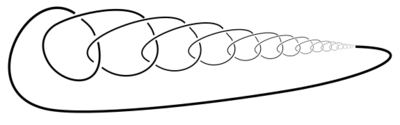
Wild knot
In the mathematical theory of knots, a knot is tame if it can be "thickened", that is, if there exists an extension to an embedding of the solid torus [math]\displaystyle{ S^1\times D^2 }[/math] into the 3-sphere. A knot is tame if and only if it can be represented as a finite closed polygonal chain. Every closed curve containing a wild arc is a wild knot.[1] Knots that are not tame are called wild and can have pathological behavior. In knot theory and 3-manifold theory, often the adjective "tame" is omitted. Smooth knots, for example, are always tame.
It has been conjectured that every wild knot has infinitely many quadrisecants.[2]
As well as their mathematical study, wild knots have also been studied for their decorative purposes in Celtic-style ornamental knotwork.[3]
See also
- Eilenberg–Mazur swindle, a technique for analyzing connected sums using infinite sums of knots
References
- ↑ Hazewinkel, Michiel, ed. (2001), "Wild knot", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4, https://www.encyclopediaofmath.org/index.php?title=Main_Page
- ↑ "Quadrisecants of knots and links", Journal of Knot Theory and Its Ramifications 3: 41–50, 1994, doi:10.1142/S021821659400006X
- ↑ Browne, Cameron (December 2006), "Wild knots", Computers & Graphics 30 (6): 1027–1032, doi:10.1016/j.cag.2006.08.021
 |