Unit sphere
In mathematics, a unit sphere is a sphere of unit radius: the set of points at Euclidean distance 1 from some center point in three-dimensional space. More generally, the unit [math]\displaystyle{ n }[/math]-sphere is an [math]\displaystyle{ n }[/math]-sphere of unit radius in [math]\displaystyle{ (n+1) }[/math]-dimensional Euclidean space; the unit circle is a special case, the unit [math]\displaystyle{ 1 }[/math]-sphere in the plane. An (open) unit ball is the region inside of a unit sphere, the set of points of distance less than 1 from the center.
A sphere or ball with unit radius and center at the origin of the space is called the unit sphere or the unit ball. Any arbitrary sphere can be transformed to the unit sphere by a combination of translation and scaling, so the study of spheres in general can often be reduced to the study of the unit sphere.
The unit sphere is often used as a model for spherical geometry because it has constant sectional curvature of 1, which simplifies calculations. In trigonometry, circular arc length on the unit circle is called radians and used for measuring angular distance; in spherical trigonometry surface area on the unit sphere is called steradians and used for measuring solid angle.
In more general contexts, a unit sphere is the set of points of distance 1 from a fixed central point, where different norms can be used as general notions of "distance", and an (open) unit ball is the region inside.
Unit spheres and balls in Euclidean space
In Euclidean space of [math]\displaystyle{ n }[/math] dimensions, the [math]\displaystyle{ (n-1) }[/math]-dimensional unit sphere is the set of all points [math]\displaystyle{ (x_1, \ldots, x_n) }[/math] which satisfy the equation
- [math]\displaystyle{ x_1^2 + x_2^2 + \cdots + x_n ^2 = 1. }[/math]
The open unit [math]\displaystyle{ n }[/math]-ball is the set of all points satisfying the inequality
- [math]\displaystyle{ x_1^2 + x_2^2 + \cdots + x_n ^2 \lt 1, }[/math]
and closed unit [math]\displaystyle{ n }[/math]-ball is the set of all points satisfying the inequality
- [math]\displaystyle{ x_1^2 + x_2^2 + \cdots + x_n ^2 \le 1. }[/math]
Volume and area
The classical equation of a unit sphere is that of the ellipsoid with a radius of 1 and no alterations to the [math]\displaystyle{ x }[/math]-, [math]\displaystyle{ y }[/math]-, or [math]\displaystyle{ z }[/math]- axes:
- [math]\displaystyle{ x^2 + y^2 + z^2 = 1 }[/math]
The volume of the unit ball in Euclidean [math]\displaystyle{ n }[/math]-space, and the surface area of the unit sphere, appear in many important formulas of analysis. The volume of the unit [math]\displaystyle{ n }[/math]-ball, which we denote [math]\displaystyle{ V_n, }[/math] can be expressed by making use of the gamma function. It is
- [math]\displaystyle{ V_n = \frac{\pi ^ {n/2}}{\Gamma(1+n/2)} = \begin{cases} {\pi^{n/2}}/{(n/2)!} & \mathrm{if~}n \ge 0\mathrm{~is~even} \\[6mu] {2(2\pi)^{(n-1)/2}}/{n!!} & \mathrm{if~}n \ge 0\mathrm{~is~odd,} \end{cases} }[/math]
where [math]\displaystyle{ n!! }[/math] is the double factorial.
The hypervolume of the [math]\displaystyle{ (n-1) }[/math]-dimensional unit sphere (i.e., the "area" of the boundary of the [math]\displaystyle{ n }[/math]-dimensional unit ball), which we denote [math]\displaystyle{ A_{n-1}, }[/math] can be expressed as
- [math]\displaystyle{ A_{n-1} = n V_n = \frac{n \pi ^ {n/2}}{\Gamma(1+n/2)} = \frac{2 \pi ^ {n/2}}{\Gamma(n/2)} = \begin{cases} {2 \pi^{n/2}}/{(n/2 - 1)!} & \mathrm{if~}n \ge 1\mathrm{~is~even} \\[6mu] {2(2\pi)^{(n-1)/2}}/{(n-2)!!} & \mathrm{if~}n \ge 1\mathrm{~is~odd.} \end{cases} }[/math]
For example, [math]\displaystyle{ A_0 = 2 }[/math] is the "area" of the boundary of the unit ball [math]\displaystyle{ [-1,1] \subset \mathbb{R} }[/math], which simply counts the two points. Then [math]\displaystyle{ A_1 = 2\pi }[/math] is the "area" of the boundary of the unit disc, which is the circumference of the unit circle. [math]\displaystyle{ A_2 = 4\pi }[/math] is the area of the boundary of the unit ball [math]\displaystyle{ \{ x \in \R^3 : x_1^2 + x_2^2 + x_3^2 \leq 1 \} }[/math], which is the surface area of the unit sphere [math]\displaystyle{ \{ x \in \R^3 : x_1^2 + x_2^2 + x_3^2 = 1 \} }[/math].
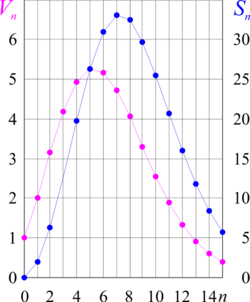
The surface areas and the volumes for some values of [math]\displaystyle{ n }[/math] are as follows:
| [math]\displaystyle{ n }[/math] | [math]\displaystyle{ A_{n-1} }[/math] (surface area) | [math]\displaystyle{ V_n }[/math] (volume) | ||
|---|---|---|---|---|
| 0 | [math]\displaystyle{ (1/0!)\pi^0 }[/math] | 1 | ||
| 1 | [math]\displaystyle{ 1(2^1/1!!)\pi^0 }[/math] | 2 | [math]\displaystyle{ (2^1/1!!)\pi^0 }[/math] | 2 |
| 2 | [math]\displaystyle{ 2(1/1!)\pi^1 = 2 \pi }[/math] | 6.283 | [math]\displaystyle{ (1/1!)\pi^1 = \pi }[/math] | 3.141 |
| 3 | [math]\displaystyle{ 3(2^2/3!!)\pi^1 = 4 \pi }[/math] | 12.57 | [math]\displaystyle{ (2^2/3!!)\pi^1 = (4/3)\pi }[/math] | 4.189 |
| 4 | [math]\displaystyle{ 4(1/2!)\pi^2 = 2 \pi^2 }[/math] | 19.74 | [math]\displaystyle{ (1/2!)\pi^2 = (1/2)\pi^2 }[/math] | 4.935 |
| 5 | [math]\displaystyle{ 5(2^3/5!!)\pi^2 = (8/3)\pi^2 }[/math] | 26.32 | [math]\displaystyle{ (2^3/5!!)\pi^2 = (8/15)\pi^2 }[/math] | 5.264 |
| 6 | [math]\displaystyle{ 6(1/3!)\pi^3 = \pi^3 }[/math] | 31.01 | [math]\displaystyle{ (1/3!)\pi^3 = (1/6)\pi^3 }[/math] | 5.168 |
| 7 | [math]\displaystyle{ 7(2^4/7!!) \pi^3 = (16/15)\pi^3 }[/math] | 33.07 | [math]\displaystyle{ (2^4/7!!) \pi^3 = (16/105)\pi^3 }[/math] | 4.725 |
| 8 | [math]\displaystyle{ 8(1/4!)\pi^4 = (1/3)\pi^4 }[/math] | 32.47 | [math]\displaystyle{ (1/4!)\pi^4 = (1/24)\pi^4 }[/math] | 4.059 |
| 9 | [math]\displaystyle{ 9(2^5/9!!) \pi^4 = (32/105)\pi^4 }[/math] | 29.69 | [math]\displaystyle{ (2^5/9!!) \pi^4 = (32/945)\pi^4 }[/math] | 3.299 |
| 10 | [math]\displaystyle{ 10(1/5!)\pi^5 = (1/12)\pi^5 }[/math] | 25.50 | [math]\displaystyle{ (1/5!)\pi^5 = (1/120)\pi^5 }[/math] | 2.550 |
where the decimal expanded values for [math]\displaystyle{ n \geq 2 }[/math] are rounded to the displayed precision.
Recursion
The [math]\displaystyle{ A_n }[/math] values satisfy the recursion:
- [math]\displaystyle{ A_0 = 2 }[/math]
- [math]\displaystyle{ A_1 = 2\pi }[/math]
- [math]\displaystyle{ A_n = \frac{2 \pi}{n-1} A_{n-2} }[/math] for [math]\displaystyle{ n \gt 1 }[/math].
The [math]\displaystyle{ V_n }[/math] values satisfy the recursion:
- [math]\displaystyle{ V_0 = 1 }[/math]
- [math]\displaystyle{ V_1 = 2 }[/math]
- [math]\displaystyle{ V_n = \frac{2 \pi}{n} V_{n-2} }[/math] for [math]\displaystyle{ n \gt 1 }[/math].
Non-negative real-valued dimensions
The value [math]\displaystyle{ 2^{-n} V_n = \pi ^ {n/2} \big/\, 2^n \Gamma\bigl(1+\tfrac12n\bigr) }[/math] at non-negative real values of [math]\displaystyle{ n }[/math] is sometimes used for normalization of Hausdorff measure.[1][2]
Other radii
The surface area of an [math]\displaystyle{ (n-1) }[/math]-sphere with radius [math]\displaystyle{ r }[/math] is [math]\displaystyle{ A_{n-1} r^{n-1} }[/math] and the volume of an [math]\displaystyle{ n }[/math]- ball with radius [math]\displaystyle{ r }[/math] is [math]\displaystyle{ V_{n} r^{n}. }[/math] For instance, the area is [math]\displaystyle{ A_2 = 4\pi r^2 }[/math] for the two-dimensional surface of the three-dimensional ball of radius [math]\displaystyle{ r. }[/math] The volume is [math]\displaystyle{ V_3 = \tfrac43\pi r^3 }[/math] for the three-dimensional ball of radius [math]\displaystyle{ r }[/math].
Unit balls in normed vector spaces
The open unit ball of a normed vector space [math]\displaystyle{ V }[/math] with the norm [math]\displaystyle{ \|\cdot\| }[/math] is given by
- [math]\displaystyle{ \{ x\in V: \|x\|\lt 1 \} }[/math]
It is the topological interior of the closed unit ball of [math]\displaystyle{ (V, \|\cdot\|)\colon }[/math]
- [math]\displaystyle{ \{ x\in V: \|x\|\le 1\} }[/math]
The latter is the disjoint union of the former and their common border, the unit sphere of [math]\displaystyle{ (V, \|\cdot\|)\colon }[/math]
- [math]\displaystyle{ \{ x\in V: \|x\| = 1 \} }[/math]
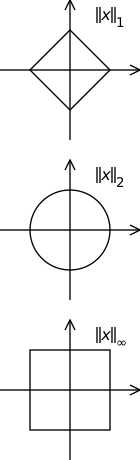
The "shape" of the unit ball is entirely dependent on the chosen norm; it may well have "corners", and for example may look like [math]\displaystyle{ [-1,1]^n }[/math] in the case of the max-norm in [math]\displaystyle{ \mathbb{R}^n }[/math]. One obtains a naturally round ball as the unit ball pertaining to the usual Hilbert space norm, based in the finite-dimensional case on the Euclidean distance; its boundary is what is usually meant by the unit sphere.
Let [math]\displaystyle{ x=(x_1,...x_n)\in \R^n. }[/math] Define the usual [math]\displaystyle{ \ell_p }[/math]-norm for [math]\displaystyle{ p \ge 1 }[/math] as:
- [math]\displaystyle{ \|x\|_p = \biggl(\sum_{k=1}^n |x_k|^p \biggr)^{1/p} }[/math]
Then [math]\displaystyle{ \|x\|_2 }[/math] is the usual Hilbert space norm. [math]\displaystyle{ \|x\|_1 }[/math] is called the Hamming norm, or [math]\displaystyle{ \ell_1 }[/math]-norm. The condition [math]\displaystyle{ p \geq 1 }[/math] is necessary in the definition of the [math]\displaystyle{ \ell_p }[/math] norm, as the unit ball in any normed space must be convex as a consequence of the triangle inequality. Let [math]\displaystyle{ \|x\|_\infty }[/math] denote the max-norm or [math]\displaystyle{ \ell_\infty }[/math]-norm of [math]\displaystyle{ x }[/math].
Note that for the one-dimensional circumferences [math]\displaystyle{ C_p }[/math] of the two-dimensional unit balls, we have:
- [math]\displaystyle{ C_{1} = 4 \sqrt{2} }[/math] is the minimum value.
- [math]\displaystyle{ C_{2} = 2 \pi }[/math]
- [math]\displaystyle{ C_{\infty} = 8 }[/math] is the maximum value.
Generalizations
Metric spaces
All three of the above definitions can be straightforwardly generalized to a metric space, with respect to a chosen origin. However, topological considerations (interior, closure, border) need not apply in the same way (e.g., in ultrametric spaces, all of the three are simultaneously open and closed sets), and the unit sphere may even be empty in some metric spaces.
Quadratic forms
If [math]\displaystyle{ V }[/math] is a linear space with a real quadratic form [math]\displaystyle{ F : V \to \R, }[/math] then [math]\displaystyle{ \{ p \in V : F(p) = 1\} }[/math] may be called the unit sphere[3][4] or unit quasi-sphere of [math]\displaystyle{ V. }[/math] For example, the quadratic form [math]\displaystyle{ x^2 - y^2 }[/math], when set equal to one, produces the unit hyperbola, which plays the role of the "unit circle" in the plane of split-complex numbers. Similarly, the quadratic form [math]\displaystyle{ x^2 }[/math] yields a pair of lines for the unit sphere in the dual number plane.
See also
- Ball
- [math]\displaystyle{ n }[/math]-sphere
- Sphere
- Superellipse
- Unit circle
- Unit disk
- Unit tangent bundle
- Unit square
Notes and references
- ↑ The Chinese University of Hong Kong, Math 5011, Chapter 3, Lebesgue and Hausdorff Measures
- ↑ Manin, Yuri I.. "The notion of dimension in geometry and algebra". Bulletin of the American Mathematical Society 43 (2): 139–161. https://www.ams.org/bull/2006-43-02/S0273-0979-06-01081-0/S0273-0979-06-01081-0.pdf. Retrieved 17 December 2021.
- ↑ Takashi Ono (1994) Variations on a Theme of Euler: quadratic forms, elliptic curves, and Hopf maps, chapter 5: Quadratic spherical maps, page 165, Plenum Press, ISBN 0-306-44789-4
- ↑ F. Reese Harvey (1990) Spinors and calibrations, "Generalized Spheres", page 42, Academic Press, ISBN 0-12-329650-1
- Mahlon M. Day (1958) Normed Linear Spaces, page 24, Springer-Verlag.
- Deza, E.; Deza, M. (2006), Dictionary of Distances, Elsevier, ISBN 0-444-52087-2. Reviewed in Newsletter of the European Mathematical Society 64 (June 2007), p. 57. This book is organized as a list of distances of many types, each with a brief description.
External links
es:1-esfera
 |