6-demicubic honeycomb

6-demicubic honeycomb
(No image)
Type	Uniform 6-honeycomb
Family	Alternated hypercube honeycomb
Schläfli symbol	h{4,3,3,3,3,4} h{4,3,3,3,31,1} ht0,6{4,3,3,3,3,4}
Coxeter diagram	= =
Facets	{3,3,3,3,4} h{4,3,3,3,3}
Vertex figure	r{3,3,3,3,4}
Coxeter group	[math]\displaystyle{ {\tilde{B}}_6 }[/math] [4,3,3,3,31,1] [math]\displaystyle{ {\tilde{D}}_6 }[/math] [31,1,3,3,31,1]

The 6-demicubic honeycomb or demihexeractic honeycomb is a uniform space-filling tessellation (or honeycomb) in Euclidean 6-space. It is constructed as an alternation of the regular 6-cube honeycomb.

It is composed of two different types of facets. The 6-cubes become alternated into 6-demicubes h{4,3,3,3,3} and the alternated vertices create 6-orthoplex {3,3,3,3,4} facets.

D6 lattice

The vertex arrangement of the 6-demicubic honeycomb is the D₆ lattice. The 60 vertices of the rectified 6-orthoplex vertex figure of the 6-demicubic honeycomb reflect the kissing number 60 of this lattice. The best known is 72, from the E₆ lattice and the 2₂₂ honeycomb.

The D+6 lattice (also called D26) can be constructed by the union of two D₆ lattices. This packing is only a lattice for even dimensions. The kissing number is 2⁵=32 (2^n-1 for n<8, 240 for n=8, and 2n(n-1) for n>8).

∪

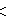
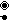
The D*6 lattice (also called D46 and C26) can be constructed by the union of all four 6-demicubic lattices: It is also the 6-dimensional body centered cubic, the union of two 6-cube honeycombs in dual positions.

∪ ∪ ∪ = ∪ .

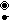
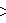
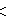
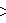
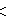
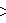
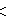
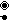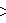
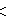
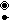
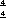
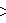
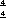
The kissing number of the D₆^* lattice is 12 (2n for n≥5). and its Voronoi tessellation is a trirectified 6-cubic honeycomb, , containing all birectified 6-orthoplex Voronoi cell, .

Symmetry constructions

There are three uniform construction symmetries of this tessellation. Each symmetry can be represented by arrangements of different colors on the 64 6-demicube facets around each vertex.

Coxeter group	Schläfli symbol	Coxeter-Dynkin diagram	Vertex figure Symmetry	Facets/verf
[math]\displaystyle{ {\tilde{B}}_6 }[/math] = [31,1,3,3,3,4] = [1+,4,3,3,3,3,4]	h{4,3,3,3,3,4}	=	[3,3,3,4]	64: 6-demicube 12: 6-orthoplex
[math]\displaystyle{ {\tilde{D}}_6 }[/math] = [31,1,3,31,1] = [1+,4,3,3,31,1]	h{4,3,3,3,31,1}	=	[33,1,1]	32+32: 6-demicube 12: 6-orthoplex
½[math]\displaystyle{ {\tilde{C}}_6 }[/math] = (4,3,3,3,4,2+)	ht0,6{4,3,3,3,3,4}			32+16+16: 6-demicube 12: 6-orthoplex

See also

• 6-cubic honeycomb

External links

• Kaleidoscopes: Selected Writings of H. S. M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN:978-0-471-01003-6 [2]
  • (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
• Conway JH, Sloane NJH (1998). Sphere Packings, Lattices and Groups (3rd ed.). ISBN 0-387-98585-9. https://archive.org/details/spherepackingsla0000conw_b8u0. 

Fundamental convex regular and uniform honeycombs in dimensions 2-9
Space	Family	[math]\displaystyle{ {\tilde{A}}_{n-1} }[/math]	[math]\displaystyle{ {\tilde{C}}_{n-1} }[/math]	[math]\displaystyle{ {\tilde{B}}_{n-1} }[/math]	[math]\displaystyle{ {\tilde{D}}_{n-1} }[/math]	[math]\displaystyle{ {\tilde{G}}_2 }[/math] / [math]\displaystyle{ {\tilde{F}}_4 }[/math] / [math]\displaystyle{ {\tilde{E}}_{n-1} }[/math]
E2	Uniform tiling	{3[3]}	δ3	hδ3	qδ3	Hexagonal
E3	Uniform convex honeycomb	{3[4]}	δ4	hδ4	qδ4
E4	Uniform 4-honeycomb	{3[5]}	δ5	hδ5	qδ5	24-cell honeycomb
E5	Uniform 5-honeycomb	{3[6]}	δ6	hδ6	qδ6
E6	Uniform 6-honeycomb	{3[7]}	δ7	hδ7	qδ7	222
E7	Uniform 7-honeycomb	{3[8]}	δ8	hδ8	qδ8	133 • 331
E8	Uniform 8-honeycomb	{3[9]}	δ9	hδ9	qδ9	152 • 251 • 521
E9	Uniform 9-honeycomb	{3[10]}	δ10	hδ10	qδ10
En-1	Uniform (n-1)-honeycomb	{3[n]}	δn	hδn	qδn	1k2 • 2k1 • k21