8-simplex honeycomb

8-simplex honeycomb
(No image)
Type	Uniform 8-honeycomb
Family	Simplectic honeycomb
Schläfli symbol	{3[9]}
Coxeter diagram
6-face types	{37} , t1{37} 30px t2{37} 30px, t3{37}
6-face types	{36} , t1{36} 30px t2{36} 40px, t3{36}
6-face types	{35} , t1{35} 30px t2{35}
5-face types	{34} , t1{34} 30px t2{34}
4-face types	{33} , t1{33}
Cell types	{3,3} , t1{3,3}
Face types	{3}
Vertex figure	t0,7{37}
Symmetry	[math]\displaystyle{ {\tilde{A}}_8 }[/math]×2, 3[9]
Properties	vertex-transitive

In eighth-dimensional Euclidean geometry, the 8-simplex honeycomb is a space-filling tessellation (or honeycomb). The tessellation fills space by 8-simplex, rectified 8-simplex, birectified 8-simplex, and trirectified 8-simplex facets. These facet types occur in proportions of 1:1:1:1 respectively in the whole honeycomb.

A8 lattice

This vertex arrangement is called the A8 lattice or 8-simplex lattice. The 72 vertices of the expanded 8-simplex vertex figure represent the 72 roots of the [math]\displaystyle{ {\tilde{A}}_8 }[/math] Coxeter group. It is the 8-dimensional case of a simplectic honeycomb. Around each vertex figure are 510 facets: 9+9 8-simplex, 36+36 rectified 8-simplex, 84+84 birectified 8-simplex, 126+126 trirectified 8-simplex, with the count distribution from the 10th row of Pascal's triangle.

[math]\displaystyle{ {\tilde{E}}_8 }[/math] contains [math]\displaystyle{ {\tilde{A}}_8 }[/math] as a subgroup of index 5760. Both [math]\displaystyle{ {\tilde{E}}_8 }[/math] and [math]\displaystyle{ {\tilde{A}}_8 }[/math] can be seen as affine extensions of [math]\displaystyle{ A_8 }[/math] from different nodes:

The A38 lattice is the union of three A₈ lattices, and also identical to the E8 lattice.

∪ ∪ = .

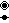
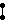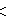
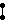The A*8 lattice (also called A98) is the union of nine A₈ lattices, and has the vertex arrangement of the dual honeycomb to the omnitruncated 8-simplex honeycomb, and therefore the Voronoi cell of this lattice is an omnitruncated 8-simplex

∪ ∪ ∪ ∪ ∪ ∪ ∪ ∪ = dual of .

Related polytopes and honeycombs

This honeycomb is one of 45 unique uniform honeycombs constructed by the [math]\displaystyle{ {\tilde{A}}_8 }[/math] Coxeter group. The symmetry can be multiplied by the ring symmetry of the Coxeter diagrams:

A8 honeycombs
Enneagon symmetry	Symmetry	Extended diagram	Extended group	Honeycombs
a1	[3[9]]		[math]\displaystyle{ {\tilde{A}}_8 }[/math]
i2	[[3[9]]]		[math]\displaystyle{ {\tilde{A}}_8 }[/math]×2	1 2
i6	[3[3[9]]]		[math]\displaystyle{ {\tilde{A}}_8 }[/math]×6
r18	[9[3[9]]]		[math]\displaystyle{ {\tilde{A}}_8 }[/math]×18	3

Projection by folding

The 8-simplex honeycomb can be projected into the 4-dimensional tesseractic honeycomb by a geometric folding operation that maps two pairs of mirrors into each other, sharing the same vertex arrangement:

[math]\displaystyle{ {\tilde{A}}_8 }[/math]
[math]\displaystyle{ {\tilde{C}}_4 }[/math]

See also

• Regular and uniform honeycombs in 8-space:
  • 8-cubic honeycomb
  • 8-demicubic honeycomb
  • Truncated 8-simplex honeycomb
  • 5₂₁ honeycomb
  • 2₅₁ honeycomb
  • 1₅₂ honeycomb

References

• Norman Johnson Uniform Polytopes, Manuscript (1991)
• Kaleidoscopes: Selected Writings of H. S. M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN:978-0-471-01003-6 [1]
  • (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380–407, MR 2,10] (1.9 Uniform space-fillings)
  • (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3–45]

Fundamental convex regular and uniform honeycombs in dimensions 2-9
Space	Family	[math]\displaystyle{ {\tilde{A}}_{n-1} }[/math]	[math]\displaystyle{ {\tilde{C}}_{n-1} }[/math]	[math]\displaystyle{ {\tilde{B}}_{n-1} }[/math]	[math]\displaystyle{ {\tilde{D}}_{n-1} }[/math]	[math]\displaystyle{ {\tilde{G}}_2 }[/math] / [math]\displaystyle{ {\tilde{F}}_4 }[/math] / [math]\displaystyle{ {\tilde{E}}_{n-1} }[/math]
E2	Uniform tiling	{3[3]}	δ3	hδ3	qδ3	Hexagonal
E3	Uniform convex honeycomb	{3[4]}	δ4	hδ4	qδ4
E4	Uniform 4-honeycomb	{3[5]}	δ5	hδ5	qδ5	24-cell honeycomb
E5	Uniform 5-honeycomb	{3[6]}	δ6	hδ6	qδ6
E6	Uniform 6-honeycomb	{3[7]}	δ7	hδ7	qδ7	222
E7	Uniform 7-honeycomb	{3[8]}	δ8	hδ8	qδ8	133 • 331
E8	Uniform 8-honeycomb	{3[9]}	δ9	hδ9	qδ9	152 • 251 • 521
E9	Uniform 9-honeycomb	{3[10]}	δ10	hδ10	qδ10
En-1	Uniform (n-1)-honeycomb	{3[n]}	δn	hδn	qδn	1k2 • 2k1 • k21