Simplectic honeycomb
| [math]\displaystyle{ {\tilde{A}}_2 }[/math] | [math]\displaystyle{ {\tilde{A}}_3 }[/math] |
|---|---|
| Triangular tiling | Tetrahedral-octahedral honeycomb |
 With red and yellow equilateral triangles |
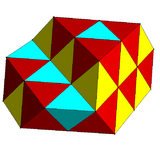 With cyan and yellow tetrahedra, and red rectified tetrahedra (octahedra) |
  
|
  
|
In geometry, the simplectic honeycomb (or n-simplex honeycomb) is a dimensional infinite series of honeycombs, based on the [math]\displaystyle{ {\tilde{A}}_n }[/math] affine Coxeter group symmetry. It is represented by a Coxeter-Dynkin diagram as a cyclic graph of n + 1 nodes with one node ringed. It is composed of n-simplex facets, along with all rectified n-simplices. It can be thought of as an n-dimensional hypercubic honeycomb that has been subdivided along all hyperplanes [math]\displaystyle{ x+y+\cdots\in\mathbb{Z} }[/math], then stretched along its main diagonal until the simplices on the ends of the hypercubes become regular. The vertex figure of an n-simplex honeycomb is an expanded n-simplex.
In 2 dimensions, the honeycomb represents the triangular tiling, with Coxeter graph filling the plane with alternately colored triangles. In 3 dimensions it represents the tetrahedral-octahedral honeycomb, with Coxeter graph filling space with alternately tetrahedral and octahedral cells. In 4 dimensions it is called the 5-cell honeycomb, with Coxeter graph 
, with 5-cell and rectified 5-cell facets. In 5 dimensions it is called the 5-simplex honeycomb, with Coxeter graph , filling space by 5-simplex, rectified 5-simplex, and birectified 5-simplex facets. In 6 dimensions it is called the 6-simplex honeycomb, with Coxeter graph , filling space by 6-simplex, rectified 6-simplex, and birectified 6-simplex facets.
By dimension
| n | [math]\displaystyle{ {\tilde{A}}_{2+} }[/math] | Tessellation | Vertex figure | Facets per vertex figure | Vertices per vertex figure | Edge figure |
|---|---|---|---|---|---|---|
| 1 | [math]\displaystyle{ {\tilde{A}}_1 }[/math] |  Apeirogon 
|
Line segment
|
2 | 2 | Point |
| 2 | [math]\displaystyle{ {\tilde{A}}_2 }[/math] | Triangular tiling 2-simplex honeycomb
|
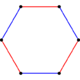 Hexagon (Truncated triangle) 
|
3+3 triangles | 6 | Line segment |
| 3 | [math]\displaystyle{ {\tilde{A}}_3 }[/math] | Tetrahedral-octahedral honeycomb 3-simplex honeycomb
|
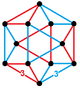 Cuboctahedron (Cantellated tetrahedron)
|
4+4 tetrahedron 6 rectified tetrahedra |
12 |  Rectangle |
| 4 | [math]\displaystyle{ {\tilde{A}}_4 }[/math] | 4-simplex honeycomb
|
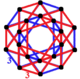 Runcinated 5-cell
|
5+5 5-cells 10+10 rectified 5-cells |
20 |  Triangular antiprism |
| 5 | [math]\displaystyle{ {\tilde{A}}_5 }[/math] | 5-simplex honeycomb
|
 Stericated 5-simplex
|
6+6 5-simplex 15+15 rectified 5-simplex 20 birectified 5-simplex |
30 |  Tetrahedral antiprism |
| 6 | [math]\displaystyle{ {\tilde{A}}_6 }[/math] | 6-simplex honeycomb
|
 Pentellated 6-simplex
|
7+7 6-simplex 21+21 rectified 6-simplex 35+35 birectified 6-simplex |
42 | 4-simplex antiprism |
| 7 | [math]\displaystyle{ {\tilde{A}}_7 }[/math] | 7-simplex honeycomb
|
 Hexicated 7-simplex
|
8+8 7-simplex 28+28 rectified 7-simplex 56+56 birectified 7-simplex 70 trirectified 7-simplex |
56 | 5-simplex antiprism |
| 8 | [math]\displaystyle{ {\tilde{A}}_8 }[/math] | 8-simplex honeycomb
|
 Heptellated 8-simplex
|
9+9 8-simplex 36+36 rectified 8-simplex 84+84 birectified 8-simplex 126+126 trirectified 8-simplex |
72 | 6-simplex antiprism |
| 9 | [math]\displaystyle{ {\tilde{A}}_9 }[/math] | 9-simplex honeycomb
|
 Octellated 9-simplex
|
10+10 9-simplex 45+45 rectified 9-simplex 120+120 birectified 9-simplex 210+210 trirectified 9-simplex 252 quadrirectified 9-simplex |
90 | 7-simplex antiprism |
| 10 | [math]\displaystyle{ {\tilde{A}}_{10} }[/math] | 10-simplex honeycomb
|
 Ennecated 10-simplex
|
11+11 10-simplex 55+55 rectified 10-simplex 165+165 birectified 10-simplex 330+330 trirectified 10-simplex 462+462 quadrirectified 10-simplex |
110 | 8-simplex antiprism |
| 11 | [math]\displaystyle{ {\tilde{A}}_{11} }[/math] | 11-simplex honeycomb | ... | ... | ... | ... |
Projection by folding
The (2n-1)-simplex honeycombs and 2n-simplex honeycombs can be projected into the n-dimensional hypercubic honeycomb by a geometric folding operation that maps two pairs of mirrors into each other, sharing the same vertex arrangement:
| [math]\displaystyle{ {\tilde{A}}_2 }[/math] |
|
[math]\displaystyle{ {\tilde{A}}_4 }[/math] |
|
[math]\displaystyle{ {\tilde{A}}_6 }[/math] |
|
[math]\displaystyle{ {\tilde{A}}_8 }[/math] |
|
[math]\displaystyle{ {\tilde{A}}_{10} }[/math] |
|
... |
|---|---|---|---|---|---|---|---|---|---|---|
| [math]\displaystyle{ {\tilde{A}}_3 }[/math] |  
|
[math]\displaystyle{ {\tilde{A}}_3 }[/math] |
|
[math]\displaystyle{ {\tilde{A}}_5 }[/math] |
|
[math]\displaystyle{ {\tilde{A}}_7 }[/math] |
|
[math]\displaystyle{ {\tilde{A}}_9 }[/math] |
|
... |
| [math]\displaystyle{ {\tilde{C}}_1 }[/math] |
|
[math]\displaystyle{ {\tilde{C}}_2 }[/math] | 
|
[math]\displaystyle{ {\tilde{C}}_3 }[/math] |
|
[math]\displaystyle{ {\tilde{C}}_4 }[/math] |
|
[math]\displaystyle{ {\tilde{C}}_5 }[/math] |
|
... |
Kissing number
These honeycombs, seen as tangent n-spheres located at the center of each honeycomb vertex have a fixed number of contacting spheres and correspond to the number of vertices in the vertex figure. This represents the highest kissing number for 2 and 3 dimensions, but falls short on higher dimensions. In 2-dimensions, the triangular tiling defines a circle packing of 6 tangent spheres arranged in a regular hexagon, and for 3 dimensions there are 12 tangent spheres arranged in a cuboctahedral configuration. For 4 to 8 dimensions, the kissing numbers are 20, 30, 42, 56, and 72 spheres, while the greatest solutions are 24, 40, 72, 126, and 240 spheres respectively.
See also
- Hypercubic honeycomb
- Alternated hypercubic honeycomb
- Quarter hypercubic honeycomb
- Truncated simplectic honeycomb
- Omnitruncated simplectic honeycomb
References
- George Olshevsky, Uniform Panoploid Tetracombs, Manuscript (2006) (Complete list of 11 convex uniform tilings, 28 convex uniform honeycombs, and 143 convex uniform tetracombs)
- Branko Grünbaum, Uniform tilings of 3-space. Geombinatorics 4(1994), 49 - 56.
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- Coxeter, H.S.M. Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8
- Kaleidoscopes: Selected Writings of H. S. M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10] (1.9 Uniform space-fillings)
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
Fundamental convex regular and uniform honeycombs in dimensions 2-9
| ||||||
|---|---|---|---|---|---|---|
| Space | Family | [math]\displaystyle{ {\tilde{A}}_{n-1} }[/math] | [math]\displaystyle{ {\tilde{C}}_{n-1} }[/math] | [math]\displaystyle{ {\tilde{B}}_{n-1} }[/math] | [math]\displaystyle{ {\tilde{D}}_{n-1} }[/math] | [math]\displaystyle{ {\tilde{G}}_2 }[/math] / [math]\displaystyle{ {\tilde{F}}_4 }[/math] / [math]\displaystyle{ {\tilde{E}}_{n-1} }[/math] |
| E2 | Uniform tiling | {3[3]} | δ3 | hδ3 | qδ3 | Hexagonal |
| E3 | Uniform convex honeycomb | {3[4]} | δ4 | hδ4 | qδ4 | |
| E4 | Uniform 4-honeycomb | {3[5]} | δ5 | hδ5 | qδ5 | 24-cell honeycomb |
| E5 | Uniform 5-honeycomb | {3[6]} | δ6 | hδ6 | qδ6 | |
| E6 | Uniform 6-honeycomb | {3[7]} | δ7 | hδ7 | qδ7 | 222 |
| E7 | Uniform 7-honeycomb | {3[8]} | δ8 | hδ8 | qδ8 | 133 • 331 |
| E8 | Uniform 8-honeycomb | {3[9]} | δ9 | hδ9 | qδ9 | 152 • 251 • 521 |
| E9 | Uniform 9-honeycomb | {3[10]} | δ10 | hδ10 | qδ10 | |
| En-1 | Uniform (n-1)-honeycomb | {3[n]} | δn | hδn | qδn | 1k2 • 2k1 • k21 |
 |
