Quarter 5-cubic honeycomb

quarter 5-cubic honeycomb
(No image)
Type	Uniform 5-honeycomb
Family	Quarter hypercubic honeycomb
Schläfli symbol	q{4,3,3,3,4}
Coxeter-Dynkin diagram	=
5-face type	h{4,33}, h4{4,33},
Vertex figure	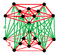Rectified 5-cell antiprism or Stretched birectified 5-simplex
Coxeter group	[math]\displaystyle{ {\tilde{D}}_5 }[/math]×2 = 31,1,3,31,1
Dual
Properties	vertex-transitive

In five-dimensional Euclidean geometry, the quarter 5-cubic honeycomb is a uniform space-filling tessellation (or honeycomb). It has half the vertices of the 5-demicubic honeycomb, and a quarter of the vertices of a 5-cube honeycomb. Its facets are 5-demicubes and runcinated 5-demicubes.

See also

Regular and uniform honeycombs in 5-space:

• 5-cube honeycomb
• 5-demicube honeycomb
• 5-simplex honeycomb
• Truncated 5-simplex honeycomb
• Omnitruncated 5-simplex honeycomb

References

• Kaleidoscopes: Selected Writings of H. S. M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
  • (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45] See p318 [2]
• Klitzing, Richard. "5D Euclidean tesselations#5D". https://bendwavy.org/klitzing/dimensions/flat.htm.  x3o3o x3o3o *b3*e - spaquinoh

Fundamental convex regular and uniform honeycombs in dimensions 2-9
Space	Family	[math]\displaystyle{ {\tilde{A}}_{n-1} }[/math]	[math]\displaystyle{ {\tilde{C}}_{n-1} }[/math]	[math]\displaystyle{ {\tilde{B}}_{n-1} }[/math]	[math]\displaystyle{ {\tilde{D}}_{n-1} }[/math]	[math]\displaystyle{ {\tilde{G}}_2 }[/math] / [math]\displaystyle{ {\tilde{F}}_4 }[/math] / [math]\displaystyle{ {\tilde{E}}_{n-1} }[/math]
E2	Uniform tiling	{3[3]}	δ3	hδ3	qδ3	Hexagonal
E3	Uniform convex honeycomb	{3[4]}	δ4	hδ4	qδ4
E4	Uniform 4-honeycomb	{3[5]}	δ5	hδ5	qδ5	24-cell honeycomb
E5	Uniform 5-honeycomb	{3[6]}	δ6	hδ6	qδ6
E6	Uniform 6-honeycomb	{3[7]}	δ7	hδ7	qδ7	222
E7	Uniform 7-honeycomb	{3[8]}	δ8	hδ8	qδ8	133 • 331
E8	Uniform 8-honeycomb	{3[9]}	δ9	hδ9	qδ9	152 • 251 • 521
E9	Uniform 9-honeycomb	{3[10]}	δ10	hδ10	qδ10
En-1	Uniform (n-1)-honeycomb	{3[n]}	δn	hδn	qδn	1k2 • 2k1 • k21