Astronomy:Cosmic distance ladder
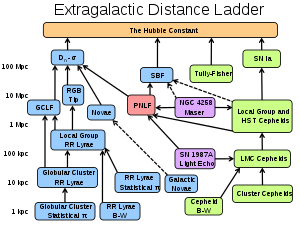
- Light green boxes: Technique applicable to star-forming galaxies.
- Light blue boxes: Technique applicable to population II galaxies.
- Light Purple boxes: Geometric distance technique.
- Light Red box: The planetary nebula luminosity function technique is applicable to all populations of the Virgo Supercluster.
- Solid black lines: Well calibrated ladder step.
- Dashed black lines: Uncertain calibration ladder step.
The cosmic distance ladder (also known as the extragalactic distance scale) is the succession of methods by which astronomers determine the distances to celestial objects. A direct distance measurement of an astronomical object is possible only for those objects that are "close enough" (within about a thousand parsecs) to Earth. The techniques for determining distances to more distant objects are all based on various measured correlations between methods that work at close distances and methods that work at larger distances. Several methods rely on a standard candle, which is an astronomical object that has a known luminosity.
The ladder analogy arises because no single technique can measure distances at all ranges encountered in astronomy. Instead, one method can be used to measure nearby distances, a second can be used to measure nearby to intermediate distances, and so on. Each rung of the ladder provides information that can be used to determine the distances at the next higher rung.
Direct measurement

At the base of the ladder are fundamental distance measurements, in which distances are determined directly, with no physical assumptions about the nature of the object in question. The precise measurement of stellar positions is part of the discipline of astrometry. Early fundamental distances—such as the radii of the earth, moon and sun, and the distances between them—were well estimated with very low technology by the ancient Greeks.[2]
Astronomical unit
Direct distance measurements are based upon the astronomical unit (AU), which is defined as the mean distance between the Earth and the Sun. Kepler's laws provide precise ratios of the sizes of the orbits of objects orbiting the Sun, but provide no measurement of the overall scale of the orbit system. Radar is used to measure the distance between the orbits of the Earth and of a second body. From that measurement and the ratio of the two orbit sizes, the size of Earth's orbit is calculated. The Earth's orbit is known with an absolute precision of a few meters and a relative precision of a few parts in 100 billion (1×10−11).
Historically, observations of Venus transits were crucial in determining the AU; in the first half of the 20th century, observations of asteroids were also important. Presently the orbit of Earth is determined with high precision using radar measurements of distances to Venus and other nearby planets and asteroids,[3] and by tracking interplanetary spacecraft in their orbits around the Sun through the Solar System.
Parallax
Standard candles
Almost all astronomical objects used as physical distance indicators belong to a class that has a known brightness. By comparing this known luminosity to an object's observed brightness, the distance to the object can be computed using the inverse-square law. These objects of known brightness are termed standard candles, coined by Henrietta Swan Leavitt.[4]
The brightness of an object can be expressed in terms of its absolute magnitude. This quantity is derived from the logarithm of its luminosity as seen from a distance of 10 parsecs. The apparent magnitude, the magnitude as seen by the observer (an instrument called a bolometer is used), can be measured and used with the absolute magnitude to calculate the distance d to the object in parsecs[5] as follows: [math]\displaystyle{ 5 \cdot \log_{10} d = m - M + 5 }[/math] or [math]\displaystyle{ d = 10^{(m - M + 5)/5} }[/math] where m is the apparent magnitude, and M the absolute magnitude. For this to be accurate, both magnitudes must be in the same frequency band and there can be no relative motion in the radial direction. Some means of correcting for interstellar extinction, which also makes objects appear fainter and more red, is needed, especially if the object lies within a dusty or gaseous region.[6] The difference between an object's absolute and apparent magnitudes is called its distance modulus, and astronomical distances, especially intergalactic ones, are sometimes tabulated in this way.
Problems
Two problems exist for any class of standard candle. The principal one is calibration, that is the determination of exactly what the absolute magnitude of the candle is. This includes defining the class well enough that members can be recognized, and finding enough members of that class with well-known distances to allow their true absolute magnitude to be determined with enough accuracy. The second problem lies in recognizing members of the class, and not mistakenly using a standard candle calibration on an object which does not belong to the class. At extreme distances, which is where one most wishes to use a distance indicator, this recognition problem can be quite serious.
A significant issue with standard candles is the recurring question of how standard they are. For example, all observations seem to indicate that Type Ia supernovae that are of known distance have the same brightness (corrected by the shape of the light curve). The basis for this closeness in brightness is discussed below; however, the possibility exists that the distant Type Ia supernovae have different properties than nearby Type Ia supernovae. The use of Type Ia supernovae is crucial in determining the correct cosmological model. If indeed the properties of Type Ia supernovae are different at large distances, i.e. if the extrapolation of their calibration to arbitrary distances is not valid, ignoring this variation can dangerously bias the reconstruction of the cosmological parameters, in particular the reconstruction of the matter density parameter.Cite error: Closing </ref> missing for <ref> tag[7]:38
[math]\displaystyle{ \frac{df}{dt} = \frac{96\pi^{8/3}(G\mathcal M)^\frac 53 f^\frac{11}3}{5\,c^5}, }[/math]
where [math]\displaystyle{ G }[/math] is the gravitational constant, [math]\displaystyle{ c }[/math] is the speed of light, and [math]\displaystyle{ \mathcal{M} }[/math] is a single (therefore computable[lower-alpha 1]) number called the chirp mass of the system, a combination of the masses [math]\displaystyle{ (m_1,m_2) }[/math] of the two objects[9]
[math]\displaystyle{ \mathcal{M} = \frac{(m_1m_2)^{3/5}}{(m_1+m_2)^{1/5}}. }[/math]
By observing the waveform, the chirp mass can be computed and thence the power (rate of energy emission) of the gravitational waves. Thus, such a gravitational wave source is a standard siren of known loudness.[10][7]
Just as with standard candles, given the emitted and received amplitudes, the inverse-square law determines the distance to the source. There are some differences with standard candles, however. Gravitational waves are not emitted isotropically, but measuring the polarisation of the wave provides enough information to determine the angle of emission. Gravitational wave detectors also have anisotropic antenna patterns, so the position of the source on the sky relative to the detectors is needed to determine the angle of reception. Generally, if a wave is detected by a network of three detectors at different locations, the network will measure enough information to make these corrections and obtain the distance. Also unlike standard candles, gravitational waves need no calibration against other distance measures. The measurement of distance does of course require the calibration of the gravitational wave detectors, but then the distance is fundamentally given as a multiple of the wavelength of the laser light being used in the gravitational wave interferometer.
There are other considerations that limit the accuracy of this distance, besides detector calibration. Fortunately, gravitational waves are not subject to extinction due to an intervening absorbing medium. But they are subject to gravitational lensing, in the same way as light. If a signal is strongly lensed, then it might be received as multiple events, separated in time (the analogue of multiple images of a quasar, for example). Less easy to discern and control for is the effect of weak lensing, where the signal's path through space is affected by many small magnification and demagnification events. This will be important for signals originating at cosmological redshifts greater than 1. Finally, it is difficult for detector networks to measure the polarization of a signal accurately if the binary system is observed nearly face-on;[11] such signals suffer significantly larger errors in the distance measurement. Unfortunately, binaries radiate most strongly perpendicular to the orbital plane, so face-on signals are intrinsically stronger and the most commonly observed.
If the binary consists of a pair of neutron stars, their merger will be accompanied by a kilonova/hypernova explosion that may allow the position to be accurately identified by electromagnetic telescopes. In such cases, the redshift of the host galaxy allows a determination of the Hubble constant [math]\displaystyle{ H_0 }[/math].[9] This was the case for GW170817, which was used to make the first such measurement.[12] Even if no electromagnetic counterpart can be identified for an ensemble of signals, it is possible to use a statistical method to infer the value of [math]\displaystyle{ H_0 }[/math].[9]
Standard ruler
Another class of physical distance indicator is the standard ruler. In 2008, galaxy diameters have been proposed as a possible standard ruler for cosmological parameter determination.[13] More recently the physical scale imprinted by baryon acoustic oscillations (BAO) in the early universe has been used. In the early universe (before recombination) the baryons and photons scatter off each other, and form a tightly coupled fluid that can support sound waves. The waves are sourced by primordial density perturbations, and travel at speed that can be predicted from the baryon density and other cosmological parameters. The total distance that these sound waves can travel before recombination determines a fixed scale, which simply expands with the universe after recombination. BAO therefore provide a standard ruler that can be measured in galaxy surveys from the effect of baryons on the clustering of galaxies. The method requires an extensive galaxy survey in order to make this scale visible, but has been measured with percent-level precision (see baryon acoustic oscillations). The scale does depend on cosmological parameters like the baryon and matter densities, and the number of neutrinos, so distances based on BAO are more dependent on cosmological model than those based on local measurements.
Light echos can be also used as standard rulers,[14][15] although it is challenging to correctly measure the source geometry.[16][17]
Galactic distance indicators
With few exceptions, distances based on direct measurements are available only out to about a thousand parsecs, which is a modest portion of our own Galaxy. For distances beyond that, measures depend upon physical assumptions, that is, the assertion that one recognizes the object in question, and the class of objects is homogeneous enough that its members can be used for meaningful estimation of distance.
Physical distance indicators, used on progressively larger distance scales, include:
- Dynamical parallax, uses orbital parameters of visual binaries to measure the mass of the system, and hence use the mass–luminosity relation to determine the luminosity
- Eclipsing binaries — In the last decade, measurement of eclipsing binaries' fundamental parameters has become possible with 8-meter class telescopes. This makes it feasible to use them as indicators of distance. Recently, they have been used to give direct distance estimates to the Large Magellanic Cloud (LMC), Small Magellanic Cloud (SMC), Andromeda Galaxy and Triangulum Galaxy. Eclipsing binaries offer a direct method to gauge the distance to galaxies to a new improved 5% level of accuracy which is feasible with current technology to a distance of around 3 Mpc (3 million parsecs).[18]
- RR Lyrae variables — used for measuring distances within the galaxy and in nearby globular clusters.
- The following four indicators all use stars in the old stellar populations (Population II):[19]
- Tip of the red-giant branch (TRGB) distance indicator.
- Planetary nebula luminosity function (PNLF)
- Globular cluster luminosity function (GCLF)
- Surface brightness fluctuation (SBF)
- In galactic astronomy, X-ray bursts (thermonuclear flashes on the surface of a neutron star) are used as standard candles. Observations of X-ray burst sometimes show X-ray spectra indicating radius expansion. Therefore, the X-ray flux at the peak of the burst should correspond to Eddington luminosity, which can be calculated once the mass of the neutron star is known (1.5 solar masses is a commonly used assumption). This method allows distance determination of some low-mass X-ray binaries. Low-mass X-ray binaries are very faint in the optical, making their distances extremely difficult to determine.
- Interstellar masers can be used to derive distances to galactic and some extragalactic objects that have maser emission.
- Cepheids and novae
- The Tully–Fisher relation
- The Faber–Jackson relation
- Type Ia supernovae that have a very well-determined maximum absolute magnitude as a function of the shape of their light curve and are useful in determining extragalactic distances up to a few hundred Mpc.[20] A notable exception is SN 2003fg, the "Champagne Supernova", a Type Ia supernova of unusual nature.
- Redshifts and Hubble's law
Main sequence fitting
When the absolute magnitude for a group of stars is plotted against the spectral classification of the star, in a Hertzsprung–Russell diagram, evolutionary patterns are found that relate to the mass, age and composition of the star. In particular, during their hydrogen burning period, stars lie along a curve in the diagram called the main sequence. By measuring these properties from a star's spectrum, the position of a main sequence star on the H–R diagram can be determined, and thereby the star's absolute magnitude estimated. A comparison of this value with the apparent magnitude allows the approximate distance to be determined, after correcting for interstellar extinction of the luminosity because of gas and dust.
In a gravitationally-bound star cluster such as the Hyades, the stars formed at approximately the same age and lie at the same distance. This allows relatively accurate main sequence fitting, providing both age and distance determination.
Extragalactic distance scale
| Method | Uncertainty for Single Galaxy (mag) | Distance to Virgo Cluster (Mpc) | Range (Mpc) |
|---|---|---|---|
| Classical Cepheids | 0.16 | 15–25 | 29 |
| Novae | 0.4 | 21.1 ± 3.9 | 20 |
| Planetary Nebula Luminosity Function | 0.3 | 15.4 ± 1.1 | 50 |
| Globular Cluster Luminosity Function | 0.4 | 18.8 ± 3.8 | 50 |
| Surface Brightness Fluctuations | 0.3 | 15.9 ± 0.9 | 50 |
| Sigma-D relation | 0.5 | 16.8 ± 2.4 | > 100 |
| Type Ia Supernovae | 0.10 | 19.4 ± 5.0 | > 1000 |
The extragalactic distance scale is a series of techniques used today by astronomers to determine the distance of cosmological bodies beyond our own galaxy, which are not easily obtained with traditional methods. Some procedures use properties of these objects, such as stars, globular clusters, nebulae, and galaxies as a whole. Other methods are based more on the statistics and probabilities of things such as entire galaxy clusters.
Wilson–Bappu effect
Discovered in 1956 by Olin Wilson and M.K. Vainu Bappu, the Wilson–Bappu effect uses the effect known as spectroscopic parallax. Many stars have features in their spectra, such as the calcium K-line, that indicate their absolute magnitude. The distance to the star can then be calculated from its apparent magnitude using the distance modulus.
There are major limitations to this method for finding stellar distances. The calibration of the spectral line strengths has limited accuracy and it requires a correction for interstellar extinction. Though in theory this method has the ability to provide reliable distance calculations to stars up to 7 megaparsecs (Mpc), it is generally only used for stars at hundreds of kiloparsecs (kpc).
Classical Cepheids
Beyond the reach of the Wilson–Bappu effect, the next method relies on the period-luminosity relation of classical Cepheid variable stars. The following relation can be used to calculate the distance to Galactic and extragalactic classical Cepheids:
Script error: No such module "in5".[math]\displaystyle{ 5\log_{10}{d}=V+ (3.34) \log_{10}{P} - (2.45) (V-I) + 7.52 \,. }[/math][22]
Script error: No such module "in5".[math]\displaystyle{ 5\log_{10}{d}=V+ (3.37) \log_{10}{P} - (2.55) (V-I) + 7.48 \,. }[/math][23]
Several problems complicate the use of Cepheids as standard candles and are actively debated, chief among them are: the nature and linearity of the period-luminosity relation in various passbands and the impact of metallicity on both the zero-point and slope of those relations, and the effects of photometric contamination (blending) and a changing (typically unknown) extinction law on Cepheid distances.[24][25][26][27][28][29][30][31][32]
These unresolved matters have resulted in cited values for the Hubble constant ranging between 60 km/s/Mpc and 80 km/s/Mpc. Resolving this discrepancy is one of the foremost problems in astronomy since some cosmological parameters of the Universe may be constrained significantly better by supplying a precise value of the Hubble constant.[33][34]
Cepheid variable stars were the key instrument in Edwin Hubble's 1923 conclusion that M31 (Andromeda) was an external galaxy, as opposed to a smaller nebula within the Milky Way. He was able to calculate the distance of M31 to 285 kpc, today's value being 770 kpc.[citation needed]
As detected thus far, NGC 3370, a spiral galaxy in the constellation Leo, contains the farthest Cepheids yet found at a distance of 29 Mpc. Cepheid variable stars are in no way perfect distance markers: at nearby galaxies they have an error of about 7% and up to a 15% error for the most distant.[citation needed]
Supernovae

There are several different methods for which supernovae can be used to measure extragalactic distances.
Measuring a supernova's photosphere
We can assume that a supernova expands in a spherically symmetric manner. If the supernova is close enough such that we can measure the angular extent, θ(t), of its photosphere, we can use the equation
[math]\displaystyle{ \omega = \frac{\Delta\theta}{\Delta t} \,, }[/math] where ω is angular velocity, θ is angular extent. In order to get an accurate measurement, it is necessary to make two observations separated by time Δt. Subsequently, we can use
[math]\displaystyle{ \ d = \frac{V_{ej}}{\omega} \,, }[/math] where d is the distance to the supernova, Vej is the supernova's ejecta's radial velocity (it can be assumed that Vej equals Vθ if spherically symmetric).
This method works only if the supernova is close enough to be able to measure accurately the photosphere. Similarly, the expanding shell of gas is in fact not perfectly spherical nor a perfect blackbody. Also interstellar extinction can hinder the accurate measurements of the photosphere. This problem is further exacerbated by core-collapse supernova. All of these factors contribute to the distance error of up to 25%.
Type Ia light curves
Type Ia supernovae are some of the best ways to determine extragalactic distances. Ia's occur when a binary white dwarf star begins to accrete matter from its companion star. As the white dwarf gains matter, eventually it reaches its Chandrasekhar limit of [math]\displaystyle{ 1.4 M_{\odot} }[/math].
Once reached, the star becomes unstable and undergoes a runaway nuclear fusion reaction. Because all Type Ia supernovae explode at about the same mass, their absolute magnitudes are all the same. This makes them very useful as standard candles. All Type Ia supernovae have a standard blue and visual magnitude of
[math]\displaystyle{ \ M_B \approx M_V \approx -19.3 \pm 0.3 \,. }[/math] Therefore, when observing a Type Ia supernova, if it is possible to determine what its peak magnitude was, then its distance can be calculated. It is not intrinsically necessary to capture the supernova directly at its peak magnitude; using the multicolor light curve shape method (MLCS), the shape of the light curve (taken at any reasonable time after the initial explosion) is compared to a family of parameterized curves that will determine the absolute magnitude at the maximum brightness. This method also takes into effect interstellar extinction/dimming from dust and gas.
Similarly, the stretch method fits the particular supernovae magnitude light curves to a template light curve. This template, as opposed to being several light curves at different wavelengths (MLCS) is just a single light curve that has been stretched (or compressed) in time. By using this Stretch Factor, the peak magnitude can be determined.[35]
Using Type Ia supernovae is one of the most accurate methods, particularly since supernova explosions can be visible at great distances (their luminosities rival that of the galaxy in which they are situated), much farther than Cepheid Variables (500 times farther). Much time has been devoted to the refining of this method. The current uncertainty approaches a mere 5%, corresponding to an uncertainty of just 0.1 magnitudes.
Novae in distance determinations
Novae can be used in much the same way as supernovae to derive extragalactic distances. There is a direct relation between a nova's max magnitude and the time for its visible light to decline by two magnitudes. This relation is shown to be:
[math]\displaystyle{ \ M^\max_V = -9.96 - 2.31 \log_{10} \dot{x} \,. }[/math] Where [math]\displaystyle{ \dot{x} }[/math] is the time derivative of the nova's mag, describing the average rate of decline over the first 2 magnitudes.
After novae fade, they are about as bright as the most luminous Cepheid variable stars, therefore both these techniques have about the same max distance: ~ 20 Mpc. The error in this method produces an uncertainty in magnitude of about ±0.4
Globular cluster luminosity function
Based on the method of comparing the luminosities of globular clusters (located in galactic halos) from distant galaxies to that of the Virgo Cluster, the globular cluster luminosity function carries an uncertainty of distance of about 20% (or 0.4 magnitudes).
US astronomer William Alvin Baum first attempted to use globular clusters to measure distant elliptical galaxies. He compared the brightest globular clusters in Virgo A galaxy with those in Andromeda, assuming the luminosities of the clusters were the same in both. Knowing the distance to Andromeda, Baum has assumed a direct correlation and estimated Virgo A's distance.
Baum used just a single globular cluster, but individual formations are often poor standard candles. Canadian astronomer René Racine assumed the use of the globular cluster luminosity function (GCLF) would lead to a better approximation. The number of globular clusters as a function of magnitude is given by:
[math]\displaystyle{ \ \Phi (m) = A e^{(m-m_0)^2/2\sigma^2} \, }[/math] where m0 is the turnover magnitude, M0 is the magnitude of the Virgo cluster, and sigma is the dispersion ~ 1.4 mag.
It is assumed that globular clusters all have roughly the same luminosities within the universe. There is no universal globular cluster luminosity function that applies to all galaxies.
Planetary nebula luminosity function
Like the GCLF method, a similar numerical analysis can be used for planetary nebulae within far off galaxies. The planetary nebula luminosity function (PNLF) was first proposed in the late 1970s by Holland Cole and David Jenner. They suggested that all planetary nebulae might all have similar maximum intrinsic brightness, now calculated to be M = −4.53. This would therefore make them potential standard candles for determining extragalactic distances.
Astronomer George Howard Jacoby and his colleagues later proposed that the PNLF function equaled:
[math]\displaystyle{ \ N (M) \propto e^{0.307 M} (1 - e^{3(M^{*} - M)} ) \,. }[/math] Where N(M) is number of planetary nebula, having absolute magnitude M. M* is equal to the nebula with the brightest magnitude.
Surface brightness fluctuation method
The following method deals with the overall inherent properties of galaxies. These methods, though with varying error percentages, have the ability to make distance estimates beyond 100 Mpc, though it is usually applied more locally.
The surface brightness fluctuation (SBF) method takes advantage of the use of CCD cameras on telescopes. Because of spatial fluctuations in a galaxy's surface brightness, some pixels on these cameras will pick up more stars than others. However, as distance increases the picture will become increasingly smoother. Analysis of this describes a magnitude of the pixel-to-pixel variation, which is directly related to a galaxy's distance.[36]
Sigma-D relation
The Sigma-D relation (or Σ-D relation), used in elliptical galaxies, relates the angular diameter (D) of the galaxy to its velocity dispersion. It is important to describe exactly what D represents, in order to understand this method. It is, more precisely, the galaxy's angular diameter out to the surface brightness level of 20.75 B-mag arcsec−2. This surface brightness is independent of the galaxy's actual distance from us. Instead, D is inversely proportional to the galaxy's distance, represented as d. Thus, this relation does not employ standard candles. Rather, D provides a standard ruler. This relation between D and Σ is
[math]\displaystyle{ \log (D) = 1.333 \log (\Sigma) + C }[/math] where C is a constant which depends on the distance to the galaxy clusters.[37]
This method has the potential to become one of the strongest methods of galactic distance calculators, perhaps exceeding the range of even the Tully–Fisher method. As of today, however, elliptical galaxies are not bright enough to provide a calibration for this method through the use of techniques such as Cepheids. Instead, calibration is done using more crude methods.
Overlap and scaling
A succession of distance indicators, which is the distance ladder, is needed for determining distances to other galaxies. The reason is that objects bright enough to be recognized and measured at such distances are so rare that few or none are present nearby, so there are too few examples close enough with reliable trigonometric parallax to calibrate the indicator. For example, Cepheid variables, one of the best indicators for nearby spiral galaxies, cannot yet be satisfactorily calibrated by parallax alone, though the Gaia space mission can now weigh in on that specific problem. The situation is further complicated by the fact that different stellar populations generally do not have all types of stars in them. Cepheids in particular are massive stars, with short lifetimes, so they will only be found in places where stars have very recently been formed. Consequently, because elliptical galaxies usually have long ceased to have large-scale star formation, they will not have Cepheids. Instead, distance indicators whose origins are in an older stellar population (like novae and RR Lyrae variables) must be used. However, RR Lyrae variables are less luminous than Cepheids, and novae are unpredictable and an intensive monitoring program—and luck during that program—is needed to gather enough novae in the target galaxy for a good distance estimate.
Because the more distant steps of the cosmic distance ladder depend upon the nearer ones, the more distant steps include the effects of errors in the nearer steps, both systematic and statistical ones. The result of these propagating errors means that distances in astronomy are rarely known to the same level of precision as measurements in the other sciences, and that the precision necessarily is poorer for more distant types of object.
Another concern, especially for the very brightest standard candles, is their "standardness": how homogeneous the objects are in their true absolute magnitude. For some of these different standard candles, the homogeneity is based on theories about the formation and evolution of stars and galaxies, and is thus also subject to uncertainties in those aspects. For the most luminous of distance indicators, the Type Ia supernovae, this homogeneity is known to be poor[38][clarification needed]; however, no other class of object is bright enough to be detected at such large distances, so the class is useful simply because there is no real alternative.
The observational result of Hubble's Law, the proportional relationship between distance and the speed with which a galaxy is moving away from us (usually referred to as redshift) is a product of the cosmic distance ladder. Edwin Hubble observed that fainter galaxies are more redshifted. Finding the value of the Hubble constant was the result of decades of work by many astronomers, both in amassing the measurements of galaxy redshifts and in calibrating the steps of the distance ladder. Hubble's Law is the primary means we have for estimating the distances of quasars and distant galaxies in which individual distance indicators cannot be seen.
See also
Footnotes
- ↑ If the signal were to depend on the individual masses separately, there would not be enough observable information in the signal at the lowest order to infer its intrinsic loudness. This degeneracy between the masses therefore is crucial for the loudness measurement, but it is no accident: It has a fundamental origin in the scale-free nature of gravity in Einstein's general relativity.[8]
References
- ↑ "The Astronomer". 16 April 2013. https://www.questacon.edu.au/visiting/galleries/outdoor/exhibits/the-astronomer.
- ↑ Terence Tao. "Cosmic distance ladder". https://terrytao.files.wordpress.com/2010/10/cosmic-distance-ladder.pdf.
- ↑ Ash, M. E.; Shapiro, I. I.; Smith, W. B. (1967). "Astronomical constants and planetary ephemerides deduced from radar and optical observations". The Astronomical Journal 72: 338. doi:10.1086/110230. Bibcode: 1967AJ.....72..338A.
- ↑ Fernie, J. D. (December 1969). "The Period-Luminosity Relation: A Historical Review". Publications of the Astronomical Society of the Pacific 81 (483): 707. doi:10.1086/128847. ISSN 0004-6280. Bibcode: 1969PASP...81..707F.
- ↑ "Finding the Distance to Stars - Distance Modulus". Australia Telescope National Facility. https://www.atnf.csiro.au/outreach/education/senior/astrophysics/photometry_magnitude.html#magndistance.
- ↑ "Type Ia Supernova". Weekly Topic. Caglow. http://www.caglow.com/info/wtopic/typeia.
- ↑ 7.0 7.1 Holz, Daniel E.; Hughes, Scott A.; Schutz, Bernard F. (December 2018). "Measuring cosmic distances with standard sirens". Physics Today 71 (12): 34–40. doi:10.1063/PT.3.4090. ISSN 0031-9228. Bibcode: 2018PhT....71l..34H.
- ↑ Forward, Robert L.; Berman, David (12 June 1967). "Gravitational-Radiation Detection Range for Binary Stellar Systems" (in en). Physical Review Letters 18 (24): 1071–1074. doi:10.1103/PhysRevLett.18.1071. ISSN 0031-9007. Bibcode: 1967PhRvL..18.1071F.
- ↑ 9.0 9.1 9.2 Schutz, Bernard F. (25 September 1986). "Determining the Hubble constant from gravitational wave observations". Nature 323 (6086): 310–311. doi:10.1038/323310a0. ISSN 0028-0836. Bibcode: 1986Natur.323..310S. http://resolver.caltech.edu/CaltechAUTHORS:20130722-074344394.
- ↑ Hendry, Martin; Woan, Graham (February 2007). "Gravitational astrophysics". Astronomy & Geophysics 48 (1): 1.10–1.17. doi:10.1111/j.1468-4004.2007.48110.x. Bibcode: 2007A&G....48a..10H. https://www.ligo.caltech.edu/~ajw/IntroPapers/hendry01_GWastrophysics.pdf. Retrieved 2019-08-04.
- ↑ Nissanke, Samaya; Holz, Daniel E.; Hughes, Scott A.; Dalal, Neal; Sievers, Jonathan L. (2010-12-10). "Exploring Short Gamma-Ray Bursts as Gravitational-Wave Standard Sirens". The Astrophysical Journal 725 (1): 496–514. doi:10.1088/0004-637X/725/1/496. ISSN 0004-637X. Bibcode: 2010ApJ...725..496N.
- ↑ Abbott, B. P. (16 October 2017). "A gravitational-wave standard siren measurement of the Hubble constant". Nature 551 (7678): 85–88. doi:10.1038/nature24471. PMID 29094696. Bibcode: 2017Natur.551...85A.
- ↑ Marinoni, C. (2008). "Geometrical tests of cosmological models. I. Probing dark energy using the kinematics of high redshift galaxies". Astronomy and Astrophysics 478 (1): 43–55. doi:10.1051/0004-6361:20077116. Bibcode: 2008A&A...478...43M. https://www.research.manchester.ac.uk/portal/en/publications/a-gravitationalwave-standard-siren-measurement-of-the-hubble-constant(f8b9915b-5717-45bc-acea-54e277df11a1).html. Retrieved 2019-10-23.
- ↑ "Light echoes whisper the distance to a star" (Press release). European Southern Observatory. 11 February 2008. Archived from the original on 2015-09-24. Retrieved 2015-10-18.
- ↑ Kervella, Pierre; Mérand, Antoine; Szabados, László; Fouqué, Pascal; Bersier, David; Pompei, Emanuela; Perrin, Guy (2 March 2008). "The long-period Galactic Cepheid RS Puppis I. A geometric distance from its light echoes". Astronomy and Astrophysics 480 (1): 167–178. doi:10.1051/0004-6361:20078961. Bibcode: 2008A&A...480..167K. "we derive a geometric distance of 1992±28 pc to RS Pup".
- ↑ Bond, Howard E.; Sparks, William B. (4 March 2009). "On geometric distance determination to the Cepheid RS Puppis from its light echoes". Astronomy and Astrophysics 495 (2): 371–377. doi:10.1051/0004-6361:200810280. Bibcode: 2009A&A...495..371B. "We conclude that most of the knots are in fact likely to lie in front of the plane of the sky, thus invalidating the Kervella et al. result. [...] Although the Kervella et al. distance result is invalidated, we show that high-resolution polarimetric imaging has the potential to yield a valid geometric distance to this important Cepheid.".
- ↑ Kervella, Pierre; Bond, Howard E.; Cracraft, Misty; Szabados, László; Breitfelder, Joanne; Mérand2, Antoine; Sparks, William B.; Gallenne, Alexandre et al. (December 2014). "The long-period Galactic Cepheid RS Puppis. III. A geometric distance from HST polarimetric imaging of its light echoes". Astronomy and Astrophysics 572: A7 (13 pp.). doi:10.1051/0004-6361/201424395. Bibcode: 2014A&A...572A...7K. "We obtain a distance of 1910±80 pc (4.2%)".
- ↑ Bonanos, A. Z. (2006). "Eclipsing Binaries: Tools for Calibrating the Extragalactic Distance Scale". Proceedings of IAU Symposium 240: 79–87. doi:10.1017/S1743921307003845. Bibcode: 2007IAUS..240...79B.
- ↑ Ferrarese, L (2000). "A Database of Cepheid Distance Moduli and Tip of the Red Giant Branch, Globular Cluster Luminosity Function, Planetary Nebula Luminosity Function, and Surface Brightness Fluctuation Data Useful for Distance Determinations". The Astrophysical Journal Supplement Series 128 (2): 431–459. doi:10.1086/313391. Bibcode: 2000ApJS..128..431F.
- ↑ Colgate, S. A. (1979). "Supernovae as a standard candle for cosmology". Astrophysical Journal 232 (1): 404–408. doi:10.1086/157300. Bibcode: 1979ApJ...232..404C.
- ↑ Adapted from George H. Jacoby; David Branch; Robin Ciardullo; Roger L. Davies; William E. Harris; Michael J. Pierce; Christopher J. Pritchet; John L. Tonry et al. (1992). "A critical review of selected techniques for measuring extragalactic distances". Publications of the Astronomical Society of the Pacific 104 (678): 599–662. doi:10.1086/133035. Bibcode: 1992PASP..104..599J.
- ↑ Benedict, G. Fritz et al. "Hubble Space Telescope Fine Guidance Sensor Parallaxes of Galactic Cepheid Variable Stars: Period-Luminosity Relations" , The Astronomical Journal, Volume 133, Issue 4, pp. 1810–1827 (2007)
- ↑ Majaess, Daniel; Turner, David; Moni Bidin, Christian; Mauro, Francesco; Geisler, Douglas; Gieren, Wolfgang; Minniti, Dante; Chené, André-Nicolas; Lucas, Philip; Borissova, Jura; Kurtev, Radostn; Dékány, Istvan; Saito, Roberto K. "New Evidence Supporting Membership for TW Nor in Lyngå 6 and the Centaurus Spiral Arm" , ApJ Letters, Volume 741, Issue 2, article id. L2 (2011)
- ↑ Stanek, K. Z.; Udalski, A. (1999). "The Optical Gravitational Lensing Experiment. Investigating the Influence of Blending on the Cepheid Distance Scale with Cepheids in the Large Magellanic Cloud". arXiv:astro-ph/9909346.
- ↑ Udalski, A.; Wyrzykowski, L.; Pietrzynski, G.; Szewczyk, O.; Szymanski, M.; Kubiak, M.; Soszynski, I.; Zebrun, K. (2001). "The Optical Gravitational Lensing Experiment. Cepheids in the Galaxy IC1613: No Dependence of the Period-Luminosity Relation on Metallicity". Acta Astronomica 51: 221. Bibcode: 2001AcA....51..221U.
- ↑ Ngeow, C.; Kanbur, S. M. (2006). "The Hubble Constant from Type Ia Supernovae Calibrated with the Linear and Nonlinear Cepheid Period-Luminosity Relations". The Astrophysical Journal 642 (1): L29. doi:10.1086/504478. Bibcode: 2006ApJ...642L..29N.
- ↑ Macri, L. M.; Stanek, K. Z.; Bersier, D.; Greenhill, L. J.; Reid, M. J. (2006). "A New Cepheid Distance to the Maser–Host Galaxy NGC 4258 and Its Implications for the Hubble Constant". The Astrophysical Journal 652 (2): 1133–1149. doi:10.1086/508530. Bibcode: 2006ApJ...652.1133M.
- ↑ Bono, G.; Caputo, F.; Fiorentino, G.; Marconi, M.; Musella, I. (2008). "Cepheids in External Galaxies. I. The Maser–Host Galaxy NGC 4258 and the Metallicity Dependence of Period–Luminosity and Period–Wesenheit Relations". The Astrophysical Journal 684 (1): 102. doi:10.1086/589965. Bibcode: 2008ApJ...684..102B.
- ↑ Majaess, D.; Turner, D.; Lane, D. (2009). "Type II Cepheids as Extragalactic Distance Candles". Acta Astronomica 59 (4): 403. Bibcode: 2009AcA....59..403M.
- ↑ Madore, Barry F.; Freedman, Wendy L. (2009). "Concerning the Slope of the Cepheid Period–Luminosity Relation". The Astrophysical Journal 696 (2): 1498–1501. doi:10.1088/0004-637X/696/2/1498. Bibcode: 2009ApJ...696.1498M.
- ↑ Scowcroft, V.; Bersier, D.; Mould, J. R.; Wood, P. R. (2009). "The effect of metallicity on Cepheid magnitudes and the distance to M33". Monthly Notices of the Royal Astronomical Society 396 (3): 43–47. doi:10.1111/j.1365-2966.2009.14822.x. Bibcode: 2009MNRAS.396.1287S.
- ↑ Majaess, D. (2010). "The Cepheids of Centaurus A (NGC 5128) and Implications for H0". Acta Astronomica 60 (2): 121. Bibcode: 2010AcA....60..121M.
- ↑ Tammann, G. A.; Sandage, A.; Reindl, B. (2008). "The expansion field: The value of H 0". Annual Review of Astronomy and Astrophysics 15 (4): 289. doi:10.1007/s00159-008-0012-y. Bibcode: 2008A&ARv..15..289T.
- ↑ Freedman, Wendy L.; Madore, Barry F. (2010). "The Hubble Constant". Annual Review of Astronomy and Astrophysics 48: 673–710. doi:10.1146/annurev-astro-082708-101829. Bibcode: 2010ARA&A..48..673F.
- ↑ Coelho, R. et al. (2015). "Standardization of type Ia supernovae". European Journal of Physics 36 (1): 015007. doi:10.1088/0143-0807/36/1/015007. Bibcode: 2015EJPh...36a5007C.
- ↑ Tonry, John L.; Dressler, Alan; Blakeslee, John P.; Ajhar, Edward A.; Fletcher, Andre B.; Luppino, Gerard A.; Metzger, Mark R.; Moore, Christopher B. (2001), "The SBF Survey of Galaxy Distances. IV. SBF Magnitudes, Colors, and Distances", Astrophysical Journal 546 (2): 681–693, doi:10.1086/318301, Bibcode: 2001ApJ...546..681T
- ↑ Dressler, Alan (1987). "The Dn-sigma relation for bulges of disk galaxies - A new, independent measure of the Hubble constant" (in en). The Astrophysical Journal 317: 1. doi:10.1086/165251. ISSN 0004-637X. Bibcode: 1987ApJ...317....1D.
- ↑ Gilfanov, Marat; Bogdán, Ákos (2010). "An upper limit on the contribution of accreting white dwarfs to the type Ia supernova rate". Nature 463 (3): 924–925. doi:10.1038/nature08685. PMID 20164924. Bibcode: 2010Natur.463..924G.
Bibliography
- Carroll, Bradley W.; Ostlie, Dale A. (2014). An Introduction to Modern Astrophysics. Harlow, United Kingdom: Pearson Education Limited. ISBN 978-1-292-02293-2.
- Measuring the Universe The Cosmological Distance Ladder, Stephen Webb, copyright 2001.
- Pasachoff, J.M.; Filippenko, A. (2013). The Cosmos: Astronomy in the New Millennium (4th ed.). Cambridge: Cambridge University Press. ISBN 978-1-107-68756-1. https://books.google.com/books?id=tZsoAAAAQBAJ.
- The Astrophysical Journal, The Globular Cluster Luminosity Function as a Distance Indicator: Dynamical Effects, Ostriker and Gnedin, May 5, 1997.
- An Introduction to Distance Measurement in Astronomy, Richard de Grijs, Chichester: John Wiley & Sons, 2011, ISBN:978-0-470-51180-0.
External links
- The ABC's of distances (UCLA)
- The Extragalactic Distance Scale by Bill Keel
- The Hubble Space Telescope Key Project on the Extragalactic Distance Scale
- The Hubble Constant, a historical discussion
- NASA Cosmic Distance Scale
- PNLF information database
- The Astrophysical Journal
 |


