Physics:History of quantum mechanics

Short description: none

10 of the most influential figures in the history of quantum mechanics. Left to right: Max Planck, Albert Einstein, Niels Bohr, Louis de Broglie, Max Born, Paul Dirac, Werner Heisenberg, Wolfgang Pauli, Erwin Schrödinger, Richard Feynman.

The history of quantum mechanics is a fundamental part of the history of modern physics. The major chapters of this history begin with the emergence of quantum ideas to explain individual phenomena—blackbody radiation, the photoelectric effect, solar emission spectra—an era called the Old or Older quantum theories. Building on the technology developed in classical mechanics, the invention of wave mechanics by Erwin Schrödinger and expansion by many others triggers the "modern" era beginning around 1925. Paul Dirac's relativistic quantum theory work lead him to explore quantum theories of radiation, culminating in quantum electrodynamics, the first quantum field theory. The history of quantum mechanics continues in the history of quantum field theory. The history of quantum chemistry, theoretical basis of chemical structure, reactivity, and bonding, interlaces with the events discussed in this article.

The phrase "quantum mechanics" was coined (in German, Quantenmechanik) by the group of physicists including Max Born, Werner Heisenberg, and Wolfgang Pauli, at the University of Göttingen in the early 1920s, and was first used in Born's 1925 paper "Zur Quantenmechanik".

The word quantum comes from the Latin word for "how much" (as does quantity). Something that is quantized, as the energy of Planck's harmonic oscillators, can only take specific values. For example, in most countries, money is effectively quantized, with the quantum of money being the lowest-value coin in circulation. Mechanics is the branch of science that deals with the action of forces on objects. So, quantum mechanics is the part of mechanics that deals with objects for which particular properties are quantized.

Triumph and trouble at the end of the classical era

The discoveries of the 19th century, both the successes and failures, set the stage for the emergence of quantum mechanics.

Wave theory of light

Beginning in 1670 and progressing over three decades, Isaac Newton developed and championed his corpuscular theory, arguing that the perfectly straight lines of reflection demonstrated light's particle nature, as at that time no wave theory demonstrated travel in straight lines. He explained refraction by positing that particles of light accelerated laterally upon entering a denser medium. Around the same time, Newton's contemporaries Robert Hooke and Christiaan Huygens, and later Augustin-Jean Fresnel, mathematically refined the wave viewpoint, showing that if light traveled at different speeds in different media, refraction could be easily explained as the medium-dependent propagation of light waves. The resulting Huygens–Fresnel principle was extremely successful at reproducing light's behaviour and was consistent with Thomas Young's discovery of wave interference of light by his double-slit experiment in 1801. The wave view did not immediately displace the ray and particle view, but began to dominate scientific thinking about light in the mid 19th century, since it could explain polarization phenomena that the alternatives could not.

James Clerk Maxwell discovered that he could apply his previously discovered Maxwell's equations, along with a slight modification to describe self-propagating waves of oscillating electric and magnetic fields. It quickly became apparent that visible light, ultraviolet light, and infrared light were all electromagnetic waves of differing frequency. This theory became a critical ingredient in the beginning of quantum mechanics.

Emerging atomic theory

During the early 19th century, chemical research by John Dalton and Amedeo Avogadro lent weight to the atomic theory of matter, an idea that James Clerk Maxwell, Ludwig Boltzmann and others built upon to establish the kinetic theory of gases. The successes of kinetic theory gave further credence to the idea that matter is composed of atoms, yet the theory also had shortcomings that would only be resolved by the development of quantum mechanics. The existence of atoms was not universally accepted among physicists or chemists; Ernst Mach, for example, was a staunch anti-atomist.

Ludwig Boltzmann's diagram of the I₂ molecule proposed in 1898 showing the atomic "sensitive region" (α, β) of overlap.

Ludwig Boltzmann suggested in 1877 that the energy levels of a physical system, such as a molecule, could be discrete (rather than continuous). Boltzmann's rationale for the presence of discrete energy levels in molecules such as those of iodine gas had its origins in his statistical thermodynamics and statistical mechanics theories and was backed up by mathematical arguments, as would also be the case twenty years later with the first quantum theory put forward by Max Planck.

Electrons

In the final days of the 1800s, J. J. Thomson established that electrons carry a negative charge opposite but the same size as that of a hydrogen ion while having a mass over one thousand times less. Many such electrons were known to be associated with every atom.

Radiation theory

With decreasing temperature, the peak of the blackbody radiation curve shifts to longer wavelengths and also has lower intensities. The blackbody radiation curves (1862) at left are also compared with the early, classical limit model of Rayleigh and Jeans (1900) shown at right. The short wavelength side of the curves was already approximated in 1896 by the Wien distribution law.

Throughout the 1800s many studies investigated details in the spectrum of intensity versus frequency for light emitted by flames, by the Sun, or red-hot objects. Rydberg's formula effectively summarized the dark lines seen in the spectrum, but the provided no physical model to explain them. The spectrum emitted by red-hot objects could be explained at high or low wavelengths but the two theories differed.

Old quantum theory

Quantum mechanics developed in two distinct phases. The first phase, known as the old quantum theory, began around 1900 with radically new approaches to explanations physical phenomena not understood by classical mechanics of the 1800s.

Max Planck introduces quanta to explain black-body radiation

A side portrait of Planck as a young adult, c. 1878

Hot metalwork. The yellow-orange glow is the visible part of the thermal radiation emitted due to the high temperature. Everything else in the picture is glowing with thermal radiation as well, but less brightly and at longer wavelengths than the human eye can detect. A far-infrared camera can observe this radiation.

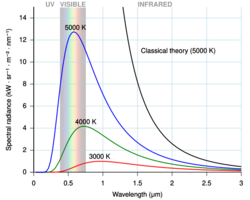
Thermal radiation is electromagnetic radiation emitted from the surface of an object due to the object's internal energy. If an object is heated sufficiently, it starts to emit light at the red end of the visible spectrum, as it becomes red hot.

Heating it further causes the color to change from red to yellow, white, and blue, as it emits light at increasingly shorter wavelengths (higher frequencies). A perfect emitter is also a perfect absorber: when it is cold, such an object looks perfectly black, because it absorbs all the light that falls on it and emits none. Consequently, an ideal thermal emitter is known as a black body, and the radiation it emits is called black-body radiation.

Predictions of the amount of thermal radiation of different frequencies emitted by a body. Correct values predicted by Planck's law (green) contrasted against the classical values of Rayleigh-Jeans law (red) and Wien approximation (blue).

By the late 19th century, thermal radiation had been fairly well characterized experimentally. Several formulas had been created that could describe some of the experimental measurements of thermal radiation: how the wavelength at which the radiation is strongest changes with temperature is given by Wien's displacement law, the overall power emitted per unit area is given by the Stefan–Boltzmann law. The best theoretical explanation of the experimental results was the Rayleigh–Jeans law, which agrees with experimental results well at large wavelengths (or, equivalently, low frequencies), but strongly disagrees at short wavelengths (or high frequencies). In fact, at short wavelengths, classical physics predicted that energy will be emitted by a hot body at an infinite rate. This result, which is clearly wrong, is known as the ultraviolet catastrophe. However, classical physics led to the Rayleigh–Jeans law, which, as shown in the figure, agrees with experimental results well at low frequencies, but strongly disagrees at high frequencies. Physicists searched for a single theory that explained all the experimental results.

Black-body radiation intensity vs color and temperature. The rainbow bar represents visible light; 5000K objects are "white hot" by mixing differing colors of visible light. To the right is the invisible infrared. Classical theory (black curve for 5000K) fails; the other curves are correct predicted by Planck's law.

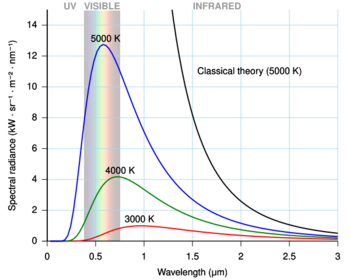
The first model that was able to explain the full spectrum of thermal radiation was put forward by Max Planck in 1900. He proposed a mathematical model in which the thermal radiation was in equilibrium with a set of harmonic oscillators. To reproduce the experimental results, he had to assume that each oscillator emitted an integer number of units of energy at its single characteristic frequency, rather than being able to emit any arbitrary amount of energy. In other words, the energy emitted by an oscillator was quantized. The quantum of energy for each oscillator, according to Planck, was proportional to the frequency of the oscillator; the constant of proportionality is now known as the Planck constant.

Planck's law was the first quantum theory in physics, and Planck won the Nobel Prize in 1918 "in recognition of the services he rendered to the advancement of Physics by his discovery of energy quanta". At the time, however, Planck's view was that quantization was purely a heuristic mathematical construct, rather than (as is now believed) a fundamental change in our understanding of the world.

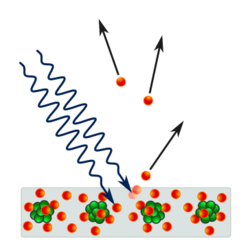
Albert Einstein applies quanta to explain the photoelectric effect

Light is shone upon the surface from the left. If the light frequency is high enough, i.e. if it delivers sufficient energy, negatively charged electrons are ejected from the metal.

In 1887, Heinrich Hertz observed that when light with sufficient frequency hits a metallic surface, the surface emits cathode rays. Ten years later, J. J. Thomson showed that the many reports of cathode rays were actually "corpuscles" and they quickly came to be called electrons. In 1902, Philipp Lenard discovered that the maximum possible energy of an ejected electron is unrelated to its intensity. This observation is at odds with classical electromagnetism, which predicts that the electron's energy should be proportional to the intensity of the incident radiation.

Albert Einstein c. 1905

In 1905, Albert Einstein suggested that even though continuous models of light worked extremely well for time-averaged optical phenomena, for instantaneous transitions the energy in light may occur a finite number of energy quanta. From the introduction section of his March 1905 quantum paper "On a heuristic viewpoint concerning the emission and transformation of light", Einstein states:

According to the assumption to be contemplated here, when a light ray is spreading from a point, the energy is not distributed continuously over ever-increasing spaces, but consists of a finite number of "energy quanta" that are localized in points in space, move without dividing, and can be absorbed or generated only as a whole.

This statement has been called the most revolutionary sentence written by a physicist of the twentieth century. The energy of a single quantum of light of frequency [math]\displaystyle{ f }[/math] is given by the frequency multiplied by Planck's constant [math]\displaystyle{ h }[/math] (an extremely tiny positive number):

[math]\displaystyle{ E = hf }[/math]

Einstein assumed a light quanta transfers all of its energy to a single electron imparting at most an energy hf to the electron. Therefore, only the light frequency determines the maximum energy that can be imparted to the electron; the intensity of the photoemission is proportional to the light beam intensity.

Einstein argued that it takes a certain amount of energy, called the work function and denoted by φ, to remove an electron from the metal. This amount of energy is different for each metal. If the energy of the light quanta is less than the work function, then it does not carry sufficient energy to remove the electron from the metal. The threshold frequency, f₀, is the frequency of a light quanta whose energy is equal to the work function:

[math]\displaystyle{ \varphi = h f_0. }[/math]

If f is greater than f₀, the energy hf is enough to remove an electron. The ejected electron has a kinetic energy, E_K, which is, at most, equal to the light energy minus the energy needed to dislodge the electron from the metal:

[math]\displaystyle{ E_K = hf - \varphi = h(f - f_0). }[/math]

Einstein's description of light as being composed of energy quanta extended Planck's notion of quantized energy, which is that a single quanta of a given frequency, f, delivers an invariant amount of energy, hf. In nature, single quanta are rarely encountered. The Sun and emission sources available in the 19th century emit vast amount of energy every second. Planck's constant, h, is so tiny that the amount of energy in each quanta, hf is very very small. Light we see includes many trillions of such quanta.

The quantization of matter: the Bohr model of the atom

By the dawn of the 20th century, the evidence required a model of the atom with a diffuse cloud of negatively charged electrons surrounding a small, dense, positively charged nucleus. These properties suggested a model in which electrons circle the nucleus like planets orbiting a star. The classical model of the atom is called the planetary model, or sometimes the Rutherford model—after Ernest Rutherford who proposed it in 1911, based on the Geiger–Marsden gold foil experiment, which first demonstrated the existence of the nucleus. However, it was also known that the atom in this model would be unstable: according to classical theory, orbiting electrons are undergoing centripetal acceleration, and should therefore give off electromagnetic radiation, the loss of energy also causing them to spiral toward the nucleus, colliding with it in a fraction of a second.

A second, related puzzle was the emission spectrum of atoms. When a gas is heated, it gives off light only at discrete frequencies. For example, the visible light given off by hydrogen consists of four different colors, as shown in the picture below. The intensity of the light at different frequencies is also different. By contrast, white light consists of a continuous emission across the whole range of visible frequencies. By the end of the nineteenth century, a simple rule known as Balmer's formula showed how the frequencies of the different lines related to each other, though without explaining why this was, or making any prediction about the intensities. The formula also predicted some additional spectral lines in ultraviolet and infrared light that had not been observed at the time. These lines were later observed experimentally, raising confidence in the value of the formula.

Emission spectrum of hydrogen. When excited, hydrogen gas gives off light in four distinct colors (spectral lines) in the visible spectrum, as well as a number of lines in the infrared and ultraviolet.

The mathematical formula describing hydrogen's emission spectrum

In 1885 the Swiss mathematician Johann Balmer discovered that each wavelength λ (lambda) in the visible spectrum of hydrogen is related to some integer n by the equation

[math]\displaystyle{ \lambda = B\left(\frac{n^2}{n^2-4}\right) \qquad\qquad n = 3,4,5,6 }[/math]

where B is a constant Balmer determined is equal to 364.56 nm.

In 1888 Johannes Rydberg generalized and greatly increased the explanatory utility of Balmer's formula. He predicted that λ is related to two integers n and m according to what is now known as the Rydberg formula:

[math]\displaystyle{ \frac{1}{\lambda} = R \left(\frac{1}{m^2} - \frac{1}{n^2}\right), }[/math]

where R is the Rydberg constant, equal to 0.0110 nm⁻¹, and n must be greater than m.

Rydberg's formula accounts for the four visible wavelengths of hydrogen by setting m = 2 and n = 3, 4, 5, 6. It also predicts additional wavelengths in the emission spectrum: for m = 1 and for n > 1, the emission spectrum should contain certain ultraviolet wavelengths, and for m = 3 and n > 3, it should also contain certain infrared wavelengths. Experimental observation of these wavelengths came two decades later: in 1908 Louis Paschen found some of the predicted infrared wavelengths, and in 1914 Theodore Lyman found some of the predicted ultraviolet wavelengths.

Both Balmer and Rydberg's formulas involve integers: in modern terms, they imply that some property of the atom is quantized. Understanding exactly what this property was, and why it was quantized, was a major part of the development of quantum mechanics, as shown in the rest of this article.

In 1905, Albert Einstein used kinetic theory to explain Brownian motion. French physicist Jean Baptiste Perrin used the model in Einstein's paper to experimentally determine the mass, and the dimensions, of atoms, thereby giving direct empirical verification of the atomic theory.

Niels Bohr's 1913 quantum model of the hydrogen atom.

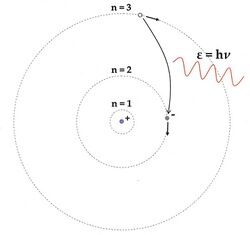
In 1913 Niels Bohr proposed a new model of the atom that included quantized electron orbits: electrons still orbit the nucleus much as planets orbit around the Sun, but they are permitted to inhabit only certain orbits, not to orbit at any arbitrary distance. When an atom emitted (or absorbed) energy, the electron did not move in a continuous trajectory from one orbit around the nucleus to another, as might be expected classically. Instead, the electron would jump instantaneously from one orbit to another, giving off the emitted light in the form of a photon. The possible energies of photons given off by each element were determined by the differences in energy between the orbits, and so the emission spectrum for each element would contain a number of lines.

Niels Bohr as a young man

Starting from only one simple assumption about the rule that the orbits must obey, the Bohr model was able to relate the observed spectral lines in the emission spectrum of hydrogen to previously known constants. In Bohr's model, the electron was not allowed to emit energy continuously and crash into the nucleus: once it was in the closest permitted orbit, it was stable forever. Bohr's model did not explain why the orbits should be quantized in that way, nor was it able to make accurate predictions for atoms with more than one electron, or to explain why some spectral lines are brighter than others.

Some fundamental assumptions of the Bohr model were soon proven wrong—but the key result that the discrete lines in emission spectra are due to some property of the electrons in atoms being quantized is correct. The way that the electrons actually behave is strikingly different from Bohr's atom, and from what we see in the world of our everyday experience; this modern quantum mechanical model of the atom is discussed below.

A more detailed explanation of the Bohr model

Bohr theorized that the angular momentum, L, of an electron is quantized:

[math]\displaystyle{ L = n\frac{h}{2\pi}=n\hbar }[/math]

where n is an integer and h and ħ are the Planck constant and Planck reduced constant respectively. Starting from this assumption, Coulomb's law and the equations of circular motion show that an electron with n units of angular momentum orbits a proton at a distance r given by

[math]\displaystyle{ r = \frac{n^2 h^2}{4 \pi^2 k_e m e^2} }[/math],

where k_e is the Coulomb constant, m is the mass of an electron, and e is the charge on an electron. For simplicity this is written as

[math]\displaystyle{ r = n^2 a_0,\! }[/math]

where a₀, called the Bohr radius, is equal to 0.0529 nm. The Bohr radius is the radius of the smallest allowed orbit.

The energy of the electron is the sum of its kinetic and potential energies. The electron has kinetic energy by virtue of its actual motion around the nucleus, and potential energy because of its electromagnetic interaction with the nucleus. In the Bohr model this energy can be calculated, and is given by

[math]\displaystyle{ E = -\frac{k_{\mathrm{e}}e^2}{2a_0} \frac{1}{n^2} }[/math].

Thus Bohr's assumption that angular momentum is quantized means that an electron can inhabit only certain orbits around the nucleus and that it can have only certain energies. A consequence of these constraints is that the electron does not crash into the nucleus: it cannot continuously emit energy, and it cannot come closer to the nucleus than a₀ (the Bohr radius).

An electron loses energy by jumping instantaneously from its original orbit to a lower orbit; the extra energy is emitted in the form of a photon. Conversely, an electron that absorbs a photon gains energy, hence it jumps to an orbit that is farther from the nucleus.

Each photon from glowing atomic hydrogen is due to an electron moving from a higher orbit, with radius r_n, to a lower orbit, r_m. The energy E_γ of this photon is the difference in the energies E_n and E_m of the electron:

[math]\displaystyle{ E_{\gamma} = E_n - E_m = \frac{k_{\mathrm{e}}e^2}{2a_0}\left(\frac{1}{m^2}-\frac{1}{n^2}\right) }[/math]

Since Planck's equation shows that the photon's energy is related to its wavelength by E_γ = hc/λ, the wavelengths of light that can be emitted are given by

[math]\displaystyle{ \frac{1}{\lambda} = \frac{k_{\mathrm{e}}e^2}{2 a_0 h c}\left(\frac{1}{m^2}-\frac{1}{n^2}\right). }[/math]

This equation has the same form as the Rydberg formula, and predicts that the constant R should be given by

[math]\displaystyle{ R = \frac{k_{\mathrm{e}}e^2}{2 a_0 h c} . }[/math]

Therefore, the Bohr model of the atom can predict the emission spectrum of hydrogen in terms of fundamental constants. The model can be easily modified to account for the emission spectrum of any system consisting of a nucleus and a single electron (that is, ions such as He⁺ or O⁷⁺, which contain only one electron) but cannot be extended to an atom with two electrons such as neutral helium. However, it was not able to make accurate predictions for multi-electron atoms, or to explain why some spectral lines are brighter than others.

An important step was taken in the evolution of quantum theory at the first Solvay Congress of 1911. There the top physicists of the scientific community met to discuss the problem of “Radiation and the Quanta.” By this time the Ernest Rutherford model of the atom had been published, but much of the discussion involving atomic structure revolved around the quantum model of Arthur Haas in 1910. Also, at the Solvay Congress in 1911 Hendrik Lorentz suggested after Einstein's talk on quantum structure that the energy of a rotator be set equal to nhv. This was followed by other quantum models such as the John William Nicholson model of 1912 which was nuclear and discretized angular momentum. Nicholson had introduced the spectra into his atomic model by using the oscillations of electrons in a nuclear atom perpendicular to the orbital plane thereby maintaining stability. Nicholson's atomic spectra identified many unattributed lines in solar and nebular spectra.

In 1913, Bohr explained the spectral lines of the hydrogen atom, again by using quantization, in his paper of July 1913 On the Constitution of Atoms and Molecules in which he discussed and cited the Nicholson model. In the Bohr model, the hydrogen atom is pictured as a heavy, positively charged nucleus orbited by a light, negatively charged electron. The electron can only exist in certain, discretely separated orbits, labeled by their angular momentum, which is restricted to be an integer multiple of the reduced Planck constant. The model's key success lay in explaining the Rydberg formula for the spectral emission lines of atomic hydrogen by using the transitions of electrons between orbits. While the Rydberg formula had been known experimentally, it did not gain a theoretical underpinning until the Bohr model was introduced. Not only did the Bohr model explain the reasons for the structure of the Rydberg formula, it also provided a justification for the fundamental physical constants that make up the formula's empirical results.

Moreover, the application of Planck's quantum theory to the electron allowed Ștefan Procopiu in 1911–1913, and subsequently Niels Bohr in 1913, to calculate the magnetic moment of the electron, which was later called the "magneton"; similar quantum computations, but with numerically quite different values, were subsequently made possible for both the magnetic moments of the proton and the neutron that are three orders of magnitude smaller than that of the electron.

These theories, though successful, were strictly phenomenological: during this time, there was no rigorous justification for quantization, aside, perhaps, from Henri Poincaré's discussion of Planck's theory in his 1912 paper Sur la théorie des quanta. They are collectively known as the old quantum theory.

Spin quantization

File:Quantum spin and the Stern-Gerlach experiment.ogv Quantization of the orbital angular momentum of the electron combined with the magnetic moment of the electron suggested that atoms with a magnetic moment should show quantized behavior in a magnetic field. In 1922, Otto Stern and Walther Gerlach set out to test this theory. They heated silver in a vacuum tube equipped with a series of narrow aligned slits, creating a molecular beam of silver atoms. They shot this beam through an inhomogeneous magnetic field. Rather than a continuous pattern of Silver atoms, they found two bunches.

Relative to its northern pole, pointing up, down, or somewhere in between, in classical mechanics, a magnet thrown through a magnetic field may be deflected a small or large distance upwards or downwards. The atoms that Stern and Gerlach shot through the magnetic field acted similarly. However, while the magnets could be deflected variable distances, the atoms would always be deflected a constant distance either up or down. This implied that the property of the atom that corresponds to the magnet's orientation must be quantized, taking one of two values (either up or down), as opposed to being chosen freely from any angle.

The choice of the orientation of the magnetic field used in the Stern–Gerlach experiment is arbitrary. In the animation shown here, the field is vertical and so the atoms are deflected either up or down. If the magnet is rotated a quarter turn, the atoms are deflected either left or right. Using a vertical field shows that the spin along the vertical axis is quantized, and using a horizontal field shows that the spin along the horizontal axis is quantized.

The results of the Stern-Gelach experiment caused a sensation, most especially because leading scientists, including Einstein and Paul Ehrenfest argued that the silver atoms should have random orientations in the conditions of the experiment: quantization should not have been observable. At least five years would elapse before this mystery was resolved: quantization was observed but it was not due to orbital angular momentum.

In 1925 Ralph Kronig proposed that electrons behave as if they self-rotate, or "spin", about an axis. Spin would generate a tiny magnetic moment that would split the energy levels responsible for spectral lines, in agreement with existing measurements. Two electrons in the same orbital would occupy distinct quantum states if they "spun" in opposite directions, thus satisfying the exclusion principle. Unfortunately, the theory had two significant flaws: two values computed by Kronig were off by a factor of two. Kronig's senior colleagues discouraged his work and it was never published.

Ten months later, Dutch physicists George Uhlenbeck and Samuel Goudsmit at Leiden University published their theory of electron self rotation. The model, like Kronig's was essentially classical but resulted in a quantum prediction.

de Broglie's matter wave hypothesis

Louis de Broglie in 1929. De Broglie won the Nobel Prize in Physics for his prediction that matter acts as a wave, made in his 1924 PhD thesis.

In 1924 Louis de Broglie published a breakthrough hypothesis: matter has wave properties. Building on Einstein's proposal that the photoelectric effect can be described using quantized energy transfers and by Einstein's separate proposal, from special relativity, that mass at rest is equivalent to energy via [math]\displaystyle{ E=m_0c^2 }[/math], de Broglie proposed that matter in motion appears to have an associated wave with wavelength [math]\displaystyle{ \lambda=h/p }[/math] where [math]\displaystyle{ p }[/math] is the matter momentum from the motion. Requiring his wavelength to encircle an atom, he explained quantization of Bohr's orbits. Simultaneously this showed that the wave behavior of light was essentially a quantum effect.

De Broglie expanded the Bohr model of the atom by showing that an electron in orbit around a nucleus could be thought of as having wave-like properties. In particular, an electron is observed only in situations that permit a standing wave around a nucleus. An example of a standing wave is a violin string, which is fixed at both ends and can be made to vibrate. The waves created by a stringed instrument appear to oscillate in place, moving from crest to trough in an up-and-down motion. The wavelength of a standing wave is related to the length of the vibrating object and the boundary conditions. For example, because the violin string is fixed at both ends, it can carry standing waves of wavelengths [math]\displaystyle{ \frac{2l}{n} }[/math], where l is the length and n is a positive integer. De Broglie suggested that the allowed electron orbits were those for which the circumference of the orbit would be an integer number of wavelengths. The electron's wavelength, therefore, determines that only Bohr orbits of certain distances from the nucleus are possible. In turn, at any distance from the nucleus smaller than a certain value, it would be impossible to establish an orbit. The minimum possible distance from the nucleus is called the Bohr radius. De Broglie's treatment of the Bohr atom was ultimately unsuccessful, but his hypothesis served as a starting point for Schrödinger's wave equation.

Matter behaving as a wave was first demonstrated experimentally for electrons: a beam of electrons can exhibit diffraction, just like a beam of light or a water wave. Three years after de Broglie published his hypothesis two different groups demonstrated electron diffraction. At the University of Aberdeen, George Paget Thomson and Alexander Reid passed a beam of electrons through a thin celluloid film, then later metal films, and observed the predicted interference patterns. (Alexander Reid, who was Thomson's graduate student, performed the first experiments but he died soon after in a motorcycle accident and is rarely mentioned.) At Bell Labs, Clinton Joseph Davisson and Lester Halbert Germer reflected an electron beam from a nickel sample in their experiment, observing well-defined beams predicted by wave models returning form the crystal. De Broglie was awarded the Nobel Prize in Physics in 1929 for his hypothesis; Thomson and Davisson shared the Nobel Prize for Physics in 1937 for their experimental work.

Building on de Broglie's approach, modern quantum mechanics was born in 1925, when the German physicists Werner Heisenberg, Max Born, and Pascual Jordan developed matrix mechanics and the Austrian physicist Erwin Schrödinger invented wave mechanics and the non-relativistic Schrödinger equation as an approximation of the generalised case of de Broglie's theory. Schrödinger subsequently showed that the two approaches were equivalent. The first applications of quantum mechanics to physical systems were the algebraic determination of the hydrogen spectrum by Wolfgang Pauli and the treatment of diatomic molecules by Lucy Mensing.

Development of modern quantum mechanics

The end of the first era of quantum mechanics was triggered by de Broglie's publication of his hypothesis of matter waves, leading to Schrödinger's discovery of wave mechanics for matter. Accurate predictions of the absorption spectrum of hydrogen ensured wide acceptance of the new quantum theory.

Matrix mechanics

In 1925, Werner Heisenberg attempted to solve one of the problems that the Bohr model left unanswered, explaining the intensities of the different lines in the hydrogen emission spectrum. Through a series of mathematical analogies, he wrote out the quantum-mechanical analog for the classical computation of intensities. Shortly afterward, Heisenberg's colleague Max Born realized that Heisenberg's method of calculating the probabilities for transitions between the different energy levels could best be expressed by using the mathematical concept of matrices.

Heisenberg formulated an early version of the uncertainty principle in 1927, analyzing a thought experiment where one attempts to measure an electron's position and momentum simultaneously. However, Heisenberg did not give precise mathematical definitions of what the "uncertainty" in these measurements meant, a step that would be taken soon after by Earle Hesse Kennard, Wolfgang Pauli, and Hermann Weyl.

Wave mechanics

In the first half of 1926, building on de Broglie's hypothesis, Erwin Schrödinger developed the equation that describes the behavior of a quantum-mechanical wave. The mathematical model, called the Schrödinger equation after its creator, is central to quantum mechanics, defines the permitted stationary states of a quantum system, and describes how the quantum state of a physical system changes in time. The wave itself is described by a mathematical function known as a "wave function". Schrödinger said that the wave function provides the "means for predicting the probability of measurement results".

Schrödinger was able to calculate the energy levels of hydrogen by treating a hydrogen atom's electron as a classical wave, moving in a well of the electrical potential created by the proton. This calculation accurately reproduced the energy levels of the Bohr model.

In May 1926, Schrödinger proved that Heisenberg's matrix mechanics and his own wave mechanics made the same predictions about the properties and behavior of the electron; mathematically, the two theories had an underlying common form. Yet the two men disagreed on the interpretation of their mutual theory. For instance, Heisenberg accepted the theoretical prediction of jumps of electrons between orbitals in an atom, but Schrödinger hoped that a theory based on continuous wave-like properties could avoid what he called (as paraphrased by Wilhelm Wien) "this nonsense about quantum jumps". In the end, Heisenberg's approach won out, and quantum jumps were confirmed.

Schrödinger and the wave mechanics of the Niels Bohr Institute

The Niels Bohr Institute in Copenhagen, which was a focal point for researchers in quantum mechanics and related subjects in the 1920s and 1930s. Most of the world's best known theoretical physicists spent time there.

Bohr, Heisenberg, and others tried to explain what these experimental results and mathematical models really mean. The term Copenhagen interpretation has been applied to their views in retrospect, glossing over differences among them. While no definitive statement of "the" Copenhagen interpretation exists, the following ideas are widely seen as characteristic of it.

1. A system is completely described by a quantum state (Heisenberg)
2. How the quantum state changes over time is given by a wave equation, the Schrödinger equation imparting wave characteristics to light and matter.
3. Atomic interactions are discontinuous. (Planck's quantum of action)
4. The description of nature is essentially probabilistic. The probability of an event—for example, where on the screen a particle shows up in the double-slit experiment—is related to the square of the absolute value of the amplitude of its wave function. (Born rule, due to Max Born, which gives a physical meaning to the wave function in the Copenhagen interpretation: the probability amplitude)
5. The values of incompatible pairs of properties of the system cannot be known at the same time. (Heisenberg's uncertainty principle)
6. Matter, like light, exhibits a wave-particle duality. An experiment can demonstrate the particle-like properties of matter, or its wave-like properties; but not both at the same time. (Complementarity principle due to Bohr)
7. Measuring devices are essentially classical devices and measure classical properties such as position and momentum.
8. The quantum mechanical description of large systems should closely approximate the classical description. (Correspondence principle of Bohr and Heisenberg)

Application to the hydrogen atom

Bohr's model of the atom was essentially a planetary one, with the electrons orbiting around the nuclear "sun". However, the uncertainty principle states that an electron cannot simultaneously have an exact location and velocity in the way that a planet does. Instead of classical orbits, electrons are said to inhabit atomic orbitals. An orbital is the "cloud" of possible locations in which an electron might be found, a distribution of probabilities rather than a precise location. Each orbital is three dimensional, rather than the two-dimensional orbit, and is often depicted as a three-dimensional region within which there is a 95 percent probability of finding the electron.

Schrödinger was able to calculate the energy levels of hydrogen by treating a hydrogen atom's electron as a wave, represented by the "wave function" Ψ, in an electric potential well, V, created by the proton. The solutions to Schrödinger's equation are distributions of probabilities for electron positions and locations. Orbitals have a range of different shapes in three dimensions. The energies of the different orbitals can be calculated, and they accurately match the energy levels of the Bohr model.

Within Schrödinger's picture, each electron has four properties:

1. An "orbital" designation, indicating whether the particle-wave is one that is closer to the nucleus with less energy or one that is farther from the nucleus with more energy;
2. The "shape" of the orbital, spherical or otherwise;
3. The "inclination" of the orbital, determining the magnetic moment of the orbital around the z-axis.
4. The "spin" of the electron.

The collective name for these properties is the quantum state of the electron. The quantum state can be described by giving a number to each of these properties; these are known as the electron's quantum numbers. The quantum state of the electron is described by its wave function. The Pauli exclusion principle demands that no two electrons within an atom may have the same values of all four numbers.

The shapes of atomic orbitals. Rows: 1s, 2p, 3d and 4f. From left to right [math]\displaystyle{ m=-l,\ldots, l }[/math]. The colors show the phase of the wave function.

The first property describing the orbital is the principal quantum number, n, which is the same as in Bohr's model. n denotes the energy level of each orbital. The possible values for n are integers:

[math]\displaystyle{ n = 1, 2, 3\ldots }[/math]

The next quantum number, the azimuthal quantum number, denoted l, describes the shape of the orbital. The shape is a consequence of the angular momentum of the orbital. The angular momentum represents the resistance of a spinning object to speeding up or slowing down under the influence of external force. The azimuthal quantum number represents the orbital angular momentum of an electron around its nucleus. The possible values for l are integers from 0 to n − 1 (where n is the principal quantum number of the electron):

[math]\displaystyle{ l = 0, 1, \ldots, n-1. }[/math]

The shape of each orbital is usually referred to by a letter, rather than by its azimuthal quantum number. The first shape (l=0) is denoted by the letter s (a mnemonic being "sphere"). The next shape is denoted by the letter p and has the form of a dumbbell. The other orbitals have more complicated shapes (see atomic orbital), and are denoted by the letters d, f, g, etc.

The third quantum number, the magnetic quantum number, describes the magnetic moment of the electron, and is denoted by m_l (or simply m). The possible values for m_l are integers from −l to l (where l is the azimuthal quantum number of the electron):

[math]\displaystyle{ m_l = -l, -(l-1), \ldots, 0, \ldots, (l-1), l. }[/math]

The magnetic quantum number measures the component of the angular momentum in a particular direction. The choice of direction is arbitrary; conventionally the z-direction is chosen.

The fourth quantum number, the spin quantum number (pertaining to the "orientation" of the electron's spin) is denoted m_s, with values +​¹⁄₂ or −​¹⁄₂.

The chemist Linus Pauling wrote, by way of example:

In the case of a helium atom with two electrons in the 1s orbital, the Pauli Exclusion Principle requires that the two electrons differ in the value of one quantum number. Their values of n, l, and m_l are the same. Accordingly they must differ in the value of m_s, which can have the value of +​¹⁄₂ for one electron and −​¹⁄₂ for the other."

It is the underlying structure and symmetry of atomic orbitals, and the way that electrons fill them, that leads to the organization of the periodic table. The way the atomic orbitals on different atoms combine to form molecular orbitals determines the structure and strength of chemical bonds between atoms.

The field of quantum chemistry was pioneered by physicists Walter Heitler and Fritz London, who published a study of the covalent bond of the hydrogen molecule in 1927. Quantum chemistry was subsequently developed by a large number of workers, including the American theoretical chemist Linus Pauling at Caltech, and John C. Slater into various theories such as Molecular Orbital Theory or Valence Theory.

Dirac, relativity, and development of the formal methods.

Starting around 1927, Paul Dirac began the process of unifying quantum mechanics with special relativity by proposing the Dirac equation for the electron. The Dirac equation achieves the relativistic description of the wavefunction of an electron that Schrödinger failed to obtain. It predicts electron spin and led Dirac to predict the existence of the positron. He also pioneered the use of operator theory, including the influential bra–ket notation, as described in his famous 1930 textbook. During the same period, Hungarian polymath John von Neumann formulated the rigorous mathematical basis for quantum mechanics as the theory of linear operators on Hilbert spaces, as described in his likewise famous 1932 textbook. These, like many other works from the founding period, still stand, and remain widely used.

Quantum field theory

Beginning in 1927, researchers attempted to apply quantum mechanics to fields instead of single particles, resulting in quantum field theories. Early workers in this area include P.A.M. Dirac, W. Pauli, V. Weisskopf, and P. Jordan. This area of research culminated in the formulation of quantum electrodynamics by R.P. Feynman, F. Dyson, J. Schwinger, and S. Tomonaga during the 1940s. Quantum electrodynamics describes a quantum theory of electrons, positrons, and the electromagnetic field, and served as a model for subsequent quantum field theories.

Feynman diagram of gluon radiation in quantum chromodynamics

The theory of quantum chromodynamics was formulated beginning in the early 1960s. The theory as we know it today was formulated by Politzer, Gross and Wilczek in 1975.

Building on pioneering work by Schwinger, Higgs and Goldstone, the physicists Glashow, Weinberg and Salam independently showed how the weak nuclear force and quantum electrodynamics could be merged into a single electroweak force, for which they received the 1979 Nobel Prize in Physics.

Quantum information

Quantum information science developed in the latter decades of the 20th century, beginning with theoretical results like Holevo's theorem, the concept of generalized measurements or POVMs, the proposal of quantum key distribution by Bennett and Brassard, and Shor's algorithm.

Founding experiments

• Thomas Young's double-slit experiment demonstrating the wave nature of light. (c. 1801)
• Henri Becquerel discovers radioactivity. (1896)
• J. J. Thomson's cathode ray tube experiments (discovers the electron and its negative charge). (1897)
• The study of black-body radiation between 1850 and 1900, which could not be explained without quantum concepts.
• The photoelectric effect: Einstein explained this in 1905 (and later received a Nobel prize for it) using the concept of photons, particles of light with quantized energy.
• Robert Millikan's oil-drop experiment, which showed that electric charge occurs as quanta (whole units). (1909)
• Ernest Rutherford's gold foil experiment disproved the plum pudding model of the atom which suggested that the mass and positive charge of the atom are almost uniformly distributed. This led to the planetary model of the atom (1911).
• James Franck and Gustav Hertz's electron collision experiment shows that energy absorption by mercury atoms is quantized. (1914)
• Otto Stern and Walther Gerlach conduct the Stern–Gerlach experiment, which demonstrates the quantized nature of particle spin. (1920)
• Arthur Compton with Compton scattering experiment (1923)
• Clinton Davisson and Lester Germer demonstrate the wave nature of the electron in the electron diffraction experiment. (1927)
• Carl David Anderson with the discovery positron (1932), validated Paul Dirac's theoretical prediction of this particle (1928)
• Lamb–Retherford experiment discovered Lamb shift (1947), which led to the development of quantum electrodynamics.
• Clyde L. Cowan and Frederick Reines confirm the existence of the neutrino in the neutrino experiment. (1955)
• Clauss Jönsson's double-slit experiment with electrons. (1961)
• The quantum Hall effect, discovered in 1980 by Klaus von Klitzing. The quantized version of the Hall effect has allowed for the definition of a new practical standard for electrical resistance and for an extremely precise independent determination of the fine-structure constant.
• The experimental verification of quantum entanglement by John Clauser and Stuart Freedman. (1972)
• The Mach–Zehnder interferometer experiment conducted by Paul Kwiat, Harold Wienfurter, Thomas Herzog, Anton Zeilinger, and Mark Kasevich, providing experimental verification of the Elitzur–Vaidman bomb tester, proving interaction-free measurement is possible. (1994)

See also

• Golden age of physics
• Einstein's thought experiments
• History of quantum field theory
• History of chemistry
• History of molecular theory
• History of thermodynamics
• Timeline of atomic and subatomic physics

Further reading

• Bacciagaluppi, Guido; Valentini, Antony (2009), Quantum theory at the crossroads: reconsidering the 1927 Solvay conference, Cambridge, UK: Cambridge University Press, pp. 9184, ISBN 978-0-521-81421-8, OCLC 227191829, Bibcode: 2006quant.ph..9184B 
• Bernstein, Jeremy (2009), Quantum Leaps, Cambridge, Massachusetts: Belknap Press of Harvard University Press, ISBN 978-0-674-03541-6, https://books.google.com/books?id=j0Me3brYOL0C 
• Greenberger, Daniel, Hentschel, Klaus, Weinert, Friedel (Eds.) Compendium of Quantum Physics. Concepts, Experiments, History and Philosophy, New York: Springer, 2009. ISBN:978-3-540-70626-7.
• Jammer, Max (1966), The conceptual development of quantum mechanics, New York: McGraw-Hill, OCLC 534562 
• Jammer, Max (1974), The philosophy of quantum mechanics: The interpretations of quantum mechanics in historical perspective, New York: Wiley, ISBN 0-471-43958-4, OCLC 969760, https://archive.org/details/philosophyofquan0000jamm 
• A. Whitaker. The New Quantum Age: From Bell's Theorem to Quantum Computation and Teleportation, Oxford University Press, 2011, ISBN:978-0-19-958913-5
• Stephen Hawking. The Dreams that Stuff is Made of, Running Press, 2011, ISBN:978-0-76-243434-3
• A. Douglas Stone. Einstein and the Quantum, the Quest of the Valiant Swabian, Princeton University Press, 2006.

External links

zh:物理学史#量子理论