Chemistry:Phase separation

Short description: Creation of two phases of matter from a single homogenous mixture

See also: Physics:Colloid

Mixing of liquids A and B and subsequent phase separation

When mixed, oil and vinegar will phase-separate

A phase diagram for two isotopes of helium, showing at bottom a range of temperatures and ratios at which they will phase-separate.

Phase separation is the creation of two distinct phases from a single homogeneous mixture. The most common type of phase separation occurs between two immiscible liquids, such as oil and water. This type of phase separation is known as liquid-liquid equilibrium. Colloids are formed by phase separation, though not all phase separations form colloids - for example, oil and water can form separated layers under gravity rather than remaining as microscopic droplets in suspension.

A common form of spontaneous phase separation is termed spinodal decomposition; Cahn–Hilliard equation describes it. Regions of a phase diagram in which phase separation occurs are called miscibility gaps. There are two boundary curves of note: the binodal coexistence curve and the spinodal curve. On one side of the binodal, mixtures are absolutely stable. In between the binodal and the spinodal, mixtures may be metastable: staying mixed (or unmixed) in the absence of some large disturbance. The region beyond the spinodal curve is absolutely unstable, and (if starting from a mixed state) will spontaneously phase-separate.

The upper critical solution temperature (UCST) and the lower critical solution temperature (LCST) are two critical temperatures, above which or below which the components of a mixture are miscible in all proportions. It is rare for systems to have both, but some exist: the nicotine-water system has an LCST of 61 °C and also a UCST of 210 °C at pressures high enough for liquid water to exist at that temperature. The components are therefore miscible in all proportions below 61 °C and above 210 °C (at high pressure), and partially miscible in the interval from 61 to 210 °C.

Physical basis

Mixing is governed by the Gibbs free energy, with phase separation or mixing occurring for whichever case lowers the Gibbs free energy. The free energy $G$ can be decomposed into two parts: $G=H-TS$, with $H$ the enthalpy, $T$ the temperature, and $S$ the entropy. Thus, the change of the free energy in mixing is the sum of the enthalpy of mixing and the entropy of mixing. The enthalpy of mixing is zero for ideal mixtures, and ideal mixtures are enough to describe many common solutions. Thus, in many cases, mixing (or phase separation) is driven primarily by the entropy of mixing. It is generally the case that the entropy will increase whenever a particle (an atom, a molecule) has a larger space to explore; thus, the entropy of mixing is generally positive: the components of the mixture can increase their entropy by sharing a larger common volume.

Several distinct processes then drive phase separation. In one case, the enthalpy of mixing is positive, and the temperature is low: the increase in entropy is insufficient to lower the free energy. In another, considerably rarer case, the entropy of mixing is "unfavorable", that is to say, it is negative. In this case, even if the change in enthalpy is negative, phase separation will still occur unless the temperature is low enough. It is this second case which gives rise to the idea of the lower critical solution temperature.

Phase separation in cold gases

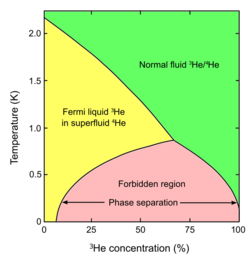
A mixture of two helium isotopes (helium-3 and helium-4) in a certain range of temperatures and concentrations separates into parts. The initial mix of the two isotopes spontaneously separates into ${\phantom{A}}_{\phantom{}}^{\phantom{4}}{\phantom{A}}_{\phantom{2}}^{\phantom{2}4}\mathrm{H}\mathrm{e}$-rich and ${\phantom{A}}_{\phantom{}}^{\phantom{3}}{\phantom{A}}_{\phantom{2}}^{\phantom{2}3}\mathrm{H}\mathrm{e}$-rich regions. Phase separation also exists in ultracold gas systems. It has been shown experimentally in a two-component ultracold Fermi gas case. The phase separation can compete with other phenomena, such as vortex lattice formation or an exotic Fulde-Ferrell-Larkin-Ovchinnikov phase.

See also

• Biomolecular condensate
• Colloid
• Phase diagram
• Phase rule
• UNIQUAC

Further reading

• Khabibullaev, Pulat K.; Saidov, Abdulla (April 2013). Phase Separation in Soft Matter Physics: Micellar Solutions, Microemulsions, Critical Phenomena. Berlin Heidelberg: Springer. ISBN 978-3-662-09278-1.