Chemistry:Stability constants of complexes

Short description: Constants that describe stability of coordination complexes

In coordination chemistry, a stability constant (also called formation constant or binding constant) is an equilibrium constant for the formation of a complex in solution. It is a measure of the strength of the interaction between the reagents that come together to form the complex. There are two main kinds of complex: compounds formed by the interaction of a metal ion with a ligand and supramolecular complexes, such as host–guest complexes and complexes of anions. The stability constant(s) provide(s) the information required to calculate the concentration(s) of the complex(es) in solution. There are many areas of application in chemistry, biology and medicine.

History

Jannik Bjerrum (son of Niels Bjerrum) developed the first general method for the determination of stability constants of metal-ammine complexes in 1941. The reasons why this occurred at such a late date, nearly 50 years after Alfred Werner had proposed the correct structures for coordination complexes, have been summarised by Beck and Nagypál. The key to Bjerrum's method was the use of the then recently developed glass electrode and pH meter to determine the concentration of hydrogen ions in solution. Bjerrum recognised that the formation of a metal complex with a ligand was a kind of acid–base equilibrium: there is competition for the ligand, L, between the metal ion, Mⁿ⁺, and the hydrogen ion, H⁺. This means that there are two simultaneous equilibria that have to be considered. In what follows electrical charges are omitted for the sake of generality. The two equilibria are

[math]\displaystyle{ \mathrm{H + L} \leftrightharpoons \mathrm{HL} }[/math]

[math]\displaystyle{ \mathrm{M + L} \leftrightharpoons \mathrm{ML} }[/math]

Hence by following the hydrogen ion concentration during a titration of a mixture of M and HL with base, and knowing the acid dissociation constant of HL, the stability constant for the formation of ML could be determined. Bjerrum went on to determine the stability constants for systems in which many complexes may be formed.

[math]\displaystyle{ \mathrm{M} + q \mathrm{L} \leftrightharpoons \mathrm{ML}_q }[/math]

The following twenty years saw a veritable explosion in the number of stability constants that were determined. Relationships, such as the Irving-Williams series were discovered. The calculations were done by hand using the so-called graphical methods. The mathematics underlying the methods used in this period are summarised by Rossotti and Rossotti. The next key development was the use of a computer program, LETAGROP to do the calculations. This permitted the examination of systems too complicated to be evaluated by means of hand-calculations. Subsequently, computer programs capable of handling complex equilibria in general, such as SCOGS and MINIQUAD were developed so that today the determination of stability constants has almost become a "routine" operation. Values of thousands of stability constants can be found in two commercial databases.

Theory

The formation of a complex between a metal ion, M, and a ligand, L, is in fact usually a substitution reaction. For example, in aqueous solutions, metal ions will be present as aqua ions, so the reaction for the formation of the first complex could be written as

[math]\displaystyle{ \mathrm{[M(H_2O)}_n] + \mathrm{L} \leftrightharpoons \mathrm{[M(H_2O)}_{n-1}\mathrm{L}] + \mathrm{H_2O} }[/math]

The equilibrium constant for this reaction is given by

[math]\displaystyle{ \beta^'=\frac{[\mathrm{M(H_2O)}_{n-1}\mathrm{L}] [\mathrm{H_2O}]} {[\mathrm{M(H_2O)}_n] [\mathrm{L}] } }[/math]

[L] should be read as "the concentration of L" and likewise for the other terms in square brackets. The expression can be greatly simplified by removing those terms which are constant. The number of water molecules attached to each metal ion is constant. In dilute solutions the concentration of water is effectively constant. The expression becomes

[math]\displaystyle{ \beta =\mathrm{\frac{[ML] } {[M] [L] }}. }[/math]

Following this simplification a general definition can be given, for the general equilibrium

[math]\displaystyle{ p\mathrm M + q\mathrm L \leftrightharpoons \mathrm M_p \mathrm L_q }[/math]

[math]\displaystyle{ \beta_{pq...}=\frac{[\mathrm{M}_p\mathrm{L}_q...] } {[\mathrm{M}]^p [\mathrm{L}]^q ... } }[/math]

The definition can easily be extended to include any number of reagents. The reagents need not always be a metal and a ligand but can be any species which form a complex. Stability constants defined in this way, are association constants. This can lead to some confusion as pK_a values are dissociation constants. In general purpose computer programs it is customary to define all constants as association constants. The relationship between the two types of constant is given in association and dissociation constants.

Stepwise and cumulative constants

A cumulative or overall constant, given the symbol β, is the constant for the formation of a complex from reagents. For example, the cumulative constant for the formation of ML₂ is given by

[math]\ce{ {M} + 2L <=> ML2 }[/math];     [math]\displaystyle{ \beta_{1,2}=\mathrm{\frac{[ML_2]}{[M][L]^2}} }[/math]

The stepwise constants, K₁ and K₂ refer to the formation of the complexes one step at a time.

[math]\ce{ {M} + L <=> ML }[/math];     [math]\displaystyle{ K_{1}=\mathrm{\frac{[ML]}{[M][L]}} }[/math]

[math]\ce{ {ML} + L <=> ML2 }[/math];     [math]\displaystyle{ K_{2}=\mathrm{\frac{[ML_2]}{[ML][L]}} }[/math]

It follows that

[math]\displaystyle{ \beta_{1,2}=K_1 K_2\, }[/math]

A cumulative constant can always be expressed as the product of stepwise constants. Conversely, any stepwise constant can be expressed as a quotient of two or more overall constants. There is no agreed notation for stepwise constants, though a symbol such as KLML is sometimes found in the literature. It is good practice to specify each stability constant explicitly, as illustrated above.

Hydrolysis products

The formation of a hydroxo complex is a typical example of a hydrolysis reaction. A hydrolysis reaction is one in which a substrate reacts with water, splitting a water molecule into hydroxide and hydrogen ions. In this case the hydroxide ion then forms a complex with the substrate.

[math]\displaystyle{ \mathrm{M + OH} \leftrightharpoons \mathrm{M(OH)} }[/math];      [math]\displaystyle{ K =\mathrm{\frac{[M(OH)] } {[M] [OH] }} }[/math]

In water the concentration of hydroxide is related to the concentration of hydrogen ions by the self-ionization constant, K_w.

[math]\displaystyle{ K_w = \mathrm{[H]}^ + \mathrm{[OH]}^{-1} }[/math]

The expression for hydroxide concentration is substituted into the formation constant expression

[math]\displaystyle{ K=\frac{[\mathrm{M}(\mathrm{OH})] } {[\mathrm{M}] K_\mathrm{w} [\mathrm{H}]^{-1} } }[/math]

[math]\displaystyle{ \beta^*_{1,-1}= K K_\mathrm{w} =\frac{[\mathrm{M}(\mathrm{OH})] } {[\mathrm{M}] [\mathrm{H}]^{-1} } }[/math]

In general, for the reaction

[math]\displaystyle{ \mathrm{M} + n\mathrm{OH} \leftrightharpoons \mathrm{M(OH})_n }[/math]      [math]\displaystyle{ \log \beta^*_{1,-n} \approx \log K - 14n }[/math]

In the older literature the value of log K is usually cited for an hydrolysis constant. The log β^* value is usually cited for an hydrolysed complex with the generic chemical formula M_pL_q(OH)_r.

Acid–base complexes

A Lewis acid, A, and a Lewis base, B, can be considered to form a complex AB.

[math]\displaystyle{ \mathrm A + \mathrm B \leftrightharpoons \mathrm {AB} }[/math]    [math]\displaystyle{ , K =\mathrm{\frac{[AB] } {[A] [B] }} }[/math]

There are three major theories relating to the strength of Lewis acids and bases and the interactions between them.

1. Hard and soft acid–base theory (HSAB). This is used mainly for qualitative purposes.
2. Drago and Wayland proposed a two-parameter equation which predicts the standard enthalpy of formation of a very large number of adducts quite accurately. −ΔH^⊖ (A − B) = E_AE_B + C_AC_B. Values of the E and C parameters are available.
3. Guttmann donor numbers: for bases the number is derived from the enthalpy of reaction of the base with antimony pentachloride in 1,2-Dichloroethane as solvent. For acids, an acceptor number is derived from the enthalpy of reaction of the acid with triphenylphosphine oxide.

For more details see: acid–base reaction, acid catalysis, Extraction

Thermodynamics

The thermodynamics of metal ion complex formation provides much significant information. In particular it is useful in distinguishing between enthalpic and entropic effects. Enthalpic effects depend on bond strengths and entropic effects have to do with changes in the order/disorder of the solution as a whole. The chelate effect, below, is best explained in terms of thermodynamics.

An equilibrium constant is related to the standard Gibbs free energy change for the reaction

[math]\displaystyle{ \Delta G^ \theta = -2.303 RT log \beta }[/math]

R is the gas constant and T is the absolute temperature. At 25 °C, ΔG^⊖ = (−5.708 kJ mol⁻¹) ⋅ log β. Free energy is made up of an enthalpy term and an entropy term.

[math]\displaystyle{ \Delta G^ \theta = \Delta H^ \theta -T\Delta S^ \theta }[/math]

The standard enthalpy change can be determined by calorimetry or by using the Van 't Hoff equation, though the calorimetric method is preferable. When both the standard enthalpy change and stability constant have been determined, the standard entropy change is easily calculated from the equation above.

The fact that stepwise formation constants of complexes of the type ML_n decrease in magnitude as n increases may be partly explained in terms of the entropy factor. Take the case of the formation of octahedral complexes.

[math]\displaystyle{ \mathrm{M(H_2 O)}_m \mathrm {L_{n-1}}+ \mathrm{ L} \leftrightharpoons \mathrm{M(H_2 O)}_{m-1} \mathrm {L_{n}} }[/math]

For the first step m = 6, n = 1 and the ligand can go into one of 6 sites. For the second step m = 5 and the second ligand can go into one of only 5 sites. This means that there is more randomness in the first step than the second one; ΔS^⊖ is more positive, so ΔG^⊖ is more negative and [math]\displaystyle{ K_1 \gt K_2 }[/math]. The ratio of the stepwise stability constants can be calculated on this basis, but experimental ratios are not exactly the same because ΔH^⊖ is not necessarily the same for each step. Exceptions to this rule are discussed below, in #chelate effect and #Geometrical factors.

Ionic strength dependence

The thermodynamic equilibrium constant, K^⊖, for the equilibrium

[math]\displaystyle{ \mathrm {M+L} \leftrightharpoons \mathrm{ML} }[/math]

can be defined as

[math]\displaystyle{ K^{\ominus} =\mathrm{\frac{\{ML\}} {\{M\}\{L\}} } }[/math]

where {ML} is the activity of the chemical species ML etc. K^⊖ is dimensionless since activity is dimensionless. Activities of the products are placed in the numerator, activities of the reactants are placed in the denominator. See activity coefficient for a derivation of this expression.

Since activity is the product of concentration and activity coefficient (γ) the definition could also be written as

[math]\displaystyle{ K^{\ominus} = \mathrm{\frac{[ML]}{[M][L]}}\times \frac{\gamma_\mathrm{ML}}{\gamma_\mathrm{M}\gamma_\mathrm{L}} =\mathrm{\frac{[ML]}{[M][L]}}\times\Gamma }[/math]

where [ML] represents the concentration of ML and Γ is a quotient of activity coefficients. This expression can be generalized as

[math]\displaystyle{ \beta_{pq...}^\ominus=\frac{[\mathrm{M}_p\mathrm{L}_q...] } {[\mathrm{M}]^p [\mathrm{L}]^q ... }\times \Gamma }[/math]

Dependence of the stability constant for formation of [Cu(glycinate)]⁺ on ionic strength (NaClO₄)

To avoid the complications involved in using activities, stability constants are determined, where possible, in a medium consisting of a solution of a background electrolyte at high ionic strength, that is, under conditions in which Γ can be assumed to be always constant. For example, the medium might be a solution of 0.1 mol dm⁻³ sodium nitrate or 3 mol dm⁻³ sodium perchlorate. When Γ is constant it may be ignored and the general expression in theory, above, is obtained.

All published stability constant values refer to the specific ionic medium used in their determination and different values are obtained with different conditions, as illustrated for the complex CuL (L = glycinate). Furthermore, stability constant values depend on the specific electrolyte used as the value of Γ is different for different electrolytes, even at the same ionic strength. There does not need to be any chemical interaction between the species in equilibrium and the background electrolyte, but such interactions might occur in particular cases. For example, phosphates form weak complexes with alkali metals, so, when determining stability constants involving phosphates, such as ATP, the background electrolyte used will be, for example, a tetralkylammonium salt. Another example involves iron(III) which forms weak complexes with halide and other anions, but not with perchlorate ions.

When published constants refer to an ionic strength other than the one required for a particular application, they may be adjusted by means of specific ion theory (SIT) and other theories.

Temperature dependence

All equilibrium constants vary with temperature according to the Van 't Hoff equation

[math]\displaystyle{ \frac {d (\ln K)} {dT} = \frac{\Delta \mathit{H}_\mathrm{m}^\ominus} {RT^2} }[/math]

Alternatively

[math]\displaystyle{ \frac{d \ln K}{d(1/T)}=-\frac{{\Delta H^\ominus}}{{R}} }[/math]

R is the gas constant and T is the thermodynamic temperature. Thus, for exothermic reactions, where the standard enthalpy change, ΔH^⊖, is negative, K decreases with temperature, but for endothermic reactions, where ΔH^⊖ is positive, K increases with temperature.

Factors affecting the stability constants of complexes

The chelate effect

Cu²⁺ complexes with methylamine (left) end ethylene diamine (right)

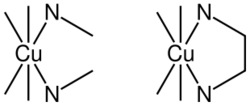
Consider the two equilibria, in aqueous solution, between the copper(II) ion, Cu²⁺ and ethylenediamine (en) on the one hand and methylamine, MeNH₂ on the other.

[math]\displaystyle{ \mathrm{ Cu^{2+} + en \rightleftharpoons [Cu(en)]^{2+}} }[/math]

[math]\displaystyle{ Cu^{2+} + 2 MeNH_2 \rightleftharpoons [Cu(MeNH_2)_2]^{2+} }[/math]

In the first reaction the bidentate ligand ethylene diamine forms a chelate complex with the copper ion. Chelation results in the formation of a five-membered ring. In the second reaction the bidentate ligand is replaced by two monodentate methylamine ligands of approximately the same donor power, meaning that the enthalpy of formation of Cu–N bonds is approximately the same in the two reactions. Under conditions of equal copper concentrations and when the concentration of methylamine is twice the concentration of ethylenediamine, the concentration of the bidentate complex will be greater than the concentration of the complex with 2 monodentate ligands. The effect increases with the number of chelate rings so the concentration of the EDTA complex, which has six chelate rings, is much higher than a corresponding complex with two monodentate nitrogen donor ligands and four monodentate carboxylate ligands. Thus, the phenomenon of the chelate effect is a firmly established empirical fact: under comparable conditions, the concentration of a chelate complex will be higher than the concentration of an analogous complex with monodentate ligands.

The thermodynamic approach to explaining the chelate effect considers the equilibrium constant for the reaction: the larger the equilibrium constant, the higher the concentration of the complex.

[math]\displaystyle{ \mathrm{[Cu(en)] = \beta_{11}[Cu][en]|} }[/math]

[math]\displaystyle{ \mathrm{[Cu(MeNH_2)_2]= \beta _{12}[Cu][MeNH_2]}^2 }[/math]

When the analytical concentration of methylamine is twice that of ethylenediamine and the concentration of copper is the same in both reactions, the concentration [Cu(en)]²⁺ is much higher than the concentration [Cu(MeNH₂)₂]²⁺ because β₁₁ ≫ β₁₂.

The difference between the two stability constants is mainly due to the difference in the standard entropy change, ΔS^⊖. In the reaction with the chelating ligand there are two particles on the left and one on the right, whereas in equation with the monodentate ligand there are three particles on the left and one on the right. This means that less entropy of disorder is lost when the chelate complex is formed than when the complex with monodentate ligands is formed. This is one of the factors contributing to the entropy difference. Other factors include solvation changes and ring formation. Some experimental data to illustrate the effect are shown in the following table.

Equilibrium	log β	ΔG⊖ /kJ mol−1	ΔH⊖ /kJ mol−1	−TΔS⊖ /kJ mol−1
Cd2+ + 4 MeNH2 ⇌ Cd(MeNH2)2+4	6.55	−37.4	−57.3	19.9
Cd2+ + 2 en ⇌ Cd(en)2+2	10.62	−60.67	−56.48	−4.19

An EDTA complex

These data show that the standard enthalpy changes are indeed approximately equal for the two reactions and that the main reason why the chelate complex is so much more stable is that the standard entropy term is much less unfavourable, indeed, it is favourable in this instance. In general it is difficult to account precisely for thermodynamic values in terms of changes in solution at the molecular level, but it is clear that the chelate effect is predominantly an effect of entropy. Other explanations, including that of Schwarzenbach, are discussed in Greenwood and Earnshaw.

diethylenetriamine

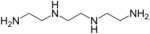
The chelate effect increases as the number of chelate rings increases. For example, the complex [Ni(dien)₂)]²⁺ is more stable than the complex [Ni(en)₃)]²⁺; both complexes are octahedral with six nitrogen atoms around the nickel ion, but dien (diethylenetriamine, 1,4,7-triazaheptane) is a tridentate ligand and en is bidentate. The number of chelate rings is one less than the number of donor atoms in the ligand. EDTA (ethylenediaminetetracetic acid) has six donor atoms so it forms very strong complexes with five chelate rings. Ligands such as DTPA, which have eight donor atoms are used to form complexes with large metal ions such as lanthanide or actinide ions which usually form 8- or 9-coordinate complexes. 5-membered and 6-membered chelate rings give the most stable complexes. 4-membered rings are subject to internal strain because of the small inter-bond angle is the ring. The chelate effect is also reduced with 7- and 8- membered rings, because the larger rings are less rigid, so less entropy is lost in forming them.

Deprotonation of aliphatic –OH groups

thumb|left|125px|2-aminoethanol thumb|125px|Tris Removal of a proton from an aliphatic –OH group is difficult to achieve in aqueous solution because the energy required for this process is rather large. Thus, ionization of aliphatic –OH groups occurs in aqueous solution only in special circumstances. One such circumstance is found with compounds containing the H₂N–C–C–OH substructure. For example, compounds containing the 2-aminoethanol substructure can form metal–chelate complexes with the deprotonated form, H₂N–C–C–O⁻. The chelate effect supplies the extra energy needed to break the O–H bond.

An important example occurs with the molecule tris. This molecule should be used with caution as a buffering agent as it will form chelate complexes with ions such as Fe³⁺ and Cu²⁺.

The macrocyclic effect

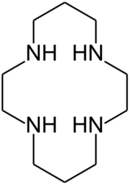
It was found that the stability of the complex of copper(II) with the macrocyclic ligand cyclam (1,4,8,11-tetraazacyclotetradecane) was much greater than expected in comparison to the stability of the complex with the corresponding open-chain amine. This phenomenon was named the macrocyclic effect and it was also interpreted as an entropy effect. However, later studies suggested that both enthalpy and entropy factors were involved.

An important difference between macrocyclic ligands and open-chain (chelating) ligands is that they have selectivity for metal ions, based on the size of the cavity into which the metal ion is inserted when a complex is formed. For example, the crown ether 18-crown-6 forms much stronger complexes with the potassium ion, K⁺ than with the smaller sodium ion, Na⁺.

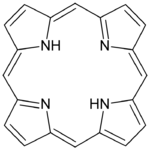
In hemoglobin an iron(II) ion is complexed by a macrocyclic porphyrin ring. The article hemoglobin incorrectly states that oxyhemoglogin contains iron(III). It is now known that the iron(II) in hemoglobin is a low-spin complex, whereas in oxyhemoglobin it is a high-spin complex. The low-spin Fe²⁺ ion fits snugly into the cavity of the porphyrin ring, but high-spin iron(II) is significantly larger and the iron atom is forced out of the plane of the macrocyclic ligand. This effect contributes the ability of hemoglobin to bind oxygen reversibly under biological conditions. In Vitamin B12 a cobalt(II) ion is held in a corrin ring. Chlorophyll is a macrocyclic complex of magnesium(II).

Cyclam	Porphine, the simplest porphyrin.

Structures of common crown ethers: 12-crown-4, 15-crown-5, 18-crown-6, dibenzo-18-crown-6, and an aza-crown ether

Geometrical factors

Successive stepwise formation constants K_n in a series such as ML_n (n = 1, 2, ...) usually decrease as n increases. Exceptions to this rule occur when the geometry of the ML_n complexes is not the same for all members of the series. The classic example is the formation of the diamminesilver(I) complex [Ag(NH₃)₂]⁺ in aqueous solution.

[math]\displaystyle{ \mathrm{Ag^+ + NH_3 \rightleftharpoons [Ag(NH_3)]^+ ; K_1 = \frac{{[Ag(NH_3)]}}{{[Ag][NH_3]}}} }[/math]

[math]\displaystyle{ \mathrm{Ag(NH_3)^+ + NH_3 \rightleftharpoons [Ag(NH_3)_2]^+ ; K_2 = \frac{{[Ag(NH_3)_2]}}{{[Ag(NH_3][NH_3]}}} }[/math]

In this case, K₂ > K₁. The reason for this is that, in aqueous solution, the ion written as Ag⁺ actually exists as the four-coordinate tetrahedral aqua species [Ag(H₂O)₄]⁺. The first step is then a substitution reaction involving the displacement of a bound water molecule by ammonia forming the tetrahedral complex [Ag(NH₃)(H₂O)₃]⁺. In the second step, all the aqua ligands are lost and a linear, two-coordinate product [H₃N–Ag–NH₃]⁺ is formed. Examination of the thermodynamic data shows that the difference in entropy change is the main contributor to the difference in stability constants for the two complexation reactions.

equilibrium	ΔH⊖ /kJ mol−1	ΔS⊖ /J K−1 mol−1
Ag+ + NH3 ⇌ [Ag(NH3)]+	−21.4	8.66
[Ag(NH3)]+ + NH3 ⇌ [Ag(NH3)2]+	−35.2	−61.26

Other examples exist where the change is from octahedral to tetrahedral, as in the formation of [CoCl₄]²⁻ from [Co(H₂O)₆]²⁺.

Classification of metal ions

Ahrland, Chatt and Davies proposed that metal ions could be described as class A if they formed stronger complexes with ligands whose donor atoms are nitrogen, oxygen or fluorine than with ligands whose donor atoms are phosphorus, sulfur or chlorine and class B if the reverse is true. For example, Ni²⁺ forms stronger complexes with amines than with phosphines, but Pd²⁺ forms stronger complexes with phosphines than with amines. Later, Pearson proposed the theory of hard and soft acids and bases (HSAB theory). In this classification, class A metals are hard acids and class B metals are soft acids. Some ions, such as copper(I), are classed as borderline. Hard acids form stronger complexes with hard bases than with soft bases. In general terms hard–hard interactions are predominantly electrostatic in nature whereas soft–soft interactions are predominantly covalent in nature. The HSAB theory, though useful, is only semi-quantitative.

The hardness of a metal ion increases with oxidation state. An example of this effect is given by the fact that Fe²⁺ tends to form stronger complexes with N-donor ligands than with O-donor ligands, but the opposite is true for Fe³⁺.

Effect of ionic radius

The Irving–Williams series refers to high-spin, octahedral, divalent metal ion of the first transition series. It places the stabilities of complexes in the order

Mn < Fe < Co < Ni < Cu > Zn

This order was found to hold for a wide variety of ligands. There are three strands to the explanation of the series.

1. The ionic radius is expected to decrease regularly for Mn²⁺ to Zn²⁺. This would be the normal periodic trend and would account for the general increase in stability.
2. The crystal field stabilisation energy (CFSE) increases from zero for manganese(II) to a maximum at nickel(II). This makes the complexes increasingly stable. CFSE returns to zero for zinc(II).
3. Although the CFSE for copper(II) is less than for nickel(II), octahedral copper(II) complexes are subject to the Jahn–Teller effect which results in a complex having extra stability.

Another example of the effect of ionic radius the steady increase in stability of complexes with a given ligand along the series of trivalent lanthanide ions, an effect of the well-known lanthanide contraction.

Applications

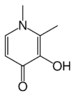
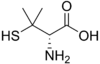
Stability constant values are exploited in a wide variety of applications. Chelation therapy is used in the treatment of various metal-related illnesses, such as iron overload in β-thalassemia sufferers who have been given blood transfusions. The ideal ligand binds to the target metal ion and not to others, but this degree of selectivity is very hard to achieve. The synthetic drug deferiprone achieves selectivity by having two oxygen donor atoms so that it binds to Fe³⁺ in preference to any of the other divalent ions that are present in the human body, such as Mg²⁺, Ca²⁺ and Zn²⁺. Treatment of poisoning by ions such as Pb²⁺ and Cd²⁺ is much more difficult since these are both divalent ions and selectivity is harder to accomplish. Excess copper in Wilson's disease can be removed by penicillamine or Triethylene tetramine (TETA). DTPA has been approved by the U.S. Food and Drug Administration for treatment of plutonium poisoning.

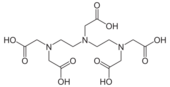
DTPA is also used as a complexing agent for gadolinium in MRI contrast enhancement. The requirement in this case is that the complex be very strong, as Gd³⁺ is very toxic. The large stability constant of the octadentate ligand ensures that the concentration of free Gd³⁺ is almost negligible, certainly well below toxicity threshold. In addition the ligand occupies only 8 of the 9 coordination sites on the gadolinium ion. The ninth site is occupied by a water molecule which exchanges rapidly with the fluid surrounding it and it is this mechanism that makes the paramagnetic complex into a contrast reagent.

EDTA forms such strong complexes with most divalent cations that it finds many uses. For example, it is often present in washing powder to act as a water softener by sequestering calcium and magnesium ions.

The selectivity of macrocyclic ligands can be used as a basis for the construction of an ion selective electrode. For example, potassium selective electrodes are available that make use of the naturally occurring macrocyclic antibiotic valinomycin.

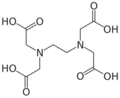Deferiprone	Penicillamine	triethylenetetramine, TETA	Ethylenediaminetetraacetic acid, EDTA
Diethylenetriaminepentaacetic acid, DTPA	Valinomycin	Tri-n-butyl phosphate

An ion-exchange resin such as chelex 100, which contains chelating ligands bound to a polymer, can be used in water softeners and in chromatographic separation techniques. In solvent extraction the formation of electrically neutral complexes allows cations to be extracted into organic solvents. For example, in nuclear fuel reprocessing uranium(VI) and plutonium(VI) are extracted into kerosene as the complexes [MO₂(TBP)₂(NO₃)₂] (TBP = tri-n-butyl phosphate). In phase-transfer catalysis, a substance which is insoluble in an organic solvent can be made soluble by addition of a suitable ligand. For example, potassium permanganate oxidations can be achieved by adding a catalytic quantity of a crown ether and a small amount of organic solvent to the aqueous reaction mixture, so that the oxidation reaction occurs in the organic phase.

In all these examples, the ligand is chosen on the basis of the stability constants of the complexes formed. For example, TBP is used in nuclear fuel reprocessing because (among other reasons) it forms a complex strong enough for solvent extraction to take place, but weak enough that the complex can be destroyed by nitric acid to recover the uranyl cation as nitrato complexes, such as [UO₂(NO₃)₄]²⁻ back in the aqueous phase.

Supramolecular complexes

Supramolecular complexes are held together by hydrogen bonding, hydrophobic forces, van der Waals forces, π-π interactions, and electrostatic effects, all of which can be described as noncovalent bonding. Applications include molecular recognition, host–guest chemistry and anion sensors.

A typical application in molecular recognition involved the determination of formation constants for complexes formed between a tripodal substituted urea molecule and various saccharides. The study was carried out using a non-aqueous solvent and NMR chemical shift measurements. The object was to examine the selectivity with respect to the saccharides.

An example of the use of supramolecular complexes in the development of chemosensors is provided by the use of transition-metal ensembles to sense for ATP.

Anion complexation can be achieved by encapsulating the anion in a suitable cage. Selectivity can be engineered by designing the shape of the cage. For example, dicarboxylate anions could be encapsulated in the ellipsoidal cavity in a large macrocyclic structure containing two metal ions.

Experimental methods

The method developed by Bjerrum is still the main method in use today, though the precision of the measurements has greatly increased. Most commonly, a solution containing the metal ion and the ligand in a medium of high ionic strength is first acidified to the point where the ligand is fully protonated. This solution is then titrated, often by means of a computer-controlled auto-titrator, with a solution of CO₂-free base. The concentration, or activity, of the hydrogen ion is monitored by means of a glass electrode. The data set used for the calculation has three components: a statement defining the nature of the chemical species that will be present, called the model of the system, details concerning the concentrations of the reagents used in the titration, and finally the experimental measurements in the form of titre and pH (or emf) pairs.

Other ion-selective electrodes (ISE) may be used. For example, a fluoride electrode may be used with the determination of stability complexes of fluoro-complexes of a metal ion.

It is not always possible to use an ISE. If that is the case, the titration can be monitored by other types of measurement. Ultraviolet–visible spectroscopy, fluorescence spectroscopy and NMR spectroscopy are the most commonly used alternatives. Current practice is to take absorbance or fluorescence measurements at a range of wavelengths and to fit these data simultaneously. Various NMR chemical shifts can also be fitted together.

The chemical model will include values of the protonation constants of the ligand, which will have been determined in separate experiments, a value for log K_w and estimates of the unknown stability constants of the complexes formed. These estimates are necessary because the calculation uses a non-linear least-squares algorithm. The estimates are usually obtained by reference to a chemically similar system. The stability constant databases can be very useful in finding published stability constant values for related complexes.

In some simple cases the calculations can be done in a spreadsheet. Otherwise, the calculations are performed with the aid of a general-purpose computer programs. The most frequently used programs are:

• Potentiometric and/or spectrophotometric data: PSEQUAD
• Potentiometric data: HYPERQUAD, BEST, ReactLab pH PRO
• Spectrophotometric data: HypSpec, SQUAD, SPECFIT, ReactLab EQUILIBRIA.
• NMR data HypNMR, WINEQNMR2

In biochemistry, formation constants of adducts may be obtained from Isothermal titration calorimetry (ITC) measurements. This technique yields both the stability constant and the standard enthalpy change for the equilibrium. It is mostly limited, by availability of software, to complexes of 1:1 stoichiometry.

Critically evaluated data

The following references are for critical reviews of published stability constants for various classes of ligands. All these reviews are published by IUPAC and the full text is available, free of charge, in pdf format.

• ethylenediamine (en)
• Nitrilotriacetic acid (NTA)
• aminopolycarboxylic acids (complexones)
• Alpha hydroxy acids and other hydroxycarboxylic acids

• crown ethers

• phosphonic acids

• imidazoles and histamines

• amino acids with polar side-chains

• nucleotides

• acetylacetone

• general

• Chemical speciation of environmentally significant heavy metals with inorganic ligands. Part 1: The Hg²⁺–Cl⁻, OH⁻, CO2−3, SO2−4, and PO3−4 systems.
• Chemical speciation of environmentally significant metals with inorganic ligands Part 2: The Cu²⁺–OH⁻, Cl⁻, CO2−3, SO2−4, and PO3−4 aqueous systems
• Chemical speciation of environmentally significant metals with inorganic ligands Part 3: The Pb²⁺–OH⁻, Cl⁻, CO2−3, SO2−4, and PO3−4 systems
• Chemical speciation of environmentally significant metals with inorganic ligands. Part 4: The Cd²⁺–OH⁻, Cl⁻, CO2−3, SO2−4, and PO3−4 systems

Databases

• The Ki Database is a public domain database of published binding affinities (Ki) of drugs and chemical compounds for receptors, neurotransmitter transporters, ion channels, and enzymes.
• BindingDB is a public domain database of measured binding affinities, focusing chiefly on the interactions of protein considered to be drug-targets with small, drug-like molecules

Further reading

Sigel, Roland K. O.; Skilandat, Miriam; Sigel, Astrid; Operschall, Bert P.; Sigel, Helmut (2013). "Chapter 8. Complex formation of cadmium with sugar residues, nucleobases, phosphates, nucleotides and nucleic acids". in Sigel, Astrid; Sigel, Helmut; Sigel, Roland K. O.. Cadmium: From Toxicology to Essentiality. Metal Ions in Life Sciences. 11. Springer. pp. 191–274. doi:10.1007/978-94-007-5179-8_8. http://www.zora.uzh.ch/id/eprint/79639/2/MILS-11_ch8_sigel_final_re.pdf. 

Sóvágó, Imre; Várnagy, Katalin (2013). "Chapter 9. Cadmium(II) complexes of amino acids and peptides". in Sigel, Astrid; Sigel, Helmut; Sigel, Roland K. O.. Cadmium: From Toxicology to Essentiality. Metal Ions in Life Sciences. 11. Springer. pp. 275–302. doi:10.1007/978-94-007-5179-8_9. 

Yatsimirsky, Konstantin Borisovich; Vasilyev, Vladimir Pavlovich (1960). Instability Constants of Complex Compounds. OUP. 

External links

• Stability constants website: Contains information on computer programs, applications, databases and hardware for experimental titrations.