Erdős–Anning theorem

Short description: On sets of points with integer distances

The integer number line, a set of infinitely many points with integer distances. According to the Erdős–Anning theorem, any such set lies on a line.

The Erdős–Anning theorem states that, whenever an infinite number of points in the plane all have integer distances, the points lie on a straight line. The same result holds in higher dimensional Euclidean spaces. The theorem cannot be strengthened to give a finite bound on the number of points: there exist arbitrarily large finite sets of points that are not on a line and have integer distances.

The theorem is named after Paul Erdős and Norman H. Anning, who published a proof of it in 1945. Erdős later supplied a simpler proof, which can also be used to check whether a point set forms an Erdős–Diophantine graph, an inextensible system of integer points with integer distances. The Erdős–Anning theorem inspired the Erdős–Ulam problem on the existence of dense point sets with rational distances.

Rationality versus integrality

The integer multiples of the angle of a 3–4–5 right triangle. All pairwise distances among the even multiples (every other point from this set) are rational numbers. Scaling any finite subset of these points by the least common denominator of their distances produces an arbitrarily large finite set of points at integer distances from each other.

Although there can be no infinite non-collinear set of points with integer distances, there are infinite non-collinear sets of points whose distances are rational numbers. For instance, the subset of points on a unit circle obtained as the even multiples of one of the acute angles of an integer-sided right triangle (such as the triangle with side lengths 3, 4, and 5) has this property. This construction forms a dense set in the circle. The (still unsolved) Erdős–Ulam problem asks whether there can exist a set of points at rational distances from each other that forms a dense set for the whole Euclidean plane. According to Erdős, Stanisław Ulam was inspired to ask this question after hearing from Erdős about the Erdős–Anning theorem.

For any finite set S of points at rational distances from each other, it is possible to find a similar set of points at integer distances from each other, by expanding S by a factor of the least common denominator of the distances in S. By expanding in this way a finite subset of the unit circle construction, one can construct arbitrarily large finite sets of non-collinear points with integer distances from each other. However, including more points into S may cause the expansion factor to increase, so this construction does not allow infinite sets of points at rational distances to be transformed into infinite sets of points at integer distances.

Proof

Illustration for a proof of the Erdős–Anning theorem. Given three non-collinear points A, B, C with integer distances from each other (here, the vertices of a 3–4–5 right triangle), the points whose distances to A and B differ by an integer lie on a system of hyperbolas and degenerate hyperbolas (blue), and symmetrically the points whose distances to B and C differ by an integer lie on another system of hyperbolas (red). Any point with integer distance to all three of A, B, C lies on a crossing of a blue and a red curve. There are finitely many crossings, so finitely many additional points in the set. Each branch of a hyperbola is labeled by the integer difference of distances that is invariant for the points on that branch.

Shortly after the original publication of the Erdős–Anning theorem, Erdős provided the following simpler proof.

The proof assumes a given set of points with integer distances, not all on a line. It then proves that this set must be finite, using a system of curves for which each point of the given set lies on a crossing of two of the curves. In more detail, it consists of the following steps:

• Arbitrarily choose a triangle [math]\displaystyle{ ABC }[/math] formed by three of the given points. The figure shows an example for which these three chosen points form a right triangle (yellow) with edge lengths 3, 4, and 5.
• Let [math]\displaystyle{ d }[/math] denote the Euclidean distance function. For any given point [math]\displaystyle{ X }[/math], the integer [math]\displaystyle{ |d(A,X)-d(B,X)| }[/math] is at most [math]\displaystyle{ d(A,B) }[/math], by the triangle inequality. Thus, [math]\displaystyle{ X }[/math] lies on one of [math]\displaystyle{ d(A,B) }[/math] hyperbolas, defined by equations of the form [math]\displaystyle{ |d(A,X)-d(B,X)|=i }[/math] with [math]\displaystyle{ 0\le i\lt d(A,B) }[/math]. These are shown in blue in the figure. For [math]\displaystyle{ i=d(A,B) }[/math] this equation instead defines two rays extending in opposite directions on the line through [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math] (also shown in blue); this pair of rays can be treated as a degenerate hyperbola for the purposes of the proof.
• By a symmetric argument, [math]\displaystyle{ X }[/math] must also lie on one of [math]\displaystyle{ d(B,C)+1 }[/math] hyperbolas or degenerate hyperbolas defined by equations of the form [math]\displaystyle{ |d(B,X)-d(C,X)|=j }[/math] with [math]\displaystyle{ 0\le j\le d(B,C) }[/math]. These are shown in red in the figure.
• The blue and red hyperbolas containing [math]\displaystyle{ X }[/math] cannot coincide, because they have different pairs of foci. Thus, [math]\displaystyle{ X }[/math] must be a point where they intersect. Each pair of a blue and red hyperbola have at most four intersection points, by Bézout's theorem.
• Because each given point must be one of these intersection points, the number of given points is at most the product of the number of pairs of hyperbolas and the number of intersections per pair. This is at most [math]\displaystyle{ 4\bigl(d(A,B)+1\bigr)\bigl(d(B,C)+1\bigr) }[/math] points, a finite number.

The same proof shows that, when the diameter of a set of points with integer distances is [math]\displaystyle{ \delta }[/math], there are at most [math]\displaystyle{ 4(\delta+1)^2 }[/math] points. The quadratic dependence of this bound on [math]\displaystyle{ \delta }[/math] can be improved, using a similar proof but with a more careful choice of the pairs of points used to define families of hyperbolas: every point set with integer distances and diameter [math]\displaystyle{ \delta }[/math] has size [math]\displaystyle{ O(\delta) }[/math], where the [math]\displaystyle{ O(\,) }[/math] uses big O notation. However, it is not possible to replace [math]\displaystyle{ \delta }[/math] by the minimum distance between the points: there exist arbitrarily large non-collinear point sets with integer distances and with minimum distance two.

Maximal point sets with integral distances

Five-vertex Erdős–Diophantine graph

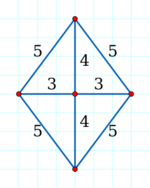
An alternative way of stating the theorem is that a non-collinear set of points in the plane with integer distances can only be extended by adding finitely many additional points, before no more points can be added. A set of points with both integer coordinates and integer distances, to which no more can be added while preserving both properties, forms an Erdős–Diophantine graph.

The proof of the Erdős–Anning theorem can be used in an algorithm to check whether a given set of integer points with integer distances forms an Erdős–Diophantine graph: merely find all of the crossing points of the hyperbolas used in the proof, and check whether any of the resulting points also have integer coordinates and integer distances from the given set.

Higher dimensions

As Anning and Erdős wrote in their original paper on this theorem, "by a similar argument we can show that we cannot have infinitely many points in [math]\displaystyle{ n }[/math]-dimensional space not all on a line, with all the distances being integral."