Practical number

Short description: Number such that it and all smaller numbers may be represented as sums of its distinct divisors

Demonstration of the practicality of the number 12

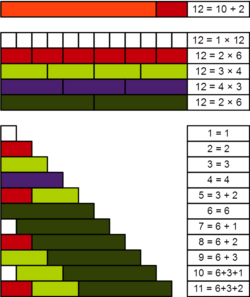
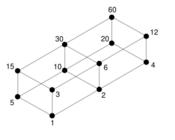
In number theory, a practical number or panarithmic number is a positive integer [math]\displaystyle{ n }[/math] such that all smaller positive integers can be represented as sums of distinct divisors of [math]\displaystyle{ n }[/math]. For example, 12 is a practical number because all the numbers from 1 to 11 can be expressed as sums of its divisors 1, 2, 3, 4, and 6: as well as these divisors themselves, we have 5 = 3 + 2, 7 = 6 + 1, 8 = 6 + 2, 9 = 6 + 3, 10 = 6 + 3 + 1, and 11 = 6 + 3 + 2.

The sequence of practical numbers (sequence A005153 in the OEIS) begins

1, 2, 4, 6, 8, 12, 16, 18, 20, 24, 28, 30, 32, 36, 40, 42, 48, 54, 56, 60, 64, 66, 72, 78, 80, 84, 88, 90, 96, 100, 104, 108, 112, 120, 126, 128, 132, 140, 144, 150....

Practical numbers were used by Fibonacci in his Liber Abaci (1202) in connection with the problem of representing rational numbers as Egyptian fractions. Fibonacci does not formally define practical numbers, but he gives a table of Egyptian fraction expansions for fractions with practical denominators.

The name "practical number" is due to (Srinivasan 1948). He noted that "the subdivisions of money, weights, and measures involve numbers like 4, 12, 16, 20 and 28 which are usually supposed to be so inconvenient as to deserve replacement by powers of 10." His partial classification of these numbers was completed by (Stewart 1954) and (Sierpiński 1955). This characterization makes it possible to determine whether a number is practical by examining its prime factorization. Every even perfect number and every power of two is also a practical number.

Practical numbers have also been shown to be analogous with prime numbers in many of their properties.

Characterization of practical numbers

The original characterisation by (Srinivasan 1948) stated that a practical number cannot be a deficient number, that is one of which the sum of all divisors (including 1 and itself) is less than twice the number unless the deficiency is one. If the ordered set of all divisors of the practical number [math]\displaystyle{ n }[/math] is [math]\displaystyle{ {d_1, d_2,..., d_j} }[/math] with [math]\displaystyle{ d_1=1 }[/math] and [math]\displaystyle{ d_j=n }[/math], then Srinivasan's statement can be expressed by the inequality [math]\displaystyle{ 2n\leq1+\sum_{i=1}^j d_i. }[/math] In other words, the ordered sequence of all divisors [math]\displaystyle{ {d_1\lt d_2\lt ...\lt d_j} }[/math] of a practical number has to be a complete sub-sequence.

This partial characterization was extended and completed by (Stewart 1954) and (Sierpiński 1955) who showed that it is straightforward to determine whether a number is practical from its prime factorization. A positive integer greater than one with prime factorization [math]\displaystyle{ n=p_1^{\alpha_1}...p_k^{\alpha_k} }[/math] (with the primes in sorted order [math]\displaystyle{ p_1\lt p_2\lt \dots\lt p_k }[/math]) is practical if and only if each of its prime factors [math]\displaystyle{ p_i }[/math] is small enough for [math]\displaystyle{ p_i-1 }[/math] to have a representation as a sum of smaller divisors. For this to be true, the first prime [math]\displaystyle{ p_1 }[/math] must equal 2 and, for every i from 2 to k, each successive prime [math]\displaystyle{ p_i }[/math] must obey the inequality

[math]\displaystyle{ p_i\leq1+\sigma(p_1^{\alpha_1}p_2^{\alpha_2}\dots p_{i-1}^{\alpha_{i-1}})=1+\sigma(p_1^{\alpha_1})\sigma(p_2^{\alpha_2})\dots \sigma(p_{i-1}^{\alpha_{i-1}})=1+\prod_{j=1}^{i-1}\frac{p_j^{\alpha_j+1}-1}{p_j-1}, }[/math]

where [math]\displaystyle{ \sigma(x) }[/math] denotes the sum of the divisors of x. For example, 2 × 3² × 29 × 823 = 429606 is practical, because the inequality above holds for each of its prime factors: 3 ≤ σ(2) + 1 = 4, 29 ≤ σ(2 × 3²) + 1 = 40, and 823 ≤ σ(2 × 3² × 29) + 1 = 1171.

The condition stated above is necessary and sufficient for a number to be practical. In one direction, this condition is necessary in order to be able to represent [math]\displaystyle{ p_i-1 }[/math] as a sum of divisors of [math]\displaystyle{ n }[/math], because if the inequality failed to be true then even adding together all the smaller divisors would give a sum too small to reach [math]\displaystyle{ p_i-1 }[/math]. In the other direction, the condition is sufficient, as can be shown by induction. More strongly, if the factorization of [math]\displaystyle{ n }[/math] satisfies the condition above, then any [math]\displaystyle{ m \le \sigma(n) }[/math] can be represented as a sum of divisors of [math]\displaystyle{ n }[/math], by the following sequence of steps:

• By induction on [math]\displaystyle{ j\in[1,\alpha_k] }[/math], it can be shown that [math]\displaystyle{ p_k^j\leq 1+\sigma(n/p_k^{\alpha_k-(j-1)}) }[/math]. Hence [math]\displaystyle{ p_k^{\alpha_k}\leq 1+\sigma(n/p_k) }[/math].
• Since the internals [math]\displaystyle{ [q p_k^{\alpha_k}, q p_k^{\alpha_k}+\sigma(n/p_k)] }[/math] cover [math]\displaystyle{ [1,\sigma(n)] }[/math] for [math]\displaystyle{ 1\leq q\leq \sigma(n/p_k^{\alpha_k}) }[/math], there are such a [math]\displaystyle{ q }[/math] and some [math]\displaystyle{ r\in[0,\sigma(n/p_k)] }[/math] such that [math]\displaystyle{ m=q p_k^{\alpha_k}+r }[/math].
• Since [math]\displaystyle{ q\le\sigma(n/p_k^{\alpha_k}) }[/math] and [math]\displaystyle{ n/p_k^{\alpha_k} }[/math] can be shown by induction to be practical, we can find a representation of q as a sum of divisors of [math]\displaystyle{ n/p_k^{\alpha_k} }[/math].
• Since [math]\displaystyle{ r\le \sigma(n/p_k) }[/math], and since [math]\displaystyle{ n/p_k }[/math] can be shown by induction to be practical, we can find a representation of r as a sum of divisors of [math]\displaystyle{ n/p_k }[/math].
• The divisors representing r, together with [math]\displaystyle{ p_k^{\alpha_k} }[/math] times each of the divisors representing q, together form a representation of m as a sum of divisors of [math]\displaystyle{ n }[/math].

Properties

• The only odd practical number is 1, because if [math]\displaystyle{ n }[/math] is an odd number greater than 2, then 2 cannot be expressed as the sum of distinct divisors of [math]\displaystyle{ n }[/math]. More strongly, (Srinivasan 1948) observes that other than 1 and 2, every practical number is divisible by 4 or 6 (or both).
• The product of two practical numbers is also a practical number. Equivalently, the set of all practical numbers is closed under multiplication. More strongly, the least common multiple of any two practical numbers is also a practical number.
• From the above characterization by Stewart and Sierpiński it can be seen that if [math]\displaystyle{ n }[/math] is a practical number and [math]\displaystyle{ d }[/math] is one of its divisors then [math]\displaystyle{ n\cdot d }[/math] must also be a practical number.
• In the set of all practical numbers there is a primitive set of practical numbers. A primitive practical number is either practical and squarefree or practical and when divided by any of its prime factors whose factorization exponent is greater than 1 is no longer practical. The sequence of primitive practical numbers (sequence A267124 in the OEIS) begins

1, 2, 6, 20, 28, 30, 42, 66, 78, 88, 104, 140, 204, 210, 220, 228, 260, 272, 276, 304, 306, 308, 330, 340, 342, 348, 364, 368, 380, 390, 414, 460 ...

• Every positive integer has a practical multiple. For instance, for every integer [math]\displaystyle{ n }[/math], its multiple [math]\displaystyle{ 2^{\lfloor\log_2 n\rfloor}n }[/math] is practical.

Relation to other classes of numbers

Several other notable sets of integers consist only of practical numbers:

• From the above properties with [math]\displaystyle{ n }[/math] a practical number and [math]\displaystyle{ d }[/math] one of its divisors (that is, [math]\displaystyle{ d|n }[/math]) then [math]\displaystyle{ n\cdot d }[/math] must also be a practical number therefore six times every power of 3 must be a practical number as well as six times every power of 2.
• Every power of two is a practical number. Powers of two trivially satisfy the characterization of practical numbers in terms of their prime factorizations: the only prime in their factorizations, p₁, equals two as required.
• Every even perfect number is also a practical number. This follows from Leonhard Euler's result that an even perfect number must have the form [math]\displaystyle{ 2^{k-1}(2^k-1) }[/math]. The odd part of this factorization equals the sum of the divisors of the even part, so every odd prime factor of such a number must be at most the sum of the divisors of the even part of the number. Therefore, this number must satisfy the characterization of practical numbers. A similar argument can be used to show that an even perfect number when divided by 2 is no longer practical. Therefore, every even perfect number is also a primitive practical number.
• Every primorial (the product of the first [math]\displaystyle{ i }[/math] primes, for some [math]\displaystyle{ i }[/math]) is practical. For the first two primorials, two and six, this is clear. Each successive primorial is formed by multiplying a prime number [math]\displaystyle{ p_i }[/math] by a smaller primorial that is divisible by both two and the next smaller prime, [math]\displaystyle{ p_{i-1} }[/math]. By Bertrand's postulate, [math]\displaystyle{ p_i\lt 2p_{i-1} }[/math], so each successive prime factor in the primorial is less than one of the divisors of the previous primorial. By induction, it follows that every primorial satisfies the characterization of practical numbers. Because a primorial is, by definition, squarefree it is also a primitive practical number.
• Generalizing the primorials, any number that is the product of nonzero powers of the first [math]\displaystyle{ k }[/math] primes must also be practical. This includes Ramanujan's highly composite numbers (numbers with more divisors than any smaller positive integer) as well as the factorial numbers.

Practical numbers and Egyptian fractions

If [math]\displaystyle{ n }[/math] is practical, then any rational number of the form [math]\displaystyle{ m/n }[/math] with [math]\displaystyle{ m\lt n }[/math] may be represented as a sum [math]\displaystyle{ \sum d_i/n }[/math] where each [math]\displaystyle{ d_i }[/math] is a distinct divisor of [math]\displaystyle{ n }[/math]. Each term in this sum simplifies to a unit fraction, so such a sum provides a representation of [math]\displaystyle{ m/n }[/math] as an Egyptian fraction. For instance, [math]\displaystyle{ \frac{13}{20}=\frac{10}{20}+\frac{2}{20}+\frac{1}{20}=\frac12+\frac1{10}+\frac1{20}. }[/math]

Fibonacci, in his 1202 book Liber Abaci lists several methods for finding Egyptian fraction representations of a rational number. Of these, the first is to test whether the number is itself already a unit fraction, but the second is to search for a representation of the numerator as a sum of divisors of the denominator, as described above. This method is only guaranteed to succeed for denominators that are practical. Fibonacci provides tables of these representations for fractions having as denominators the practical numbers 6, 8, 12, 20, 24, 60, and 100.

(Vose 1985) showed that every rational number [math]\displaystyle{ x/y }[/math] has an Egyptian fraction representation with [math]\displaystyle{ O(\sqrt{\log y}) }[/math] terms. The proof involves finding a sequence of practical numbers [math]\displaystyle{ n_i }[/math] with the property that every number less than [math]\displaystyle{ n_i }[/math] may be written as a sum of [math]\displaystyle{ O(\sqrt{\log n_{i-1}}) }[/math] distinct divisors of [math]\displaystyle{ n_i }[/math]. Then, [math]\displaystyle{ i }[/math] is chosen so that [math]\displaystyle{ n_{i-1}\lt y\lt n_i }[/math], and [math]\displaystyle{ xn_i }[/math] is divided by [math]\displaystyle{ y }[/math] giving quotient [math]\displaystyle{ q }[/math] and remainder [math]\displaystyle{ r }[/math]. It follows from these choices that [math]\displaystyle{ \frac{x}{y}=\frac{q}{n_i}+\frac{r}{yn_i} }[/math]. Expanding both numerators on the right hand side of this formula into sums of divisors of [math]\displaystyle{ n_i }[/math] results in the desired Egyptian fraction representation. (Tenenbaum Yokota) use a similar technique involving a different sequence of practical numbers to show that every rational number [math]\displaystyle{ x/y }[/math] has an Egyptian fraction representation in which the largest denominator is [math]\displaystyle{ O(y\log^2 y/\log\log y) }[/math].

According to a September 2015 conjecture by Zhi-Wei Sun, every positive rational number has an Egyptian fraction representation in which every denominator is a practical number. The conjecture was proved by David Eppstein (2021).

Analogies with prime numbers

One reason for interest in practical numbers is that many of their properties are similar to properties of the prime numbers. Indeed, theorems analogous to Goldbach's conjecture and the twin prime conjecture are known for practical numbers: every positive even integer is the sum of two practical numbers, and there exist infinitely many triples of practical numbers [math]\displaystyle{ (x-2,x,x+2) }[/math]. Melfi also showed that there are infinitely many practical Fibonacci numbers (sequence A124105 in the OEIS); the analogous question of the existence of infinitely many Fibonacci primes is open. (Hausman Shapiro) showed that there always exists a practical number in the interval [math]\displaystyle{ [x^2,(x+1)^2)] }[/math] for any positive real [math]\displaystyle{ x }[/math], a result analogous to Legendre's conjecture for primes. Moreover, for all sufficiently large [math]\displaystyle{ x }[/math], the interval [math]\displaystyle{ [x-x^{0.4872},x] }[/math] contains many practical numbers.

Let [math]\displaystyle{ p(x) }[/math] count how many practical numbers are at most [math]\displaystyle{ x }[/math]. (Margenstern 1991) conjectured that [math]\displaystyle{ p(x) }[/math] is asymptotic to [math]\displaystyle{ cx/\log x }[/math] for some constant [math]\displaystyle{ c }[/math], a formula which resembles the prime number theorem, strengthening the earlier claim of (Erdős Loxton) that the practical numbers have density zero in the integers. Improving on an estimate of (Tenenbaum 1986), (Saias 1997) found that [math]\displaystyle{ p(x) }[/math] has order of magnitude [math]\displaystyle{ x/\log x }[/math]. (Weingartner 2015) proved Margenstern's conjecture. We have [math]\displaystyle{ p(x) = \frac{c x}{\log x}\left(1 + O\!\left(\frac{1}{\log x}\right)\right), }[/math] where [math]\displaystyle{ c=1.33607... }[/math] Thus the practical numbers are about 33.6% more numerous than the prime numbers. The exact value of the constant factor [math]\displaystyle{ c }[/math] is given by [math]\displaystyle{ c= \frac{1}{1-e^{-\gamma}} \sum_{n \ \text{practical}} \frac{1}{n} \Biggl( \sum_{p\le \sigma(n)+1}\frac{\log p}{p-1} - \log n\Biggr) \prod_{p\le \sigma(n)+1} \left(1-\frac{1}{p}\right), }[/math] where [math]\displaystyle{ \gamma }[/math] is the Euler–Mascheroni constant and [math]\displaystyle{ p }[/math] runs over primes.

As with prime numbers in an arithmetic progression, given two natural numbers [math]\displaystyle{ a }[/math] and [math]\displaystyle{ q }[/math], we have [math]\displaystyle{ |\{ n \le x: n \text{ practical and } n\equiv a \bmod q \}|=\frac{c_{q,a} x}{\log x} +O_q\left(\frac{x}{(\log x)^2}\right). }[/math] The constant factor [math]\displaystyle{ c_{q,a} }[/math] is positive if, and only if, there is more than one practical number congruent to [math]\displaystyle{ a \bmod q }[/math]. If [math]\displaystyle{ \gcd(q,a)=\gcd(q,b) }[/math], then [math]\displaystyle{ c_{q,a}=c_{q,b} }[/math]. For example, about 38.26% of practical numbers have a last decimal digit of 0, while the last digits of 2, 4, 6, 8 each occur with the same relative frequency of 15.43%.

References

• Eppstein, David (2021), "Egyptian fractions with denominators from sequences closed under doubling", Journal of Integer Sequences 24: 21.8.8, https://cs.uwaterloo.ca/journals/JIS/VOL24/Eppstein/eppstein2.html 
• "Some problems in partitio numerorum", Journal of the Australian Mathematical Society, Series A 27 (3): 319–331, 1979, doi:10.1017/S144678870001243X .
• Heyworth, M. R. (1980), "More on panarithmic numbers", New Zealand Math. Mag. 17 (1): 24–28 . As cited by (Margenstern 1991).
• Hausman, Miriam; Shapiro, Harold N. (1984), "On practical numbers", Communications on Pure and Applied Mathematics 37 (5): 705–713, doi:10.1002/cpa.3160370507 .
• Margenstern, Maurice (1984), "Résultats et conjectures sur les nombres pratiques", Comptes Rendus de l'Académie des Sciences, Série I 299 (18): 895–898 . As cited by (Margenstern 1991).
• Margenstern, Maurice (1991), "Les nombres pratiques: théorie, observations et conjectures", Journal of Number Theory 37 (1): 1–36, doi:10.1016/S0022-314X(05)80022-8 .
• "A survey on practical numbers", Rend. Sem. Mat. Univ. Pol. Torino 53 (4): 347–359, 1995 .
• Melfi, Giuseppe (1996), "On two conjectures about practical numbers", Journal of Number Theory 56 (1): 205–210, doi:10.1006/jnth.1996.0012 .
• Mitrinović, Dragoslav S.; Sándor, József; Crstici, Borislav (1996), "III.50 Practical numbers", Handbook of number theory, Volume 1, Mathematics and its Applications, 351, Kluwer Academic Publishers, pp. 118–119, ISBN 978-0-7923-3823-9 .
• Pomerance, C.; Weingartner, A. (2021), "On primes and practical numbers", Ramanujan Journal 57 (3): 981–1000, doi:10.1007/s11139-020-00354-y .
• Robinson, D. F. (1979), "Egyptian fractions via Greek number theory", New Zealand Math. Mag. 16 (2): 47–52 . As cited by (Margenstern 1991) and (Mitrinović Sándor).
• Saias, Eric (1997), "Entiers à diviseurs denses, I", Journal of Number Theory 62 (1): 163–191, doi:10.1006/jnth.1997.2057 .
• Sigler, Laurence E. (trans.) (2002), Fibonacci's Liber Abaci, Springer-Verlag, pp. 119–121, ISBN 0-387-95419-8 .
• "Sur une propriété des nombres naturels", Annali di Matematica Pura ed Applicata 39 (1): 69–74, 1955, doi:10.1007/BF02410762 .
• Srinivasan, A. K. (1948), "Practical numbers", Current Science 17: 179–180, http://www.currentscience.ac.in/Downloads/article_id_017_06_0179_0180_0.pdf .
• "Sums of distinct divisors", American Journal of Mathematics (The Johns Hopkins University Press) 76 (4): 779–785, 1954, doi:10.2307/2372651 .
• "Sur un problème de crible et ses applications", Ann. Sci. École Norm. Sup. (4) 19 (1): 1–30, 1986, doi:10.24033/asens.1502 .
• "Length and denominators of Egyptian fractions", Journal of Number Theory 35 (2): 150–156, 1990, doi:10.1016/0022-314X(90)90109-5 .
• Vose, M. (1985), "Egyptian fractions", Bulletin of the London Mathematical Society 17 (1): 21, doi:10.1112/blms/17.1.21 .
• Weingartner, A. (2015), "Practical numbers and the distribution of divisors", The Quarterly Journal of Mathematics 66 (2): 743–758, doi:10.1093/qmath/hav006 .
• Weingartner, A. (2019), "On the constant factor in several related asymptotic estimates", Mathematics of Computation 88 (318): 1883–1902, doi:10.1090/mcom/3402 .
• Weingartner, A. (2020), "The constant factor in the asymptotic for practical numbers", International Journal of Number Theory 16 (3): 629–638, doi:10.1142/S1793042120500311 .
• Weingartner, A. (2021), "An extension of the Siegel-Walfisz theorem", Proceedings of the American Mathematical Society 149 (11): 4699–4708, doi:10.1090/proc/15607 .
• Weingartner, A. (2022), "Somewhat smooth numbers in short intervals", Ramanujan Journal, doi:10.1007/s11139-022-00552-w .

External links

• Tables of practical numbers compiled by Giuseppe Melfi.
• Practical Number at PlanetMath.org.
• Weisstein, Eric W.. "Practical Number". http://mathworld.wolfram.com/PracticalNumber.html.