Hexacontatetragon
| Regular hexacontatetragon | |
|---|---|
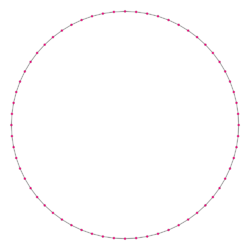 A regular hexacontatetragon | |
| Type | Regular polygon |
| Edges and vertices | 64 |
| Schläfli symbol | {64}, t{32}, tt{16}, ttt{8}, tttt{4} |
| Coxeter diagram |       |
| Symmetry group | Dihedral (D64), order 2×64 |
| Internal angle (degrees) | 174.375° |
| Dual polygon | Self |
| Properties | Convex, cyclic, equilateral, isogonal, isotoxal |
In geometry, a hexacontatetragon (or hexacontakaitetragon) or 64-gon is a sixty-four-sided polygon. (In Greek, the prefix hexaconta- means 60 and tetra- means 4.) The sum of any hexacontatetragon's interior angles is 11160 degrees.
Regular hexacontatetragon
The regular hexacontatetragon can be constructed as a truncated triacontadigon, t{32}, a twice-truncated hexadecagon, tt{16}, a thrice-truncated octagon, ttt{8}, a fourfold-truncated square, tttt{4}, and a fivefold-truncated digon, ttttt{2}.
One interior angle in a regular hexacontatetragon is 1743⁄8°, meaning that one exterior angle would be 55⁄8°.
The area of a regular hexacontatetragon is (with t = edge length)
- [math]\displaystyle{ A = 16t^2 \cot \frac{\pi}{64} }[/math]
and its inradius is
- [math]\displaystyle{ r = \frac{t}{2} \cot \frac{\pi}{64} }[/math]
The circumradius of a regular hexacontatetragon is
- [math]\displaystyle{ R = \frac{t}{2} \csc \frac{\pi}{64} }[/math]
Construction
Since 64 = 26 (a power of two), a regular hexacontatetragon is constructible using a compass and straightedge.[1] As a truncated triacontadigon, it can be constructed by an edge-bisection of a regular triacontadigon.
Symmetry
The regular hexacontatetragon has Dih64 dihedral symmetry, order 128, represented by 64 lines of reflection. Dih64 has 6 dihedral subgroups: Dih32, Dih16, Dih8, Dih4, Dih2 and Dih1 and 7 more cyclic symmetries: Z64, Z32, Z16, Z8, Z4, Z2, and Z1, with Zn representing π/n radian rotational symmetry.
These 13 symmetries generate 20 unique symmetries on the regular hexacontatetragon. John Conway labels these lower symmetries with a letter and order of the symmetry follows the letter.[2] He gives r128 for the full reflective symmetry, Dih64, and a1 for no symmetry. He gives d (diagonal) with mirror lines through vertices, p with mirror lines through edges (perpendicular), i with mirror lines through both vertices and edges, and g for rotational symmetry. a1 labels no symmetry.
These lower symmetries allows degrees of freedoms in defining irregular hexacontatetragons. Only the g64 subgroup has no degrees of freedom but can seen as directed edges.
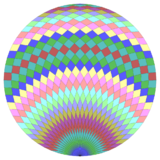
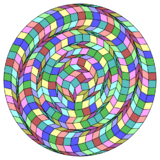
Dissection
Coxeter states that every zonogon (a 2m-gon whose opposite sides are parallel and of equal length) can be dissected into m(m−1)/2 parallelograms.[3] In particular this is true for regular polygons with evenly many sides, in which case the parallelograms are all rhombi. For the regular hexacontatetragon, m=32, and it can be divided into 496: 16 squares and 15 sets of 32 rhombs. This decomposition is based on a Petrie polygon projection of a 32-cube.
|
|
|
Hexacontatetragram
A hexacontatetragram is a 64-sided star polygon. There are 15 regular forms given by Schläfli symbols {64/3}, {64/5}, {64/7}, {64/9}, {64/11}, {64/13}, {64/15}, {64/17}, {64/19}, {64/21}, {64/23}, {64/25}, {64/27}, {64/29}, {64/31}, as well as 16 compound star figures with the same vertex configuration.
| Picture |  {64/3} |
 {64/5} |
 {64/7} |
 {64/9} |
 {64/11} |
 {64/13} |
 {64/15} |
 {64/17} |
|---|---|---|---|---|---|---|---|---|
| Interior angle | 163.125° | 151.875° | 140.625° | 129.375° | 118.125° | 106.875° | 95.625° | 84.375° |
| Picture |  {64/19} |
 {64/21} |
 {64/23} |
 {64/25} |
 {64/27} |
 {64/29} |
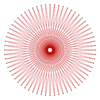 {64/31} |
|
| Interior angle | 73.125° | 61.875° | 50.625° | 39.375° | 28.125° | 16.875° | 5.625° |
References
- ↑ Constructible Polygon
- ↑ John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, (2008) The Symmetries of Things, ISBN:978-1-56881-220-5 (Chapter 20, Generalized Schaefli symbols, Types of symmetry of a polygon pp. 275-278)
- ↑ Coxeter, Mathematical recreations and Essays, Thirteenth edition, p.141
 |
