Triacontatetragon

Short description: Polygon with 34 edges

Regular triacontatetragon
A regular triacontatetragon
Type	Regular polygon
Edges and vertices	34
Schläfli symbol	{34}, t{17}
Coxeter diagram
Symmetry group	Dihedral (D34), order 2×34
Internal angle (degrees)	169.412°
Dual polygon	Self
Properties	Convex, cyclic, equilateral, isogonal, isotoxal

In geometry, a triacontatetragon or triacontakaitetragon is a thirty-four-sided polygon or 34-gon. The sum of any triacontatetragon's interior angles is 5760 degrees.

Regular triacontatetragon

A regular triacontatetragon is represented by Schläfli symbol {34} and can also be constructed as a truncated 17-gon, t{17}, which alternates two types of edges.

One interior angle in a regular triacontatetragon is (2880/17)°, meaning that one exterior angle would be (180/17)°.

The area of a regular triacontatetragon is (with t = edge length)

[math]\displaystyle{ A = \frac{17}{2}t^2 \cot \frac{\pi}{34} }[/math]

and its inradius is

[math]\displaystyle{ r = \frac{1}{2}t \cot \frac{\pi}{34} }[/math]

The factor [math]\displaystyle{ \cot \frac{\pi}{34} }[/math] is a root of the equation [math]\displaystyle{ x^{16} - 136x^{14} + 2 380x^{12} - 12 376x^{10} + 24 310x^{8} - 19 448x^{6} + 6 188x^{4} - 680x^{2} + 17=0 }[/math].

The circumradius of a regular triacontatetragon is

[math]\displaystyle{ R = \frac{1}{2}t \csc \frac{\pi}{34} }[/math]

As 34 = 2 × 17 and 17 is a Fermat prime, a regular triacontatetragon is constructible using a compass and straightedge. As a truncated 17-gon, it can be constructed by an edge-bisection of a regular 17-gon. This means that the values of [math]\displaystyle{ \sin \frac{\pi}{34} }[/math] and [math]\displaystyle{ \cos \frac{\pi}{34} }[/math] may be expressed in terms of nested radicals.

Symmetry

The regular triacontatetragon has Dih₃₄ symmetry, order 68. There are 3 subgroup dihedral symmetries: Dih₁₇, Dih₂, and Dih₁, and 4 cyclic group symmetries: Z₃₄, Z₁₇, Z₂, and Z₁.

These 8 symmetries can be seen in 10 distinct symmetries on the icosidigon, a larger number because the lines of reflections can either pass through vertices or edges. John Conway labels these by a letter and group order. The full symmetry of the regular form is labeled r68 and no symmetry is labeled a1. The dihedral symmetries are divided depending on whether they pass through vertices (d for diagonal) or edges (p for perpendiculars), and i when reflection lines path through both edges and vertices. Cyclic symmetries n are labeled as g for their central gyration orders.

Each subgroup symmetry allows one or more degrees of freedom for irregular forms. Only the g34 subgroup has no degrees of freedom but can seen as directed edges.

The highest symmetry irregular triacontatetragons are d34, an isogonal triacontatetragon constructed by seventeen mirrors which can alternate long and short edges, and p34, an isotoxal triacontatetragon, constructed with equal edge lengths, but vertices alternating two different internal angles. These two forms are duals of each other and have half the symmetry order of the regular triacontatetragon.

Dissection

34-gon with 544 rhombs

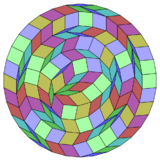
Coxeter states that every zonogon (a 2m-gon whose opposite sides are parallel and of equal length) can be dissected into m(m-1)/2 parallelograms. In particular this is true for regular polygons with evenly many sides, in which case the parallelograms are all rhombi. For the regular triacontatetragon, m=17, it can be divided into 136: 8 sets of 17 rhombs. This decomposition is based on a Petrie polygon projection of a 17-cube.

Examples

Triacontatetragram

A triacontatetragram is a 34-sided star polygon. There are seven regular forms given by Schläfli symbols {34/3}, {34/5}, {34/7}, {34/9}, {34/11}, {34/13}, and {34/15}, and nine compound star figures with the same vertex configuration.

{34/3}

{34/5}

{34/7}

{34/9}

{34/11}

{34/13}

{34/15}

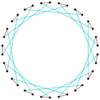
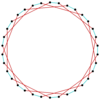
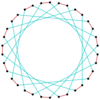
Many isogonal triacontatetragrams can also be constructed as deeper truncations of the regular heptadecagon {17} and heptadecagrams {17/2}, {17/3}, {17/4}, {17/5}, {17/6}, {17/7}, and {17/8}. These also create eight quasitruncations: t{17/9} = {34/9}, t{17/10} = {34/10}, t{17/11} = {34/11}, t{17/12} = {34/12}, t{17/13} = {34/13}, t{17/14} = {34/14}, t{17/15} = {34/15}, and t{17/16} = {34/16}. Some of the isogonal triacontatetragrams are depicted below, as a truncation sequence with endpoints t{17}={34} and t{17/16}={34/16}.

t{17}={34}									t{17/16}={34/16}
t{17/3}={34/3}									t{17/14}={34/14}
t{17/5}={34/5}								t{17/12}={34/12}	t{17/12}={34/12}
t{17/7}={34/7}									t{17/10}={34/5}
t{17/9}={34/9}									t{17/8}={34/8}