Tetracontagon

From HandWiki
Short description: Polygon with 40 edges
Regular tetracontagon
Regular polygon 40.svg
A regular tetracontagon
TypeRegular polygon
Edges and vertices40
Schläfli symbol{40}, t{20}, tt{10}, ttt{5}
Coxeter diagramCDel node 1.pngCDel 4.pngCDel 0x.pngCDel node.png
CDel node 1.pngCDel 20.pngCDel node 1.png
Symmetry groupDihedral (D40), order 2×40
Internal angle (degrees)171°
Dual polygonSelf
PropertiesConvex, cyclic, equilateral, isogonal, isotoxal

In geometry, a tetracontagon or tessaracontagon is a forty-sided polygon or 40-gon.[1][2] The sum of any tetracontagon's interior angles is 6840 degrees.

Regular tetracontagon

A regular tetracontagon is represented by Schlafli symbol {40} and can also be constructed as a truncated icosagon, t{20}, which alternates 2 types of edges. Furthermore, it can also be constructed as a twice-truncated decagon, tt{10}, or a thrice-truncated pentagon, ttt{5}.

One interior angle in a regular tetracontagon is 171°, meaning that one exterior angle would be 9°.

The area of a regular tetracontagon is (with t = edge length)

[math]\displaystyle{ \begin{align}A = 10t^2 \cot \frac{\pi}{40}=&10\left(1+\sqrt{5}+\sqrt{5+2\sqrt{5}}+\sqrt{\left(1+\sqrt{5}+\sqrt{5+2\sqrt{5}}\right)^2+1}\right)t^2\\ =&10\left(1+\sqrt{5}+\sqrt{5+2\sqrt{5}}+\sqrt{\left(1+\sqrt{5}\right)^2+\binom{2}{1}\left(1+\sqrt{5}\right)\sqrt{5+2\sqrt{5}}+\left(\sqrt{5+2\sqrt{5}}\right)^2+1}\right)t^2\\ =&10\left(1+\sqrt{5}+\sqrt{5+2\sqrt{5}}+\sqrt{\left(6+\binom{2}{1}\sqrt{5}\right)^{}+\binom{2}{1}\left(1+\sqrt{5}\right)\sqrt{5+2\sqrt{5}}+\left(5+2\sqrt{5}\right)^{}+1}\right)t^2\\ =&10\left(1+\sqrt{5}+\sqrt{5+2\sqrt{5}}+\sqrt{\left(11+4\sqrt{5}+\binom{2}{1}\left(1+\sqrt{5}\right)\sqrt{5+2\sqrt{5}}\right)+1}\right)t^2\\ =&10\left(1+\sqrt{5}+\sqrt{5+2\sqrt{5}}+\sqrt{12+4\sqrt{5}+\binom{2}{1}\left(1+\sqrt{5}\right)\sqrt{5+2\sqrt{5}}}\right)t^2\end{align} }[/math]

and its inradius is

[math]\displaystyle{ r = \frac{1}{2}t \cot \frac{\pi}{40} }[/math]

The factor [math]\displaystyle{ \cot \frac{\pi}{40} }[/math] is a root of the octic equation [math]\displaystyle{ x^{8} - 8x^{7} - 60x^{6} - 8x^{5} + 134x^{4} + 8x^{3} - 60x^{2} + 8x + 1 }[/math].

The circumradius of a regular tetracontagon is

[math]\displaystyle{ \begin{align}R = \frac{1}{2}t \csc \frac{\pi}{40}\end{align} }[/math]

As 40 = 23 × 5, a regular tetracontagon is constructible using a compass and straightedge.[3] As a truncated icosagon, it can be constructed by an edge-bisection of a regular icosagon. This means that the values of [math]\displaystyle{ \sin \frac{\pi}{40} }[/math] and [math]\displaystyle{ \cos \frac{\pi}{40} }[/math] may be expressed in radicals as follows:

[math]\displaystyle{ \sin \frac{\pi}{40} = \frac{1}{4}(\sqrt{2}-1)\sqrt{\frac{1}{2}(2+\sqrt{2})(5+\sqrt{5})}-\frac{1}{8}\sqrt{2-\sqrt{2}}(1+\sqrt{2})(\sqrt{5}-1) }[/math]
[math]\displaystyle{ \cos \frac{\pi}{40} = \frac{1}{8}(\sqrt{2}-1)\sqrt{2+\sqrt{2}}(\sqrt{5}-1)+\frac{1}{4}(1+\sqrt{2})\sqrt{\frac{1}{2}(2-\sqrt{2})(5+\sqrt{5})} }[/math]

Construction of a regular tetracontagon

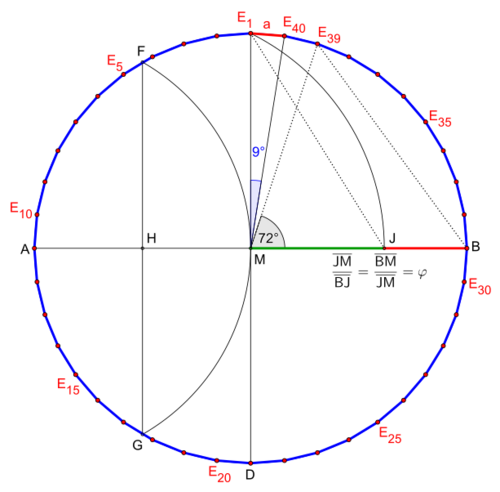
Regular tetracontagon with given circumcircle

Circumcircle is given

  1. Construct first the side length JE1 of a pentagon.
  2. Transfer this on the circumcircle, there arises the intersection E39.
  3. Connect the point E39 with the central point M, there arises the angle E39ME1 with 72°.
  4. Halve the angle E39ME1, there arise the intersection E40 and the angle E40ME1 with 9°.
  5. Connect the point E1 with the point E40, there arises the first side length a of the tetracontagon.
  6. Finally you transfer the segment E1E40 (side length a) repeatedly counterclockwise on the circumcircle until arises a regular tetracontagon.

The golden ratio

[math]\displaystyle{ \frac{\overline{JM}}{\overline{BJ}} = \frac{\overline{BM}}{\overline{JM}} = \frac{1 + \sqrt{5}}{2}= \varphi \approx 1.618 }[/math]

Side length is given

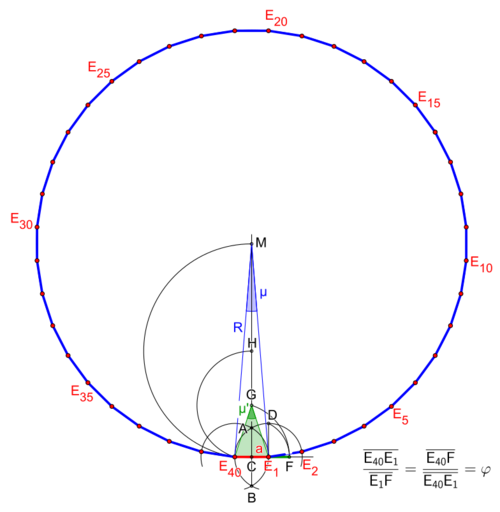
Regular tetracontagon with given side length
(The construction is very similar to that of icosagon with given side length)
  1. Draw a segment E40E1 whose length is the given side length a of the tetracontagon.
  2. Extend the segment E40E1 by more than two times.
  3. Draw each a circular arc about the points E1 and E40, there arise the intersections A and B.
  4. Draw a vertical straight line from point B through point A.
  5. Draw a parallel line too the segment AB from the point E1 to the circular arc, there arises the intersection D.
  6. Draw a circle arc about the point C with the radius CD till to the extension of the side length, there arises the intersection F.
  7. Draw a circle arc about the point E40 with the radius E40F till to the vertical straight line, there arises the intersection G and the angle E40GE1 with 36°.
  8. Draw a circle arc about the point G with radius E40G till to the vertical straight line, there arises the intersection H and the angle E40HE1 with 18°.
  9. Draw a circle arc about the point H with radius E40H till to the vertical straight line, there arises the central point M of the circumcircle and the angle E40ME1 with 9°.
  10. Draw around the central point M with radius E40M the circumcircle of the tetracontagon.
  11. Finally transfer the segment E40E1 (side length a) repeatedly counterclockwise on the circumcircle until to arises a regular tetracontagon.

The golden ratio

[math]\displaystyle{ \frac{\overline{E_{40}E_1}}{\overline{E_1F}} = \frac{\overline{E_{40}F}}{\overline{E_{40}E_1}} = \frac{1 + \sqrt{5}}{2}= \varphi \approx 1.618 }[/math]

Symmetry

The symmetries of a regular tetracontagon. Light blue lines show subgroups of index 2. The left and right subgraphs are positionally related by index 5 subgroups.

The regular tetracontagon has Dih40 dihedral symmetry, order 80, represented by 40 lines of reflection. Dih40 has 7 dihedral subgroups: (Dih20, Dih10, Dih5), and (Dih8, Dih4, Dih2, Dih1). It also has eight more cyclic symmetries as subgroups: (Z40, Z20, Z10, Z5), and (Z8, Z4, Z2, Z1), with Zn representing π/n radian rotational symmetry.

John Conway labels these lower symmetries with a letter and order of the symmetry follows the letter.[4] He gives d (diagonal) with mirror lines through vertices, p with mirror lines through edges (perpendicular), i with mirror lines through both vertices and edges, and g for rotational symmetry. a1 labels no symmetry.

These lower symmetries allows degrees of freedoms in defining irregular tetracontagons. Only the g40 subgroup has no degrees of freedom but can seen as directed edges.

Dissection

40-gon with 560 rhombs
40-gon rhombic dissection-size2.svg
regular 		Isotoxal 40-gon rhombic dissection-size2.svg
Isotoxal

Coxeter states that every zonogon (a 2m-gon whose opposite sides are parallel and of equal length) can be dissected into m(m-1)/2 parallelograms. These tilings are contained as subsets of vertices, edges and faces in orthogonal projections m-cubes[5] In particular this is true for regular polygons with evenly many sides, in which case the parallelograms are all rhombi. For the regular tetracontagon, m=20, and it can be divided into 190: 10 squares and 9 sets of 20 rhombs. This decomposition is based on a Petrie polygon projection of a 20-cube.

Examples
40-gon rhombic dissection.svg 40-gon rhombic dissection2.svg 40-gon rhombic dissectionx.svg

Tetracontagram

A tetracontagram is a 40-sided star polygon. There are seven regular forms given by Schläfli symbols {40/3}, {40/7}, {40/9}, {40/11}, {40/13}, {40/17}, and {40/19}, and 12 compound star figures with the same vertex configuration.

Regular star polygons {40/k}
Picture Star polygon 40-3.svg
{40/3} 		Star polygon 40-7.svg
{40/7} 		Star polygon 40-9.svg
{40/9} 		Star polygon 40-11.svg
{40/11} 		Star polygon 40-13.svg
{40/13} 		Star polygon 40-17.svg
{40/17} 		Star polygon 40-19.svg
{40/19}
Interior angle 153° 117° 99° 81° 63° 27° 9°
Regular compound polygons
Picture Star polygon 40-2.png
{40/2}=2{20} 		Star polygon 40-4.png
{40/4}=4{10} 		Star polygon 40-5.png
{40/5}=5{8} 		Star polygon 40-6.png
{40/6}=2{20/3} 		Star polygon 40-8.png
{40/8}=8{5} 		Star polygon 40-10.png
{40/10}=10{4}
Interior angle 162° 144° 135° 126° 108° 90°
Picture Star polygon 40-12.png
{40/12}=4{10/3} 		Star polygon 40-14.png
{40/14}=2{20/7} 		Star polygon 40-15.png
{40/15}=5{8/3} 		Star polygon 40-16.png
{40/16}=8{5/2} 		Star polygon 40-18.png
{40/18}=2{20/9} 		Star polygon 40-20.png
{40/20}=20{2}
Interior angle 72° 54° 45° 36° 18° 0°

Many isogonal tetracontagrams can also be constructed as deeper truncations of the regular icosagon {20} and icosagrams {20/3}, {20/7}, and {20/9}. These also create four quasitruncations: t{20/11}={40/11}, t{20/13}={40/13}, t{20/17}={40/17}, and t{20/19}={40/19}. Some of the isogonal tetracontagrams are depicted below, as a truncation sequence with endpoints t{20}={40} and t{20/19}={40/19}.[6]

Regular polygon truncation 20 1.svg
t{20}={40}
CDel node 1.pngCDel 20.pngCDel node 1.png 		Regular polygon truncation 20 2.svg Regular polygon truncation 20 3.svg Regular polygon truncation 20 4.svg Regular polygon truncation 20 5.svg Regular polygon truncation 20 6.svg
Regular polygon truncation 20 7.svg Regular polygon truncation 20 8.svg Regular polygon truncation 20 9.svg Regular polygon truncation 20 10.svg Regular polygon truncation 20 11.svg
t{20/19}={40/19}
CDel node 1.pngCDel 20.pngCDel rat.pngCDel 19.pngCDel node 1.png

References

  1. ↑ Gorini, Catherine A. (2009), The Facts on File Geometry Handbook, Infobase Publishing, p. 165, ISBN 9781438109572, https://books.google.com/books?id=PlYCcvgLJxYC&pg=PA165 .
  2. ↑ The New Elements of Mathematics: Algebra and Geometry by Charles Sanders Peirce (1976), p.298
  3. ↑ Constructible Polygon
  4. ↑ The Symmetries of Things, Chapter 20
  5. ↑ Coxeter, Mathematical recreations and Essays, Thirteenth edition, p.141
  6. ↑ The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History, (1994), Metamorphoses of polygons, Branko Grünbaum

External links




Retrieved from "https://handwiki.org/wiki/index.php?title=Tetracontagon&oldid=60155"