Physics:Instanton
An instanton (or pseudoparticle[1][2][3]) is a notion appearing in theoretical and mathematical physics. An instanton is a classical solution to equations of motion with a finite, non-zero action, either in quantum mechanics or in quantum field theory. More precisely, it is a solution to the equations of motion of the classical field theory on a Euclidean spacetime.[4]
In such quantum theories, solutions to the equations of motion may be thought of as critical points of the action. The critical points of the action may be local maxima of the action, local minima, or saddle points. Instantons are important in quantum field theory because:
- they appear in the path integral as the leading quantum corrections to the classical behavior of a system, and
- they can be used to study the tunneling behavior in various systems such as a Yang–Mills theory.
Relevant to dynamics, families of instantons permit that instantons, i.e. different critical points of the equation of motion, be related to one another. In physics instantons are particularly important because the condensation of instantons (and noise-induced anti-instantons) is believed to be the explanation of the noise-induced chaotic phase known as self-organized criticality.
Mathematics
Mathematically, a Yang–Mills instanton is a self-dual or anti-self-dual connection in a principal bundle over a four-dimensional Riemannian manifold that plays the role of physical space-time in non-abelian gauge theory. Instantons are topologically nontrivial solutions of Yang–Mills equations that absolutely minimize the energy functional within their topological type.[5] The first such solutions were discovered in the case of four-dimensional Euclidean space compactified to the four-dimensional sphere, and turned out to be localized in space-time, prompting the names pseudoparticle and instanton.
Yang–Mills instantons have been explicitly constructed in many cases by means of twistor theory, which relates them to algebraic vector bundles on algebraic surfaces, and via the ADHM construction, or hyperkähler reduction (see hyperkähler manifold), a geometric invariant theory procedure. The groundbreaking work of Simon Donaldson, for which he was later awarded the Fields medal, used the moduli space of instantons over a given four-dimensional differentiable manifold as a new invariant of the manifold that depends on its differentiable structure and applied it to the construction of homeomorphic but not diffeomorphic four-manifolds. Many methods developed in studying instantons have also been applied to monopoles. This is because magnetic monopoles arise as solutions of a dimensional reduction of the Yang–Mills equations.[6]
Quantum mechanics
An instanton can be used to calculate the transition probability for a quantum mechanical particle tunneling through a potential barrier. One example of a system with an instanton effect is a particle in a double-well potential. In contrast to a classical particle, there is non-vanishing probability that it crosses a region of potential energy higher than its own energy.[4]
Motivation of considering instantons
Consider the quantum mechanics of a single particle motion inside the double-well potential [math]\displaystyle{ V(x)={1\over 4}(x^2-1)^2. }[/math] The potential energy takes its minimal value at [math]\displaystyle{ x=\pm 1 }[/math], and these are called classical minima because the particle tends to lie in one of them in classical mechanics. There are two lowest energy states in classical mechanics.
In quantum mechanics, we solve the Schrödinger equation
- [math]\displaystyle{ -{\hbar^2\over 2m}{\partial^2\over \partial x^2}\psi(x)+V(x)\psi(x)=E\psi(x), }[/math]
to identify the energy eigenstates. If we do this, we will find only the unique lowest-energy state instead of two states. The ground-state wave function localizes at both of the classical minima [math]\displaystyle{ x=\pm 1 }[/math] instead of only one of them because of the quantum interference or quantum tunneling.
Instantons are the tool to understand why this happens within the semi-classical approximation of the path-integral formulation in Euclidean time. We will first see this by using the WKB approximation that approximately computes the wave function itself, and will move on to introduce instantons by using the path integral formulation.
WKB approximation
One way to calculate this probability is by means of the semi-classical WKB approximation, which requires the value of [math]\displaystyle{ \hbar }[/math] to be small. The time independent Schrödinger equation for the particle reads
- [math]\displaystyle{ \frac{d^2\psi}{dx^2}=\frac{2m(V(x)-E)}{\hbar^2}\psi. }[/math]
If the potential were constant, the solution would be a plane wave, up to a proportionality factor,
- [math]\displaystyle{ \psi = \exp(-\mathrm{i}kx)\, }[/math]
with
- [math]\displaystyle{ k=\frac{\sqrt{2m(E-V)}}{\hbar}. }[/math]
This means that if the energy of the particle is smaller than the potential energy, one obtains an exponentially decreasing function. The associated tunneling amplitude is proportional to
- [math]\displaystyle{ e^{-\frac{1}{\hbar}\int_a^b\sqrt{2m(V(x)-E)} \, dx}, }[/math]
where a and b are the beginning and endpoint of the tunneling trajectory.
Path integral interpretation via instantons
Alternatively, the use of path integrals allows an instanton interpretation and the same result can be obtained with this approach. In path integral formulation, the transition amplitude can be expressed as
- [math]\displaystyle{ K(a,b;t)=\langle x=a|e^{-\frac{i\mathbb{H}t}{\hbar}}|x=b\rangle =\int d[x(t)]e^{\frac{iS[x(t)]}{\hbar}}. }[/math]
Following the process of Wick rotation (analytic continuation) to Euclidean spacetime ([math]\displaystyle{ it\rightarrow \tau }[/math]), one gets
- [math]\displaystyle{ K_E(a,b;\tau)=\langle x=a|e^{-\frac{\mathbb{H}\tau}{\hbar}}|x=b\rangle =\int d[x(\tau)]e^{-\frac{S_E[x(\tau)]}{\hbar}}, }[/math]
with the Euclidean action
- [math]\displaystyle{ S_E=\int_{\tau_a}^{\tau_b}\left(\frac{1}{2}m\left(\frac{dx}{d\tau}\right)^2+V(x)\right) d\tau. }[/math]
The potential energy changes sign [math]\displaystyle{ V(x) \rightarrow - V(x) }[/math] under the Wick rotation and the minima transform into maxima, thereby [math]\displaystyle{ V(x) }[/math] exhibits two "hills" of maximal energy.
Let us now consider the local minimum of the Euclidean action [math]\displaystyle{ S_E }[/math] with the double-well potential [math]\displaystyle{ V(x)={1\over 4}(x^2-1)^2 }[/math], and we set [math]\displaystyle{ m=1 }[/math] just for simplicity of computation. Since we want to know how the two classically lowest energy states [math]\displaystyle{ x=\pm1 }[/math] are connected, let us set [math]\displaystyle{ a=-1 }[/math] and [math]\displaystyle{ b=1 }[/math]. For [math]\displaystyle{ a=-1 }[/math] and [math]\displaystyle{ b=1 }[/math], we can rewrite the Euclidean action as
- [math]\displaystyle{ S_E=\int_{\tau_a}^{\tau_b}d \tau {1\over 2}\left({d x\over d \tau}-\sqrt{2V(x)}\right)^2 + \sqrt{2}\int_{\tau_a}^{\tau_b}d \tau{d x\over d \tau}\sqrt{V(x)} }[/math]
- [math]\displaystyle{ \quad =\int_{\tau_a}^{\tau_b}d \tau {1\over 2}\left({d x\over d \tau}-\sqrt{2V(x)}\right)^2 + \int_{-1}^{1}d x {1\over \sqrt{2}}(1-x^2). }[/math]
- [math]\displaystyle{ \quad \ge {2\sqrt{2}\over 3}. }[/math]
The above inequality is saturated by the solution of [math]\displaystyle{ {d x\over d \tau}=\sqrt{2V(x)} }[/math] with the condition [math]\displaystyle{ x(\tau_a)=-1 }[/math] and [math]\displaystyle{ x(\tau_b)=1 }[/math]. Such solutions exist, and the solution takes the simple form when [math]\displaystyle{ \tau_a=-\infty }[/math] and [math]\displaystyle{ \tau_b=\infty }[/math]. The explicit formula for the instanton solution is given by
- [math]\displaystyle{ x(\tau)=\tanh\left({1\over \sqrt{2}}(\tau-\tau_0)\right). }[/math]
Here [math]\displaystyle{ \tau_0 }[/math] is an arbitrary constant. Since this solution jumps from one classical vacuum [math]\displaystyle{ x=-1 }[/math] to another classical vacuum [math]\displaystyle{ x=1 }[/math] instantaneously around [math]\displaystyle{ \tau=\tau_0 }[/math], it is called an instanton.
Explicit formula for double-well potential
The explicit formula for the eigenenergies of the Schrödinger equation with double-well potential has been given by Müller–Kirsten[7] with derivation by both a perturbation method (plus boundary conditions) applied to the Schrödinger equation, and explicit derivation from the path integral (and WKB). The result is the following. Defining parameters of the Schrödinger equation and the potential by the equations
- [math]\displaystyle{ \frac{d^2y(z)}{dz^2} + [E-V(z)]y(z) = 0, }[/math]
and
- [math]\displaystyle{ V(z) = -\frac{1}{4}z^2h^4 + \frac{1}{2}c^2z^4, \;\;\; c^2\gt 0, \; h^4\gt 0, }[/math]
the eigenvalues for [math]\displaystyle{ q_0=1,3,5,... }[/math] are found to be:
- [math]\displaystyle{ E_{\pm}(q_0,h^2) = -\frac{h^8}{2^5c^2} + \frac{1}{\sqrt{2}}q_0h^2 - \frac{c^2(3q^2_0+1)}{2h^4} - \frac{\sqrt{2}c^4q_0}{8h^{10}}(17q^2_0+19) +O(\frac{1}{h^{16}}) }[/math]
- [math]\displaystyle{ \mp \frac{2^{q_0+1}h^2(h^6/2c^2)^{q_0/2}}{\sqrt{\pi}2^{q_0/4}[(q_0-1)/2]!} e^{-h^6/6\sqrt{2}c^2}. }[/math]
Clearly these eigenvalues are asymptotically ([math]\displaystyle{ h^2\rightarrow\infty }[/math]) degenerate as expected as a consequence of the harmonic part of the potential.
Results
Results obtained from the mathematically well-defined Euclidean path integral may be Wick-rotated back and give the same physical results as would be obtained by appropriate treatment of the (potentially divergent) Minkowskian path integral. As can be seen from this example, calculating the transition probability for the particle to tunnel through a classically forbidden region ([math]\displaystyle{ V(x) }[/math]) with the Minkowskian path integral corresponds to calculating the transition probability to tunnel through a classically allowed region (with potential −V(X)) in the Euclidean path integral (pictorially speaking – in the Euclidean picture – this transition corresponds to a particle rolling from one hill of a double-well potential standing on its head to the other hill). This classical solution of the Euclidean equations of motion is often named "kink solution" and is an example of an instanton. In this example, the two "vacua" (i.e. ground states) of the double-well potential, turn into hills in the Euclideanized version of the problem.
Thus, the instanton field solution of the (Euclidean, i. e., with imaginary time) (1 + 1)-dimensional field theory – first quantized quantum mechanical description – allows to be interpreted as a tunneling effect between the two vacua (ground states – higher states require periodic instantons) of the physical (1-dimensional space + real time) Minkowskian system. In the case of the double-well potential written
- [math]\displaystyle{ V(\phi) = \frac{m^4}{2g^2}\left(1 - \frac{g^2\phi^2}{m^2}\right)^2 }[/math]
the instanton, i.e. solution of
- [math]\displaystyle{ \frac{d^2\phi}{d\tau^2} = V'(\phi), }[/math]
(i.e. with energy [math]\displaystyle{ E_{cl} = 0 }[/math]), is
- [math]\displaystyle{ \phi_c(\tau) = \frac{m}{g}\tanh\left[m(\tau - \tau_0)\right], }[/math]
where [math]\displaystyle{ \tau = it }[/math] is the Euclidean time.
Note that a naïve perturbation theory around one of those two vacua alone (of the Minkowskian description) would never show this non-perturbative tunneling effect, dramatically changing the picture of the vacuum structure of this quantum mechanical system. In fact the naive perturbation theory has to be supplemented by boundary conditions, and these supply the nonperturbative effect, as is evident from the above explicit formula and analogous calculations for other potentials such as a cosine potential (cf. Mathieu function) or other periodic potentials (cf. e.g. Lamé function and spheroidal wave function) and irrespective of whether one uses the Schrödinger equation or the path integral.[8]
Therefore, the perturbative approach may not completely describe the vacuum structure of a physical system. This may have important consequences, for example, in the theory of "axions" where the non-trivial QCD vacuum effects (like the instantons) spoil the Peccei–Quinn symmetry explicitly and transform massless Nambu–Goldstone bosons into massive pseudo-Nambu–Goldstone ones.
Periodic instantons
In one-dimensional field theory or quantum mechanics one defines as "instanton" a field configuration which is a solution of the classical (Newton-like) equation of motion with Euclidean time and finite Euclidean action. In the context of soliton theory the corresponding solution is known as a kink. In view of their analogy with the behaviour of classical particles such configurations or solutions, as well as others, are collectively known as pseudoparticles or pseudoclassical configurations. The "instanton" (kink) solution is accompanied by another solution known as "anti-instanton" (anti-kink), and instanton and anti-instanton are distinguished by "topological charges" +1 and −1 respectively, but have the same Euclidean action.
"Periodic instantons" are a generalization of instantons.[9] In explicit form they are expressible in terms of Jacobian elliptic functions which are periodic functions (effectively generalisations of trigonometrical functions). In the limit of infinite period these periodic instantons – frequently known as "bounces", "bubbles" or the like – reduce to instantons.
The stability of these pseudoclassical configurations can be investigated by expanding the Lagrangian defining the theory around the pseudoparticle configuration and then investigating the equation of small fluctuations around it. For all versions of quartic potentials (double-well, inverted double-well) and periodic (Mathieu) potentials these equations were discovered to be Lamé equations, see Lamé function.[10] The eigenvalues of these equations are known and permit in the case of instability the calculation of decay rates by evaluation of the path integral.[9]
Instantons in reaction rate theory
In the context of reaction rate theory periodic instantons are used to calculate the rate of tunneling of atoms in chemical reactions. The progress of a chemical reaction can be described as the movement of a pseudoparticle on a high dimensional potential energy surface (PES). The thermal rate constant [math]\displaystyle{ k }[/math] can then be related to the imaginary part of the free energy [math]\displaystyle{ F }[/math] by
[math]\displaystyle{ k(\beta) = -\frac{2}{\hbar} \text{Im} \mathrm{F} = \frac{2}{\beta \hbar} \text{Im} \ \text{ln}(Z_k) \approx \frac{2}{\hbar \beta} \frac{\text{Im} Z_k }{\text{Re} Z_k } ,\ \ \text{Re} Z_k \gg \text{Im} Z_k }[/math]
whereby [math]\displaystyle{ Z_k }[/math]is the canonical partition function which is calculated by taking the trace of the Boltzmann operator in the position representation.
[math]\displaystyle{ Z_k = \text{Tr}(e^{-\beta \hat{H}}) = \int d\mathbf{x} \left\langle \mathbf{x} \left| e^{-\beta \hat{H}} \right| \mathbf{x} \right\rangle }[/math]
Using a wick rotation and identifying the Euclidean time with [math]\displaystyle{ \hbar\beta = 1/(k_b T) }[/math] one obtains a path integral representation for the partition function in mass weighted coordinates
- [math]\displaystyle{ Z_k = \oint \mathcal{D} \mathbf{x}(\tau) e^{-S_E[\mathbf{x}(\tau)]/\hbar}, \ \ \ S_E = \int_0^{\beta \hbar} \left( \frac{\dot{\mathbf{x}}}{2}^2 + V(\mathbf{x}(\tau)) \right) d\tau }[/math]
The path integral is then approximated via a steepest descent integration which takes only into account the contributions from the classical solutions and quadratic fluctuations around them. This yields for the rate constant expression in mass weighted coordinates
[math]\displaystyle{ k(\beta) = \frac{2}{\beta\hbar} \left( \frac{ \text{det}\left[ -\frac{\partial^2}{\partial \tau^2} + \mathbf{V}''(x_\text{RS}(\tau)) \right] }{\text{det} \left[- \frac{\partial^2}{\partial \tau^2} + \mathbf{V}''(x_\text{Inst}(\tau)) \right] } \right)^\frac{1}{2}{\exp\left({\frac{-S_E[x_\text{inst}(\tau) + S_E[x_\text{RS}(\tau)] }{\hbar}}\right)} }[/math]
where [math]\displaystyle{ \mathbf{x}_\text{Inst} }[/math]is a periodic instanton and [math]\displaystyle{ \mathbf{x}_\text{RS} }[/math]is the trivial solution of the pseudoparticle at rest which represents the reactant state configuration.
Inverted double-well formula
As for the double-well potential one can derive the eigenvalues for the inverted double-well potential. In this case, however, the eigenvalues are complex. Defining parameters by the equations
- [math]\displaystyle{ \frac{d^2y}{dz^2} + [E - V(z)]y(z) = 0, \;\;\; V(z) = \frac{1}{4}h^4z^2 - \frac{1}{2}c^2z^4, }[/math]
the eigenvalues as given by Müller-Kirsten are, for [math]\displaystyle{ q_0 = 1,3,5,..., }[/math]
- [math]\displaystyle{ E = \frac{1}{2}q_0h^2 - \frac{3c^2}{4h^4}(q^2_0+1) -\frac{q_0c^4}{h^{10}}(4q^2_0+29) + O(\frac{1}{h^{16}}) \pm i\frac{2^{q_0}h^2(h^6/2c^2)^{q_0/2}}{(2\pi)^{1/2}[(q_0-1)/2]!}e^{-h^6/6c^2}. }[/math]
The imaginary part of this expression agrees with the well known result of Bender and Wu.[11] In their notation [math]\displaystyle{ \hbar = 1, q_0=2K+1, h^6/2c^2 = \epsilon. }[/math]
Quantum field theory
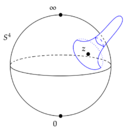
| Hypersphere [math]\displaystyle{ S^3 }[/math] | |
|---|---|
 Hypersphere Stereographic projection Parallels (red), meridians (blue) and hypermeridians (green).[note 1] | |
In studying quantum field theory (QFT), the vacuum structure of a theory may draw attention to instantons. Just as a double-well quantum mechanical system illustrates, a naïve vacuum may not be the true vacuum of a field theory. Moreover, the true vacuum of a field theory may be an "overlap" of several topologically inequivalent sectors, so called "topological vacua".
A well understood and illustrative example of an instanton and its interpretation can be found in the context of a QFT with a non-abelian gauge group,[note 2] a Yang–Mills theory. For a Yang–Mills theory these inequivalent sectors can be (in an appropriate gauge) classified by the third homotopy group of SU(2) (whose group manifold is the 3-sphere [math]\displaystyle{ S^3 }[/math]). A certain topological vacuum (a "sector" of the true vacuum) is labelled by an unaltered transform, the Pontryagin index. As the third homotopy group of [math]\displaystyle{ S^3 }[/math] has been found to be the set of integers,
- [math]\displaystyle{ \pi 3 }[/math][math]\displaystyle{ (S^3)= }[/math][math]\displaystyle{ \mathbb{Z}\, }[/math]
there are infinitely many topologically inequivalent vacua, denoted by [math]\displaystyle{ |N\rangle }[/math], where [math]\displaystyle{ N }[/math] is their corresponding Pontryagin index. An instanton is a field configuration fulfilling the classical equations of motion in Euclidean spacetime, which is interpreted as a tunneling effect between these different topological vacua. It is again labelled by an integer number, its Pontryagin index, [math]\displaystyle{ Q }[/math]. One can imagine an instanton with index [math]\displaystyle{ Q }[/math] to quantify tunneling between topological vacua [math]\displaystyle{ |N\rangle }[/math] and [math]\displaystyle{ |N+Q\rangle }[/math]. If Q = 1, the configuration is named BPST instanton after its discoverers Alexander Belavin, Alexander Polyakov, Albert S. Schwarz and Yu. S. Tyupkin. The true vacuum of the theory is labelled by an "angle" theta and is an overlap of the topological sectors:
- [math]\displaystyle{ |\theta\rangle =\sum_{N=-\infty}^{N=+\infty}e^{i \theta N}|N\rangle. }[/math]
Gerard 't Hooft first performed the field theoretic computation of the effects of the BPST instanton in a theory coupled to fermions in [1]. He showed that zero modes of the Dirac equation in the instanton background lead to a non-perturbative multi-fermion interaction in the low energy effective action.
Yang–Mills theory
The classical Yang–Mills action on a principal bundle with structure group G, base M, connection A, and curvature (Yang–Mills field tensor) F is
- [math]\displaystyle{ S_{YM} = \int_M \left|F\right|^2 d\mathrm{vol}_M, }[/math]
where [math]\displaystyle{ d\mathrm{vol}_M }[/math] is the volume form on [math]\displaystyle{ M }[/math]. If the inner product on [math]\displaystyle{ \mathfrak{g} }[/math], the Lie algebra of [math]\displaystyle{ G }[/math] in which [math]\displaystyle{ F }[/math] takes values, is given by the Killing form on [math]\displaystyle{ \mathfrak{g} }[/math], then this may be denoted as [math]\displaystyle{ \int_M \mathrm{Tr}(F \wedge *F) }[/math], since
- [math]\displaystyle{ F \wedge *F = \langle F, F \rangle d\mathrm{vol}_M. }[/math]
For example, in the case of the gauge group U(1), F will be the electromagnetic field tensor. From the principle of stationary action, the Yang–Mills equations follow. They are
- [math]\displaystyle{ \mathrm{d}F = 0, \quad \mathrm{d}{*F} = 0. }[/math]
The first of these is an identity, because dF = d2A = 0, but the second is a second-order partial differential equation for the connection A, and if the Minkowski current vector does not vanish, the zero on the rhs. of the second equation is replaced by [math]\displaystyle{ \mathbf J }[/math]. But notice how similar these equations are; they differ by a Hodge star. Thus a solution to the simpler first order (non-linear) equation
- [math]\displaystyle{ {*F} = \pm F\, }[/math]
is automatically also a solution of the Yang–Mills equation. This simplification occurs on 4 manifolds with :[math]\displaystyle{ s=1 }[/math] so that [math]\displaystyle{ *^2=+1 }[/math] on 2-forms. Such solutions usually exist, although their precise character depends on the dimension and topology of the base space M, the principal bundle P, and the gauge group G.
In nonabelian Yang–Mills theories, [math]\displaystyle{ DF=0 }[/math] and [math]\displaystyle{ D*F=0 }[/math] where D is the exterior covariant derivative. Furthermore, the Bianchi identity
- [math]\displaystyle{ DF=dF+A\wedge F-F\wedge A=d(dA+A\wedge A)+A\wedge (dA+A\wedge A)-(dA + A\wedge A)\wedge A=0 }[/math]
is satisfied.
In quantum field theory, an instanton is a topologically nontrivial field configuration in four-dimensional Euclidean space (considered as the Wick rotation of Minkowski spacetime). Specifically, it refers to a Yang–Mills gauge field A which approaches pure gauge at spatial infinity. This means the field strength
- [math]\displaystyle{ \mathbf{F}=d\mathbf{A}+\mathbf{A}\wedge\mathbf{A} }[/math]
vanishes at infinity. The name instanton derives from the fact that these fields are localized in space and (Euclidean) time – in other words, at a specific instant.
The case of instantons on the two-dimensional space may be easier to visualise because it admits the simplest case of the gauge group, namely U(1), that is an abelian group. In this case the field A can be visualised as simply a vector field. An instanton is a configuration where, for example, the arrows point away from a central point (i.e., a "hedgehog" state). In Euclidean four dimensions, [math]\displaystyle{ \mathbb{R}^4 }[/math], abelian instantons are impossible.
The field configuration of an instanton is very different from that of the vacuum. Because of this instantons cannot be studied by using Feynman diagrams, which only include perturbative effects. Instantons are fundamentally non-perturbative.
The Yang–Mills energy is given by
- [math]\displaystyle{ \frac{1}{2}\int_{\mathbb{R}^4} \operatorname{Tr}[*\mathbf{F}\wedge \mathbf{F}] }[/math]
where ∗ is the Hodge dual. If we insist that the solutions to the Yang–Mills equations have finite energy, then the curvature of the solution at infinity (taken as a limit) has to be zero. This means that the Chern–Simons invariant can be defined at the 3-space boundary. This is equivalent, via Stokes' theorem, to taking the integral
- [math]\displaystyle{ \int_{\mathbb{R}^4}\operatorname{Tr}[\mathbf{F}\wedge\mathbf{F}]. }[/math]
This is a homotopy invariant and it tells us which homotopy class the instanton belongs to.
Since the integral of a nonnegative integrand is always nonnegative,
- [math]\displaystyle{ 0\leq\frac{1}{2}\int_{\mathbb{R}^4}\operatorname{Tr}[(*\mathbf{F}+e^{-i\theta}\mathbf{F})\wedge(\mathbf{F}+e^{i\theta}*\mathbf{F})] =\int_{\mathbb{R}^4}\operatorname{Tr}[*\mathbf{F}\wedge\mathbf{F}+\cos\theta \mathbf{F}\wedge\mathbf{F}] }[/math]
for all real θ. So, this means
- [math]\displaystyle{ \frac{1}{2}\int_{\mathbb{R}^4}\operatorname{Tr}[*\mathbf{F}\wedge\mathbf{F}]\geq\frac{1}{2}\left|\int_{\mathbb{R}^4}\operatorname{Tr}[\mathbf{F}\wedge\mathbf{F}]\right|. }[/math]
If this bound is saturated, then the solution is a BPS state. For such states, either ∗F = F or ∗F = − F depending on the sign of the homotopy invariant.
In the Standard Model instantons are expected to be present both in the electroweak sector and the chromodynamic sector, however, their existence has not yet been experimentally confirmed.[12] Instanton effects are important in understanding the formation of condensates in the vacuum of quantum chromodynamics (QCD) and in explaining the mass of the so-called 'eta-prime particle', a Goldstone-boson[note 3] which has acquired mass through the axial current anomaly of QCD. Note that there is sometimes also a corresponding soliton in a theory with one additional space dimension. Recent research on instantons links them to topics such as D-branes and Black holes and, of course, the vacuum structure of QCD. For example, in oriented string theories, a Dp brane is a gauge theory instanton in the world volume (p + 5)-dimensional U(N) gauge theory on a stack of N D(p + 4)-branes.
Various numbers of dimensions
Instantons play a central role in the nonperturbative dynamics of gauge theories. The kind of physical excitation that yields an instanton depends on the number of dimensions of the spacetime, but, surprisingly, the formalism for dealing with these instantons is relatively dimension-independent.
In 4-dimensional gauge theories, as described in the previous section, instantons are gauge bundles with a nontrivial four-form characteristic class. If the gauge symmetry is a unitary group or special unitary group then this characteristic class is the second Chern class, which vanishes in the case of the gauge group U(1). If the gauge symmetry is an orthogonal group then this class is the first Pontrjagin class.
In 3-dimensional gauge theories with Higgs fields, 't Hooft–Polyakov monopoles play the role of instantons. In his 1977 paper Quark Confinement and Topology of Gauge Groups, Alexander Polyakov demonstrated that instanton effects in 3-dimensional QED coupled to a scalar field lead to a mass for the photon.
In 2-dimensional abelian gauge theories worldsheet instantons are magnetic vortices. They are responsible for many nonperturbative effects in string theory, playing a central role in mirror symmetry.
In 1-dimensional quantum mechanics, instantons describe tunneling, which is invisible in perturbation theory.
4d supersymmetric gauge theories
Supersymmetric gauge theories often obey nonrenormalization theorems, which restrict the kinds of quantum corrections which are allowed. Many of these theorems only apply to corrections calculable in perturbation theory and so instantons, which are not seen in perturbation theory, provide the only corrections to these quantities.
Field theoretic techniques for instanton calculations in supersymmetric theories were extensively studied in the 1980s by multiple authors. Because supersymmetry guarantees the cancellation of fermionic vs. bosonic non-zero modes in the instanton background, the involved 't Hooft computation of the instanton saddle point reduces to an integration over zero modes.
In N = 1 supersymmetric gauge theories instantons can modify the superpotential, sometimes lifting all of the vacua. In 1984, Ian Affleck, Michael Dine and Nathan Seiberg calculated the instanton corrections to the superpotential in their paper Dynamical Supersymmetry Breaking in Supersymmetric QCD. More precisely, they were only able to perform the calculation when the theory contains one less flavor of chiral matter than the number of colors in the special unitary gauge group, because in the presence of fewer flavors an unbroken nonabelian gauge symmetry leads to an infrared divergence and in the case of more flavors the contribution is equal to zero. For this special choice of chiral matter, the vacuum expectation values of the matter scalar fields can be chosen to completely break the gauge symmetry at weak coupling, allowing a reliable semi-classical saddle point calculation to proceed. By then considering perturbations by various mass terms they were able to calculate the superpotential in the presence of arbitrary numbers of colors and flavors, valid even when the theory is no longer weakly coupled.
In N = 2 supersymmetric gauge theories the superpotential receives no quantum corrections. However the correction to the metric of the moduli space of vacua from instantons was calculated in a series of papers. First, the one instanton correction was calculated by Nathan Seiberg in Supersymmetry and Nonperturbative beta Functions. The full set of corrections for SU(2) Yang–Mills theory was calculated by Nathan Seiberg and Edward Witten in "Electric – magnetic duality, monopole condensation, and confinement in N=2 supersymmetric Yang–Mills theory," in the process creating a subject that is today known as Seiberg–Witten theory. They extended their calculation to SU(2) gauge theories with fundamental matter in Monopoles, duality and chiral symmetry breaking in N=2 supersymmetric QCD. These results were later extended for various gauge groups and matter contents, and the direct gauge theory derivation was also obtained in most cases. For gauge theories with gauge group U(N) the Seiberg–Witten geometry has been derived from gauge theory using Nekrasov partition functions in 2003 by Nikita Nekrasov and Andrei Okounkov and independently by Hiraku Nakajima and Kota Yoshioka.
In N = 4 supersymmetric gauge theories the instantons do not lead to quantum corrections for the metric on the moduli space of vacua.
Explicit solutions on ℝ4
An ansatz provided by Corrigan and Fairlie provides a solution to the anti-self dual Yang–Mills equations with gauge group SU(2) from any harmonic function on [math]\displaystyle{ \mathbb{R}^4 }[/math].[13][14] The ansatz gives explicit expressions for the gauge field and can be used to construct solutions with arbitrarily large instanton number.
Defining the antisymmetric [math]\displaystyle{ \mathfrak{su}(2) }[/math]-valued objects [math]\displaystyle{ \sigma_{\mu\nu} }[/math] as [math]\displaystyle{ \sigma_{ij} = \epsilon_{ijk}T_k\, , \sigma_{i4} = -\sigma_{4i} = T_i, }[/math] where Greek indices run from 1 to 4, Latin indices run from 1 to 3, and [math]\displaystyle{ T_i }[/math] is a basis of [math]\displaystyle{ \mathfrak{su}(2) }[/math] satisfying [math]\displaystyle{ [T_i, T_j] = -\epsilon_{ijk}T_k }[/math]. Then [math]\displaystyle{ A_\mu = \sigma_{\mu\nu}\frac{\partial_\nu \rho}{\rho} = \sigma_{\mu\nu}\partial_\nu \log(\rho) }[/math] is a solution as long as [math]\displaystyle{ \rho: \mathbb{R}^4 \rightarrow \mathbb{R} }[/math] is harmonic.
In four dimensions, the fundamental solution to Laplace's equation is [math]\displaystyle{ |x - y|^{-2} }[/math] for any fixed [math]\displaystyle{ y }[/math]. Superposing [math]\displaystyle{ N+1 }[/math] of these gives [math]\displaystyle{ N }[/math]-soliton solutions of the form [math]\displaystyle{ \rho(x) = \sum_{p=1}^N \frac{\lambda_p}{|x - x_p|^2}. }[/math] All solutions of instanton number 1 or 2 are of this form, but for larger instanton number there are solutions not of this form.
See also
- Physics:Instanton fluid – Non-perturbative path integral approximation
- Physics:Caloron – Finite temperature instanton
- Biography:Sidney Coleman – American physicist (1937–2007)
- Gravitational instanton – Four-dimensional complete Riemannian manifold satisfying the vacuum Einstein equations
- Chemistry:Semiclassical transition state theory – Chemical reaction rate theory
- Yang–Mills equations – Partial differential equations whose solutions are instantons
- Gauge theory (mathematics) – Study of vector bundles, principal bundles, and fibre bundles
References and notes
- Notes
- ↑ Because this projection is conformal, the curves intersect each other orthogonally (in the yellow points) as in 4D. All curves are circles: the curves that intersect <0,0,0,1> have infinite radius (= straight line).
- ↑ See also: Non-abelian gauge theory
- ↑ See also: Pseudo-Goldstone boson
- Citations
- ↑ Instantons in Gauge Theories. Edited by Mikhail A. Shifman. World Scientific, 1994.
- ↑ Interactions Between Charged Particles in a Magnetic Field. By Hrachya Nersisyan, Christian Toepffer, Günter Zwicknagel. Springer, Apr 19, 2007. Pg 23
- ↑ Large-Order Behaviour of Perturbation Theory. Edited by J.C. Le Guillou, J. Zinn-Justin. Elsevier, Dec 2, 2012. Pg. 170.
- ↑ Jump up to: 4.0 4.1 Vaĭnshteĭn, A. I.; Zakharov, Valentin I.; Novikov, Viktor A.; Shifman, Mikhail A. (1982-04-30). "ABC of instantons" (in en). Soviet Physics Uspekhi 25 (4): 195. doi:10.1070/PU1982v025n04ABEH004533. ISSN 0038-5670. https://iopscience.iop.org/article/10.1070/PU1982v025n04ABEH004533/meta.
- ↑ "Yang-Mills instanton in nLab". https://ncatlab.org/nlab/show/Yang-Mills+instanton.
- ↑ See, for instance, Nigel Hitchin's paper "Self-Duality Equations on Riemann Surface".
- ↑ H.J.W. Müller-Kirsten, Introduction to Quantum Mechanics: Schrödinger Equation and Path Integral, 2nd ed. (World Scientific, 2012), ISBN:978-981-4397-73-5; formula (18.175b), p. 525.
- ↑ H.J.W. Müller-Kirsten, Introduction to Quantum Mechanics: Schrödinger Equation and Path Integral, 2nd ed., World Scientific, 2012, ISBN:978-981-4397-73-5.
- ↑ Jump up to: 9.0 9.1 Harald J.W. Müller-Kirsten, Introduction to Quantum Mechanics: Schrödinger Equation and Path Integral, 2nd ed., World Scientific (Singapore, 2012).
- ↑ Liang, Jiu-Qing; Müller-Kirsten, H.J.W.; Tchrakian, D.H. (1992). "Solitons, bounces and sphalerons on a circle". Physics Letters B (Elsevier BV) 282 (1–2): 105–110. doi:10.1016/0370-2693(92)90486-n. ISSN 0370-2693. Bibcode: 1992PhLB..282..105L.
- ↑ Bender, Carl M.; Wu, Tai Tsun (1973-03-15). "Anharmonic Oscillator. II. A Study of Perturbation Theory in Large Order". Physical Review D (American Physical Society (APS)) 7 (6): 1620–1636. doi:10.1103/physrevd.7.1620. ISSN 0556-2821. Bibcode: 1973PhRvD...7.1620B.
- ↑ Amoroso, Simone; Kar, Deepak; Schott, Matthias (2021). "How to discover QCD Instantons at the LHC". The European Physical Journal C 81 (7): 624. doi:10.1140/epjc/s10052-021-09412-1. Bibcode: 2021EPJC...81..624A.
- ↑ Corrigan, E.; Fairlie, D.B. (March 1977). "Scalar field theory and exact solutions to a classical SU (2) gauge theory". Physics Letters B 67 (1): 69–71. doi:10.1016/0370-2693(77)90808-5.
- ↑ Dunajski, Maciej (2010). Solitons, instantons, and twistors. Oxford: Oxford University Press. p. 123. ISBN 9780198570639.
- General
- Instantons in Gauge Theories, a compilation of articles on instantons, edited by Mikhail A. Shifman, doi:10.1142/2281
- Solitons and Instantons, R. Rajaraman (Amsterdam: North Holland, 1987), ISBN:0-444-87047-4
- The Uses of Instantons, by Sidney Coleman in Proc. Int. School of Subnuclear Physics, (Erice, 1977); and in Aspects of Symmetry p. 265, Sidney Coleman, Cambridge University Press, 1985, ISBN:0-521-31827-0; and in Instantons in Gauge Theories
- Solitons, Instantons and Twistors. M. Dunajski, Oxford University Press. ISBN:978-0-19-857063-9.
- The Geometry of Four-Manifolds, S.K. Donaldson, P.B. Kronheimer, Oxford University Press, 1990, ISBN:0-19-853553-8.
External links
 |