E8 (mathematics)
| Algebraic structure → Group theory Group theory |
|---|
 |
| Group theory → Lie groups Lie groups |
|---|
 |
In mathematics, E8 is any of several closely related exceptional simple Lie groups, linear algebraic groups or Lie algebras of dimension 248; the same notation is used for the corresponding root lattice, which has rank 8. The designation E8 comes from the Cartan–Killing classification of the complex simple Lie algebras, which fall into four infinite series labeled An, Bn, Cn, Dn, and five exceptional cases labeled G2, F4, E6, E7, and E8. The E8 algebra is the largest and most complicated of these exceptional cases.
Basic description
The Lie group E8 has dimension 248. Its rank, which is the dimension of its maximal torus, is eight.
Therefore, the vectors of the root system are in eight-dimensional Euclidean space: they are described explicitly later in this article. The Weyl group of E8, which is the group of symmetries of the maximal torus which are induced by conjugations in the whole group, has order 214 35 52 7 = 696729600.
The compact group E8 is unique among simple compact Lie groups in that its non-trivial representation of smallest dimension is the adjoint representation (of dimension 248) acting on the Lie algebra E8 itself; it is also the unique one which has the following four properties: trivial center, compact, simply connected, and simply laced (all roots have the same length).
There is a Lie algebra Ek for every integer k ≥ 3. The largest value of k for which Ek is finite-dimensional is k = 8, that is, Ek is infinite-dimensional for any k > 8.
Real and complex forms
There is a unique complex Lie algebra of type E8, corresponding to a complex group of complex dimension 248. The complex Lie group E8 of complex dimension 248 can be considered as a simple real Lie group of real dimension 496. This is simply connected, has maximal compact subgroup the compact form (see below) of E8, and has an outer automorphism group of order 2 generated by complex conjugation.
As well as the complex Lie group of type E8, there are three real forms of the Lie algebra, three real forms of the group with trivial center (two of which have non-algebraic double covers, giving two further real forms), all of real dimension 248, as follows:
- The compact form (which is usually the one meant if no other information is given), which is simply connected and has trivial outer automorphism group.
- The split form, EVIII (or E8(8)), which has maximal compact subgroup Spin(16)/(Z/2Z), fundamental group of order 2 (implying that it has a double cover, which is a simply connected Lie real group but is not algebraic, see below) and has trivial outer automorphism group.
- EIX (or E8(−24)), which has maximal compact subgroup E7×SU(2)/(−1,−1), fundamental group of order 2 (again implying a double cover, which is not algebraic) and has trivial outer automorphism group.
For a complete list of real forms of simple Lie algebras, see the list of simple Lie groups.
E8 as an algebraic group
By means of a Chevalley basis for the Lie algebra, one can define E8 as a linear algebraic group over the integers and, consequently, over any commutative ring and in particular over any field: this defines the so-called split (sometimes also known as “untwisted”) form of E8. Over an algebraically closed field, this is the only form; however, over other fields, there are often many other forms, or “twists” of E8, which are classified in the general framework of Galois cohomology (over a perfect field k) by the set H1(k,Aut(E8)) which, because the Dynkin diagram of E8 (see below) has no automorphisms, coincides with H1(k,E8).[1]
Over R, the real connected component of the identity of these algebraically twisted forms of E8 coincide with the three real Lie groups mentioned above, but with a subtlety concerning the fundamental group: all forms of E8 are simply connected in the sense of algebraic geometry, meaning that they admit no non-trivial algebraic coverings; the non-compact and simply connected real Lie group forms of E8 are therefore not algebraic and admit no faithful finite-dimensional representations.
Over finite fields, the Lang–Steinberg theorem implies that H1(k,E8)=0, meaning that E8 has no twisted forms: see below.
The characters of finite dimensional representations of the real and complex Lie algebras and Lie groups are all given by the Weyl character formula. The dimensions of the smallest irreducible representations are (sequence A121732 in the OEIS):
- 1, 248, 3875, 27000, 30380, 147250, 779247, 1763125, 2450240, 4096000, 4881384, 6696000, 26411008, 70680000, 76271625, 79143000, 146325270, 203205000, 281545875, 301694976, 344452500, 820260000, 1094951000, 2172667860, 2275896000, 2642777280, 2903770000, 3929713760, 4076399250, 4825673125, 6899079264, 8634368000 (twice), 12692520960...
The 248-dimensional representation is the adjoint representation. There are two non-isomorphic irreducible representations of dimension 8634368000 (it is not unique; however, the next integer with this property is 175898504162692612600853299200000 (sequence A181746 in the OEIS)). The fundamental representations are those with dimensions 3875, 6696000, 6899079264, 146325270, 2450240, 30380, 248 and 147250 (corresponding to the eight nodes in the Dynkin diagram in the order chosen for the Cartan matrix below, i.e., the nodes are read in the seven-node chain first, with the last node being connected to the third).
The coefficients of the character formulas for infinite dimensional irreducible representations of E8 depend on some large square matrices consisting of polynomials, the Lusztig–Vogan polynomials, an analogue of Kazhdan–Lusztig polynomials introduced for reductive groups in general by George Lusztig and David Kazhdan (1983). The values at 1 of the Lusztig–Vogan polynomials give the coefficients of the matrices relating the standard representations (whose characters are easy to describe) with the irreducible representations.
These matrices were computed after four years of collaboration by a group of 18 mathematicians and computer scientists, led by Jeffrey Adams, with much of the programming done by Fokko du Cloux. The most difficult case (for exceptional groups) is the split real form of E8 (see above), where the largest matrix is of size 453060×453060. The Lusztig–Vogan polynomials for all other exceptional simple groups have been known for some time; the calculation for the split form of E8 is far longer than any other case. The announcement of the result in March 2007 received extraordinary attention from the media (see the external links), to the surprise of the mathematicians working on it.
The representations of the E8 groups over finite fields are given by Deligne–Lusztig theory.
Constructions
One can construct the (compact form of the) E8 group as the automorphism group of the corresponding e8 Lie algebra. This algebra has a 120-dimensional subalgebra so(16) generated by Jij as well as 128 new generators Qa that transform as a Weyl–Majorana spinor of spin(16). These statements determine the commutators
as well as
while the remaining commutators (not anticommutators!) between the spinor generators are defined as
It is then possible to check that the Jacobi identity is satisfied.
Geometry
The compact real form of E8 is the isometry group of the 128-dimensional exceptional compact Riemannian symmetric space EVIII (in Cartan's classification). It is known informally as the "octooctonionic projective plane" because it can be built using an algebra that is the tensor product of the octonions with themselves, and is also known as a Rosenfeld projective plane, though it does not obey the usual axioms of a projective plane. This can be seen systematically using a construction known as the magic square, due to Hans Freudenthal and Jacques Tits (Landsberg Manivel).
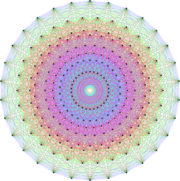
E8 root system












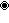

- u = (1, φ, 0, −1, φ, 0,0,0)
- v = (φ, 0, 1, φ, 0, −1,0,0)
- w = (0, 1, φ, 0, −1, φ,0,0)
- 4 points at the origin
- 2 icosahedrons
- 2 dodecahedrons
- 4 icosahedrons
- 1 icosadodecahedron
- 2 dodecahedrons
- 2 icosahedrons
- 1 icosadodecahedron
A root system of rank r is a particular finite configuration of vectors, called roots, which span an r-dimensional Euclidean space and satisfy certain geometrical properties. In particular, the root system must be invariant under reflection through the hyperplane perpendicular to any root.
The E8 root system is a rank 8 root system containing 240 root vectors spanning R8. It is irreducible in the sense that it cannot be built from root systems of smaller rank. All the root vectors in E8 have the same length. It is convenient for a number of purposes to normalize them to have length √2. These 240 vectors are the vertices of a semi-regular polytope discovered by Thorold Gosset in 1900, sometimes known as the 421 polytope.
Construction
In the so-called even coordinate system, E8 is given as the set of all vectors in R8 with length squared equal to 2 such that coordinates are either all integers or all half-integers and the sum of the coordinates is even.
Explicitly, there are 112 roots with integer entries obtained from
by taking an arbitrary combination of signs and an arbitrary permutation of coordinates, and 128 roots with half-integer entries obtained from
by taking an even number of minus signs (or, equivalently, requiring that the sum of all the eight coordinates be even). There are 240 roots in all.

The 112 roots with integer entries form a D8 root system. The E8 root system also contains a copy of A8 (which has 72 roots) as well as E6 and E7 (in fact, the latter two are usually defined as subsets of E8).
In the odd coordinate system, E8 is given by taking the roots in the even coordinate system and changing the sign of any one coordinate. The roots with integer entries are the same while those with half-integer entries have an odd number of minus signs rather than an even number.
Dynkin diagram
The Dynkin diagram for E8 is given by ![]() .
.
This diagram gives a concise visual summary of the root structure. Each node of this diagram represents a simple root. A line joining two simple roots indicates that they are at an angle of 120° to each other. Two simple roots which are not joined by a line are orthogonal.
Cartan matrix
The Cartan matrix of a rank r root system is an r × r matrix whose entries are derived from the simple roots. Specifically, the entries of the Cartan matrix are given by
where ( , ) is the Euclidean inner product and αi are the simple roots. The entries are independent of the choice of simple roots (up to ordering).
The Cartan matrix for E8 is given by
The determinant of this matrix is equal to 1.
Simple roots

A set of simple roots for a root system Φ is a set of roots that form a basis for the Euclidean space spanned by Φ with the special property that each root has components with respect to this basis that are either all nonnegative or all nonpositive.
Given the E8 Cartan matrix (above) and a Dynkin diagram node ordering of: ![]()
One choice of simple roots is given by the rows of the following matrix:
With this numbering of nodes in the Dynkin diagram, the highest root in the root system has Coxeter labels (2, 3, 4, 5, 6, 4, 2, 3). Using this representation of the simple roots, the lowest root is given by
The only simple root that can be added to the lowest root to obtain another root is the one corresponding to node 1 in this labeling of the Dynkin diagram — as is to be expected from the affine Dynkin diagram for . The Hasse diagram to the right enumerates the 120 roots of positive height relative to any particular choice of simple roots consistent with this node numbering.
Note that the Hasse diagram does not represent the full Lie algebra, or even the full root system. The 120 roots of negative height relative to the same set of simple roots can be adequately represented by a second copy of the Hasse diagram with the arrows reversed; but it is less straightforward to connect these two diagrams via a basis for the eight-dimensional Cartan subalgebra. In the notation of the exposition of Chevalley generators and Serre relations: Insofar as an arrow represents the Lie bracket by the generator associated with a simple root, each root in the height -1 layer of the reversed Hasse diagram must correspond to some and can have only one upward arrow, connected to a node in the height 0 layer representing the element of the Cartan subalgebra given by . But the upward arrows from the height 0 layer must then represent , where is (the transpose of) the Cartan matrix. One could draw multiple upward arrows from each associated with all for which is nonzero; but this neither captures the numerical entries in the Cartan matrix nor reflects the fact that each only has nonzero Lie bracket with one degree of freedom in the Cartan subalgebra (just not the same degree of freedom as ).
More fundamentally, this organization implies that the span of the generators designated as "the" Cartan subalgebra is somehow inherently special, when in most applications, any mutually commuting set of eight of the 248 Lie algebra generators (of which there are many!) — or any eight linearly independent, mutually commuting Lie derivations on any manifold with E8 structure — would have served just as well. Once a Cartan subalgebra has been selected (or defined a priori, as in the case of a lattice), a basis of "Cartan generators" (the among the Chevalley generators) and a root system are a useful way to describe structure relative to this subalgebra. But the root system map is not the Lie algebra (let alone group!) territory. Given a set of Chevalley generators, most degrees of freedom in a Lie algebra and their sparse Lie brackets with can be represented schematically as circles and arrows, but this simply breaks down on the chosen Cartan subalgebra. Such are the hazards of schematic visual representations of mathematical structures.
Weyl group
The Weyl group of E8 is of order 696729600, and can be described as O+8(2): it is of the form 2.G.2 (that is, a stem extension by the cyclic group of order 2 of an extension of the cyclic group of order 2 by a group G) where G is the unique simple group of order 174182400 (which can be described as PSΩ8+(2)).[3]
E8 root lattice
The integral span of the E8 root system forms a lattice in R8 naturally called the E8 root lattice. This lattice is rather remarkable in that it is the only (nontrivial) even, unimodular lattice with rank less than 16.
Simple subalgebras of E8

The Lie algebra E8 contains as subalgebras all the exceptional Lie algebras as well as many other important Lie algebras in mathematics and physics. The height of the Lie algebra on the diagram approximately corresponds to the rank of the algebra. A line from an algebra down to a lower algebra indicates that the lower algebra is a subalgebra of the higher algebra.
Chevalley groups of type E8
(Chevalley 1955) showed that the points of the (split) algebraic group E8 (see above) over a finite field with q elements form a finite Chevalley group, generally written E8(q), which is simple for any q,[4][5] and constitutes one of the infinite families addressed by the classification of finite simple groups. Its number of elements is given by the formula (sequence A008868 in the OEIS):
The first term in this sequence, the order of E8(2), namely 337804753143634806261388190614085595079991692242467651576160959909068800000 ≈ 3.38×1074, is already larger than the size of the Monster group. This group E8(2) is the last one described (but without its character table) in the ATLAS of Finite Groups.[6]
The Schur multiplier of E8(q) is trivial, and its outer automorphism group is that of field automorphisms (i.e., cyclic of order f if q=pf where p is prime).
(Lusztig 1979) described the unipotent representations of finite groups of type E8.
Subgroups, subalgebras, and extensions
The smaller exceptional groups E7 and E6 sit inside E8. In the compact group, both E6×SU(3)/(Z/3Z) and E7×SU(2)/(+1,−1) are maximal subgroups of E8.

The 248-dimensional adjoint representation of E8 may be considered in terms of its restricted representation to the first of these subgroups. It transforms under E6×SU(3) as a sum of tensor product representations, which may be labelled as a pair of dimensions as (78,1) + (1,8) + (27,3) + (27,3). (Since the maximal subgroup is actually the quotient of this group product by a finite group, these notations may strictly be taken as indicating the infinitesimal (Lie algebra) representations.) Since the adjoint representation can be described by the roots together with the generators in the Cartan subalgebra, we may choose a particular E6 root system within E8 and decompose the sum representation relative to this E6. In this description,
- (78,1), a copy of , consists of the 72 roots with (−1⁄2,−1⁄2,−1⁄2), (0,0,0), or (1⁄2,1⁄2,1⁄2) in the last three dimensions, together with five Cartan generators corresponding to the first five dimensions and one Cartan generator corresponding to an equally weighted sum of the last three Cartan generators of the E8 system;
- (1,8), a copy of , consists of the six roots with permutations of (0,1,−1) in the last three dimensions, together with two Cartan generators corresponding to the two trace-free combinations of the last three Cartan generators of the E8 system;
- (27,3) consists of all roots with permutations of (-1,0,0), (−1⁄2,1⁄2,1⁄2), or (0,1,1) in the last three dimensions; and
- (27,3) consists of all roots with permutations of (1,0,0), (1⁄2,−1⁄2,−1⁄2), or (0,-1,-1) in the last three dimensions.
The 248-dimensional adjoint representation of E8, when similarly restricted to the second maximal subgroup, transforms under E7×SU(2) as: (133,1) + (1,3) + (56,2). We may again see the decomposition by looking at the roots together with the generators in the Cartan subalgebra. In this description,
- (133,1), a copy of , consists of the 126 roots with (−1,−1), (−1⁄2,−1⁄2), (0,0), (1⁄2,1⁄2), or (1,1) in the last two dimensions, together with six Cartan generators corresponding to the first six dimensions and one Cartan generator corresponding to an equally weighted sum of the last two Cartan generators of the E8 system;
- (1,3), a copy of , consists of the two roots (0,0,0,0,0,0,1,−1), (0,0,0,0,0,0,−1,1), together with one Cartan generator corresponding to the trace-free combination of the last two Cartan generators of the E8 system; and
- (56,2) consists of all roots with permutations of (0,-1), (1⁄2,−1⁄2), or (1,0) in the last two dimensions.
The connection between these two descriptions is given by the graded exceptional Lie algebra constructions of J. Tits and B. N. Allison. Any 27-dimensional representation of E6 can be equipped with a non-associative (but strictly power-associative) Jordan product operation to form an Albert algebra (an important exceptional case in algebraic constructions). The Kantor–Koecher–Tits construction applied to this Albert algebra recovers the 78-dimensional as the reduced structure algebra of the Albert algebra. This , together with the 27 and 27 representations and the grade operator (the element of the Cartan subalgebra with weight -1 on the 27, +1 on the 27, and 0 on the 78), forms an 3-graded Lie algebra. A complete exposition of this construction may be found in standard texts on Jordan algebras such as Jacobson 1968 or McCrimmon 2004.
Starting this 3-graded Lie algebra construction with any particular 27-dimensional representation, embedded within , of any particular E6 subgroup of E8 produces the corresponding subalgebra. The particular in the E7×SU(2) decomposition given above corresponds to choosing the 27 consisting of all roots with (1,0,0), (1⁄2,-1⁄2,-1⁄2), or (0,-1,-1) in the last three dimensions (in order), with the grade operator having weight (-1,1⁄2,1⁄2) in these dimensions; or equivalently to choosing the "27" consisting of all roots with (-1,0,0), (−1⁄2,1⁄2,1⁄2), or (0,1,1) in the last three dimensions (in order), with the grade operator having weight (1,-1⁄2,-1⁄2) in these dimensions. Note that there is nothing special about this choice of dimensions — the within which the root system is embedded is not the set of eight independent but non-orthogonal axes corresponding to the simple roots, and any three dimensions will do — and there are also constructions using other equivalent groupings of roots. What matters is that the kernel of the Lie bracket with the generator chosen as the "grade operator" be an subalgebra (plus a central associated with the grade operator itself and the remaining generator of the Cartan subalgebra), not , , , etc.
(In the simple Lie algebra case, the sign of the grade of the 27 versus the 27 representation is a matter of convention, as is the scale of the grading. However, choosing -1 as the grade of the 27-dimensional "vector" representation is consistent with an extension of the 3-graded algebra to higher positive grades via the exterior algebra over the 27 "covector" representation. The "vector" representation then lies, not in this nonnegative-graded exterior algebra, but in the graded algebra of derivations over the exterior algebra; the 78-dimensional is the grade 0 subalgebra (a subalgebra of the inner derivations by "vector-valued 1-forms") of this graded algebra of derivations. For details on how this asymmetric structure works starting from a general 3-graded algebra, see references at Frölicher–Nijenhuis bracket. The relevance of this observation to E8 is simply that E7 and E8 are their own clusters of structures, distinguished as exceptional simple Lie groups/algebras, and that any particular reconstruction of them using representations of their subgroups/subalgebras will have extensions beyond the motivating case. Varying conventions of sign, scale, and conjugate relationship in the literature are due not just to inaccuracies but also to the directions in which the authors seek to extend their constructions.)
The distinguished in the E7×SU(2) decomposition above is then given by the subalgebra of that commutes with the grade operator (which lies in the Cartan subalgebra of this ). Of the four remaining roots in the , two are of grade 1⁄2 and two are of grade -1⁄2. In the convention where the 27 of E6 used to construct the has grade -1 and the 27 has grade +1, the other two 27's have grade +1⁄2 and the other two 27's have grade -1⁄2, as is apparent from permuting the values of the last three roots in the description above. Grouping these 4×(1+27)=112 generators to form the grade +1⁄2 and -1⁄2 subspaces of (relative to the original choice of grade operator within ), each subspace may be given a quite particular non-associative (nor even power-associative) product operation, resulting in two copies of Brown's 56-dimensional structurable algebra. Allison's 5-graded Lie algebra construction based on this structurable algebra recovers the original . (Allison's 5-grading differs from the above by a factor -2.) Grouping these generators differently, based on their weights relative to the Cartan generator of the orthogonal to , gives two 56-dimensional subspaces which each carry the lowest-dimensional non-trivial irreducible representation of E7. Either of these may be combined with the Cartan generator to form a 57-dimensional Heisenberg algebra, and adjoining this to produces the (non-simple) Lie algebra E7½ described by Landsberg and Manivel.
From the perspective in which the 27-dimensional grade -1 subspace of (relative to a choice of grade operator) plays the role of "vector" representation of E6 and the 27 with roots opposite it plays the role of "covector" representation, it is natural to look for "spinor" representations in the grade +1⁄2 and -1⁄2 subspaces, or in some other combination of the (27,3) and (27,3) representations of E6×SU(3), and to attempt to relate these to geometrical spinors in the Clifford algebra sense as employed in quantum field theory. Variations on this idea are common in the physics literature. See Distler and Garibaldi 2009 for discussion of the mathematical obstacles to constructing a chiral gauge theory based on E8. The structure of relative to its subalgebra, together with the conventional scaling of elements of the Cartan subalgebra, invites extensions by geometric analogy but does not necessarily imply a relationship to low-dimensional geometry or low-energy physics. The same may be said of connections to Jordan and Heisenberg algebras, whose historical origins are intertwined with the development of quantum mechanics. Not every visual representation evocative of a tobacco pipe will hold tobacco.
The finite quasisimple groups that can embed in (the compact form of) E8 were found by (Griess Ryba).
The Dempwolff group is a subgroup of (the compact form of) E8. It is contained in the Thompson sporadic group, which acts on the underlying vector space of the Lie group E8 but does not preserve the Lie bracket. The Thompson group fixes a lattice and does preserve the Lie bracket of this lattice mod 3, giving an embedding of the Thompson group into E8(F3).
The embeddings of the maximal subgroups of E8 up to dimension 248 are shown to the right.
Applications
The E8 Lie group has applications in theoretical physics and especially in string theory and supergravity. E8×E8 is the gauge group of one of the two types of heterotic string and is one of two anomaly-free gauge groups that can be coupled to the N = 1 supergravity in ten dimensions. E8 is the U-duality group of supergravity on an eight-torus (in its split form).
One way to incorporate the standard model of particle physics into heterotic string theory is the symmetry breaking of E8 to its maximal subalgebra SU(3)×E6.
In 1982, Michael Freedman used the E8 lattice to construct an example of a topological 4-manifold, the E8 manifold, which has no smooth structure.
Antony Garrett Lisi's incomplete "An Exceptionally Simple Theory of Everything" attempts to describe all known fundamental interactions in physics as part of the E8 Lie algebra.[7][8]
R. Coldea, D. A. Tennant, and E. M. Wheeler et al. (2010) reported an experiment where the electron spins of a cobalt-niobium crystal exhibited, under certain conditions, two of the eight peaks related to E8 that were predicted by (Zamolodchikov 1989).[9][10]
History
Wilhelm Killing (1888a, 1888b, 1889, 1890) discovered the complex Lie algebra E8 during his classification of simple compact Lie algebras, though he did not prove its existence, which was first shown by Élie Cartan. Cartan determined that a complex simple Lie algebra of type E8 admits three real forms. Each of them gives rise to a simple Lie group of dimension 248, exactly one of which (as for any complex simple Lie algebra) is compact. (Chevalley 1955) introduced algebraic groups and Lie algebras of type E8 over other fields: for example, in the case of finite fields they lead to an infinite family of finite simple groups of Lie type. E8 continues to be an area of active basic research by Atlas of Lie Groups and Representations, which aims to determine the unitary representations of all the Lie groups.[11]
See also
Footnotes
- ↑ Платонов, Владимир П.; Рапинчук, Андрей С. (1991), Алгебраические группы и теория чисел, Наука, ISBN 5-02-014191-7 (English translation: Platonov, Vladimir P.; Rapinchuk, Andrei S. (1994), Algebraic groups and number theory, Academic Press, ISBN 0-12-558180-7), §2.2.4
- ↑ "The 600-Cell (Part 1)". December 16, 2017. https://johncarlosbaez.wordpress.com/2017/12/16/the-600-cell/.
- ↑ Conway, John Horton; Curtis, Robert Turner; Norton, Simon Phillips; Parker, Richard A; Wilson, Robert Arnott (1985), Atlas of Finite Groups: Maximal Subgroups and Ordinary Characters for Simple Groups, Oxford University Press, p. 85, ISBN 0-19-853199-0
- ↑ Carter, Roger W. (1989), Simple Groups of Lie Type, Wiley Classics Library, John Wiley & Sons, ISBN 0-471-50683-4
- ↑ Wilson, Robert A. (2009), The Finite Simple Groups, Graduate Texts in Mathematics, 251, Springer-Verlag, ISBN 978-1-84800-987-5
- ↑ Conway &al, op. cit., p. 235.
- ↑ A. G. Lisi; J. O. Weatherall (2010). "A Geometric Theory of Everything". Scientific American 303 (6): 54–61. doi:10.1038/scientificamerican1210-54. PMID 21141358. Bibcode: 2010SciAm.303f..54L. http://www.scientificamerican.com/article.cfm?id=a-geometric-theory-of-everything.
- ↑ Greg Boustead (2008-11-17). "Garrett Lisi's Exceptional Approach to Everything". SEED Magazine. http://seedmagazine.com/news/2008/11/garrett_lisis_exceptional_appr.php.
- ↑ Shiga, David (2010-01-07). "'Most beautiful' math structure appears in lab for first time" (in en-US). https://www.newscientist.com/article/dn18356-most-beautiful-math-structure-appears-in-lab-for-first-time/.
- ↑ Did a 1-dimensional magnet detect a 248-dimensional Lie algebra?, Notices of the American Mathematical Society, September 2011.
- ↑ "AIM math: Representations of E8". https://aimath.org/E8/.
References
- Adams, J. Frank (1996), Lectures on exceptional Lie groups, Chicago Lectures in Mathematics, University of Chicago Press, ISBN 978-0-226-00526-3, https://books.google.com/books?isbn=0226005275
- Baez, John C. (2002), "The octonions", Bulletin of the American Mathematical Society, New Series 39 (2): 145–205, doi:10.1090/S0273-0979-01-00934-X, https://www.ams.org/bull/2002-39-02/S0273-0979-01-00934-X/home.html
- Chevalley, Claude (1955), "Sur certains groupes simples", The Tohoku Mathematical Journal, Second Series 7 (1–2): 14–66, doi:10.2748/tmj/1178245104, ISSN 0040-8735, http://projecteuclid.org/euclid.tmj/1178245104
- Coldea, R.; Tennant, D. A.; Wheeler, E. M.; Wawrzynska, E.; Prabhakaran, D.; Telling, M.; Habicht, K.; Smeibidl, P. et al. (2010), "Quantum Criticality in an Ising Chain: Experimental Evidence for Emergent E8 Symmetry", Science 327 (5962): 177–180, doi:10.1126/science.1180085, PMID 20056884, Bibcode: 2010Sci...327..177C
- Garibaldi, Skip (2016), "E8, the most exceptional group", Bulletin of the American Mathematical Society 53 (4): 643–671, doi:10.1090/bull/1540
- Griess, Robert L.; Ryba, A. J. E. (1999), "Finite simple groups which projectively embed in an exceptional Lie group are classified!", Bulletin of the American Mathematical Society, New Series 36 (1): 75–93, doi:10.1090/S0273-0979-99-00771-5, https://www.ams.org/bull/1999-36-01/S0273-0979-99-00771-5/home.html
- Killing, Wilhelm (1888a), "Die Zusammensetzung der stetigen endlichen Transformationsgruppen", Mathematische Annalen 31 (2): 252–290, doi:10.1007/BF01211904, http://gdz.sub.uni-goettingen.de/index.php?id=11&PPN=GDZPPN002250810&L=1
- Killing, Wilhelm (1888b), "Die Zusammensetzung der stetigen endlichen Transformationsgruppen", Mathematische Annalen 33 (1): 1–48, doi:10.1007/BF01444109, http://gdz.sub.uni-goettingen.de/index.php?id=11&PPN=GDZPPN002251337&L=1
- Killing, Wilhelm (1889), "Die Zusammensetzung der stetigen endlichen Transformationsgruppen", Mathematische Annalen 34 (1): 57–122, doi:10.1007/BF01446792, http://gdz.sub.uni-goettingen.de/index.php?id=11&PPN=PPN235181684_0034&DMDID=DMDLOG_0009&L=1, retrieved 2013-09-12
- Killing, Wilhelm (1890), "Die Zusammensetzung der stetigen endlichen Transformationsgruppen", Mathematische Annalen 36 (2): 161–189, doi:10.1007/BF01207837, http://gdz.sub.uni-goettingen.de/index.php?id=11&PPN=GDZPPN002252392&L=1
- Landsberg, Joseph M.; Manivel, Laurent (2001), "The projective geometry of Freudenthal's magic square", Journal of Algebra 239 (2): 477–512, doi:10.1006/jabr.2000.8697
- Lusztig, George (1979), "Unipotent representations of a finite Chevalley group of type E8", The Quarterly Journal of Mathematics, Second Series 30 (3): 315–338, doi:10.1093/qmath/30.3.301, ISSN 0033-5606
- Lusztig, George; Vogan, David (1983), "Singularities of closures of K-orbits on flag manifolds", Inventiones Mathematicae (Springer-Verlag) 71 (2): 365–379, doi:10.1007/BF01389103, Bibcode: 1983InMat..71..365L
- Zamolodchikov, A. B. (1989), "Integrals of motion and S-matrix of the (scaled) T=Tc Ising model with magnetic field", International Journal of Modern Physics A 4 (16): 4235–4248, doi:10.1142/S0217751X8900176X, Bibcode: 1989IJMPA...4.4235Z
External links
Lusztig–Vogan polynomial calculation
- Atlas of Lie groups
- Kazhdan–Lusztig–Vogan Polynomials for E8
- Narrative of the Project to compute Kazhdan–Lusztig Polynomials for E8
- American Institute of Mathematics (March 2007), Mathematicians Map E8, http://aimath.org/E8/
- The n-Category Café, a University of Texas blog posting by John Baez on E8.
Other links
- Graphic representation of E8 root system.
- The list of dimensions of irreducible representations of the complex form of E8 is sequence A121732 in the OEIS.
 |