Physics:Brane
| String theory |
|---|
 |
| Fundamental objects |
| Perturbative theory |
| Non-perturbative results |
| Phenomenology |
| Mathematics |
In string theory and related theories such as supergravity theories, a brane is a physical object that generalizes the notion of a zero-dimensional point particle, a one-dimensional string, or a two-dimensional membrane to higher-dimensional objects. Branes are dynamical objects which can propagate through spacetime according to the rules of quantum mechanics. They have mass and can have other attributes such as charge.
Mathematically, branes can be represented within categories, and are studied in pure mathematics for insight into homological mirror symmetry and noncommutative geometry.
p-branes
A point particle is a 0-brane, of dimension zero; a string, named after vibrating musical strings, is a 1-brane; a membrane, named after vibrating membranes such as drumheads, is a 2-brane.[1] The corresponding object of arbitrary dimension p is called a p-brane, a term coined by M. J. Duff et al. in 1988.[2]
A p-brane sweeps out a (p+1)-dimensional volume in spacetime called its worldvolume. Physicists often study fields analogous to the electromagnetic field, which live on the worldvolume of a brane.[3]
D-branes
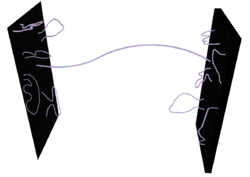
In string theory, a string may be open (forming a segment with two endpoints) or closed (forming a closed loop). D-branes are an important class of branes that arise when one considers open strings. As an open string propagates through spacetime, its endpoints are required to lie on a D-brane. The letter "D" in D-brane refers to the Dirichlet boundary condition, which the D-brane satisfies.[4]
One crucial point about D-branes is that the dynamics on the D-brane worldvolume is described by a gauge theory, a kind of highly symmetric physical theory which is also used to describe the behavior of elementary particles in the standard model of particle physics. This connection has led to important insights into gauge theory and quantum field theory. For example, it led to the discovery of the AdS/CFT correspondence, a theoretical tool that physicists use to translate difficult problems in gauge theory into more mathematically tractable problems in string theory.[5]
Categorical description
Mathematically, branes can be described using the notion of a category.[6] This is a mathematical structure consisting of objects, and for any pair of objects, a set of morphisms between them. In most examples, the objects are mathematical structures (such as sets, vector spaces, or topological spaces) and the morphisms are functions between these structures.[7] One can likewise consider categories where the objects are D-branes and the morphisms between two branes and are states of open strings stretched between and .[8]

In one version of string theory known as the topological B-model, the D-branes are complex submanifolds of certain six-dimensional shapes called Calabi–Yau manifolds, together with additional data that arise physically from having charges at the endpoints of strings.[9] Intuitively, one can think of a submanifold as a surface embedded inside of a Calabi–Yau manifold, although submanifolds can also exist in dimensions different from two.[10] In mathematical language, the category having these branes as its objects is known as the derived category of coherent sheaves on the Calabi–Yau.[11] In another version of string theory called the topological A-model, the D-branes can again be viewed as submanifolds of a Calabi–Yau manifold. Roughly speaking, they are what mathematicians call special Lagrangian submanifolds.[12] This means, among other things, that they have half the dimension of the space in which they sit, and they are length-, area-, or volume-minimizing.[13] The category having these branes as its objects is called the Fukaya category.[14]
The derived category of coherent sheaves is constructed using tools from complex geometry, a branch of mathematics that describes geometric shapes in algebraic terms and solves geometric problems using algebraic equations.[15] On the other hand, the Fukaya category is constructed using symplectic geometry, a branch of mathematics that arose from studies of classical physics. Symplectic geometry studies spaces equipped with a symplectic form, a mathematical tool that can be used to compute area in two-dimensional examples.[16]
The homological mirror symmetry conjecture of Maxim Kontsevich states that the derived category of coherent sheaves on one Calabi–Yau manifold is equivalent in a certain sense to the Fukaya category of a completely different Calabi–Yau manifold.[17] This equivalence provides an unexpected bridge between two branches of geometry, namely complex and symplectic geometry.[18]
See also
- Black brane
- Brane cosmology
- Dirac membrane
- Lagrangian submanifold
- M2-brane
- M5-brane
- NS5-brane
Citations
- ↑ Moore 2005, p. 214
- ↑ M. J. Duff, T. Inami, C. N. Pope, E. Sezgin, and K. S. Stelle, "Semiclassical quantization of the supermembrane", Nucl. Phys. B297 (1988), 515.
- ↑ Moore 2005, p. 214
- ↑ Moore 2005, p. 215
- ↑ Moore 2005, p. 215
- ↑ Aspinwall et al. 2009
- ↑ A basic reference on category theory is Mac Lane 1998.
- ↑ Zaslow 2008, p. 536
- ↑ Zaslow 2008, p. 536
- ↑ Yau and Nadis 2010, p. 165
- ↑ Aspinwal et al. 2009, p. 575
- ↑ Aspinwal et al. 2009, p. 575
- ↑ Yau and Nadis 2010, p. 175
- ↑ Aspinwal et al. 2009, p. 575
- ↑ Yau and Nadis 2010, pp. 180–1
- ↑ Zaslow 2008, p. 531
- ↑ Aspinwall et al. 2009, p. 616
- ↑ Yau and Nadis 2010, p. 181
General and cited references
- Aspinwall, Paul; Bridgeland, Tom; Craw, Alastair et al., eds (2009). Dirichlet Branes and Mirror Symmetry. Clay Mathematics Monographs. 4. American Mathematical Society. ISBN 978-0-8218-3848-8.
- Mac Lane, Saunders (1998). Categories for the Working Mathematician. ISBN 978-0-387-98403-2.
- Moore, Gregory (2005). "What is ... a Brane?". Notices of the AMS 52: 214. https://www.ams.org/notices/200502/what-is.pdf. Retrieved June 7, 2018.
- Yau, Shing-Tung; Nadis, Steve (2010). The Shape of Inner Space: String Theory and the Geometry of the Universe's Hidden Dimensions. Basic Books. ISBN 978-0-465-02023-2.
- Zaslow, Eric (2008). "Mirror Symmetry". in Gowers, Timothy. The Princeton Companion to Mathematics. ISBN 978-0-691-11880-2.
 |