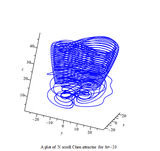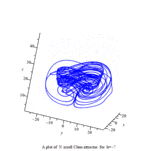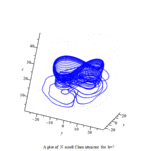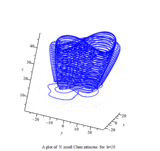
Multiscroll attractor
In the mathematics of dynamical systems, the double-scroll attractor (sometimes known as Chua's attractor) is a strange attractor observed from a physical electronic chaotic circuit (generally, Chua's circuit) with a single nonlinear resistor (see Chua's diode). The double-scroll system is often described by a system of three nonlinear ordinary differential equations and a 3-segment piecewise-linear equation (see Chua's equations). This makes the system easily simulated numerically and easily manifested physically due to Chua's circuits' simple design.
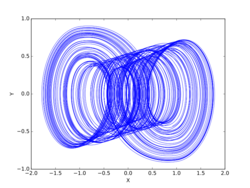
Using a Chua's circuit, this shape is viewed on an oscilloscope using the X, Y, and Z output signals of the circuit. This chaotic attractor is known as the double scroll because of its shape in three-dimensional space, which is similar to two saturn-like rings connected by swirling lines.
The attractor was first observed in simulations, then realized physically after Leon Chua invented the autonomous chaotic circuit which became known as Chua's circuit.[1] The double-scroll attractor from the Chua circuit was rigorously proven to be chaotic[2] through a number of Poincaré return maps of the attractor explicitly derived by way of compositions of the eigenvectors of the 3-dimensional state space.[3]
Numerical analysis of the double-scroll attractor has shown that its geometrical structure is made up of an infinite number of fractal-like layers. Each cross section appears to be a fractal at all scales.[4] Recently, there has also been reported the discovery of hidden attractors within the double scroll.[5]
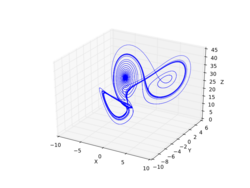
In 1999 Guanrong Chen (陈关荣) and Ueta proposed another double scroll chaotic attractor, called the Chen system or Chen attractor.[6][7]
Chen attractor
The Chen system is defined as follows[7]
[math]\displaystyle{ \frac{dx(t)}{dt}=a(y(t)-x(t)) }[/math]
[math]\displaystyle{ \frac{dy(t)}{dt}=(c-a)x(t)-x(t)z(t)+cy(t) }[/math]
[math]\displaystyle{ \frac{dz(t)}{dt}=x(t)y(t)-bz(t) }[/math]
Plots of Chen attractor can be obtained with the Runge-Kutta method:[8]
parameters: a = 40, c = 28, b = 3
initial conditions: x(0) = -0.1, y(0) = 0.5, z(0) = -0.6
Other attractors
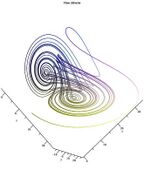
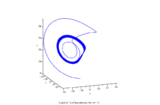
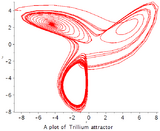
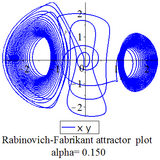
Multiscroll attractors also called n-scroll attractor include the Lu Chen attractor, the modified Chen chaotic attractor, PWL Duffing attractor, Rabinovich Fabrikant attractor, modified Chua chaotic attractor, that is, multiple scrolls in a single attractor.[9]
Lu Chen attractor
An extended Chen system with multiscroll was proposed by Jinhu Lu (吕金虎) and Guanrong Chen[9]
Lu Chen system equation
[math]\displaystyle{ \frac{dx(t)}{dt}=a(y(t)-x(t)) }[/math]
[math]\displaystyle{ \frac{dy(t)}{dt}=x(t)-x(t)z(t)+cy(t)+u }[/math]
[math]\displaystyle{ \frac{dz(t)}{dt}=x(t)y(t)-bz(t) }[/math]
parameters：a = 36, c = 20, b = 3, u = -15.15
initial conditions：x(0) = .1, y(0) = .3, z(0) = -.6
Modified Lu Chen attractor
System equations:[9]
[math]\displaystyle{ \frac{dx(t)}{dt}=a(y(t)-x(t)), }[/math]
[math]\displaystyle{ \frac{dy(t)}{dt}=(c-a)x(t)-x(t)f+cy(t), }[/math]
[math]\displaystyle{ \frac{dz(t)}{dt}=x(t)y(t)-bz(t) }[/math]
In which
[math]\displaystyle{ f = d0z(t) + d1z(t - \tau ) - d2\sin(z(t - \tau )) }[/math]
params := a = 35, c = 28, b = 3, d0 = 1, d1 = 1, d2 = -20..20, tau = .2
initv := x(0) = 1, y(0) = 1, z(0) = 14
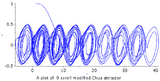
Modified Chua chaotic attractor
In 2001, Tang et al. proposed a modified Chua chaotic system[10]
[math]\displaystyle{ \frac{dx(t)}{dt}= \alpha (y(t)-h) }[/math]
[math]\displaystyle{ \frac{dy(t)}{dt}=x(t)-y(t)+z(t) }[/math]
[math]\displaystyle{ \frac{dz(t)}{dt}=-\beta y(t) }[/math]
In which
[math]\displaystyle{ h := -b \sin\left(\frac{\pi x(t)}{2a}+d\right) }[/math]
params := alpha = 10.82, beta = 14.286, a = 1.3, b = .11, c = 7, d = 0
initv := x(0) = 1, y(0) = 1, z(0) = 0
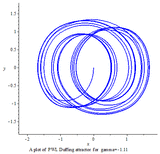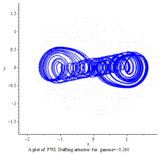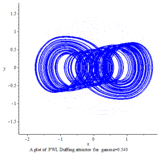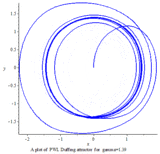
PWL Duffing chaotic attractor
Aziz Alaoui investigated PWL Duffing equation in 2000:[11]
PWL Duffing system:
[math]\displaystyle{ \frac{dx(t)}{dt}=y(t) }[/math]
[math]\displaystyle{ \frac{dy(t)}{dt}=-m_1x(t)-(1/2(m_0-m_1))(|x(t)+1|-|x(t)-1|)-ey(t)+\gamma \cos(\omega t) }[/math]
params := e = .25, gamma = .14+(1/20)i, m0 = -0.845e-1, m1 = .66, omega = 1; c := (.14+(1/20)i)，i=-25...25;
initv := x(0) = 0, y(0) = 0;
Modified Lorenz chaotic system
Miranda & Stone proposed a modified Lorenz system:[12]
[math]\displaystyle{ \frac{dx(t)}{dt} = 1/3*(-(a+1)x(t)+a-c+z(t)y(t))+((1-a)(x(t)^2-y(t)^2)+(2(a+c-z(t)))x(t)y(t)) }[/math][math]\displaystyle{ \frac{1}{3\sqrt{x(t)^2+y(t)^2}} }[/math]
[math]\displaystyle{ \frac{dy(t)}{dt}= 1/3((c-a-z(t))x(t)-(a+1)y(t))+((2(a-1))x(t)y(t)+(a+c-z(t))(x(t)^2-y(t)^2)) }[/math][math]\displaystyle{ \frac{1}{3\sqrt{x(t)^2+y(t)^2}} }[/math]
[math]\displaystyle{ \frac{dz(t)}{dt} = 1/2(3x(t)^2y(t)-y(t)^3)-bz(t) }[/math]
parameters： a = 10, b = 8/3, c = 137/5;
initial conditions： x(0) = -8, y(0) = 4, z(0) = 10
Gallery
Chen attractor
parameters a = 35, c = 27, b = 2.8,x(0) = -.1, y(0) = .3, z(0) = -.6
Lu Chen attractor
Maple plot of N scroll attractor based on Chen with sine and tau
9 scroll modified Chua chaotic attractor
xy plot of 9 scroll modified Chua chaotic attractor
PWL Duffing chaotic attractor xy plot
PWL Duffing chaotic attractor plot
modified Lorenz attractor
Rabinovich Fabrikant attractor xy plot
References
- ↑ Matsumoto, Takashi (December 1984). "A Chaotic Attractor from Chua's Circuit". IEEE Transactions on Circuits and Systems (IEEE) CAS-31 (12): 1055–1058. doi:10.1109/TCS.1984.1085459. http://www.eecs.berkeley.edu/~chua/papers/Matsumoto84.pdf.
- ↑ Chua, Leon; Motomasa Komoru; Takashi Matsumoto (November 1986). "The Double-Scroll Family". IEEE Transactions on Circuits and Systems CAS-33 (11). http://www.eecs.berkeley.edu/~chua/papers/Chua86.pdf.
- ↑ Chua, Leon (2007). "Chua circuits". Scholarpedia 2 (10): 1488. doi:10.4249/scholarpedia.1488. Bibcode: 2007SchpJ...2.1488C.
- ↑ Chua, Leon (2007). "Fractal Geometry of the Double-Scroll Attractor". Scholarpedia 2 (10): 1488. doi:10.4249/scholarpedia.1488. Bibcode: 2007SchpJ...2.1488C.
- ↑ Leonov G.A.; Vagaitsev V.I.; Kuznetsov N.V. (2011). "Localization of hidden Chua's attractors". Physics Letters A 375 (23): 2230–2233. doi:10.1016/j.physleta.2011.04.037. Bibcode: 2011PhLA..375.2230L. http://www.math.spbu.ru/user/nk/PDF/2011-PhysLetA-Hidden-Attractor-Chua.pdf.
- ↑ Chen G., Ueta T. Yet another chaotic attractor. Journal of Bifurcation and Chaos, 1999 9:1465.
- ↑ 7.0 7.1 CHEN, GUANRONG; UETA, TETSUSHI (July 1999). "Yet Another Chaotic Attractor". International Journal of Bifurcation and Chaos 09 (7): 1465–1466. doi:10.1142/s0218127499001024. ISSN 0218-1274. Bibcode: 1999IJBC....9.1465C. http://dx.doi.org/10.1142/s0218127499001024.
- ↑ 阎振亚著 《复杂非线性波的构造性理论及其应用》第17页 SCIENCEP 2007年
- ↑ 9.0 9.1 9.2 Chen, Guanrong; Jinhu Lu (2006). "Generating Multiscroll Chaotic Attractors: Theories, Methods and Applications". International Journal of Bifurcation and Chaos 16 (4): 775–858. doi:10.1142/s0218127406015179. Bibcode: 2006IJBC...16..775L. http://www.ee.cityu.edu.hk/~gchen/pdf/LC-IJBC06-survey.pdf. Retrieved 2012-02-16.
- ↑ Chen, Guanrong; Jinhu Lu (2006). "Generating Multiscroll Chaotic Attractors: Theories, Methods and Applications". International Journal of Bifurcation and Chaos 16 (4): 793–794. doi:10.1142/s0218127406015179. Bibcode: 2006IJBC...16..775L. http://www.ee.cityu.edu.hk/~gchen/pdf/LC-IJBC06-survey.pdf. Retrieved 2012-02-16.
- ↑ J. Lu, G. Chen p. 837
- ↑ J.Liu and G Chen p834
External links
- The double-scroll attractor and Chua's circuit
- Lozi, R.; Pchelintsev, A.N. (2015). "A new reliable numerical method for computing chaotic solutions of dynamical systems: the Chen attractor case". International Journal of Bifurcation and Chaos 25 (13): 1550187–1550412. doi:10.1142/S0218127415501874. Bibcode: 2015IJBC...2550187L. https://hal.archives-ouvertes.fr/hal-01323625/document.
 |  |
