Double pendulum

A double pendulum consists of two pendulums attached end to end.

In physics and mathematics, in the area of dynamical systems, a double pendulum also known as a chaos pendulum is a pendulum with another pendulum attached to its end, forming a simple physical system that exhibits rich dynamic behavior with a strong sensitivity to initial conditions. The motion of a double pendulum is governed by a set of coupled ordinary differential equations and is chaotic.

Analysis and interpretation

Several variants of the double pendulum may be considered; the two limbs may be of equal or unequal lengths and masses, they may be simple pendulums or compound pendulums (also called complex pendulums) and the motion may be in three dimensions or restricted to the vertical plane. In the following analysis, the limbs are taken to be identical compound pendulums of length l and mass m, and the motion is restricted to two dimensions.

Double compound pendulum

Motion of the double compound pendulum (from numerical integration of the equations of motion)

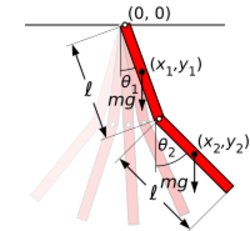
In a compound pendulum, the mass is distributed along its length. If the mass is evenly distributed, then the center of mass of each limb is at its midpoint, and the limb has a moment of inertia of I = 1/12ml² about that point.

It is convenient to use the angles between each limb and the vertical as the generalized coordinates defining the configuration of the system. These angles are denoted θ₁ and θ₂. The position of the center of mass of each rod may be written in terms of these two coordinates. If the origin of the Cartesian coordinate system is taken to be at the point of suspension of the first pendulum, then the center of mass of this pendulum is at:

[math]\displaystyle{ \begin{align} x_1 &= \frac{l}{2} \sin \theta_1 \\ y_1 &= -\frac{l}{2} \cos \theta_1 \end{align} }[/math]

and the center of mass of the second pendulum is at

[math]\displaystyle{ \begin{align} x_2 &= l \left ( \sin \theta_1 + \tfrac{1}{2} \sin \theta_2 \right ) \\ y_2 &= -l \left ( \cos \theta_1 + \tfrac{1}{2} \cos \theta_2 \right ) \end{align} }[/math]

This is enough information to write out the Lagrangian.

Lagrangian

The Lagrangian is

[math]\displaystyle{ \begin{align}L & = \text{kinetic energy} - \text{potential energy} \\ & = \tfrac{1}{2} m \left ( v_1^2 + v_2^2 \right ) + \tfrac{1}{2} I \left ( {\dot \theta_1}^2 + {\dot \theta_2}^2 \right ) - m g \left ( y_1 + y_2 \right ) \\ & = \tfrac{1}{2} m \left ( {\dot x_1}^2 + {\dot y_1}^2 + {\dot x_2}^2 + {\dot y_2}^2 \right ) + \tfrac{1}{2} I \left ( {\dot \theta_1}^2 + {\dot \theta_2}^2 \right ) - m g \left ( y_1 + y_2 \right ) \end{align} }[/math]

The first term is the linear kinetic energy of the center of mass of the bodies and the second term is the rotational kinetic energy around the center of mass of each rod. The last term is the potential energy of the bodies in a uniform gravitational field. The dot-notation indicates the time derivative of the variable in question.

Since (see Chain Rule and List of trigonometric identities)

[math]\displaystyle{ \dot x_1 = \dot \theta_1 \left(\tfrac{l}{2} \cos \theta_1 \right) \quad \rightarrow \quad \dot x_1^2 = \dot \theta_1^2 \left(\tfrac{l^2}{4} \cos^2 \theta_1 \right) }[/math]

[math]\displaystyle{ \dot y_1 = \dot \theta_1 \left(\tfrac{l}{2} \sin \theta_1 \right) \quad \rightarrow \quad \dot y_1^2 = \dot \theta_1^2 \left(\tfrac{l^2}{4} \sin^2 \theta_1 \right) }[/math]

[math]\displaystyle{ \dot x_1^2 + \dot y_1^2 = \dot \theta_1^2 \tfrac{l^2}{4} \left(\cos^2 \theta_1 + \sin^2 \theta_1 \right) = \tfrac{l^2}{4} \dot \theta_1^2 , }[/math]

and

[math]\displaystyle{ \dot x_2 = l \left(\dot \theta_1 \cos \theta_1 + \tfrac{1}{2} \dot \theta_2 \cos \theta_2 \right) \quad \rightarrow \quad \dot x_2^2 = l^2 \left( \dot \theta_1^2 \cos^2 \theta_1 + \dot \theta_1 \dot \theta_2 \cos \theta_1 \cos \theta_2 + \tfrac{1}{4} \dot \theta_2^2 \cos^2 \theta_2 \right) }[/math]

[math]\displaystyle{ \dot y_2 = l \left(\dot \theta_1 \sin \theta_1 + \tfrac{1}{2} \dot \theta_2 \sin \theta_2 \right) \quad \rightarrow \quad \dot y_2^2 = l^2 \left( \dot \theta_1^2 \sin^2 \theta_1 + \dot \theta_1 \dot \theta_2 \sin \theta_1 \sin \theta_2 + \tfrac{1}{4} \dot \theta_2^2 \sin^2 \theta_2 \right) }[/math]

[math]\displaystyle{ \dot x_2^2 + \dot y_2^2 = l^2 \left( \dot \theta_1^2 \cos^2 \theta_1 + \dot \theta_1^2 \sin^2 \theta_1 + \tfrac{1}{4} \dot \theta_2^2 \cos^2 \theta_2 + \tfrac{1}{4} \dot \theta_2^2 \sin^2 \theta_2 + \dot \theta_1 \dot \theta_2 \cos \theta_1 \cos \theta_2 + \dot \theta_1 \dot \theta_2 \sin \theta_1 \sin \theta_2 \right) }[/math]

[math]\displaystyle{ = l^2 \left( \dot \theta_1^2 + \tfrac{1}{4} \dot \theta_2^2 + \dot \theta_1 \dot \theta_2 \cos \left(\theta_1 - \theta_2 \right) \right), }[/math]

substituting the coordinates above and rearranging the equation gives

[math]\displaystyle{ L = \tfrac{m l^2}{2} \left(\tfrac{1}{4} \dot \theta_1^2 + \dot \theta_1^2 + \tfrac{1}{4} \dot \theta_2^2 + \dot \theta_1 \dot \theta_2 \cos \left(\theta_1 - \theta_2 \right) \right) + \tfrac{m l^2}{24} \left( \dot \theta_1^2 + \dot \theta_2^2 \right) - m g \left(y_1 + y_2 \right) }[/math]

[math]\displaystyle{ = \tfrac{1}{6} m l^2 \left ( {\dot \theta_2}^2 + 4 {\dot \theta_1}^2 + 3 {\dot \theta_1} {\dot \theta_2} \cos (\theta_1-\theta_2) \right ) + \tfrac{1}{2} m g l \left ( 3 \cos \theta_1 + \cos \theta_2 \right ). }[/math]

The Euler-Lagrange equations then give the two following second-order, non-linear differential equations in [math]\displaystyle{ (\theta_1,\theta_2) }[/math]:

[math]\displaystyle{ \begin{array}{l} m_2 \left(g \sin \left(\theta _1\right)+l_2 \left(\left(\theta _2'\right){}^2 \sin \left(\theta _1-\theta _2\right)+\theta _2'' \cos \left(\theta _1-\theta _2\right)\right)+l_1 \theta _1''\right)+m_1 \left(g \sin \left(\theta _1\right)+l_1 \theta _1''\right)=0 \\ g \sin \left(\theta _2\right)+l_1 \left(\theta _1'' \cos \left(\theta _1-\theta _2\right)-\left(\theta _1'\right){}^2 \sin \left(\theta _1-\theta _2\right)\right)+l_2 \theta _2''=0 \\ \end{array} }[/math]

No closed form solutions for θ₁ and θ₂ as functions of time are known, therefore solving the system can only be done numerically, using the Runge Kutta method or similar techniques.

Parametric plot for the time evolution of the angles of a double pendulum. It can be noticed that the graph resembles a Brownian motion.

Chaotic motion

Graph of the time for the pendulum to flip over as a function of initial conditions

Long exposure of double pendulum exhibiting chaotic motion (tracked with an LED)

The double pendulum undergoes chaotic motion, and shows a sensitive dependence on initial conditions. The image to the right shows the amount of elapsed time before the pendulum flips over, as a function of initial position when released at rest. Here, the initial value of θ₁ ranges along the x-direction from −3.14 to 3.14. The initial value θ₂ ranges along the y-direction, from −3.14 to 3.14. The colour of each pixel indicates whether either pendulum flips within:

• [math]\displaystyle{ \sqrt{\frac{l}{g}} }[/math] (black)
• [math]\displaystyle{ 10\sqrt{\frac{l}{g}} }[/math] (red)
• [math]\displaystyle{ 100\sqrt{\frac{l}{g}} }[/math] (green)
• [math]\displaystyle{ 1000\sqrt{\frac{l}{g}} }[/math] (blue) or
• [math]\displaystyle{ 10000\sqrt{\frac{l}{g}} }[/math] (purple).

Three double pendulums with near identical initial conditions diverge over time displaying the chaotic nature of the system.

Initial conditions that do not lead to a flip within [math]\displaystyle{ 10000\sqrt{\frac{l}{g}} }[/math] are plotted white.

The boundary of the central white region is defined in part by energy conservation with the following curve:

[math]\displaystyle{ 3 \cos \theta_1 + \cos \theta_2 = 2. }[/math]

Within the region defined by this curve, that is if

[math]\displaystyle{ 3 \cos \theta_1 + \cos \theta_2 \gt 2, }[/math]

then it is energetically impossible for either pendulum to flip. Outside this region, the pendulum can flip, but it is a complex question to determine when it will flip. Similar behavior is observed for a double pendulum composed of two point masses rather than two rods with distributed mass.

The lack of a natural excitation frequency has led to the use of double pendulum systems in seismic resistance designs in buildings, where the building itself is the primary inverted pendulum, and a secondary mass is connected to complete the double pendulum.

See also

• Double inverted pendulum
• Pendulum (mechanics)
• Trebuchet
• Bolas
• Mass damper
• Mid-20th century physics textbooks use the term "double pendulum" to mean a single bob suspended from a string which is in turn suspended from a V-shaped string. This type of pendulum, which produces Lissajous curves, is now referred to as a Blackburn pendulum.

References

• Meirovitch, Leonard (1986). Elements of Vibration Analysis (2nd ed.). McGraw-Hill Science/Engineering/Math. ISBN 0-07-041342-8. 
• Eric W. Weisstein, Double pendulum (2005), ScienceWorld (contains details of the complicated equations involved) and "Double Pendulum" by Rob Morris, Wolfram Demonstrations Project, 2007 (animations of those equations).
• Peter Lynch, Double Pendulum, (2001). (Java applet simulation.)
• Northwestern University, Double Pendulum , (Java applet simulation.)
• Theoretical High-Energy Astrophysics Group at UBC, Double pendulum, (2005).

External links

• Animations and explanations of a double pendulum and a physical double pendulum (two square plates) by Mike Wheatland (Univ. Sydney)

• Interactive Open Source Physics JavaScript simulation with detailed equations double pendulum
• Interactive Javascript simulation of a double pendulum
• Double pendulum physics simulation from www.myphysicslab.com using open source JavaScript code
• Simulation, equations and explanation of Rott's pendulum
• Double Pendulum Simulator - An open source simulator written in C++ using the Qt toolkit.
• Online Java simulator of the Imaginary exhibition.