Percolation threshold

From HandWiki
Short description: Threshold of percolation theory models
Network science
Internet_map_1024.jpg
Network types
Graphs
Features
Types
Models
Topology
Dynamics
  • Lists
  • Categories

The percolation threshold is a mathematical concept in percolation theory that describes the formation of long-range connectivity in random systems. Below the threshold a giant connected component does not exist; while above it, there exists a giant component of the order of system size. In engineering and coffee making, percolation represents the flow of fluids through porous media, but in the mathematics and physics worlds it generally refers to simplified lattice models of random systems or networks (graphs), and the nature of the connectivity in them. The percolation threshold is the critical value of the occupation probability p, or more generally a critical surface for a group of parameters p1, p2, ..., such that infinite connectivity (percolation) first occurs.[1]

Percolation models

The most common percolation model is to take a regular lattice, like a square lattice, and make it into a random network by randomly "occupying" sites (vertices) or bonds (edges) with a statistically independent probability p. At a critical threshold pc, large clusters and long-range connectivity first appear, and this is called the percolation threshold. Depending on the method for obtaining the random network, one distinguishes between the site percolation threshold and the bond percolation threshold. More general systems have several probabilities p1, p2, etc., and the transition is characterized by a critical surface or manifold. One can also consider continuum systems, such as overlapping disks and spheres placed randomly, or the negative space (Swiss-cheese models).

To understand the threshold, you can consider a quantity such as the probability that there is a continuous path from one boundary to another along occupied sites or bonds—that is, within a single cluster. For example, one can consider a square system, and ask for the probability P that there is path from the top boundary to the bottom boundary. As a function of the occupation probability p, one finds a sigmoidal plot that goes from P=0 at p=0 to P=1 at p=1. The larger the square is compared to the lattice spacing, the sharper the transition will be. When the system size goes to infinity, P(p) will be a step function at the threshold value pc. For finite large systems, P(pc) is a constant whose value depends upon the shape of the system; for the square system discussed above, P(pc)=​1⁄2 exactly for any lattice by a simple symmetry argument.

There are other signatures of the critical threshold. For example, the size distribution (number of clusters of size s) drops off as a power-law for large s at the threshold, ns(pc) ~ s−τ, where τ is a dimension-dependent percolation critical exponents. For an infinite system, the critical threshold corresponds to the first point (as p increases) where the size of the clusters become infinite.

In the systems described so far, it has been assumed that the occupation of a site or bond is completely random—this is the so-called Bernoulli percolation. For a continuum system, random occupancy corresponds to the points being placed by a Poisson process. Further variations involve correlated percolation, such as percolation clusters related to Ising and Potts models of ferromagnets, in which the bonds are put down by the Fortuin–Kasteleyn method.[2] In bootstrap or k-sat percolation, sites and/or bonds are first occupied and then successively culled from a system if a site does not have at least k neighbors. Another important model of percolation, in a different universality class altogether, is directed percolation, where connectivity along a bond depends upon the direction of the flow.

Over the last several decades, a tremendous amount of work has gone into finding exact and approximate values of the percolation thresholds for a variety of these systems. Exact thresholds are only known for certain two-dimensional lattices that can be broken up into a self-dual array, such that under a triangle-triangle transformation, the system remains the same. Studies using numerical methods have led to numerous improvements in algorithms and several theoretical discoveries.

Simple duality in two dimensions implies that all fully triangulated lattices (e.g., the triangular, union jack, cross dual, martini dual and asanoha or 3-12 dual, and the Delaunay triangulation) all have site thresholds of ​1⁄2, and self-dual lattices (square, martini-B) have bond thresholds of ​1⁄2.

The notation such as (4,82) comes from Grünbaum and Shephard,[3] and indicates that around a given vertex, going in the clockwise direction, one encounters first a square and then two octagons. Besides the eleven Archimedean lattices composed of regular polygons with every site equivalent, many other more complicated lattices with sites of different classes have been studied.

Error bars in the last digit or digits are shown by numbers in parentheses. Thus, 0.729724(3) signifies 0.729724 ± 0.000003, and 0.74042195(80) signifies 0.74042195 ± 0.00000080. The error bars variously represent one or two standard deviations in net error (including statistical and expected systematic error), or an empirical confidence interval, depending upon the source.

Percolation on networks

For a random tree-like network (i.e., a connected network with no cycle) without degree-degree correlation, it can be shown that such network can have a giant component, and the percolation threshold (transmission probability) is given by

[math]\displaystyle{ p_c = \frac{1}{g_1'(1)} = \frac{\langle k \rangle}{\langle k^2 \rangle - \langle k \rangle} }[/math].

Where [math]\displaystyle{ g_1(z) }[/math] is the generating function corresponding to the excess degree distribution, [math]\displaystyle{ {\langle k \rangle} }[/math] is the average degree of the network and [math]\displaystyle{ {\langle k^2 \rangle} }[/math] is the second moment of the degree distribution. So, for example, for an ER network, since the degree distribution is a Poisson distribution, the threshold is at [math]\displaystyle{ p_c = {\langle k \rangle}^{-1} }[/math].

In networks with low clustering, [math]\displaystyle{ 0 \lt C \ll 1 }[/math], the critical point gets scaled by [math]\displaystyle{ (1-C)^{-1} }[/math] such that: [4]

[math]\displaystyle{ p_c = \frac{1}{1-C}\frac{1}{g_1'(1)}. }[/math]

This indicates that for a given degree distribution, the clustering leads to a larger percolation threshold, mainly because for a fixed number of links, the clustering structure reinforces the core of the network with the price of diluting the global connections. For networks with high clustering, strong clustering could induce the core–periphery structure, in which the core and periphery might percolate at different critical points, and the above approximate treatment is not applicable.[5]

Percolation in 2D

Thresholds on Archimedean lattices

This is a picture[6] of the 11 Archimedean Lattices or Uniform tilings, in which all polygons are regular and each vertex is surrounded by the same sequence of polygons. The notation "(34, 6)", for example, means that every vertex is surrounded by four triangles and one hexagon. Some common names that have been given to these lattices are listed in the table below.
Lattice z [math]\displaystyle{ \overline z }[/math] Site percolation threshold Bond percolation threshold
3-12 or super-kagome, (3, 122 ) 3 3 0.807900764... = (1 − 2 sin (π/18))​1⁄2[7] 0.74042195(80),[8] 0.74042077(2),[9] 0.740420800(2),[10] 0.7404207988509(8),[11][12] 0.740420798850811610(2),[13]
cross, truncated trihexagonal (4, 6, 12) 3 3 0.746,[14] 0.750,[15] 0.747806(4),[7] 0.7478008(2)[11] 0.6937314(1),[11] 0.69373383(72),[8] 0.693733124922(2)[13]
square octagon, bathroom tile, 4-8, truncated square

(4, 82)

3 - 0.729,[14] 0.729724(3),[7] 0.7297232(5)[11] 0.6768,[16] 0.67680232(63),[8] 0.6768031269(6),[11] 0.6768031243900113(3),[13]
honeycomb (63) 3 3 0.6962(6),[17] 0.697040230(5),[11] 0.6970402(1),[18] 0.6970413(10),[19] 0.697043(3),[7] 0.652703645... = 1-2 sin (π/18), 1+ p3-3p2=0[20]
kagome (3, 6, 3, 6) 4 4 0.652703645... = 1 − 2 sin(π/18)[20] 0.5244053(3),[21] 0.52440516(10),[19] 0.52440499(2),[18] 0.524404978(5),[9] 0.52440572...,[22] 0.52440500(1),[10] 0.524404999173(3),[11][12] 0.524404999167439(4)[23] 0.52440499916744820(1)[13]
ruby,[24] rhombitrihexagonal (3, 4, 6, 4) 4 4 0.620,[14] 0.621819(3),[7] 0.62181207(7)[11] 0.52483258(53),[8] 0.5248311(1),[11] 0.524831461573(1)[13]
square (44) 4 4 0.59274(10),[25] 0.59274605079210(2),[23] 0.59274601(2),[11] 0.59274605095(15),[26] 0.59274621(13),[27] 0.592746050786(3),[28] 0.59274621(33),[29] 0.59274598(4),[30][31] 0.59274605(3),[18] 0.593(1),[32] 0.591(1),[33] 0.569(13),[34] 0.59274(5)[35] ​1⁄2
snub hexagonal, maple leaf[36] (34,6) 5 5 0.579[15] 0.579498(3)[7] 0.43430621(50),[8] 0.43432764(3),[11] 0.4343283172240(6),[13]
snub square, puzzle (32, 4, 3, 4 ) 5 5 0.550,[14][37] 0.550806(3)[7] 0.41413743(46),[8] 0.4141378476(7),[11] 0.4141378565917(1),[13]
frieze, elongated triangular(33, 42) 5 5 0.549,[14] 0.550213(3),[7] 0.5502(8)[38] 0.4196(6),[38] 0.41964191(43),[8] 0.41964044(1),[11] 0.41964035886369(2) [13]
triangular (36) 6 6 ​1⁄2 0.347296355... = 2 sin (π/18), 1 + p3 − 3p = 0[20]

Note: sometimes "hexagonal" is used in place of honeycomb, although in some fields, a triangular lattice is also called a hexagonal lattice. z = bulk coordination number.

2D lattices with extended and complex neighborhoods

In this section, sq-1,2,3 corresponds to square (NN+2NN+3NN),[39] etc. Equivalent to square-2N+3N+4N,[40] sq(1,2,3).[41] tri = triangular, hc = honeycomb.

Lattice z Site percolation threshold Bond percolation threshold
sq-1, sq-2, sq-3, sq-5 4 0.5927...[39][40] (square site)
sq-1,2, sq-2,3, sq-3,5 8 0.407...[39][40][42] (square matching) 0.25036834(6),[18] 0.2503685,[43] 0.25036840(4)[44]
sq-1,3 8 0.337[39][40] 0.2214995[43]
sq-2,5: 2NN+5NN 8 0.337[40]
hc-1,2,3: honeycomb-NN+2NN+3NN 12 0.300,[41] 0.300,[15] 0.302960... = 1-pc(site, hc) [45]
tri-1,2: triangular-NN+2NN 12 0.295,[41] 0.289,[15] 0.290258(19)[46]
tri-2,3: triangular-2NN+3NN 12 0.232020(36),[47] 0.232020(20)[46]
sq-4: square-4NN 8 0.270...[40]
sq-1,5: square-NN+5NN (r ≤ 2) 8 0.277[40]
sq-1,2,3: square-NN+2NN+3NN 12 0.292,[48] 0.290(5) [49] 0.289,[15] 0.288,[39][40] 0.1522203[43]
sq-2,3,5: square-2NN+3NN+5NN 12 0.288[40]
sq-1,4: square-NN+4NN 12 0.236[40]
sq-2,4: square-2NN+4NN 12 0.225[40]
tri-4: triangular-4NN 12 0.192450(36),[47] 0.1924428(50)[46]
hc-2,4: honeycomb-2NN+4NN 12 0.2374[50]
tri-1,3: triangular-NN+3NN 12 0.264539(21)[46]
tri-1,2,3: triangular-NN+2NN+3NN 18 0.225,[48] 0.215,[15] 0.215459(36)[47] 0.2154657(17)[46]
sq-3,4: 3NN+4NN 12 0.221[40]
sq-1,2,5: NN+2NN+5NN 12 0.240[40] 0.13805374[43]
sq-1,3,5: NN+3NN+5NN 12 0.233[40]
sq-4,5: 4NN+5NN 12 0.199[40]
sq-1,2,4: NN+2NN+4NN 16 0.219[40]
sq-1,3,4: NN+3NN+4NN 16 0.208[40]
sq-2,3,4: 2NN+3NN+4NN 16 0.202[40]
sq-1,4,5: NN+4NN+5NN 16 0.187[40]
sq-2,4,5: 2NN+4NN+5NN 16 0.182[40]
sq-3,4,5: 3NN+4NN+5NN 16 0.179[40]
sq-1,2,3,5: NN+2NN+3NN+5NN 16 0.208[40] 0.1032177[43]
tri-4,5: 4NN+5NN 18 0.140250(36),[47]
sq-1,2,3,4: NN+2NN+3NN+4NN ([math]\displaystyle{ r \le \sqrt{5} }[/math]) 20 0.19671(9),[51] 0.196,[40] 0.196724(10)[52] 0.0841509[43]
sq-1,2,4,5: NN+2NN+4NN+5NN 20 0.177[40]
sq-1,3,4,5: NN+3NN+4NN+5NN 20 0.172[40]
sq-2,3,4,5: 2NN+3NN+4NN+5NN 20 0.167[40]
sq-1,2,3,5,6: NN+2NN+3NN+5NN+6NN 20 0.0783110[43]
sq-1,2,3,4,5: NN+2NN+3NN+4NN+5NN ([math]\displaystyle{ r \le \sqrt{8} }[/math]) 24 0.164[40]
tri-1,4,5: NN+4NN+5NN 24 0.131660(36)[47]
sq-1,...,6: NN+...+6NN (r≤3) 28 0.142[15] 0.0558493[43]
tri-2,3,4,5: 2NN+3NN+4NN+5NN 30 0.117460(36)[47] 0.135823(27)[46]
tri-1,2,3,4,5: NN+2NN+3NN+4NN+5NN
36 0.115,[15] 0.115740(36),[47] 0.1157399(58) [46]
sq-1,...,7: NN+...+7NN ([math]\displaystyle{ r \le \sqrt{10} }[/math]) 36 0.113[15] 0.04169608[43]
square: square distance ≤ 4 40 0.105(5)[49]
sq-(1,...,8: NN+..+8NN ([math]\displaystyle{ r \le \sqrt{13} }[/math]) 44 0.095,[37] 0.095765(5),[52] 0.09580(2)[51]
sq-1,...,9: NN+..+9NN (r≤4) 48 0.086[15] 0.02974268[43]
sq-1,...,11: NN+...+11NN ([math]\displaystyle{ r \le \sqrt{18} }[/math]) 60 0.02301190(3)[43]
sq-1,...,23 (r ≤ 7) 148 0.008342595[44]
sq-1,...,32: NN+...+32NN ([math]\displaystyle{ r \le \sqrt{72} }[/math]) 224 0.0053050415(33)[43]
sq-1,...,86: NN+...+86NN (r≤15) 708 0.001557644(4)[53]
sq-1,...,141: NN+...+141NN ([math]\displaystyle{ r \le \sqrt{389} }[/math]) 1224 0.000880188(90)[43]
sq-1,...,185: NN+...+185NN (r≤23) 1652 0.000645458(4)[53]
sq-1,...,317: NN+...+317NN (r≤31) 3000 0.000349601(3)[53]
sq-1,...,413: NN+...+413NN ([math]\displaystyle{ r \le \sqrt{1280} }[/math]) 4016 0.0002594722(11)[43]
square: square distance ≤ 6 84 0.049(5)[49]
square: square distance ≤ 8 144 0.028(5)[49]
square: square distance ≤ 10 220 0.019(5)[49]
2x2 lattice squares* (also above) 20 φc = 0.58365(2),[52] pc = 0.196724(10),[52] 0.19671(9),[51]
3x3 lattice squares* (also above) 44 φc = 0.59586(2),[52] pc = 0.095765(5),[52] 0.09580(2) [51]
4x4 lattice squares* 76 φc = 0.60648(1),[52] pc = 0.0566227(15),[52] 0.05665(3),[51]
5x5 lattice squares* 116 φc = 0.61467(2),[52] pc = 0.037428(2),[52] 0.03745(2),[51]
6x6 lattice squares* 220 pc = 0.02663(1),[51]
10x10 lattice squares* 436 φc = 0.36391(2),[52] pc = 0.0100576(5) [52]

Here NN = nearest neighbor, 2NN = second nearest neighbor (or next nearest neighbor), 3NN = third nearest neighbor (or next-next nearest neighbor), etc. These are also called 2N, 3N, 4N respectively in some papers.[39]

  • For overlapping or touching squares, [math]\displaystyle{ p_c }[/math](site) given here is the net fraction of sites occupied [math]\displaystyle{ \phi_c }[/math] similar to the [math]\displaystyle{ \phi_c }[/math] in continuum percolation. The case of a 2×2 square is equivalent to percolation of a square lattice NN+2NN+3NN+4NN or sq-1,2,3,4 with threshold [math]\displaystyle{ 1-(1-\phi_c)^{1/4} = 0.196724(10)\ldots }[/math] with [math]\displaystyle{ \phi_c= 0.58365(2) }[/math].[52] The 3×3 square corresponds to sq-1,2,3,4,5,6,7,8 with z=44 and [math]\displaystyle{ p_c=1-(1-\phi_c)^{1/9} = 0.095765(5)\ldots }[/math]. The value of z for a k x k square is (2k+1)2-5. For larger overlapping squares, see.[52]

2D distorted lattices

Here, one distorts a regular lattice of unit spacing by moving vertices uniformly within the box [math]\displaystyle{ (x-\alpha,x+\alpha),(y-\alpha,y+\alpha) }[/math], and considers percolation when sites are within Euclidean distance [math]\displaystyle{ d }[/math] of each other.


Lattice [math]\displaystyle{ \overline z }[/math] [math]\displaystyle{ \alpha }[/math] [math]\displaystyle{ d }[/math] Site percolation threshold Bond percolation threshold
square 0.2 1.1 0.8025(2)[54]
0.2 1.2 0.6667(5)[54]
0.1 1.1 0.6619(1)[54]


Overlapping shapes on 2D lattices

Site threshold is number of overlapping objects per lattice site. k is the length (net area). Overlapping squares are shown in the complex neighborhood section. Here z is the coordination number to k-mers of either orientation, with [math]\displaystyle{ z = k^2+10k-2 }[/math] for [math]\displaystyle{ 1 \times k }[/math] sticks.

System k z Site coverage φc Site percolation threshold pc
1 x 2 dimer, square lattice 2 22 0.54691[51]

0.5483(2)[55]

0.17956(3)[51]

0.18019(9)[55]

1 x 2 aligned dimer, square lattice 2 14 0.5715(18)[55] 0.3454(13) [55]
1 x 3 trimer, square lattice 3 37 0.49898[51]

0.50004(64)[55]

0.10880(2)[51]

0.1093(2)[55]

1 x 4 stick, square lattice 4 54 0.45761[51] 0.07362(2)[51]
1 x 5 stick, square lattice 5 73 0.42241[51] 0.05341(1)[51]
1 x 6 stick, square lattice 6 94 0.39219[51] 0.04063(2)[51]

The coverage is calculated from [math]\displaystyle{ p_c }[/math] by [math]\displaystyle{ \phi_c = 1-(1-p_c)^{2 k} }[/math] for [math]\displaystyle{ 1 \times k }[/math] sticks, because there are [math]\displaystyle{ 2k }[/math] sites where a stick will cause an overlap with a given site.

For aligned [math]\displaystyle{ 1 \times k }[/math] sticks: [math]\displaystyle{ \phi_c = 1-(1-p_c)^{k} }[/math]

Approximate formulas for thresholds of Archimedean lattices

Lattice z Site percolation threshold Bond percolation threshold
(3, 122 ) 3
(4, 6, 12) 3
(4, 82) 3 0.676835..., 4p3 + 3p4 − 6 p5 − 2 p6 = 1[56]
honeycomb (63) 3
kagome (3, 6, 3, 6) 4 0.524430..., 3p2 + 6p3 − 12 p4+ 6 p5 − p6 = 1[57]
(3, 4, 6, 4) 4
square (44) 4 ​1⁄2 (exact)
(34,6 ) 5 0.434371..., 12p3 + 36p4 − 21p5 − 327 p6 + 69p7 + 2532p8 − 6533 p9 + 8256 p10 − 6255p11 + 2951p12 − 837 p13 + 126 p14 − 7p15 = 1[citation needed]
snub square, puzzle (32, 4, 3, 4 ) 5
(33, 42) 5
triangular (36) 6 ​1⁄2 (exact)


AB percolation and colored percolation in 2D

In AB percolation, a [math]\displaystyle{ p_\mathrm{site} }[/math] is the proportion of A sites among B sites, and bonds are drawn between sites of opposite species.[58] It is also called antipercolation.

In colored percolation, occupied sites are assigned one of [math]\displaystyle{ n }[/math] colors with equal probability, and connection is made along bonds between neighbors of different colors.[59]

Lattice z [math]\displaystyle{ \overline z }[/math] Site percolation threshold
triangular AB 6 6 0.2145,[58] 0.21524(34),[60] 0.21564(3)[61]
AB on square-covering lattice 6 6 [math]\displaystyle{ 1-\sqrt{1-p_c(site,sq)} = 0.361835 }[/math][62]
square three-color 4 4 0.80745(5)[59]
square four-color 4 4 0.73415(4)[59]
square five-color 4 4 0.69864(7)[59]
square six-color 4 4 0.67751(5)[59]
triangular two-color 6 6 0.72890(4)[59]
triangular three-color 6 6 0.63005(4)[59]
triangular four-color 6 6 0.59092(3)[59]
triangular five-color 6 6 0.56991(5)[59]
triangular six-color 6 6 0.55679(5)[59]

Site-bond percolation in 2D

Site bond percolation. Here [math]\displaystyle{ p_s }[/math] is the site occupation probability and [math]\displaystyle{ p_b }[/math] is the bond occupation probability, and connectivity is made only if both the sites and bonds along a path are occupied. The criticality condition becomes a curve [math]\displaystyle{ f(p_{s},p_{b}) }[/math] = 0, and some specific critical pairs [math]\displaystyle{ (p_{s},p_{b}) }[/math] are listed below.

Square lattice:

Lattice z [math]\displaystyle{ \overline z }[/math] Site percolation threshold Bond percolation threshold
square 4 4 0.615185(15)[63] 0.95
0.667280(15)[63] 0.85
0.732100(15)[63] 0.75
0.75 0.726195(15)[63]
0.815560(15)[63] 0.65
0.85 0.615810(30)[63]
0.95 0.533620(15)[63]

Honeycomb (hexagonal) lattice:

Lattice z [math]\displaystyle{ \overline z }[/math] Site percolation threshold Bond percolation threshold
honeycomb 3 3 0.7275(5)[64] 0.95
0. 0.7610(5)[64] 0.90
0.7986(5)[64] 0.85
0.80 0.8481(5)[64]
0.8401(5)[64] 0.80
0.85 0.7890(5)[64]
0.90 0.7377(5)[64]
0.95 0.6926(5)[64]

Kagome lattice:

Lattice z [math]\displaystyle{ \overline z }[/math] Site percolation threshold Bond percolation threshold
kagome 4 4 0.6711(4),[64] 0.67097(3)[65] 0.95
0.6914(5),[64] 0.69210(2)[65] 0.90
0.7162(5),[64] 0.71626(3)[65] 0.85
0.7428(5),[64] 0.74339(3)[65] 0.80
0.75 0.7894(9)[64]
0.7757(8),[64] 0.77556(3)[65] 0.75
0.80 0.7152(7)[64]
0.81206(3)[65] 0.70
0.85 0.6556(6)[64]
0.85519(3)[65] 0.65
0.90 0.6046(5)[64]
0.90546(3)[65] 0.60
0.95 0.5615(4)[64]
0.96604(4)[65] 0.55
0.9854(3)[65] 0.53

* For values on different lattices, see "An investigation of site-bond percolation on many lattices".[64]

Approximate formula for site-bond percolation on a honeycomb lattice

Lattice z [math]\displaystyle{ \overline z }[/math] Threshold Notes
(63) honeycomb 3 3 [math]\displaystyle{ p_b p_s [1 - (\sqrt{p_{bc}}/(3-p_{bc}))(\sqrt{p_b} - \sqrt{p_{bc}})] = p_{bc} }[/math], When equal: ps = pb = 0.82199 approximate formula, ps = site prob., pb = bond prob., pbc = 1 − 2 sin (π/18),[19] exact at ps=1, pb=pbc.

Archimedean duals (Laves lattices)

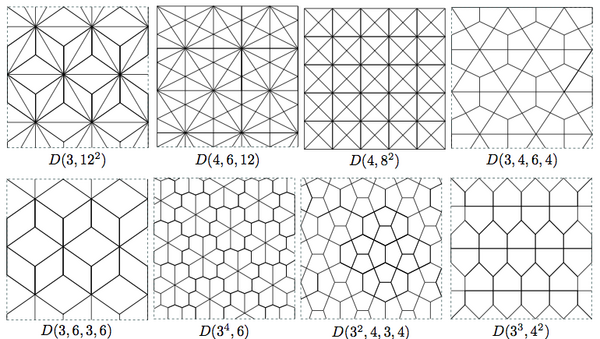
Example image caption

Laves lattices are the duals to the Archimedean lattices. Drawings from.[6] See also Uniform tilings.

Lattice z [math]\displaystyle{ \overline z }[/math] Site percolation threshold Bond percolation threshold
Cairo pentagonal

D(32,4,3,4)=(​2⁄3)(53)+(​1⁄3)(54)

3,4 3 ​1⁄3 0.6501834(2),[11] 0.650184(5)[6] 0.585863... = 1 − pcbond(32,4,3,4)
Pentagonal D(33,42)=(​1⁄3)(54)+(​2⁄3)(53) 3,4 3 ​1⁄3 0.6470471(2),[11] 0.647084(5),[6] 0.6471(6)[38] 0.580358... = 1 − pcbond(33,42), 0.5800(6)[38]
D(34,6)=(​1⁄5)(46)+(​4⁄5)(43) 3,6 3 ​3⁄5 0.639447[6] 0.565694... = 1 − pcbond(34,6 )
dice, rhombille tiling

D(3,6,3,6) = (​1⁄3)(46) + (​2⁄3)(43)

3,6 4 0.5851(4),[66] 0.585040(5)[6] 0.475595... = 1 − pcbond(3,6,3,6 )
ruby dual

D(3,4,6,4) = (​1⁄6)(46) + (​2⁄6)(43) + (​3⁄6)(44)

3,4,6 4 0.582410(5)[6] 0.475167... = 1 − pcbond(3,4,6,4 )
union jack, tetrakis square tiling

D(4,82) = (​1⁄2)(34) + (​1⁄2)(38)

4,8 6 ​1⁄2 0.323197... = 1 − pcbond(4,82 )
bisected hexagon,[67] cross dual

D(4,6,12)= (​1⁄6)(312)+(​2⁄6)(36)+(​1⁄2)(34)

4,6,12 6 ​1⁄2 0.306266... = 1 − pcbond(4,6,12)
asanoha (hemp leaf)[68]

D(3, 122)=(​2⁄3)(33)+(​1⁄3)(312)

3,12 6 ​1⁄2 0.259579... = 1 − pcbond(3, 122)

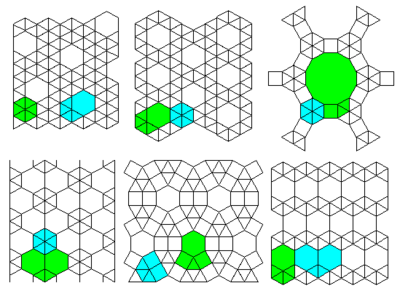
2-uniform lattices

Top 3 lattices: #13 #12 #36
Bottom 3 lattices: #34 #37 #11

20 2 uniform lattices

[3]

Top 2 lattices: #35 #30
Bottom 2 lattices: #41 #42

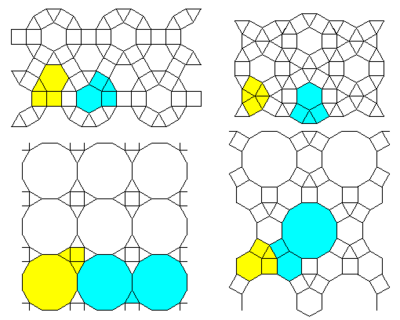
20 2 uniform lattices

[3]

Top 4 lattices: #22 #23 #21 #20
Bottom 3 lattices: #16 #17 #15

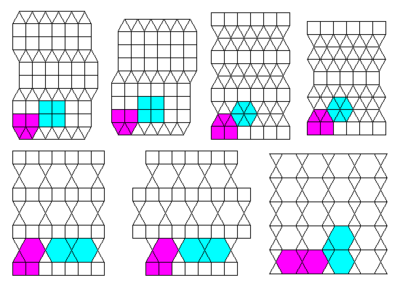
20 2 uniform lattices

[3]

Top 2 lattices: #31 #32
Bottom lattice: #33

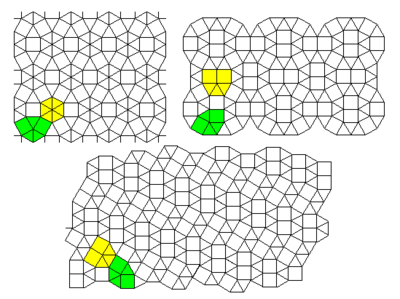
20 2 uniform lattices

[3]

# Lattice z [math]\displaystyle{ \overline z }[/math] Site percolation threshold Bond percolation threshold
41 (​1⁄2)(3,4,3,12) + (​1⁄2)(3, 122) 4,3 3.5 0.7680(2)[69]
42 (​1⁄3)(3,4,6,4) + (​2⁄3)(4,6,12) 4,3 3​1⁄3 0.7157(2)[69]
36 (​1⁄7)(36) + (​6⁄7)(32,4,12) 6,4 4 ​2⁄7 0.6808(2)[69]
15 (​2⁄3)(32,62) + (​1⁄3)(3,6,3,6) 4,4 4 0.6499(2)[69]
34 (​1⁄7)(36) + (​6⁄7)(32,62) 6,4 4 ​2⁄7 0.6329(2)[69]
16 (​4⁄5)(3,42,6) + (​1⁄5)(3,6,3,6) 4,4 4 0.6286(2)[69]
17 (​4⁄5)(3,42,6) + (​1⁄5)(3,6,3,6)* 4,4 4 0.6279(2)[69]
35 (​2⁄3)(3,42,6) + (​1⁄3)(3,4,6,4) 4,4 4 0.6221(2)[69]
11 (​1⁄2)(34,6) + (​1⁄2)(32,62) 5,4 4.5 0.6171(2)[69]
37 (​1⁄2)(33,42) + (​1⁄2)(3,4,6,4) 5,4 4.5 0.5885(2)[69]
30 (​1⁄2)(32,4,3,4) + (​1⁄2)(3,4,6,4) 5,4 4.5 0.5883(2)[69]
23 (​1⁄2)(33,42) + (​1⁄2)(44) 5,4 4.5 0.5720(2)[69]
22 (​2⁄3)(33,42) + (​1⁄3)(44) 5,4 4 ​2⁄3 0.5648(2)[69]
12 (​1⁄4)(36) + (​3⁄4)(34,6) 6,5 5 ​1⁄4 0.5607(2)[69]
33 (​1⁄2)(33,42) + (​1⁄2)(32,4,3,4) 5,5 5 0.5505(2)[69]
32 (​1⁄3)(33,42) + (​2⁄3)(32,4,3,4) 5,5 5 0.5504(2)[69]
31 (​1⁄7)(36) + (​6⁄7)(32,4,3,4) 6,5 5 ​1⁄7 0.5440(2)[69]
13 (​1⁄2)(36) + (​1⁄2)(34,6) 6,5 5.5 0.5407(2)[69]
21 (​1⁄3)(36) + (​2⁄3)(33,42) 6,5 5 ​1⁄3 0.5342(2)[69]
20 (​1⁄2)(36) + (​1⁄2)(33,42) 6,5 5.5 0.5258(2)[69]

Inhomogeneous 2-uniform lattice

2-uniform lattice #37

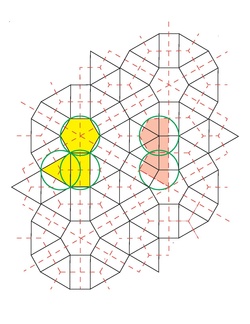
This figure shows something similar to the 2-uniform lattice #37, except the polygons are not all regular—there is a rectangle in the place of the two squares—and the size of the polygons is changed. This lattice is in the isoradial representation in which each polygon is inscribed in a circle of unit radius. The two squares in the 2-uniform lattice must now be represented as a single rectangle in order to satisfy the isoradial condition. The lattice is shown by black edges, and the dual lattice by red dashed lines. The green circles show the isoradial constraint on both the original and dual lattices. The yellow polygons highlight the three types of polygons on the lattice, and the pink polygons highlight the two types of polygons on the dual lattice. The lattice has vertex types (​1⁄2)(33,42) + (​1⁄2)(3,4,6,4), while the dual lattice has vertex types (​1⁄15)(46)+(​6⁄15)(42,52)+(​2⁄15)(53)+(​6⁄15)(52,4). The critical point is where the longer bonds (on both the lattice and dual lattice) have occupation probability p = 2 sin (π/18) = 0.347296... which is the bond percolation threshold on a triangular lattice, and the shorter bonds have occupation probability 1 − 2 sin(π/18) = 0.652703..., which is the bond percolation on a hexagonal lattice. These results follow from the isoradial condition[70] but also follow from applying the star-triangle transformation to certain stars on the honeycomb lattice. Finally, it can be generalized to having three different probabilities in the three different directions, p1, p2 and p3 for the long bonds, and 1 − p1, 1 − p2, and 1 − p3 for the short bonds, where p1, p2 and p3 satisfy the critical surface for the inhomogeneous triangular lattice.

Thresholds on 2D bow-tie and martini lattices

To the left, center, and right are: the martini lattice, the martini-A lattice, the martini-B lattice. Below: the martini covering/medial lattice, same as the 2×2, 1×1 subnet for kagome-type lattices (removed).

Example image caption

Some other examples of generalized bow-tie lattices (a-d) and the duals of the lattices (e-h):

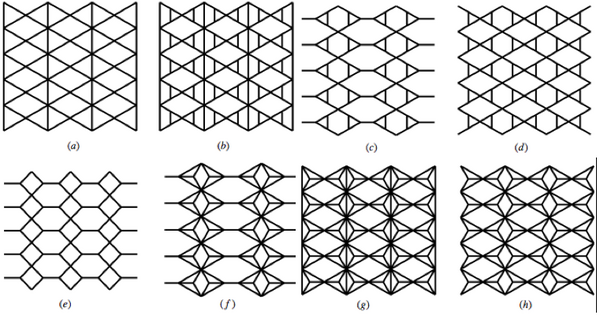
Example image caption
Lattice z [math]\displaystyle{ \overline z }[/math] Site percolation threshold Bond percolation threshold
martini (​3⁄4)(3,92)+(​1⁄4)(93) 3 3 0.764826..., 1 + p4 − 3p3 = 0[71] 0.707107... = 1/√2[72]
bow-tie (c) 3,4 3 ​1⁄7 0.672929..., 1 − 2p3 − 2p4 − 2p5 − 7p6 + 18p7 + 11p8 − 35p9 + 21p10 − 4p11 = 0[73]
bow-tie (d) 3,4 3 ​1⁄3 0.625457..., 1 − 2p2 − 3p3 + 4p4 − p5 = 0[73]
martini-A (​2⁄3)(3,72)+(​1⁄3)(3,73) 3,4 3 ​1⁄3 1/√2[73] 0.625457..., 1 − 2p2 − 3p3 + 4p4 − p5 = 0[73]
bow-tie dual (e) 3,4 3 ​2⁄3 0.595482..., 1-pcbond (bow-tie (a))[73]
bow-tie (b) 3,4,6 3 ​2⁄3 0.533213..., 1 − p − 2p3 -4p4-4p5+156+ 13p7-36p8+19p9+ p10 + p11=0[73]
martini covering/medial (​1⁄2)(33,9) + (​1⁄2)(3,9,3,9) 4 4 0.707107... = 1/√2[72]
martini-B (​1⁄2)(3,5,3,52) + (​1⁄2)(3,52) 3, 5 4 0.618034... = 2/(1 + √5), 1- p2 − p = 0[71][73] ​1⁄2[72][73]
bow-tie dual (f) 3,4,8 4 ​2⁄5 0.466787..., 1 − pcbond (bow-tie (b))[73]
bow-tie (a) (​1⁄2)(32,4,32,4) + (​1⁄2)(3,4,3) 4,6 5 0.5472(2),[38] 0.5479148(7)[74] 0.404518..., 1 − p − 6p2 + 6p3 − p5 = 0[73][75]
bow-tie dual (h) 3,6,8 5 0.374543..., 1 − pcbond(bow-tie (d))[73]
bow-tie dual (g) 3,6,10 5 ​1⁄2 0.547... = pcsite(bow-tie(a)) 0.327071..., 1 − pcbond(bow-tie (c))[73]
martini dual (​1⁄2)(33) + (​1⁄2)(39) 3,9 6 ​1⁄2 0.292893... = 1 − 1/√2[72]

Thresholds on 2D covering, medial, and matching lattices

Lattice z [math]\displaystyle{ \overline z }[/math] Site percolation threshold Bond percolation threshold
(4, 6, 12) covering/medial 4 4 pcbond(4, 6, 12) = 0.693731... 0.5593140(2),[11] 0.559315(1)[citation needed]
(4, 82) covering/medial, square kagome 4 4 pcbond(4,82) = 0.676803... 0.544798017(4),[11] 0.54479793(34)[citation needed]
(34, 6) medial 4 4 0.5247495(5)[11]
(3,4,6,4) medial 4 4 0.51276[11]
(32, 4, 3, 4) medial 4 4 0.512682929(8)[11]
(33, 42) medial 4 4 0.5125245984(9)[11]
square covering (non-planar) 6 6 ​1⁄2 0.3371(1)[56]
square matching lattice (non-planar) 8 8 1 − pcsite(square) = 0.407253... 0.25036834(6)[18]
(4, 6, 12) covering/medial lattice
(4, 82) covering/medial lattice
(3,122) covering/medial lattice (in light grey), equivalent to the kagome (2 × 2) subnet, and in black, the dual of these lattices.
(3,4,6,4) covering/medial lattice, equivalent to the 2-uniform lattice #30, but with facing triangles made into a diamond. This pattern appears in Iranian tilework.[76] such as Western tomb tower, Kharraqan.[77]
(3,4,6,4) medial dual, shown in red, with medial lattice in light gray behind it

Thresholds on 2D chimera non-planar lattices

Lattice z [math]\displaystyle{ \overline z }[/math] Site percolation threshold Bond percolation threshold
K(2,2) 4 4 0.51253(14)[78] 0.44778(15)[78]
K(3,3) 6 6 0.43760(15)[78] 0.35502(15)[78]
K(4,4) 8 8 0.38675(7)[78] 0.29427(12)[78]
K(5,5) 10 10 0.35115(13)[78] 0.25159(13)[78]
K(6,6) 12 12 0.32232(13)[78] 0.21942(11)[78]
K(7,7) 14 14 0.30052(14)[78] 0.19475(9)[78]
K(8,8) 16 16 0.28103(11)[78] 0.17496(10)[78]

Thresholds on subnet lattices

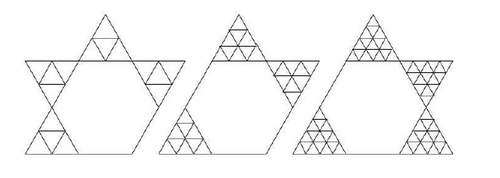
Example image caption

The 2 x 2, 3 x 3, and 4 x 4 subnet kagome lattices. The 2 × 2 subnet is also known as the "triangular kagome" lattice.[79]

Lattice z [math]\displaystyle{ \overline z }[/math] Site percolation threshold Bond percolation threshold
checkerboard – 2 × 2 subnet 4,3 0.596303(1)[80]
checkerboard – 4 × 4 subnet 4,3 0.633685(9)[80]
checkerboard – 8 × 8 subnet 4,3 0.642318(5)[80]
checkerboard – 16 × 16 subnet 4,3 0.64237(1)[80]
checkerboard – 32 × 32 subnet 4,3 0.64219(2)[80]
checkerboard – [math]\displaystyle{ \infty }[/math] subnet 4,3 0.642216(10)[80]
kagome – 2 × 2 subnet = (3, 122) covering/medial 4 pcbond (3, 122) = 0.74042077... 0.600861966960(2),[11] 0.6008624(10),[19] 0.60086193(3)[9]
kagome – 3 × 3 subnet 4 0.6193296(10),[19] 0.61933176(5),[9] 0.61933044(32)[citation needed]
kagome – 4 × 4 subnet 4 0.625365(3),[19] 0.62536424(7)[9]
kagome – [math]\displaystyle{ \infty }[/math] subnet 4 0.628961(2)[19]
kagome – (1 × 1):(2 × 2) subnet = martini covering/medial 4 pcbond(martini) = 1/√2 = 0.707107...
kagome – (1 × 1):(3 × 3) subnet 4,3 0.728355596425196...[9]
kagome – (1 × 1):(4 × 4) subnet 0.738348473943256...[9]
kagome – (1 × 1):(5 × 5) subnet 0.743548682503071...[9]
kagome – (1 × 1):(6 × 6) subnet 0.746418147634282...[9]
kagome – (2 × 2):(3 × 3) subnet
triangular – 2 × 2 subnet 6,4 0.471628788[80]
triangular – 3 × 3 subnet 6,4 0.509077793[80]
triangular – 4 × 4 subnet 6,4 0.524364822[80]
triangular – 5 × 5 subnet 6,4 0.5315976(10)[80]
triangular – [math]\displaystyle{ \infty }[/math] subnet 6,4 0.53993(1)[80]

Thresholds of random sequentially adsorbed objects

(For more results and comparison to the jamming density, see Random sequential adsorption)

system z Site threshold
dimers on a honeycomb lattice 3 0.69,[81] 0.6653 [82]
dimers on a triangular lattice 6 0.4872(8),[81] 0.4873,[82]
aligned linear dimers on a triangular lattice 6 0.5157(2) [83]
aligned linear 4-mers on a triangular lattice 6 0.5220(2)[83]
aligned linear 8-mers on a triangular lattice 6 0.5281(5)[83]
aligned linear 12-mers on a triangular lattice 6 0.5298(8)[83]
linear 16-mers on a triangular lattice 6 aligned 0.5328(7)[83]
linear 32-mers on a triangular lattice 6 aligned 0.5407(6)[83]
linear 64-mers on a triangular lattice 6 aligned 0.5455(4)[83]
aligned linear 80-mers on a triangular lattice 6 0.5500(6)[83]
aligned linear k [math]\displaystyle{ \longrightarrow \infty }[/math] on a triangular lattice 6 0.582(9)[83]
dimers and 5% impurities, triangular lattice 6 0.4832(7)[84]
parallel dimers on a square lattice 4 0.5863[85]
dimers on a square lattice 4 0.5617,[85] 0.5618(1),[86] 0.562,[87] 0.5713[82]
linear 3-mers on a square lattice 4 0.528[87]
3-site 120° angle, 5% impurities, triangular lattice 6 0.4574(9)[84]
3-site triangles, 5% impurities, triangular lattice 6 0.5222(9)[84]
linear trimers and 5% impurities, triangular lattice 6 0.4603(8)[84]
linear 4-mers on a square lattice 4 0.504[87]
linear 5-mers on a square lattice 4 0.490[87]
linear 6-mers on a square lattice 4 0.479[87]
linear 8-mers on a square lattice 4 0.474,[87] 0.4697(1)[86]
linear 10-mers on a square lattice 4 0.469[87]
linear 16-mers on a square lattice 4 0.4639(1)[86]
linear 32-mers on a square lattice 4 0.4747(2)[86]

The threshold gives the fraction of sites occupied by the objects when site percolation first takes place (not at full jamming). For longer k-mers see Ref.[88]

Thresholds of full dimer coverings of two dimensional lattices

Here, we are dealing with networks that are obtained by covering a lattice with dimers, and then consider bond percolation on the remaining bonds. In discrete mathematics, this problem is known as the 'perfect matching' or the 'dimer covering' problem.

system z Bond threshold
Parallel covering, square lattice 6 0.381966...[89]
Shifted covering, square lattice 6 0.347296...[89]
Staggered covering, square lattice 6 0.376825(2)[89]
Random covering, square lattice 6 0.367713(2)[89]
Parallel covering, triangular lattice 10 0.237418...[89]
Staggered covering, triangular lattice 10 0.237497(2)[89]
Random covering, triangular lattice 10 0.235340(1)[89]

Thresholds of polymers (random walks) on a square lattice

System is composed of ordinary (non-avoiding) random walks of length l on the square lattice.[90]

l (polymer length) z Bond percolation
1 4 0.5(exact)[91]
2 4 0.47697(4)[91]
4 4 0.44892(6)[91]
8 4 0.41880(4)[91]

Thresholds of self-avoiding walks of length k added by random sequential adsorption

k z Site thresholds Bond thresholds
1 4 0.593(2)[92] 0.5009(2)[92]
2 4 0.564(2)[92] 0.4859(2)[92]
3 4 0.552(2)[92] 0.4732(2)[92]
4 4 0.542(2)[92] 0.4630(2)[92]
5 4 0.531(2)[92] 0.4565(2)[92]
6 4 0.522(2)[92] 0.4497(2)[92]
7 4 0.511(2)[92] 0.4423(2)[92]
8 4 0.502(2)[92] 0.4348(2)[92]
9 4 0.493(2)[92] 0.4291(2)[92]
10 4 0.488(2)[92] 0.4232(2)[92]
11 4 0.482(2)[92] 0.4159(2)[92]
12 4 0.476(2)[92] 0.4114(2)[92]
13 4 0.471(2)[92] 0.4061(2)[92]
14 4 0.467(2)[92] 0.4011(2)[92]
15 4 0.4011(2)[92] 0.3979(2)[92]

Thresholds on 2D inhomogeneous lattices

Lattice z Site percolation threshold Bond percolation threshold
bow-tie with p = ​1⁄2 on one non-diagonal bond 3 0.3819654(5),[93] [math]\displaystyle{ (3 - \sqrt{5})/2 }[/math][56]

Thresholds for 2D continuum models

System Φc ηc nc
Disks of radius r 0.67634831(2),[94] 0.6763475(6),[95] 0.676339(4),[96] 0.6764(4),[97] 0.6766(5),[98] 0.676(2),[99] 0.679,[100] 0.674[101] 0.676,[102] 0.680[103] 1.1280867(5),[104] 1.1276(9),[105] 1.12808737(6),[94] 1.128085(2),[95] 1.128059(12),[96] 1.13,[citation needed] 0.8[106] 1.43632505(10),[107] 1.43632545(8),[94] 1.436322(2),[95] 1.436289(16),[96] 1.436320(4),[108] 1.436323(3),[109] 1.438(2),[110] 1.216 (48)[111]
Ellipses, ε = 1.5 0.0043[100] 0.00431 2.059081(7)[109]
Ellipses, ε = ​5⁄3 0.65[112] 1.05[112] 2.28[112]
Ellipses, ε = 2 0.6287945(12),[109] 0.63[112] 0.991000(3),[109] 0.99[112] 2.523560(8),[109] 2.5[112]
Ellipses, ε = 3 0.56[112] 0.82[112] 3.157339(8),[109] 3.14[112]
Ellipses, ε = 4 0.5[112] 0.69[112] 3.569706(8),[109] 3.5[112]
Ellipses, ε = 5 0.455,[100] 0.455,[102] 0.46[112] 0.607[100] 3.861262(12),[109] 3.86[100]
Ellipses, ε = 6 4.079365(17)[109]
Ellipses, ε = 7 4.249132(16)[109]
Ellipses, ε = 8 4.385302(15)[109]
Ellipses, ε = 9 4.497000(8)[109]
Ellipses, ε = 10 0.301,[100] 0.303,[102] 0.30[112] 0.358[100] 0.36[112] 4.590416(23)[109] 4.56,[100] 4.5[112]
Ellipses, ε = 15 4.894752(30)[109]
Ellipses, ε = 20 0.178,[100] 0.17[112] 0.196[100] 5.062313(39),[109] 4.99[100]
Ellipses, ε = 50 0.081[100] 0.084[100] 5.393863(28),[109] 5.38[100]
Ellipses, ε = 100 0.0417[100] 0.0426[100] 5.513464(40),[109] 5.42[100]
Ellipses, ε = 200 0.021[112] 0.0212[112] 5.40[112]
Ellipses, ε = 1000 0.0043[100] 0.00431 5.624756(22),[109] 5.5
Superellipses, ε = 1, m = 1.5 0.671[102]
Superellipses, ε = 2.5, m = 1.5 0.599[102]
Superellipses, ε = 5, m = 1.5 0.469[102]
Superellipses, ε = 10, m = 1.5 0.322[102]
disco-rectangles, ε = 1.5 1.894 [108]
disco-rectangles, ε = 2 2.245 [108]
Aligned squares of side [math]\displaystyle{ \ell }[/math] 0.66675(2),[52] 0.66674349(3),[94] 0.66653(1),[113] 0.6666(4),[114] 0.668[101] 1.09884280(9),[94] 1.0982(3),[113] 1.098(1)[114] 1.09884280(9),[94] 1.0982(3),[113] 1.098(1)[114]
Randomly oriented squares 0.62554075(4),[94] 0.6254(2)[114] 0.625,[102] 0.9822723(1),[94] 0.9819(6)[114] 0.982278(14)[115] 0.9822723(1),[94] 0.9819(6)[114] 0.982278(14)[115]
Randomly oriented squares within angle [math]\displaystyle{ \pi/4 }[/math] 0.6255(1)[114] 0.98216(15)[114]
Rectangles, ε = 1.1 0.624870(7) 0.980484(19) 1.078532(21)[115]
Rectangles, ε = 2 0.590635(5) 0.893147(13) 1.786294(26)[115]
Rectangles, ε = 3 0.5405983(34) 0.777830(7) 2.333491(22)[115]
Rectangles, ε = 4 0.4948145(38) 0.682830(8) 2.731318(30)[115]
Rectangles, ε = 5 0.4551398(31), 0.451[102] 0.607226(6) 3.036130(28)[115]
Rectangles, ε = 10 0.3233507(25), 0.319[102] 0.3906022(37) 3.906022(37)[115]
Rectangles, ε = 20 0.2048518(22) 0.2292268(27) 4.584535(54)[115]
Rectangles, ε = 50 0.09785513(36) 0.1029802(4) 5.149008(20)[115]
Rectangles, ε = 100 0.0523676(6) 0.0537886(6) 5.378856(60)[115]
Rectangles, ε = 200 0.02714526(34) 0.02752050(35) 5.504099(69)[115]
Rectangles, ε = 1000 0.00559424(6) 0.00560995(6) 5.609947(60)[115]
Sticks (needles) of length [math]\displaystyle{ \ell }[/math] 5.63726(2),[116] 5.6372858(6),[94] 5.637263(11),[115] 5.63724(18) [117]
sticks with log-normal length dist. STD=0.5 4.756(3) [117]
sticks with correlated angle dist. s=0.5 6.6076(4) [117]
Power-law disks, x = 2.05 0.993(1)[118] 4.90(1) 0.0380(6)
Power-law disks, x = 2.25 0.8591(5)[118] 1.959(5) 0.06930(12)
Power-law disks, x = 2.5 0.7836(4)[118] 1.5307(17) 0.09745(11)
Power-law disks, x = 4 0.69543(6)[118] 1.18853(19) 0.18916(3)
Power-law disks, x = 5 0.68643(13)[118] 1.1597(3) 0.22149(8)
Power-law disks, x = 6 0.68241(8)[118] 1.1470(1) 0.24340(5)
Power-law disks, x = 7 0.6803(8)[118] 1.140(6) 0.25933(16)
Power-law disks, x = 8 0.67917(9)[118] 1.1368(5) 0.27140(7)
Power-law disks, x = 9 0.67856(12)[118] 1.1349(4) 0.28098(9)
Voids around disks of radius r 1 − Φc(disk) = 0.32355169(2),[94] 0.318(2),[119] 0.3261(6)[120]
2D continuum percolation with disks
2D continuum percolation with ellipses of aspect ratio 2

[math]\displaystyle{ \eta_c = \pi r^2 N / L^2 }[/math] equals critical total area for disks, where N is the number of objects and L is the system size.

[math]\displaystyle{ 4 \eta_c }[/math] gives the number of disk centers within the circle of influence (radius 2 r).

[math]\displaystyle{ r_c = L \sqrt{\frac{\eta_c}{\pi N}} }[/math] is the critical disk radius.

[math]\displaystyle{ \eta_c = \pi a b N / L^2 }[/math] for ellipses of semi-major and semi-minor axes of a and b, respectively. Aspect ratio [math]\displaystyle{ \epsilon = a / b }[/math] with [math]\displaystyle{ a \gt b }[/math].

[math]\displaystyle{ \eta_c = \ell m N / L^2 }[/math] for rectangles of dimensions [math]\displaystyle{ \ell }[/math] and [math]\displaystyle{ m }[/math]. Aspect ratio [math]\displaystyle{ \epsilon = \ell/m }[/math] with [math]\displaystyle{ \ell \gt m }[/math].

[math]\displaystyle{ \eta_c = \pi x N / (4 L^2 (x-2)) }[/math] for power-law distributed disks with [math]\displaystyle{ \hbox{Prob(radius}\ge R) = R^{-x} }[/math], [math]\displaystyle{ R \ge 1 }[/math].

[math]\displaystyle{ \phi_c = 1 - e^{-\eta_c} }[/math] equals critical area fraction.

For disks, Ref. [99] use [math]\displaystyle{ \phi_c = 1 - e^{-\pi x / 2} }[/math] where [math]\displaystyle{ x }[/math] is the density of disks of radius [math]\displaystyle{ 1/\sqrt{2} }[/math].

[math]\displaystyle{ n_c = \ell^2 N / L^2 }[/math] equals number of objects of maximum length [math]\displaystyle{ \ell = 2 a }[/math] per unit area.

For ellipses, [math]\displaystyle{ n_c = (4 \epsilon / \pi)\eta_c }[/math]

For void percolation, [math]\displaystyle{ \phi_c = e^{-\eta_c} }[/math] is the critical void fraction.

For more ellipse values, see [109][112]

For more rectangle values, see [115]

Both ellipses and rectangles belong to the superellipses, with [math]\displaystyle{ |x/a|^{2m}+|y/b|^{2m}=1 }[/math]. For more percolation values of superellipses, see.[102]

For the monodisperse particle systems, the percolation thresholds of concave-shaped superdisks are obtained as seen in [121]

For binary dispersions of disks, see [95][122][123]

Thresholds on 2D random and quasi-lattices

Voronoi diagram (solid lines) and its dual, the Delaunay triangulation (dotted lines), for a Poisson distribution of points
Delaunay triangulation
The Voronoi covering or line graph (dotted red lines) and the Voronoi diagram (black lines)
The Relative Neighborhood Graph (black lines)[124] superimposed on the Delaunay triangulation (black plus grey lines).
The Gabriel Graph, a subgraph of the Delaunay triangulation in which the circle surrounding each edge does not enclose any other points of the graph
Uniform Infinite Planar Triangulation, showing bond clusters. From[125]
Lattice z [math]\displaystyle{ \overline z }[/math] Site percolation threshold Bond percolation threshold
Relative neighborhood graph 2.5576 0.796(2)[124] 0.771(2)[124]
Voronoi tessellation 3 0.71410(2),[126] 0.7151*[69] 0.68,[127] 0.6670(1),[128] 0.6680(5),[129] 0.666931(5)[126]
Voronoi covering/medial 4 0.666931(2)[126][128] 0.53618(2)[126]
Randomized kagome/square-octagon, fraction r=​1⁄2 4 0.6599[16]
Penrose rhomb dual 4 0.6381(3)[66] 0.5233(2)[66]
Gabriel graph 4 0.6348(8),[130] 0.62[131] 0.5167(6),[130] 0.52[131]
Random-line tessellation, dual 4 0.586(2)[132]
Penrose rhomb 4 0.5837(3),[66] 0.0.5610(6) (weighted bonds)[133] 0.58391(1)[134] 0.483(5),[135] 0.4770(2)[66]
Octagonal lattice, "chemical" links (Ammann–Beenker tiling) 4 0.585[136] 0.48[136]
Octagonal lattice, "ferromagnetic" links 5.17 0.543[136] 0.40[136]
Dodecagonal lattice, "chemical" links 3.63 0.628[136] 0.54[136]
Dodecagonal lattice, "ferromagnetic" links 4.27 0.617[136] 0.495[136]
Delaunay triangulation 6 ​1⁄2[137] 0.3333(1)[128] 0.3326(5),[129] 0.333069(2)[126]
Uniform Infinite Planar Triangulation[138] 6 ​1⁄2 (2√3 – 1)/11 ≈ 0.2240[125][139]

*Theoretical estimate

Thresholds on 2D correlated systems

Assuming power-law correlations [math]\displaystyle{ C(r) \sim |r|^{-\alpha} }[/math]

lattice α Site percolation threshold Bond percolation threshold
square 3 0.561406(4)[140]
square 2 0.550143(5)[140]
square 0.1 0.508(4)[140]

Thresholds on slabs

h is the thickness of the slab, h × ∞ × ∞. Boundary conditions (b.c.) refer to the top and bottom planes of the slab.

Lattice h z [math]\displaystyle{ \overline z }[/math] Site percolation threshold Bond percolation threshold
simple cubic (open b.c.) 2 5 5 0.47424,[141] 0.4756[142]
bcc (open b.c.) 2 0.4155[142]
hcp (open b.c.) 2 0.2828[142]
diamond (open b.c.) 2 0.5451[142]
simple cubic (open b.c.) 3 0.4264[142]
bcc (open b.c.) 3 0.3531[142]
bcc (periodic b.c.) 3 0.21113018(38)[143]
hcp (open b.c.) 3 0.2548[142]
diamond (open b.c.) 3 0.5044[142]
simple cubic (open b.c.) 4 0.3997,[141] 0.3998[142]
bcc (open b.c.) 4 0.3232[142]
bcc (periodic b.c.) 4 0.20235168(59)[143]
hcp (open b.c.) 4 0.2405[142]
diamond (open b.c.) 4 0.4842[142]
simple cubic (periodic b.c.) 5 6 6 0.278102(5)[143]
simple cubic (open b.c.) 6 0.3708[142]
simple cubic (periodic b.c.) 6 6 6 0.272380(2)[143]
bcc (open b.c.) 6 0.2948[142]
hcp (open b.c.) 6 0.2261[142]
diamond (open b.c.) 6 0.4642[142]
simple cubic (periodic b.c.) 7 6 6 0.3459514(12)[143] 0.268459(1)[143]
simple cubic (open b.c.) 8 0.3557,[141] 0.3565[142]
simple cubic (periodic b.c.) 8 6 6 0.265615(5)[143]
bcc (open b.c.) 8 0.2811[142]
hcp (open b.c.) 8 0.2190[142]
diamond (open b.c.) 8 0.4549[142]
simple cubic (open b.c.) 12 0.3411[142]
bcc (open b.c.) 12 0.2688[142]
hcp (open b.c.) 12 0.2117[142]
diamond (open b.c.) 12 0.4456[142]
simple cubic (open b.c.) 16 0.3219,[141] 0.3339[142]
bcc (open b.c.) 16 0.2622[142]
hcp (open b.c.) 16 0.2086[142]
diamond (open b.c.) 16 0.4415[142]
simple cubic (open b.c.) 32 0.3219,[141]
simple cubic (open b.c.) 64 0.3165,[141]
simple cubic (open b.c.) 128 0.31398,[141]

Percolation in 3D

Lattice z [math]\displaystyle{ \overline z }[/math] filling factor* filling fraction* Site percolation threshold Bond percolation threshold
(10,3)-a oxide (or site-bond)[144] 23 32 2.4 0.748713(22)[144] = (pc,bond(10,3) – a)​1⁄2 = 0.742334(25)[145]
(10,3)-b oxide (or site-bond)[144] 23 32 2.4 0.233[146] 0.174 0.745317(25)[144] = (pc,bond(10,3) – b)​1⁄2 = 0.739388(22)[145]
silicon dioxide (diamond site-bond)[144] 4,22 2 ​2⁄3 0.638683(35)[144]
Modified (10,3)-b[147] 32,2 2 ​2⁄3 0.627[147]
(8,3)-a[145] 3 3 0.577962(33)[145] 0.555700(22)[145]
(10,3)-a[145] gyroid[148] 3 3 0.571404(40)[145] 0.551060(37)[145]
(10,3)-b[145] 3 3 0.565442(40)[145] 0.546694(33)[145]
cubic oxide (cubic site-bond)[144] 6,23 3.5 0.524652(50)[144]
bcc dual 4 0.4560(6)[149] 0.4031(6)[149]
ice Ih 4 4 π √3 / 16 = 0.340087 0.147 0.433(11)[150] 0.388(10)[151]
diamond (Ice Ic) 4 4 π √3 / 16 = 0.340087 0.1462332 0.4299(8),[152] 0.4299870(4),[153] 0.426+0.08
−0.02,[154] 0.4297(4) [155] 0.4301(4),[156] 0.428(4),[157] 0.425(15),[158] 0.425,[41][48] 0.436(12)[150] 		0.3895892(5),[153] 0.3893(2),[156] 0.3893(3),[155] 0.388(5),[158] 0.3886(5),[152] 0.388(5)[157] 0.390(11)[151]
diamond dual 6 ​2⁄3 0.3904(5)[149] 0.2350(5)[149]
3D kagome (covering graph of the diamond lattice) 6 π √2 / 12 = 0.37024 0.1442 0.3895(2)[159] =pc(site) for diamond dual and pc(bond) for diamond lattice[149] 0.2709(6)[149]
Bow-tie stack dual 5 ​1⁄3 0.3480(4)[38] 0.2853(4)[38]
honeycomb stack 5 5 0.3701(2)[38] 0.3093(2)[38]
octagonal stack dual 5 5 0.3840(4)[38] 0.3168(4)[38]
pentagonal stack 5 ​1⁄3 0.3394(4)[38] 0.2793(4)[38]
kagome stack 6 6 0.453450 0.1517 0.3346(4)[38] 0.2563(2)[38]
fcc dual 42,8 5 ​1⁄3 0.3341(5)[149] 0.2703(3)[149]
simple cubic 6 6 π / 6 = 0.5235988 0.1631574 0.307(10),[158] 0.307,[41] 0.3115(5),[160] 0.3116077(2),[161] 0.311604(6),[162] 0.311605(5),[163] 0.311600(5),[164] 0.3116077(4),[165] 0.3116081(13),[166] 0.3116080(4),[167] 0.3116060(48),[168] 0.3116004(35),[169] 0.31160768(15)[153] 0.247(5),[158] 0.2479(4),[152] 0.2488(2),[170] 0.24881182(10),[161] 0.2488125(25),[171] 0.2488126(5),[172]
hcp dual 44,82 5 ​1⁄3 0.3101(5)[149] 0.2573(3)[149]
dice stack 5,8 6 π √3 / 9 = 0.604600 0.1813 0.2998(4)[38] 0.2378(4)[38]
bow-tie stack 7 7 0.2822(6)[38] 0.2092(4)[38]
Stacked triangular / simple hexagonal 8 8 0.26240(5),[173] 0.2625(2),[174] 0.2623(2)[38] 0.18602(2),[173] 0.1859(2)[38]
octagonal (union-jack) stack 6,10 8 0.2524(6)[38] 0.1752(2)[38]
bcc 8 8 0.243(10),[158] 0.243,[41] 0.2459615(10),[167] 0.2460(3),[175] 0.2464(7),[152] 0.2458(2)[156] 0.178(5),[158] 0.1795(3),[152] 0.18025(15),[170] 0.1802875(10)[172]
simple cubic with 3NN (same as bcc) 8 8 0.2455(1),[176] 0.2457(7)[177]
fcc, D3 12 12 π / (3 √2) = 0.740480 0.147530 0.195,[41] 0.198(3),[178] 0.1998(6),[152] 0.1992365(10),[167] 0.19923517(20),[153] 0.1994(2),[156] 0.199236(4)[179] 0.1198(3),[152] 0.1201635(10)[172] 0.120169(2)[179]
hcp 12 12 π / (3 √2) = 0.740480 0.147545 0.195(5),[158] 0.1992555(10)[180] 0.1201640(10),[180] 0.119(2)[158]
La2−x Srx Cu O4 12 12 0.19927(2)[181]
simple cubic with 2NN (same as fcc) 12 12 0.1991(1)[176]
simple cubic with NN+4NN 12 12 0.15040(12),[182] 0.1503793(7)[183] 0.1068263(7)[184]
simple cubic with 3NN+4NN 14 14 0.20490(12)[182] 0.1012133(7)[184]
bcc NN+2NN (= sc(3,4) sc-3NN+4NN) 14 14 0.175,[41] 0.1686,(20)[185] 0.1759432(8) 0.0991(5),[185] 0.1012133(7),[45] 0.1759432(8) [45]
Nanotube fibers on FCC 14 14 0.1533(13)[186]
simple cubic with NN+3NN 14 14 0.1420(1)[176] 0.0920213(7)[184]
simple cubic with 2NN+4NN 18 18 0.15950(12)[182] 0.0751589(9)[184]
simple cubic with NN+2NN 18 18 0.137,[48] 0.136,[187] 0.1372(1),[176] 0.13735(5),[citation needed] 0.1373045(5)[45] 0.0752326(6) [184]
fcc with NN+2NN (=sc-2NN+4NN) 18 18 0.136,[41] 0.1361408(8)[45] 0.0751589(9) [45]
simple cubic with short-length correlation 6+ 6+ 0.126(1)[188]
simple cubic with NN+3NN+4NN 20 20 0.11920(12)[182] 0.0624379(9)[184]
simple cubic with 2NN+3NN 20 20 0.1036(1)[176] 0.0629283(7)[184]
simple cubic with NN+2NN+4NN 24 24 0.11440(12)[182] 0.0533056(6)[184]
simple cubic with 2NN+3NN+4NN 26 26 0.11330(12)[182] 0.0474609(9)
simple cubic with NN+2NN+3NN 26 26 0.097,[41] 0.0976(1),[176] 0.0976445(10), 0.0976444(6)[45] 0.0497080(10)[184]
bcc with NN+2NN+3NN 26 26 0.095,[48] 0.0959084(6)[45] 0.0492760(10)[45]
simple cubic with NN+2NN+3NN+4NN 32 32 0.10000(12),[182] 0.0801171(9)[45] 0.0392312(8)[184]
fcc with NN+2NN+3NN 42 42 0.061,[48] 0.0610(5),[187] 0.0618842(8)[45] 0.0290193(7) [45]
fcc with NN+2NN+3NN+4NN 54 54 0.0500(5)[187]
sc-1,2,3,4,5 simple cubic with NN+2NN+3NN+4NN+5NN 56 56 0.0461815(5)[45] 0.0210977(7)[45]
sc-1,...,6 (2x2x2 cube [51]) 80 80 0.0337049(9),[45] 0.03373(13)[51] 0.0143950(10)[45]
sc-1,...,7 92 92 0.0290800(10)[45] 0.0123632(8)[45]
sc-1,...,8 122 122 0.0218686(6)[45] 0.0091337(7)[45]
sc-1,...,9 146 146 0.0184060(10)[45] 0.0075532(8)[45]
sc-1,...,10 170 170 0.0064352(8)[45]
sc-1,...,11 178 178 0.0061312(8)[45]
sc-1,...,12 202 202 0.0053670(10)[45]
sc-1,...,13 250 250 0.0042962(8)[45]
3x3x3 cube 274 274 φc= 0.76564(1),[52] pc = 0.0098417(7),[52] 0.009854(6)[51]
4x4x4 cube 636 636 φc=0.76362(1),[52] pc = 0.0042050(2),[52] 0.004217(3)[51]
5x5x5 cube 1214 1250 φc=0.76044(2),[52] pc = 0.0021885(2),[52] 0.002185(4)[51]
6x6x6 cube 2056 2056 0.001289(2)[51]

Filling factor = fraction of space filled by touching spheres at every lattice site (for systems with uniform bond length only). Also called Atomic Packing Factor.

Filling fraction (or Critical Filling Fraction) = filling factor * pc(site).

NN = nearest neighbor, 2NN = next-nearest neighbor, 3NN = next-next-nearest neighbor, etc.

kxkxk cubes are cubes of occupied sites on a lattice, and are equivalent to extended-range percolation of a cube of length (2k+1), with edges and corners removed, with z = (2k+1)3-12(2k-1)-9 (center site not counted in z).

Question: the bond thresholds for the hcp and fcc lattice agree within the small statistical error. Are they identical, and if not, how far apart are they? Which threshold is expected to be bigger? Similarly for the ice and diamond lattices. See [189]

System polymer Φc
percolating excluded volume of athermal polymer matrix (bond-fluctuation model on cubic lattice) 0.4304(3)[190]



3D distorted lattices

Here, one distorts a regular lattice of unit spacing by moving vertices uniformly within the cube [math]\displaystyle{ (x-\alpha,x+\alpha),(y-\alpha,y+\alpha),(z-\alpha,z+\alpha) }[/math], and considers percolation when sites are within Euclidean distance [math]\displaystyle{ d }[/math] of each other.


Lattice [math]\displaystyle{ \overline z }[/math] [math]\displaystyle{ \alpha }[/math] [math]\displaystyle{ d }[/math] Site percolation threshold Bond percolation threshold
cubic 0.05 1.0 0.60254(3)[191]
0.1 1.00625 0.58688(4)[191]
0.15 1.025 0.55075(2)[191]
0.175 1.05 0.50645(5)[191]
0.2 1.1 0.44342(3)[191]



Overlapping shapes on 3D lattices

Site threshold is the number of overlapping objects per lattice site. The coverage φc is the net fraction of sites covered, and v is the volume (number of cubes). Overlapping cubes are given in the section on thresholds of 3D lattices. Here z is the coordination number to k-mers of either orientation, with [math]\displaystyle{ z=6k^2+18k-4 }[/math]

System k z Site coverage φc Site percolation threshold pc
1 x 2 dimer, cubic lattice 2 56 0.24542[51] 0.045847(2)[51]
1 x 3 trimer, cubic lattice 3 104 0.19578[51] 0.023919(9)[51]
1 x 4 stick, cubic lattice 4 164 0.16055[51] 0.014478(7)[51]
1 x 5 stick, cubic lattice 5 236 0.13488[51] 0.009613(8)[51]
1 x 6 stick, cubic lattice 6 320 0.11569[51] 0.006807(2)[51]
2 x 2 plaquette, cubic lattice 2 0.22710[51] 0.021238(2)[51]
3 x 3 plaquette, cubic lattice 3 0.18686[51] 0.007632(5)[51]
4 x 4 plaquette, cubic lattice 4 0.16159[51] 0.003665(3)[51]
5 x 5 plaquette, cubic lattice 5 0.14316[51] 0.002058(5)[51]
6 x 6 plaquette, cubic lattice 6 0.12900[51] 0.001278(5)[51]

The coverage is calculated from [math]\displaystyle{ p_c }[/math] by [math]\displaystyle{ \phi_c = 1-(1-p_c)^{3 k} }[/math] for sticks, and [math]\displaystyle{ \phi_c = 1-(1-p_c)^{3 k^2} }[/math] for plaquettes.

Dimer percolation in 3D

System Site percolation threshold Bond percolation threshold
Simple cubic 0.2555(1)[192]

Thresholds for 3D continuum models

All overlapping except for jammed spheres and polymer matrix.

System Φc ηc
Spheres of radius r 0.289,[193] 0.293,[194] 0.286,[195] 0.295.[101] 0.2895(5),[196] 0.28955(7),[197] 0.2896(7),[198] 0.289573(2),[199] 0.2896,[200] 0.2854,[201] 0.290,[202] 0.290[203] 0.3418(7),[196] 0.3438(13),[204] 0.341889(3),[199] 0.3360,[201] 0.34189(2) [113] [corrected], 0.341935(8),[205] 0.335,[206]
Oblate ellipsoids with major radius r and aspect ratio ​4⁄3 0.2831[201] 0.3328[201]
Prolate ellipsoids with minor radius r and aspect ratio ​3⁄2 0.2757,[200] 0.2795,[201] 0.2763[202] 0.3278[201]
Oblate ellipsoids with major radius r and aspect ratio 2 0.2537,[200] 0.2629,[201] 0.254[202] 0.3050[201]
Prolate ellipsoids with minor radius r and aspect ratio 2 0.2537,[200] 0.2618,[201] 0.25(2),[207] 0.2507[202] 0.3035,[201] 0.29(3)[207]
Oblate ellipsoids with major radius r and aspect ratio 3 0.2289[201] 0.2599[201]
Prolate ellipsoids with minor radius r and aspect ratio 3 0.2033,[200] 0.2244,[201] 0.20(2)[207] 0.2541,[201] 0.22(3)[207]
Oblate ellipsoids with major radius r and aspect ratio 4 0.2003[201] 0.2235[201]
Prolate ellipsoids with minor radius r and aspect ratio 4 0.1901,[201] 0.16(2)[207] 0.2108,[201] 0.17(3)[207]
Oblate ellipsoids with major radius r and aspect ratio 5 0.1757[201] 0.1932[201]
Prolate ellipsoids with minor radius r and aspect ratio 5 0.1627,[201] 0.13(2)[207] 0.1776,[201] 0.15(2)[207]
Oblate ellipsoids with major radius r and aspect ratio 10 0.0895,[200] 0.1058[201] 0.1118[201]
Prolate ellipsoids with minor radius r and aspect ratio 10 0.0724,[200] 0.08703,[201] 0.07(2)[207] 0.09105,[201] 0.07(2)[207]
Oblate ellipsoids with major radius r and aspect ratio 100 0.01248[201] 0.01256[201]
Prolate ellipsoids with minor radius r and aspect ratio 100 0.006949[201] 0.006973[201]
Oblate ellipsoids with major radius r and aspect ratio 1000 0.001275[201] 0.001276[201]
Oblate ellipsoids with major radius r and aspect ratio 2000 0.000637[201] 0.000637[201]
Spherocylinders with H/D = 1 0.2439(2)[198]
Spherocylinders with H/D = 4 0.1345(1)[198]
Spherocylinders with H/D = 10 0.06418(20)[198]
Spherocylinders with H/D = 50 0.01440(8)[198]
Spherocylinders with H/D = 100 0.007156(50)[198]
Spherocylinders with H/D = 200 0.003724(90)[198]
Aligned cylinders 0.2819(2)[208] 0.3312(1)[208]
Aligned cubes of side [math]\displaystyle{ \ell = 2 a }[/math] 0.2773(2)[114] 0.27727(2),[52] 0.27730261(79)[168] 0.3247(3),[113] 0.3248(3),[114] 0.32476(4)[208] 0.324766(1)[168]
Randomly oriented icosahedra 0.3030(5)[209]
Randomly oriented dodecahedra 0.2949(5)[209]
Randomly oriented octahedra 0.2514(6)[209]
Randomly oriented cubes of side [math]\displaystyle{ \ell = 2 a }[/math] 0.2168(2)[114] 0.2174,[200] 0.2444(3),[114] 0.2443(5)[209]
Randomly oriented tetrahedra 0.1701(7)[209]
Randomly oriented disks of radius r (in 3D) 0.9614(5)[210]
Randomly oriented square plates of side [math]\displaystyle{ \sqrt{\pi} r }[/math] 0.8647(6)[210]
Randomly oriented triangular plates of side [math]\displaystyle{ \sqrt{2 \pi} /3^{1/4} r }[/math] 0.7295(6)[210]
Jammed spheres (average z = 6) 0.183(3),[211] 0.1990,[212] see also contact network of jammed spheres below. 0.59(1)[211] (volume fraction of all spheres)

[math]\displaystyle{ \eta_c = (4/3) \pi r^3 N / L^3 }[/math] is the total volume (for spheres), where N is the number of objects and L is the system size.

[math]\displaystyle{ \phi_c = 1 - e^{-\eta_c} }[/math] is the critical volume fraction, valid for overlapping randomly placed objects.

For disks and plates, these are effective volumes and volume fractions.

For void ("Swiss-Cheese" model), [math]\displaystyle{ \phi_c = e^{-\eta_c} }[/math] is the critical void fraction.

For more results on void percolation around ellipsoids and elliptical plates, see.[213]

For more ellipsoid percolation values see.[201]

For spherocylinders, H/D is the ratio of the height to the diameter of the cylinder, which is then capped by hemispheres. Additional values are given in.[198]

For superballs, m is the deformation parameter, the percolation values are given in.,[214][215] In addition, the thresholds of concave-shaped superballs are also determined in [121]

For cuboid-like particles (superellipsoids), m is the deformation parameter, more percolation values are given in.[200]

Void percolation in 3D

Void percolation refers to percolation in the space around overlapping objects. Here [math]\displaystyle{ \phi_c }[/math] refers to the fraction of the space occupied by the voids (not of the particles) at the critical point, and is related to [math]\displaystyle{ \eta_c }[/math] by [math]\displaystyle{ \phi_c = e^{-\eta_c} }[/math]. [math]\displaystyle{ \eta_c }[/math] is defined as in the continuum percolation section above.

System Φc ηc
Voids around disks of radius r 22.86(2)[213]
Voids around randomly oriented tetrahedra 0.0605(6)[216]
Voids around oblate ellipsoids of major radius r and aspect ratio 32 0.5308(7)[217] 0.6333[217]
Voids around oblate ellipsoids of major radius r and aspect ratio 16 0.3248(5)[217] 1.125[217]
Voids around oblate ellipsoids of major radius r and aspect ratio 10 1.542(1)[213]
Voids around oblate ellipsoids of major radius r and aspect ratio 8 0.1615(4)[217] 1.823[217]
Voids around oblate ellipsoids of major radius r and aspect ratio 4 0.0711(2)[217] 2.643,[217] 2.618(5)[213]
Voids around oblate ellipsoids of major radius r and aspect ratio 2 3.239(4) [213]
Voids around prolate ellipsoids of aspect ratio 8 0.0415(7)[218]
Voids around prolate ellipsoids of aspect ratio 6 0.0397(7)[218]
Voids around prolate ellipsoids of aspect ratio 4 0.0376(7)[218]
Voids around prolate ellipsoids of aspect ratio 3 0.03503(50)[218]
Voids around prolate ellipsoids of aspect ratio 2 0.0323(5)[218]
Voids around aligned square prisms of aspect ratio 2 0.0379(5) [219]
Voids around randomly oriented square prisms of aspect ratio 20 0.0534(4) [219]
Voids around randomly oriented square prisms of aspect ratio 15 0.0535(4) [219]
Voids around randomly oriented square prisms of aspect ratio 10 0.0524(5) [219]
Voids around randomly oriented square prisms of aspect ratio 8 0.0523(6) [219]
Voids around randomly oriented square prisms of aspect ratio 7 0.0519(3) [219]
Voids around randomly oriented square prisms of aspect ratio 6 0.0519(5) [219]
Voids around randomly oriented square prisms of aspect ratio 5 0.0515(7) [219]
Voids around randomly oriented square prisms of aspect ratio 4 0.0505(7) [219]
Voids around randomly oriented square prisms of aspect ratio 3 0.0485(11) [219]
Voids around randomly oriented square prisms of aspect ratio 5/2 0.0483(8) [219]
Voids around randomly oriented square prisms of aspect ratio 2 0.0465(7) [219]
Voids around randomly oriented square prisms of aspect ratio 3/2 0.0461(14) [219]
Voids around hemispheres 0.0455(6)[220]
Voids around aligned tetrahedra 0.0605(6)[216]
Voids around randomly oriented tetrahedra 0.0605(6)[216]
Voids around aligned cubes 0.036(1),[52] 0.0381(3)[216]
Voids around randomly oriented cubes 0.0452(6),[216] 0.0449(5)[219]
Voids around aligned octahedra 0.0407(3)[216]
Voids around randomly oriented octahedra 0.0398(5)[216]
Voids around aligned dodecahedra 0.0356(3)[216]
Voids around randomly oriented dodecahedra 0.0360(3)[216]
Voids around aligned icosahedra 0.0346(3)[216]
Voids around randomly oriented icosahedra 0.0336(7)[216]
Voids around spheres 0.034(7),[221] 0.032(4),[222] 0.030(2),[119] 0.0301(3),[223] 0.0294,[218] 0.0300(3),[224] 0.0317(4),[225] 0.0308(5)[220] 0.0301(1),[217] 0.0301(1)[216] 3.506(8),[224] 3.515(6),[213] 3.510(2)[105]

Thresholds on 3D random and quasi-lattices

Lattice z [math]\displaystyle{ \overline z }[/math] Site percolation threshold Bond percolation threshold
Contact network of packed spheres 6 0.310(5),[211] 0.287(50),[226] 0.3116(3),[212]
Random-plane tessellation, dual 6 0.290(7)[227]
Icosahedral Penrose 6 0.285[228] 0.225[228]
Penrose w/2 diagonals 6.764 0.271[228] 0.207[228]
Penrose w/8 diagonals 12.764 0.188[228] 0.111[228]
Voronoi network 15.54 0.1453(20)[185] 0.0822(50)[185]

Thresholds for other 3D models

Lattice z [math]\displaystyle{ \overline z }[/math] Site percolation threshold Critical coverage fraction [math]\displaystyle{ \phi_c }[/math] Bond percolation threshold
Drilling percolation, simple cubic lattice* 6 6 0.6345(3),[229] 0.6339(5),[230] 0.633965(15)[231] 0.25480
Drill in z direction on cubic lattice, remove single sites 6 6 0.592746 (columns), 0.4695(10) (sites)[232] 0.2784
Random tube model, simple cubic lattice† 0.231456(6)[233]

[math]\displaystyle{ ^* }[/math] In drilling percolation, the site threshold [math]\displaystyle{ p_c }[/math] represents the fraction of columns in each direction that have not been removed, and [math]\displaystyle{ \phi_c=p_c^3 }[/math]. For the 1d drilling, we have [math]\displaystyle{ \phi_c = p_c }[/math](columns) [math]\displaystyle{ p_c }[/math](sites).

† In tube percolation, the bond threshold represents the value of the parameter [math]\displaystyle{ \mu }[/math] such that the probability of putting a bond between neighboring vertical tube segments is [math]\displaystyle{ 1-e^{-\mu h_i} }[/math], where [math]\displaystyle{ h_i }[/math] is the overlap height of two adjacent tube segments.[233]

Thresholds in different dimensional spaces

Continuum models in higher dimensions

d System Φc ηc
4 Overlapping hyperspheres 0.1223(4)[113] 0.1300(13),[204] 0.1304(5)[113]
4 Aligned hypercubes 0.1132(5),[113] 0.1132348(17) [168] 0.1201(6)[113]
4 Voids around hyperspheres 0.00211(2)[120] 6.161(10)[120] 6.248(2),[105]
5 Overlapping hyperspheres 0.0544(6),[204] 0.05443(7)[113]
5 Aligned hypercubes 0.04900(7),[113] 0.0481621(13)[168] 0.05024(7)[113]
5 Voids around hyperspheres 1.26(6)x10−4[120] 8.98(4),[120] 9.170(8)[105]
6 Overlapping hyperspheres 0.02391(31),[204] 0.02339(5)[113]
6 Aligned hypercubes 0.02082(8),[113] 0.0213479(10)[168] 0.02104(8)[113]
6 Voids around hyperspheres 8.0(6)x10−6 [120] 11.74(8),[120] 12.24(2),[105]
7 Overlapping hyperspheres 0.01102(16),[204] 0.01051(3)[113]
7 Aligned hypercubes 0.00999(5),[113] 0.0097754(31)[168] 0.01004(5)[113]
7 Voids around hyperspheres 15.46(5)[105]
8 Overlapping hyperspheres 0.00516(8),[204] 0.004904(6)[113]
8 Aligned hypercubes 0.004498(5)[113]
8 Voids around hyperspheres 18.64(8)[105]
9 Overlapping hyperspheres 0.002353(4)[113]
9 Aligned hypercubes 0.002166(4)[113]
9 Voids around hyperspheres 22.1(4)[105]
10 Overlapping hyperspheres 0.001138(3)[113]
10 Aligned hypercubes 0.001058(4)[113]
11 Overlapping hyperspheres 0.0005530(3)[113]
11 Aligned hypercubes 0.0005160(3)[113]

[math]\displaystyle{ \eta_c = (\pi^{d/2}/ \Gamma[d/2 + 1]) r^d N / L^d. }[/math]

In 4d, [math]\displaystyle{ \eta_c = (1/2) \pi^2 r^4 N / L^4 }[/math].

In 5d, [math]\displaystyle{ \eta_c = (8/15) \pi^2 r^5 N / L^5 }[/math].

In 6d, [math]\displaystyle{ \eta_c = (1/6) \pi^3 r^6 N / L^6 }[/math].

[math]\displaystyle{ \phi_c = 1 - e^{-\eta_c} }[/math] is the critical volume fraction, valid for overlapping objects.

For void models, [math]\displaystyle{ \phi_c = e^{-\eta_c} }[/math] is the critical void fraction, and [math]\displaystyle{ \eta_c }[/math] is the total volume of the overlapping objects

Thresholds on hypercubic lattices

d z Site thresholds Bond thresholds
4 8 0.198(1)[234] 0.197(6),[235] 0.1968861(14),[236] 0.196889(3),[237] 0.196901(5),[238] 0.19680(23),[239] 0.1968904(65),[168] 0.19688561(3)[240] 0.1600(1),[241] 0.16005(15),[170] 0.1601314(13),[236] 0.160130(3),[237] 0.1601310(10),[171] 0.1601312(2),[242] 0.16013122(6)[240]
5 10 0.141(1),0.198(1)[234] 0.141(3),[235] 0.1407966(15),[236] 0.1407966(26),[168] 0.14079633(4)[240] 0.1181(1),[241] 0.118(1),[243] 0.11819(4),[170] 0.118172(1),[236] 0.1181718(3)[171] 0.11817145(3)[240]
6 12 0.106(1),[234] 0.108(3),[235] 0.109017(2),[236] 0.1090117(30),[168] 0.109016661(8)[240] 0.0943(1),[241] 0.0942(1),[244] 0.0942019(6),[236] 0.09420165(2)[240]
7 14 0.05950(5),[244] 0.088939(20),[245] 0.0889511(9),[236] 0.0889511(90),[168] 0.088951121(1),[240] 0.0787(1),[241] 0.078685(30),[244] 0.0786752(3),[236] 0.078675230(2)[240]
8 16 0.0752101(5),[236] 0.075210128(1)[240] 0.06770(5),[244] 0.06770839(7),[236] 0.0677084181(3)[240]
9 18 0.0652095(3),[236] 0.0652095348(6)[240] 0.05950(5),[244] 0.05949601(5),[236] 0.0594960034(1)[240]
10 20 0.0575930(1),[236] 0.0575929488(4)[240] 0.05309258(4),[236] 0.0530925842(2)[240]
11 22 0.05158971(8),[236] 0.0515896843(2)[240] 0.04794969(1),[236] 0.04794968373(8)[240]
12 24 0.04673099(6),[236] 0.0467309755(1)[240] 0.04372386(1),[236] 0.04372385825(10)[240]
13 26 0.04271508(8),[236] 0.04271507960(10)[240] 0.04018762(1),[236] 0.04018761703(6)[240]

For thresholds on high dimensional hypercubic lattices, we have the asymptotic series expansions [235] [243] [246]

[math]\displaystyle{ p_c^\mathrm{site}(d)=\sigma^{-1}+\frac{3}{2}\sigma^{-2}+\frac{15}{4}\sigma^{-3}+\frac{83}{4}\sigma^{-4}+\frac{6577}{48}\sigma^{-5}+\frac{119077}{96}\sigma^{-6}+{\mathcal O}(\sigma^{-7}) }[/math]

[math]\displaystyle{ p_c^\mathrm{bond}(d)=\sigma^{-1}+\frac{5}{2}\sigma^{-3}+\frac{15}{2}\sigma^{-4}+57\sigma^{-5}+\frac{4855}{12}\sigma^{-6}+{\mathcal O}(\sigma^{-7}) }[/math]

where [math]\displaystyle{ \sigma = 2 d - 1 }[/math]. For 13-dimensional bond percolation, for example, the error with the measured value is less than 10-6, and these formulas can be useful for higher-dimensional systems.

Thresholds in other higher-dimensional lattices

d lattice z Site thresholds Bond thresholds
4 diamond 5 0.2978(2)[156] 0.2715(3)[156]
4 kagome 8 0.2715(3)[159] 0.177(1) [156]
4 bcc 16 0.1037(3)[156] 0.074(1),[156] 0.074212(1)[242]
4 fcc, D4, hypercubic 2NN 24 0.0842(3),[156] 0.08410(23),[239] 0.0842001(11)[179] 0.049(1),[156] 0.049517(1),[242] 0.0495193(8)[179]
4 hypercubic NN+2NN 32 0.06190(23),[239] 0.0617731(19)[247] 0.035827(1),[242] 0.0338047(27)[247]
4 hypercubic 3NN 32 0.04540(23)[239]
4 hypercubic NN+3NN 40 0.04000(23)[239] 0.0271892(22)[247]
4 hypercubic 2NN+3NN 56 0.03310(23)[239] 0.0194075(15)[247]
4 hypercubic NN+2NN+3NN 64 0.03190(23),[239] 0.0319407(13)[247] 0.0171036(11)[247]
4 hypercubic NN+2NN+3NN+4NN 88 0.0231538(12)[247] 0.0122088(8)[247]
4 hypercubic NN+...+5NN 136 0.0147918(12)[247] 0.0077389(9)[247]
4 hypercubic NN+...+6NN 232 0.0088400(10)[247] 0.0044656(11)[247]
4 hypercubic NN+...+7NN 296 0.0070006(6)[247] 0.0034812(7)[247]
4 hypercubic NN+...+8NN 320 0.0064681(9)[247] 0.0032143(8)[247]
4 hypercubic NN+...+9NN 424 0.0048301(9)[247] 0.0024117(7)[247]
5 diamond 6 0.2252(3)[156] 0.2084(4)[159]
5 kagome 10 0.2084(4)[159] 0.130(2)[156]
5 bcc 32 0.0446(4)[156] 0.033(1)[156]
5 fcc, D5, hypercubic 2NN 40 0.0431(3),[156] 0.0435913(6)[179] 0.026(2),[156] 0.0271813(2)[179]
6 diamond 7 0.1799(5)[156] 0.1677(7)[159]
6 kagome 12 0.1677(7)[159]
6 fcc, D6 60 0.0252(5),[156] 0.02602674(12)[179] 0.01741556(5)[179]
6 bcc 64 0.0199(5)[156]
6 E6[179] 72 0.02194021(14)[179] 0.01443205(8)[179]
7 fcc, D7 84 0.01716730(5)[179] 0.012217868(13)[179]
7 E7[179] 126 0.01162306(4)[179] 0.00808368(2)[179]
8 fcc, D8 112 0.01215392(4)[179] 0.009081804(6)[179]
8 E8[179] 240 0.00576991(2)[179] 0.004202070(2)[179]
9 fcc, D9 144 0.00905870(2)[179] 0.007028457(3)[179]
9 [math]\displaystyle{ \Lambda_9 }[/math][179] 272 0.00480839(2)[179] 0.0037006865(11)[179]
10 fcc, D10 180 0.007016353(9)[179] 0.005605579(6)[179]
11 fcc, D11 220 0.005597592(4)[179] 0.004577155(3)[179]
12 fcc, D12 264 0.004571339(4)[179] 0.003808960(2)[179]
13 fcc, D13 312 0.003804565(3)[179] 0.0032197013(14)[179]

Thresholds in one-dimensional long-range percolation

Long-range bond percolation model. The lines represent the possible bonds with width decreasing as the connection probability decreases (left panel). An instance of the model together with the clusters generated (right panel).

In a one-dimensional chain we establish bonds between distinct sites [math]\displaystyle{ i }[/math] and [math]\displaystyle{ j }[/math] with probability [math]\displaystyle{ p=\frac{C}{|i-j|^{1+\sigma}} }[/math] decaying as a power-law with an exponent [math]\displaystyle{ \sigma\gt 0 }[/math]. Percolation occurs[248][249] at a critical value [math]\displaystyle{ C_c\lt 1 }[/math] for [math]\displaystyle{ \sigma\lt 1 }[/math]. The numerically determined percolation thresholds are given by:[250]

[math]\displaystyle{ \sigma }[/math] [math]\displaystyle{ C_c }[/math] Critical thresholds [math]\displaystyle{ C_c }[/math] as a function of [math]\displaystyle{ \sigma }[/math].[250]
The dotted line is the rigorous lower bound.[248]
0.1 0.047685(8) LR 1d percolation wiki.png
0.2 0.093211(16)
0.3 0.140546(17)
0.4 0.193471(15)
0.5 0.25482(5)
0.6 0.327098(6)
0.7 0.413752(14)
0.8 0.521001(14)
0.9 0.66408(7)

Thresholds on hyperbolic, hierarchical, and tree lattices

In these lattices there may be two percolation thresholds: the lower threshold is the probability above which infinite clusters appear, and the upper is the probability above which there is a unique infinite cluster.

Visualization of a triangular hyperbolic lattice {3,7} projected on the Poincaré disk (red bonds). Green bonds show dual-clusters on the {7,3} lattice[251]
Depiction of the non-planar Hanoi network HN-NP[252]
Lattice z [math]\displaystyle{ \overline z }[/math] Site percolation threshold Bond percolation threshold
Lower Upper Lower Upper
{3,7} hyperbolic 7 7 0.26931171(7),[253] 0.20[254] 0.73068829(7),[253] 0.73(2)[254] 0.20,[255] 0.1993505(5)[253] 0.37,[255] 0.4694754(8)[253]
{3,8} hyperbolic 8 8 0.20878618(9)[253] 0.79121382(9)[253] 0.1601555(2)[253] 0.4863559(6)[253]
{3,9} hyperbolic 9 9 0.1715770(1)[253] 0.8284230(1)[253] 0.1355661(4)[253] 0.4932908(1)[253]
{4,5} hyperbolic 5 5 0.29890539(6)[253] 0.8266384(5)[253] 0.27,[255] 0.2689195(3)[253] 0.52,[255] 0.6487772(3) [253]
{4,6} hyperbolic 6 6 0.22330172(3)[253] 0.87290362(7)[253] 0.20714787(9)[253] 0.6610951(2)[253]
{4,7} hyperbolic 7 7 0.17979594(1)[253] 0.89897645(3)[253] 0.17004767(3)[253] 0.66473420(4)[253]
{4,8} hyperbolic 8 8 0.151035321(9)[253] 0.91607962(7)[253] 0.14467876(3)[253] 0.66597370(3)[253]
{4,9} hyperbolic 8 8 0.13045681(3)[253] 0.92820305(3)[253] 0.1260724(1)[253] 0.66641596(2)[253]
{5,5} hyperbolic 5 5 0.26186660(5)[253] 0.89883342(7)[253] 0.263(10),[256] 0.25416087(3)[253] 0.749(10)[256] 0.74583913(3)[253]
{7,3} hyperbolic 3 3 0.54710885(10)[253] 0.8550371(5),[253] 0.86(2)[254] 0.53,[255] 0.551(10),[256] 0.5305246(8)[253] 0.72,[255] 0.810(10),[256] 0.8006495(5)[253]
{∞,3} Cayley tree 3 3 ​1⁄2 ​1⁄2[255] 1[255]
Enhanced binary tree (EBT) 0.304(1),[257] 0.306(10),[256] (√13 − 3)/2 = 0.302776[258] 0.48,[255] 0.564(1),[257] 0.564(10),[256] ​1⁄2[258]
Enhanced binary tree dual 0.436(1),[257] 0.452(10)[256] 0.696(1),[257] 0.699(10)[256]
Non-Planar Hanoi Network (HN-NP) 0.319445[252] 0.381996[252]
Cayley tree with grandparents 8 0.158656326[259]

Note: {m,n} is the Schläfli symbol, signifying a hyperbolic lattice in which n regular m-gons meet at every vertex

For bond percolation on {P,Q}, we have by duality [math]\displaystyle{ p_{c,\ell}(P,Q) + p_{c,u}(Q,P) = 1 }[/math]. For site percolation, [math]\displaystyle{ p_{c,\ell}(3,Q) + p_{c,u}(3,Q) = 1 }[/math] because of the self-matching of triangulated lattices.

Cayley tree (Bethe lattice) with coordination number [math]\displaystyle{ z : p_c = 1 / ( z - 1 ) }[/math]

Thresholds for directed percolation

(1+1)D Kagome Lattice
(1+1)D Square Lattice
(1+1)D Triangular Lattice
(2+1)D SC Lattice
(2+1)D BCC Lattice
Lattice z Site percolation threshold Bond percolation threshold
(1+1)-d honeycomb 1.5 0.8399316(2),[260] 0.839933(5),[261] [math]\displaystyle{ = \sqrt{p_c({\mathrm{site}})} }[/math] of (1+1)-d sq. 0.8228569(2),[260] 0.82285680(6)[260]
(1+1)-d kagome 2 0.7369317(2),[260] 0.73693182(4)[262] 0.6589689(2),[260] 0.65896910(8)[260]
(1+1)-d square, diagonal 2 0.705489(4),[263] 0.705489(4),[264] 0.70548522(4),[265] 0.70548515(20),[262] 0.7054852(3),[260] 0.644701(2),[266] 0.644701(1),[267] 0.644701(1),[263] 0.6447006(10),[261] 0.64470015(5),[268] 0.644700185(5),[265] 0.6447001(2),[260] 0.643(2)[269]
(1+1)-d triangular 3 0.595646(3),[263] 0.5956468(5),[268] 0.5956470(3)[260] 0.478018(2),[263] 0.478025(1),[268] 0.4780250(4)[260] 0.479(3)[269]
(2+1)-d simple cubic, diagonal planes 3 0.43531(1),[270] 0.43531411(10)[260] 0.382223(7),[270] 0.38222462(6)[260] 0.383(3)[269]
(2+1)-d square nn (= bcc) 4 0.3445736(3),[271] 0.344575(15)[272] 0.3445740(2)[260] 0.2873383(1),[273] 0.287338(3)[270] 0.28733838(4)[260] 0.287(3)[269]
(2+1)-d fcc 0.199(2))[269]
(3+1)-d hypercubic, diagonal 4 0.3025(10),[274] 0.30339538(5) [260] 0.26835628(5),[260] 0.2682(2)[269]
(3+1)-d cubic, nn 6 0.2081040(4)[271] 0.1774970(5)[171]
(3+1)-d bcc 8 0.160950(30),[272] 0.16096128(3)[260] 0.13237417(2)[260]
(4+1)-d hypercubic, diagonal 5 0.23104686(3)[260] 0.20791816(2),[260] 0.2085(2)[269]
(4+1)-d hypercubic, nn 8 0.1461593(2),[271] 0.1461582(3)[275] 0.1288557(5)[171]
(4+1)-d bcc 16 0.075582(17),[272] 0.0755850(3),[275] 0.07558515(1)[260] 0.063763395(5)[260]
(5+1)-d hypercubic, diagonal 6 0.18651358(2)[260] 0.170615155(5),[260] 0.1714(1) [269]
(5+1)-d hypercubic, nn 10 0.1123373(2)[271] 0.1016796(5)[171]
(5+1)-d hypercubic bcc 32 0.035967(23),[272] 0.035972540(3)[260] 0.0314566318(5)[260]
(6+1)-d hypercubic, diagonal 7 0.15654718(1)[260] 0.145089946(3),[260] 0.1458[269]
(6+1)-d hypercubic, nn 12 0.0913087(2)[271] 0.0841997(14)[171]
(6+1)-d hypercubic bcc 64 0.017333051(2)[260] 0.01565938296(10)[260]
(7+1)-d hypercubic, diagonal 8 0.135004176(10)[260] 0.126387509(3),[260] 0.1270(1) [269]
(7+1)-d hypercubic,nn 14 0.07699336(7)[271] 0.07195(5)[171]
(7+1)-d bcc 128 0.008 432 989(2)[260] 0.007 818 371 82(6)[260]

nn = nearest neighbors. For a (d + 1)-dimensional hypercubic system, the hypercube is in d dimensions and the time direction points to the 2D nearest neighbors.


Directed percolation with multiple neighbors

Lattice z Site percolation threshold Bond percolation threshold
(1+1)-d square with 3 NN 3 0.4395(3),[276]

Site-Bond Directed Percolation

p_b = bond threshold

p_s = site threshold

Site-bond percolation is equivalent to having different probabilities of connections:

P_0 = probability that no sites are connected

P_2 = probability that exactly one descendant is connected to the upper vertex (two connected together)

P_3 = probability that both descendants are connected to the original vertex (all three connected together)

Formulas:

P_0 = (1-p_s) + p_s(1-p_b)^2

P_2 = p_s p_b (1-p_b)

P_3 = p_s p_b^2

P_0 + 2P_2 + P_3 = 1

Lattice z p_s p_b P_0 P_2 P_3
(1+1)-d square [277] 3 0.644701 1 0.126237 0.229062 0.415639
0.7 0.93585 0.148376 0.196529 0.458567
0.75 0.88565 0.169703 0.166059 0.498178
0.8 0.84135 0.192304 0.134616 0.538464
0.85 0.80190 0.216143 0.102242 0.579373
0.9 0.76645 0.241215 0.068981 0.620825
0.95 0.73450 0.267336 0.034889 0.662886
1 0.705489 0.294511 0 0.705489

Exact critical manifolds of inhomogeneous systems

Inhomogeneous triangular lattice bond percolation[20]

[math]\displaystyle{ 1 - p_1 - p_2 - p_3 + p_1 p_2 p_3 = 0 }[/math]

Inhomogeneous honeycomb lattice bond percolation = kagome lattice site percolation[20]

[math]\displaystyle{ 1 - p_1 p_2 - p_1 p_3 - p_2 p_3+ p_1 p_2 p_3 = 0 }[/math]

Inhomogeneous (3,12^2) lattice, site percolation[7][278]

[math]\displaystyle{ 1 - 3(s_1s_2)^2 + (s_1s_2)^3 = 0, }[/math] or [math]\displaystyle{ s_1 s_2 = 1 - 2 \sin(\pi/18) }[/math]

Inhomogeneous union-jack lattice, site percolation with probabilities [math]\displaystyle{ p_1, p_2, p_3, p_4 }[/math][279]

[math]\displaystyle{ p_3 = 1 - p_1; \qquad p_4 = 1 - p_2 }[/math]

Inhomogeneous martini lattice, bond percolation[73][280]

[math]\displaystyle{ 1 - (p_1 p_2 r_3 + p_2 p_3 r_1 + p_1 p_3 r_2) - (p_1 p_2 r_1 r_2 + p_1 p_3 r_1 r_3 + p_2 p_3 r_2 r_3) + p_1 p_2 p_3 ( r_1 r_2 + r_1 r_3 + r_2 r_3) + r_1 r_2 r_3 (p_1 p_2 + p_1 p_3 + p_2 p_3) - 2 p_1 p_2 p_3 r_1 r_2 r_3 = 0 }[/math]

Inhomogeneous martini lattice, site percolation. r = site in the star

[math]\displaystyle{ 1 - r (p_1 p_2 + p_1 p_3 + p_2 p_3 - p_1 p_2 p_3) = 0 }[/math]

Inhomogeneous martini-A (3–7) lattice, bond percolation. Left side (top of "A" to bottom): [math]\displaystyle{ r_2,\ p_1 }[/math]. Right side: [math]\displaystyle{ r_1, \ p_2 }[/math]. Cross bond: [math]\displaystyle{ \ r_3 }[/math].

[math]\displaystyle{ 1 - p_1 r_2 - p_2 r_1 - p_1 p_2 r_3 - p_1 r_1 r_3 - p_2 r_2 r_3 + p_1 p_2 r_1 r_3 + p_1 p_2 r_2 r_3 + p_1 r_1 r_2 r_3+ p_2 r_1 r_2 r_3 - p_1 p_2 r_1 r_2 r_3 = 0 }[/math]

Inhomogeneous martini-B (3–5) lattice, bond percolation

Inhomogeneous martini lattice with outside enclosing triangle of bonds, probabilities [math]\displaystyle{ y, x, z }[/math] from inside to outside, bond percolation[280]

[math]\displaystyle{ 1 - 3 z + z^3-(1-z^2) [3 x^2 y (1 + y - y^2)(1 + z) + x^3 y^2 (3 - 2 y)(1 + 2 z) ] = 0 }[/math]

Inhomogeneous checkerboard lattice, bond percolation[57][93]

[math]\displaystyle{ 1 - (p_1 p_2 + p_1 p_3 + p_1 p_4 + p_2 p_3 + p_2 p_4 + p_3 p_4) + p_1 p_2 p_3 + p_1 p_2 p_4 + p_1 p_3 p_4 + p_2 p_3 p_4 = 0 }[/math]

Inhomogeneous bow-tie lattice, bond percolation[56][93]

[math]\displaystyle{ 1 - (p_1 p_2 + p_1 p_3 + p_1 p_4 + p_2 p_3 + p_2 p_4 + p_3 p_4) + p_1 p_2 p_3 + p_1 p_2 p_4 + p_1 p_3 p_4 + p_2 p_3 p_4 - u(1 - p_1 p_2 - p_3 p_4 + p_1 p_2 p_3 p_4) = 0 }[/math]

where [math]\displaystyle{ p_1, p_2, p_3, p_4 }[/math] are the four bonds around the square and [math]\displaystyle{ u }[/math] is the diagonal bond connecting the vertex between bonds [math]\displaystyle{ p_4, p_1 }[/math] and [math]\displaystyle{ p_2, p_3 }[/math].

See also


References

  1. ↑ Stauffer, Dietrich; Aharony, Amnon (2003). Introduction to percolation theory (Rev. 2nd ed.). London: Taylor & Francis. ISBN 978-0-7484-0253-3. 
  2. ↑ Kasteleyn, P. W.; Fortuin, C. M. (1969). "Phase transitions in lattice systems with random local properties". Journal of the Physical Society of Japan Supplement 26: 11–14. Bibcode: 1969JPSJS..26...11K. 
  3. ↑ 3.0 3.1 3.2 3.3 3.4 Grünbaum, Branko; Shephard, G. C. (1987). Tilings and Patterns. New York: W. H. Freeman. ISBN 978-0-7167-1193-3. https://archive.org/details/isbn_0716711931. 
  4. ↑ Berchenko, Yakir; Artzy-Randrup, Yael; Teicher, Mina; Stone, Lewi (2009-03-30). "Emergence and Size of the Giant Component in Clustered Random Graphs with a Given Degree Distribution" (in en). Physical Review Letters 102 (13): 138701. doi:10.1103/PhysRevLett.102.138701. ISSN 0031-9007. PMID 19392410. Bibcode: 2009PhRvL.102m8701B. https://link.aps.org/doi/10.1103/PhysRevLett.102.138701. 
  5. ↑ Li, Ming; Liu, Run-Ran; Lü, Linyuan; Hu, Mao-Bin; Xu, Shuqi; Zhang, Yi-Cheng (2021-04-25). "Percolation on complex networks: Theory and application" (in en). Physics Reports 907: 1–68. doi:10.1016/j.physrep.2020.12.003. ISSN 0370-1573. Bibcode: 2021PhR...907....1L. https://www.sciencedirect.com/science/article/pii/S0370157320304269. 
  6. ↑ 6.0 6.1 6.2 6.3 6.4 6.5 6.6 Parviainen, Robert (2005). Connectivity Properties of Archimedean and Laves Lattices. 34. Uppsala Dissertations in Mathematics. pp. 37. ISBN 978-91-506-1751-1. http://urn.kb.se/resolve?urn=urn:nbn:se:uu:diva-4251. 
  7. ↑ 7.0 7.1 7.2 7.3 7.4 7.5 7.6 7.7 7.8 Suding, P. N.; R. M. Ziff (1999). "Site percolation thresholds for Archimedean lattices". Physical Review E 60 (1): 275–283. doi:10.1103/PhysRevE.60.275. PMID 11969760. Bibcode: 1999PhRvE..60..275S. 
  8. ↑ 8.0 8.1 8.2 8.3 8.4 8.5 8.6 Parviainen, Robert (2007). "Estimation of bond percolation thresholds on the Archimedean lattices". Journal of Physics A 40 (31): 9253–9258. doi:10.1088/1751-8113/40/31/005. Bibcode: 2007JPhA...40.9253P. 
  9. ↑ 9.0 9.1 9.2 9.3 9.4 9.5 9.6 9.7 9.8 Ding, Chengxiang; Zhe Fu. Wenan Guo; F. Y. Wu (2010). "Critical frontier for the Potts and percolation models on triangular-type and kagome-type lattices II: Numerical analysis". Physical Review E 81 (6): 061111. doi:10.1103/PhysRevE.81.061111. PMID 20866382. Bibcode: 2010PhRvE..81f1111D. 
  10. ↑ 10.0 10.1 Scullard, C. R.; J. L. Jacobsen (2012). "Transfer matrix computation of generalised critical polynomials in percolation". arXiv:1209.1451 [cond-mat.stat-mech].
  11. ↑ 11.00 11.01 11.02 11.03 11.04 11.05 11.06 11.07 11.08 11.09 11.10 11.11 11.12 11.13 11.14 11.15 11.16 11.17 11.18 11.19 11.20 11.21 Jacobsen, J. L. (2014). "High-precision percolation thresholds and Potts-model critical manifolds from graph polynomials". Journal of Physics A 47 (13): 135001. doi:10.1088/1751-8113/47/13/135001. Bibcode: 2014JPhA...47m5001G. 
  12. ↑ 12.0 12.1 Jacobsen, Jesper L.; Christian R. Scullard (2013). "Critical manifolds, graph polynomials, and exact solvability". StatPhys 25, Seoul, Korea July 21–26. http://www.statphys25.org/data/Statphys25%20Abstract%20Book.pdf. 
  13. ↑ 13.0 13.1 13.2 13.3 13.4 13.5 13.6 13.7 Scullard, Christian R.; Jesper Lykke Jacobsen (2020). "Bond percolation thresholds on Archimedean lattices from critical polynomial roots". Physical Review Research 2 (1): 012050. doi:10.1103/PhysRevResearch.2.012050. Bibcode: 2020PhRvR...2a2050S. 
  14. ↑ 14.0 14.1 14.2 14.3 14.4 d'Iribarne, C.; Rasigni, M.; Rasigni, G. (1995). "Determination of site percolation transitions for 2D mosaics by means of the minimal spanning tree approach". Physics Letters A 209 (1–2): 95–98. doi:10.1016/0375-9601(95)00794-8. Bibcode: 1995PhLA..209...95D. 
  15. ↑ 15.0 15.1 15.2 15.3 15.4 15.5 15.6 15.7 15.8 15.9 d'Iribarne, C.; Rasigni, M.; Rasigni, G. (1999). "From lattice long-range percolation to the continuum one". Phys. Lett. A 263 (1–2): 65–69. doi:10.1016/S0375-9601(99)00585-X. Bibcode: 1999PhLA..263...65D. 
  16. ↑ 16.0 16.1 Schliecker, G.; C. Kaiser (1999). "Percolation on disordered mosaics". Physica A 269 (2–4): 189–200. doi:10.1016/S0378-4371(99)00093-X. Bibcode: 1999PhyA..269..189S. 
  17. ↑ Djordjevic, Z. V.; H. E. Stanley; Alla Margolina (1982). "Site percolation threshold for honeycomb and square lattices". Journal of Physics A 15 (8): L405–L412. doi:10.1088/0305-4470/15/8/006. Bibcode: 1982JPhA...15L.405D. 
  18. ↑ 18.0 18.1 18.2 18.3 18.4 Feng, Xiaomei; Youjin Deng; H. W. J. Blöte (2008). "Percolation transitions in two dimensions". Physical Review E 78 (3): 031136. doi:10.1103/PhysRevE.78.031136. PMID 18851022. Bibcode: 2008PhRvE..78c1136F. http://resolver.tudelft.nl/uuid:68f9f8de-e483-4bce-b1a9-828eb52ee99b. 
  19. ↑ 19.0 19.1 19.2 19.3 19.4 19.5 19.6 Ziff, R. M.; Hang Gu (2008). "Universal condition for critical percolation thresholds of kagomé-like lattices". Physical Review E 79 (2): 020102. doi:10.1103/PhysRevE.79.020102. PMID 19391694. 
  20. ↑ 20.0 20.1 20.2 20.3 20.4 Sykes, M. F.; J. W. Essam (1964). "Exact critical percolation probabilities for site and bond problems in two dimensions". Journal of Mathematical Physics 5 (8): 1117–1127. doi:10.1063/1.1704215. Bibcode: 1964JMP.....5.1117S. 
  21. ↑ Ziff, R. M.; P. W. Suding (1997). "Determination of the bond percolation threshold for the kagome lattice". Journal of Physics A 30 (15): 5351–5359. doi:10.1088/0305-4470/30/15/021. Bibcode: 1997JPhA...30.5351Z. 
  22. ↑ Scullard, C. R. (2012). "Percolation critical polynomial as a graph invariant". Physical Review E 86 (4): 1131. doi:10.1103/PhysRevE.86.041131. PMID 23214553. Bibcode: 2012PhRvE..86d1131S. 
  23. ↑ 23.0 23.1 Jacobsen, J. L. (2015). "Critical points of Potts and O(N) models from eigenvalue identities in periodic Temperley-Lieb algebras". Journal of Physics A 48 (45): 454003. doi:10.1088/1751-8113/48/45/454003. Bibcode: 2015JPhA...48S4003L. 
  24. ↑ Lin, Keh Ying; Wen Jong Ma (1983). "Two-dimensional Ising model on a ruby lattice". Journal of Physics A 16 (16): 3895–3898. doi:10.1088/0305-4470/16/16/027. Bibcode: 1983JPhA...16.3895L. 
  25. ↑ Derrida, B.; D. Stauffer (1985). "Corrections to scaling and phenomenological renormalization for 2-dimensional percolation and lattice animal problems". Journal de Physique 46 (45): 1623. doi:10.1051/jphys:0198500460100162300. https://hal.archives-ouvertes.fr/jpa-00210110/file/ajp-jphys_1985_46_10_1623_0.pdf. 
  26. ↑ Yang, Y.; S. Zhou.; Y. Li. (2013). "Square++: Making a connection game win-lose complementary and playing-fair". Entertainment Computing 4 (2): 105–113. doi:10.1016/j.entcom.2012.10.004. 
  27. ↑ Newman, M. E. J.; R. M. Ziff (2000). "Efficient Monte-Carlo algorithm and high-precision results for percolation". Physical Review Letters 85 (19): 4104–7. doi:10.1103/PhysRevLett.85.4104. PMID 11056635. Bibcode: 2000PhRvL..85.4104N. 
  28. ↑ Mertens, Stephan (2022). "Exact site-percolation probability on the square lattice". Journal of Physics A: Mathematical and Theoretical 55 (33): 334002. doi:10.1088/1751-8121/ac4195. ISSN 1751-8113. Bibcode: 2022JPhA...55G4002M. https://iopscience.iop.org/article/10.1088/1751-8121/ac4195. 
  29. ↑ de Oliveira, P.M.C.; R. A. Nobrega; D. Stauffer (2003). "Corrections to finite size scaling in percolation". Brazilian Journal of Physics 33 (3): 616–618. doi:10.1590/S0103-97332003000300025. Bibcode: 2003BrJPh..33..616O. 
  30. ↑ Lee, M. J. (2007). "Complementary algorithms for graphs and percolation". Physical Review E 76 (2): 027702. doi:10.1103/PhysRevE.76.027702. PMID 17930184. Bibcode: 2007PhRvE..76b7702L. 
  31. ↑ Lee, M. J. (2008). "Pseudo-random-number generators and the square site percolation threshold". Physical Review E 78 (3): 031131. doi:10.1103/PhysRevE.78.031131. PMID 18851017. Bibcode: 2008PhRvE..78c1131L. 
  32. ↑ Levenshteĭn, M. E.; B. I. Shklovskiĭ; M. S. Shur; A. L. Éfros (1975). "The relation between the critical exponents of percolation theory". Zh. Eksp. Teor. Fiz. 69: 386–392. Bibcode: 1975JETP...42..197L. 
  33. ↑ Dean, P.; N. F. Bird (1967). "Monte Carlo estimates of critical percolation probabilities". Proc. Camb. Phil. Soc. 63 (2): 477–479. doi:10.1017/s0305004100041438. Bibcode: 1967PCPS...63..477D. 
  34. ↑ Dean, P (1963). "A new Monte Carlo method for percolation problems on a lattice". Proc. Camb. Phil. Soc. 59 (2): 397–410. doi:10.1017/s0305004100037026. Bibcode: 1963PCPS...59..397D. 
  35. ↑ Tencer, John; Forsberg, Kelsey Meeks (2021). "Postprocessing techniques for gradient percolation predictions on the square lattice". Phys. Rev. E 103 (1): 012115. doi:10.1103/PhysRevE.103.012115. PMID 33601521. Bibcode: 2021PhRvE.103a2115T. 
  36. ↑ Betts, D. D. (1995). "A new two-dimensional lattice of coordination number five". Proc. Nova Scotian Inst. Sci. 40: 95–100. http://hdl.handle.net/10222/35332. 
  37. ↑ 37.0 37.1 d'Iribarne, C.; Rasigni, M.; Rasigni, G. (1999). "Minimal spanning tree and percolation on mosaics: graph theory and percolation". J. Phys. A: Math. Gen. 32 (14): 2611–2622. doi:10.1088/0305-4470/32/14/002. Bibcode: 1999JPhA...32.2611D. 
  38. ↑ 38.00 38.01 38.02 38.03 38.04 38.05 38.06 38.07 38.08 38.09 38.10 38.11 38.12 38.13 38.14 38.15 38.16 38.17 38.18 38.19 38.20 38.21 38.22 van der Marck, Steven C. (1997). "Percolation thresholds and universal formulas". Physical Review E 55 (2): 1514–1517. doi:10.1103/PhysRevE.55.1514. Bibcode: 1997PhRvE..55.1514V. 
  39. ↑ 39.0 39.1 39.2 39.3 39.4 39.5 Malarz, K.; S. Galam (2005). "Square-lattice site percolation at increasing ranges of neighbor bonds". Physical Review E 71 (1): 016125. doi:10.1103/PhysRevE.71.016125. PMID 15697676. Bibcode: 2005PhRvE..71a6125M. 
  40. ↑ 40.00 40.01 40.02 40.03 40.04 40.05 40.06 40.07 40.08 40.09 40.10 40.11 40.12 40.13 40.14 40.15 40.16 40.17 40.18 40.19 40.20 40.21 40.22 40.23 40.24 40.25 40.26 Majewski, M.; K. Malarz (2007). "Square lattice site percolation thresholds for complex neighbourhoods". Acta Phys. Pol. B 38 (38): 2191. Bibcode: 2007AcPPB..38.2191M. 
  41. ↑ 41.0 41.1 41.2 41.3 41.4 41.5 41.6 41.7 41.8 41.9 Dalton, N. W.; C. Domb; M. F. Sykes (1964). "Dependence of critical concentration of a dilute ferromagnet on the range of interaction". Proc. Phys. Soc. 83 (3): 496–498. doi:10.1088/0370-1328/83/3/118. 
  42. ↑ Collier, Andrew. "Percolation Threshold: Including Next-Nearest Neighbours". http://www.exegetic.biz/blog/2013/11/percolation-threshold-including-next-nearest-neighbours/. 
  43. ↑ 43.00 43.01 43.02 43.03 43.04 43.05 43.06 43.07 43.08 43.09 43.10 43.11 43.12 43.13 Ouyang, Yunqing; Y. Deng; Henk W. J. Blöte (2018). "Equivalent-neighbor percolation models in two dimensions: Crossover between mean-field and short-range behavior". Phys. Rev. E 98 (6): 062101. doi:10.1103/PhysRevE.98.062101. Bibcode: 2018PhRvE..98f2101O. 
  44. ↑ 44.0 44.1 Xu, Wenhui; Junfeng Wang; Hao Hu; Youjin Deng (2021). "Critical polynomials in the nonplanar and continuum percolation models". Physical Review E 103 (2): 022127. doi:10.1103/PhysRevE.103.022127. ISSN 2470-0045. PMID 33736116. Bibcode: 2021PhRvE.103b2127X. 
  45. ↑ 45.00 45.01 45.02 45.03 45.04 45.05 45.06 45.07 45.08 45.09 45.10 45.11 45.12 45.13 45.14 45.15 45.16 45.17 45.18 45.19 45.20 45.21 45.22 45.23 45.24 45.25 Xun, Zhipeng; DaPeng Hao; Robert M. Ziff (2022). "Site and bond percolation thresholds on regular lattices with compact extended-range neighborhoods in two and three dimensions". Phys. Rev. E 105 (2): 024105. doi:10.1103/PhysRevE.105.024105. PMID 35291074. Bibcode: 2022PhRvE.105b4105X. 
  46. ↑ 46.0 46.1 46.2 46.3 46.4 46.5 46.6 Malarz, Krzysztop (2021). "Percolation thresholds on a triangular lattice for neighborhoods containing sites up to the fifth coordination zone". Physical Review E 103 (5): 052107. doi:10.1103/PhysRevE.103.052107. PMID 34134312. Bibcode: 2021PhRvE.103e2107M. 
  47. ↑ 47.0 47.1 47.2 47.3 47.4 47.5 47.6 Malarz, Krzysztof (2020). "Site percolation thresholds on triangular lattice with complex neighborhoods". Chaos: An Interdisciplinary Journal of Nonlinear Science 30 (12): 123123. doi:10.1063/5.0022336. PMID 33380057. Bibcode: 2020Chaos..30l3123M. 
  48. ↑ 48.0 48.1 48.2 48.3 48.4 48.5 Domb, C.; N. W. Dalton (1966). "Crystal statistics with long-range forces I. The equivalent neighbour model". Proc. Phys. Soc. 89 (4): 859–871. doi:10.1088/0370-1328/89/4/311. Bibcode: 1966PPS....89..859D. 
  49. ↑ 49.0 49.1 49.2 49.3 49.4 Gouker, Mark; Family, Fereydoon (1983). "Evidence for classical critical behavior in long-range site percolation". Phys. Rev. B 28 (3): 1449. doi:10.1103/PhysRevB.28.1449. Bibcode: 1983PhRvB..28.1449G. 
  50. ↑ Malarz, Krzysztof (2022). "Random site percolation on honeycomb lattices with complex neighborhoods". Chaos: An Interdisciplinary Journal of Nonlinear Science 32 (8): 083123. doi:10.1063/5.0099066. PMID 36049902. 
  51. ↑ 51.00 51.01 51.02 51.03 51.04 51.05 51.06 51.07 51.08 51.09 51.10 51.11 51.12 51.13 51.14 51.15 51.16 51.17 51.18 51.19 51.20 51.21 51.22 51.23 51.24 51.25 51.26 51.27 51.28 51.29 51.30 51.31 51.32 51.33 51.34 51.35 51.36 51.37 51.38 51.39 51.40 51.41 51.42 Mecke, K. R.; Seyfried, A (2002). "Strong dependence of percolation thresholds on polydispersity". Europhysics Letters (EPL) 58 (1): 28–34. doi:10.1209/epl/i2002-00601-y. Bibcode: 2002EL.....58...28M. 
  52. ↑ 52.00 52.01 52.02 52.03 52.04 52.05 52.06 52.07 52.08 52.09 52.10 52.11 52.12 52.13 52.14 52.15 52.16 52.17 52.18 52.19 52.20 52.21 52.22 Koza, Zbigniew; Kondrat, Grzegorz; Suszczyński, Karol (2014). "Percolation of overlapping squares or cubes on a lattice". Journal of Statistical Mechanics: Theory and Experiment 2014 (11): P11005. doi:10.1088/1742-5468/2014/11/P11005. Bibcode: 2014JSMTE..11..005K. 
  53. ↑ 53.0 53.1 53.2 Deng, Youjin; Yunqing Ouyang; Henk W. J. Blöte (2019). "Medium-range percolation in two dimensions". J. Phys.: Conf. Ser. 1163 (1): 012001. doi:10.1088/1742-6596/1163/1/012001. Bibcode: 2019JPhCS1163a2001D. 
  54. ↑ 54.0 54.1 54.2 Mitra, S.; D. Saha; A. Sensharma (2019). "Percolation in a distorted square lattice". Phys. Rev. E 99 (1): 012117. doi:10.1103/PhysRevE.99.012117. PMID 30780325. Bibcode: 2019PhRvE..99a2117M. 
  55. ↑ 55.0 55.1 55.2 55.3 55.4 55.5 Jasna, C. K.; V. Sasidevan (2023). "Effect of shape asymmetry on percolation of aligned and overlapping objects on lattices". Preprint. 
  56. ↑ 56.0 56.1 56.2 56.3 Scullard, C. R.; R. M. Ziff (2010). "Critical surfaces for general inhomogeneous bond percolation problems". Journal of Statistical Mechanics: Theory and Experiment 2010 (3): P03021. doi:10.1088/1742-5468/2010/03/P03021. Bibcode: 2010JSMTE..03..021S. 
  57. ↑ 57.0 57.1 Wu, F. Y. (1979). "Critical point of planar Potts models". Journal of Physics C 12 (17): L645–L650. doi:10.1088/0022-3719/12/17/002. Bibcode: 1979JPhC...12L.645W. 
  58. ↑ 58.0 58.1 Mai, T. (1980). Sinha, S. K.. ed. Ordering in two dimensions. North-Holland, Amsterdam. pp. 369-371. 
  59. ↑ 59.0 59.1 59.2 59.3 59.4 59.5 59.6 59.7 59.8 59.9 Kundu, Sumanta; Manna, S. S. (2017-05-15). "Colored percolation" (in en). Physical Review E 95 (5). doi:10.1103/PhysRevE.95.052124. ISSN 2470-0045. http://link.aps.org/doi/10.1103/PhysRevE.95.052124. 
  60. ↑ Nakanishi, H (1987). "Critical behaviour of AB percolation in two dimensions". Journal of Physics A: Mathematical and General 20 (17): 6075–6083. doi:10.1088/0305-4470/20/17/040. ISSN 0305-4470. https://iopscience.iop.org/article/10.1088/0305-4470/20/17/040. 
  61. ↑ Debierre, J -M; Bradley, R M (1992). "Scaling properties of antipercolation hulls on the triangular lattice". Journal of Physics A: Mathematical and General 25 (2): 335–343. doi:10.1088/0305-4470/25/2/014. ISSN 0305-4470. https://iopscience.iop.org/article/10.1088/0305-4470/25/2/014. 
  62. ↑ Wu, Xian-Yuan; Popov, S. Yu. (2003). "On AB Bond Percolation on the Square Lattice and AB Site Percolation on Its Line Graph". Journal of Statistical Physics 110 (1/2): 443–449. doi:10.1023/A:1021091316925. http://link.springer.com/10.1023/A:1021091316925. 
  63. ↑ 63.0 63.1 63.2 63.3 63.4 63.5 63.6 Hovi, J.-P.; A. Aharony (1996). "Scaling and universality in the spanning probability for percolation". Physical Review E 53 (1): 235–253. doi:10.1103/PhysRevE.53.235. PMID 9964253. Bibcode: 1996PhRvE..53..235H. 
  64. ↑ 64.00 64.01 64.02 64.03 64.04 64.05 64.06 64.07 64.08 64.09 64.10 64.11 64.12 64.13 64.14 64.15 64.16 64.17 64.18 Tarasevich, Yuriy Yu; Steven C. van der Marck (1999). "An investigation of site-bond percolation on many lattices". Int. J. Mod. Phys. C 10 (7): 1193–1204. doi:10.1142/S0129183199000978. Bibcode: 1999IJMPC..10.1193T. 
  65. ↑ 65.0 65.1 65.2 65.3 65.4 65.5 65.6 65.7 65.8 65.9 González-Flores, M. I.; A. A. Torres; W. Lebrecht; A. J. Ramirez-Pastor (2021). "Site-bond percolation in two-dimensional kagome lattices: Analytical approach and numerical simulations". Phys. Rev. E 104 (1): 014130. doi:10.1103/PhysRevE.104.014130. PMID 34412224. Bibcode: 2021PhRvE.104a4130G. 
  66. ↑ 66.0 66.1 66.2 66.3 66.4 Sakamoto, S.; F. Yonezawa; M. Hori (1989). "A proposal for the estimation of percolation thresholds in two-dimensional lattices". J. Phys. A 22 (14): L699–L704. doi:10.1088/0305-4470/22/14/009. Bibcode: 1989JPhA...22L.699S. 
  67. ↑ Deng, Y.; Y. Huang; J. L. Jacobsen; J. Salas; A. D. Sokal (2011). "Finite-temperature phase transition in a class of four-state Potts antiferromagnets". Physical Review Letters 107 (15): 150601. doi:10.1103/PhysRevLett.107.150601. PMID 22107278. Bibcode: 2011PhRvL.107o0601D. 
  68. ↑ Syozi, I (1972). "Transformation of Ising Models". in Domb, C.; Green, M. S.. Phase Transitions in Critical Phenomena. 1. Academic Press, London. pp. 270–329. 
  69. ↑ 69.00 69.01 69.02 69.03 69.04 69.05 69.06 69.07 69.08 69.09 69.10 69.11 69.12 69.13 69.14 69.15 69.16 69.17 69.18 69.19 69.20 Neher, Richard; Mecke, Klaus; Wagner, Herbert (2008). "Topological estimation of percolation thresholds". Journal of Statistical Mechanics: Theory and Experiment 2008 (1): P01011. doi:10.1088/1742-5468/2008/01/P01011. Bibcode: 2008JSMTE..01..011N. 
  70. ↑ Grimmett, G.; Manolescu, I (2012). "Bond percolation on isoradial graphs: Criticality and universality". Probability Theory and Related Fields 159 (1–2): 273–327. doi:10.1007/s00440-013-0507-y. 
  71. ↑ 71.0 71.1 Scullard, C. R. (2006). "Exact site percolation thresholds using a site-to-bond transformation and the star-triangle transformation". Physical Review E 73 (1): 016107. doi:10.1103/PhysRevE.73.016107. PMID 16486216. Bibcode: 2006PhRvE..73a6107S. 
  72. ↑ 72.0 72.1 72.2 72.3 Ziff, R. M. (2006). "Generalized cell–dual-cell transformation and exact thresholds for percolation". Physical Review E 73 (1): 016134. doi:10.1103/PhysRevE.73.016134. PMID 16486243. Bibcode: 2006PhRvE..73a6134Z. 
  73. ↑ 73.00 73.01 73.02 73.03 73.04 73.05 73.06 73.07 73.08 73.09 73.10 73.11 73.12 Scullard, C. R.; Robert M Ziff (2006). "Exact bond percolation thresholds in two dimensions". Journal of Physics A 39 (49): 15083–15090. doi:10.1088/0305-4470/39/49/003. Bibcode: 2006JPhA...3915083Z. 
  74. ↑ Ding, Chengxiang; Yancheng Wang; Yang Li (2012). "Potts and percolation models on bowtie lattices". Physical Review E 86 (2): 021125. doi:10.1103/PhysRevE.86.021125. PMID 23005740. Bibcode: 2012PhRvE..86b1125D. 
  75. ↑ Wierman, John (1984). "A bond percolation critical probability determination based on the star-triangle transformation". J. Phys. A: Math. Gen. 17 (7): 1525–1530. doi:10.1088/0305-4470/17/7/020. Bibcode: 1984JPhA...17.1525W. 
  76. ↑ Mahmood Maher al-Naqsh (1983). "MAH 007". The Design and Execution of Drawings in Iranian Tilework. http://patterninislamicart.com/drawings-diagrams-analyses/9/design-execution-drawings-iranian-tilework/mah007. 
  77. ↑ "Western tomb tower, Kharraqan". http://www.tilingsearch.org/HTML/data181/V1P138.html. 
  78. ↑ 78.00 78.01 78.02 78.03 78.04 78.05 78.06 78.07 78.08 78.09 78.10 78.11 78.12 78.13 Melchert, Oliver; Helmut G. Katzgraber; Mark A. Novotny (2016). "Site and bond percolation thresholds in Kn,n-based lattices: Vulnerability of quantum annealers to random qubit and coupler failures on Chimera topologies". Physical Review E 93 (4): 042128. doi:10.1103/PhysRevE.93.042128. PMID 27176275. Bibcode: 2016PhRvE..93d2128M. 
  79. ↑ Okubo, S.; M. Hayashi; S. Kimura; H. Ohta; M. Motokawa; H. Kikuchi; H. Nagasawa (1998). "Submillimeter wave ESR of triangular-kagome antiferromagnet Cu9X2(cpa)6 (X=Cl, Br)". Physica B 246–247 (2): 553–556. doi:10.1016/S0921-4526(97)00985-X. Bibcode: 1998PhyB..246..553O. 
  80. ↑ 80.00 80.01 80.02 80.03 80.04 80.05 80.06 80.07 80.08 80.09 80.10 Haji Akbari, Amir; R. M. Ziff (2009). "Percolation in networks with voids and bottlenecks". Physical Review E 79 (2): 021118. doi:10.1103/PhysRevE.79.021118. PMID 19391717. Bibcode: 2009PhRvE..79b1118H. 
  81. ↑ 81.0 81.1 Cornette, V.; A. J. Ramirez-Pastor; F. Nieto (2003). "Dependence of the percolation threshold on the size of the percolating species". Physica A 327 (1): 71–75. doi:10.1016/S0378-4371(03)00453-9. Bibcode: 2003PhyA..327...71C. 
  82. ↑ 82.0 82.1 82.2 Lebrecht, W.; P. M. Centres; A. J. Ramirez-Pastor (2019). "Analytical approximation of the site percolation thresholds for monomers and dimers on two-dimensional lattices". Physica A 516: 133–143. doi:10.1016/j.physa.2018.10.023. Bibcode: 2019PhyA..516..133L. 
  83. ↑ 83.0 83.1 83.2 83.3 83.4 83.5 83.6 83.7 83.8 Longone, Pablo; P.M. Centres; A. J. Ramirez-Pastor (2019). "Percolation of aligned rigid rods on two-dimensional triangular lattices". Physical Review E 100 (5): 052104. doi:10.1103/PhysRevE.100.052104. PMID 31870027. Bibcode: 2019PhRvE.100e2104L. 
  84. ↑ 84.0 84.1 84.2 84.3 Budinski-Petkovic, Lj; I. Loncarevic; Z. M. Jacsik; S. B. Vrhovac (2016). "Jamming and percolation in random sequential adsorption of extended objects on a triangular lattice with quenched impurities". Journal of Statistical Mechanics: Theory and Experiment 2016 (5): 053101. doi:10.1088/1742-5468/2016/05/053101. Bibcode: 2016JSMTE..05.3101B. 
  85. ↑ 85.0 85.1 Cherkasova, V. A.; Yu. Yu. Tarasevich; N. I. Lebovka; N.V. Vygornitskii (2010). "Percolation of the aligned dimers on a square lattice". Eur. Phys. J. B 74 (2): 205–209. doi:10.1140/epjb/e2010-00089-2. Bibcode: 2010EPJB...74..205C. 
  86. ↑ 86.0 86.1 86.2 86.3 Leroyer, Y.; E. Pommiers (1994). "Monte Carlo analysis of percolation of line segments on a square lattice". Phys. Rev. B 50 (5): 2795–2799. doi:10.1103/PhysRevB.50.2795. PMID 9976520. Bibcode: 1994PhRvB..50.2795L. 
  87. ↑ 87.0 87.1 87.2 87.3 87.4 87.5 87.6 Vanderwalle, N.; S. Galam; M. Kramer (2000). "A new universality for random sequential deposition of needles". Eur. Phys. J. B 14 (3): 407–410. doi:10.1007/s100510051047. Bibcode: 2000EPJB...14..407V. 
  88. ↑ Kondrat, Grzegorz; Andrzej Pękalski (2001). "Percolation and jamming in random sequential adsorption of linear segments on a square lattice". Phys. Rev. E 63 (5): 051108. doi:10.1103/PhysRevE.63.051108. PMID 11414888. Bibcode: 2001PhRvE..63e1108K. 
  89. ↑ 89.0 89.1 89.2 89.3 89.4 89.5 89.6 Haji-Akbari, A.; Nasim Haji-Akbari; Robert M. Ziff (2015). "Dimer Covering and Percolation Frustration". Phys. Rev. E 92 (3): 032134. doi:10.1103/PhysRevE.92.032134. PMID 26465453. Bibcode: 2015PhRvE..92c2134H. 
  90. ↑ Zia, R. K. P. (2009). "Percolation of a collection of finite random walks: a model for gas permeation through thin polymeric membranes". Journal of Mathematical Chemistry 45: 58–64. doi:10.1007/s10910-008-9367-6. 
  91. ↑ 91.0 91.1 91.2 91.3 Wu, Yong (2008). "Two-dimensional polymer networks near percolation". Journal of Physics A 41 (2): 025008. doi:10.1088/1751-8113/41/2/025004. Bibcode: 2008JPhA...41b5004W. 
  92. ↑ 92.00 92.01 92.02 92.03 92.04 92.05 92.06 92.07 92.08 92.09 92.10 92.11 92.12 92.13 92.14 92.15 92.16 92.17 92.18 92.19 92.20 92.21 92.22 92.23 92.24 92.25 92.26 92.27 92.28 92.29 Cornette, V.; A.J. Ramirez-Pastor; F. Nieto (2003). "Percolation of polyatomic species on a square lattice". European Physical Journal B 36 (3): 391–399. doi:10.1140/epjb/e2003-00358-1. Bibcode: 2003EPJB...36..391C. 
  93. ↑ 93.0 93.1 93.2 Ziff, R. M.; C. R. Scullard; J. C. Wierman; M. R. A. Sedlock (2012). "The critical manifolds of inhomogeneous bond percolation on bow-tie and checkerboard lattices". Journal of Physics A 45 (49): 494005. doi:10.1088/1751-8113/45/49/494005. Bibcode: 2012JPhA...45W4005Z. 
  94. ↑ 94.00 94.01 94.02 94.03 94.04 94.05 94.06 94.07 94.08 94.09 94.10 Mertens, Stephan; Cristopher Moore (2012). "Continuum percolation thresholds in two dimensions". Physical Review E 86 (6): 061109. doi:10.1103/PhysRevE.86.061109. PMID 23367895. Bibcode: 2012PhRvE..86f1109M. 
  95. ↑ 95.0 95.1 95.2 95.3 Quintanilla, John A.; R. M. Ziff (2007). "Asymmetry in the percolation thresholds of fully penetrable disks with two different radii". Physical Review E 76 (5): 051115 [6 pages]. doi:10.1103/PhysRevE.76.051115. PMID 18233631. Bibcode: 2007PhRvE..76e1115Q. 
  96. ↑ 96.0 96.1 96.2 Quintanilla, J; S. Torquato; R. M. Ziff (2000). "Efficient measurement of the percolation threshold for fully penetrable discs". J. Phys. A: Math. Gen. 33 (42): L399–L407. doi:10.1088/0305-4470/33/42/104. Bibcode: 2000JPhA...33L.399Q. 
  97. ↑ Lorenz, B; I. Orgzall; H.-O. Heuer (1993). "Universality and cluster structures in continuum models of percolation with two different radius distributions". J. Phys. A: Math. Gen. 26 (18): 4711–4712. doi:10.1088/0305-4470/26/18/032. Bibcode: 1993JPhA...26.4711L. 
  98. ↑ Rosso, M (1989). "Concentration gradient approach to continuum percolation in two dimensions". J. Phys. A: Math. Gen. 22 (4): L131–L136. doi:10.1088/0305-4470/22/4/004. Bibcode: 1989JPhA...22L.131R. 
  99. ↑ 99.0 99.1 Gawlinski, Edward T; H. Eugene Stanley (1981). "Continuum percolation in two dimensions: Monte Carlo tests of scaling and universality for non-interacting discs". J. Phys. A: Math. Gen. 14 (8): L291–L299. doi:10.1088/0305-4470/14/8/007. Bibcode: 1981JPhA...14L.291G. 
  100. ↑ 100.00 100.01 100.02 100.03 100.04 100.05 100.06 100.07 100.08 100.09 100.10 100.11 100.12 100.13 100.14 100.15 100.16 100.17 Yi, Y.-B.; A. M. Sastry (2004). "Analytical approximation of the percolation threshold for overlapping ellipsoids of revolution". Proceedings of the Royal Society A 460 (5): 2353–2380. doi:10.1098/rspa.2004.1279. Bibcode: 2004RSPSA.460.2353Y. 
  101. ↑ 101.0 101.1 101.2 Pike, G. E.; C. H. Seager (1974). "Percolation and conductivity: A computer study I". Phys. Rev. B 10 (4): 1421–1434. doi:10.1103/PhysRevB.10.1421. Bibcode: 1974PhRvB..10.1421P. 
  102. ↑ 102.00 102.01 102.02 102.03 102.04 102.05 102.06 102.07 102.08 102.09 102.10 Lin, Jianjun; Chen, Huisu (2019). "Measurement of continuum percolation properties of two-dimensional particulate systems comprising congruent and binary superellipses". Powder Technology 347: 17–26. doi:10.1016/j.powtec.2019.02.036. 
  103. ↑ Li, Mingqi; Chen, Huisu; Lin, Jianjun; Zhang, Rongling; Liu, Lin (July 2021). "Effects of the pore shape polydispersity on the percolation threshold and diffusivity of porous composites: Theoretical and numerical studies". Powder Technology 386: 382–393. doi:10.1016/j.powtec.2021.03.055. ISSN 0032-5910. http://dx.doi.org/10.1016/j.powtec.2021.03.055. 
  104. ↑ Koza, Zbigniew; Piotr Brzeski; Grzegorz Kondrat (2023). "Percolation of fully penetrable disks using the three-leg cluster method". J. Phys. A: Math. Theor. (in press) (16): 165001. doi:10.1088/1751-8121/acc3d0. Bibcode: 2023JPhA...56p5001K. 
  105. ↑ 105.0 105.1 105.2 105.3 105.4 105.5 105.6 105.7 Charbonneau, Benoit; Patrick Charbonneau; Yi Hu; Zhen Yang (2021). "High-dimensional percolation criticality and hints of mean-field-like caging of the random Lorentz gas". Phys. Rev. E 104 (2): 024137. doi:10.1103/PhysRevE.104.024137. PMID 34525662. Bibcode: 2021PhRvE.104b4137C. 
  106. ↑ Gilbert, E. N. (1961). "Random Plane Networks". J. Soc. Indust. Appl. Math. 9 (4): 533–543. doi:10.1137/0109045. 
  107. ↑ Xu, Wenhui; Junfeng Wang; Hao Hu; Youjin Deng (2021). "Critical polynomials in the nonplanar and continuum percolation models". Physical Review E 103 (2): 022127. doi:10.1103/PhysRevE.103.022127. ISSN 2470-0045. PMID 33736116. Bibcode: 2021PhRvE.103b2127X. 
  108. ↑ 108.0 108.1 108.2 Tarasevich, Yuri Yu.; Andrei V. Eserkepov (2020). "Percolation thresholds for discorectangles: numerical estimation for a range of aspect ratios". Physical Review E 101 (2): 022108. doi:10.1103/PhysRevE.101.022108. PMID 32168641. Bibcode: 2020PhRvE.101b2108T. 
  109. ↑ 109.00 109.01 109.02 109.03 109.04 109.05 109.06 109.07 109.08 109.09 109.10 109.11 109.12 109.13 109.14 109.15 109.16 109.17 109.18 Li, Jiantong; Mikael Östling (2016). "Precise percolation thresholds of two-dimensional random systems comprising overlapping ellipses". Physica A 462: 940–950. doi:10.1016/j.physa.2016.06.020. Bibcode: 2016PhyA..462..940L. http://kth.diva-portal.org/smash/get/diva2:1034150/FULLTEXT01. 
  110. ↑ Nguyen, Van Lien; Enrique Canessa (1999). "Finite-size scaling in two-dimensional continuum percolation models". Modern Physics Letters B 13 (17): 577–583. doi:10.1142/S0217984999000737. Bibcode: 1999MPLB...13..577N. 
  111. ↑ Roberts, F. D. K. (1967). "A Monte Carlo Solution of a Two-Dimensional Unstructured Cluster Problem". Biometrika 54 (3/4): 625–628. doi:10.2307/2335053. PMID 6064024. 
  112. ↑ 112.00 112.01 112.02 112.03 112.04 112.05 112.06 112.07 112.08 112.09 112.10 112.11 112.12 112.13 112.14 112.15 112.16 112.17 112.18 112.19 112.20 Xia, W.; M. F. Thorpe (1988). "Percolation properties of random ellipses". Physical Review A 38 (5): 2650–2656. doi:10.1103/PhysRevA.38.2650. PMID 9900674. Bibcode: 1988PhRvA..38.2650X. 
  113. ↑ 113.00 113.01 113.02 113.03 113.04 113.05 113.06 113.07 113.08 113.09 113.10 113.11 113.12 113.13 113.14 113.15 113.16 113.17 113.18 113.19 113.20 113.21 113.22 113.23 113.24 113.25 Torquato, S.; Y. Jiao (2012). "Effect of dimensionality on the continuum percolation of overlapping hyperspheres and hypercubes. II. Simulation results and analyses". J. Chem. Phys. 137 (7): 074106. doi:10.1063/1.4742750. PMID 22920102. Bibcode: 2012JChPh.137g4106T. 
  114. ↑ 114.00 114.01 114.02 114.03 114.04 114.05 114.06 114.07 114.08 114.09 114.10 114.11 Baker, Don R.; Gerald Paul; Sameet Sreenivasan; H. Eugene Stanley (2002). "Continuum percolation threshold for interpenetrating squares and cubes". Physical Review E 66 (4): 046136 [5 pages]. doi:10.1103/PhysRevE.66.046136. PMID 12443288. Bibcode: 2002PhRvE..66d6136B. 
  115. ↑ 115.00 115.01 115.02 115.03 115.04 115.05 115.06 115.07 115.08 115.09 115.10 115.11 115.12 115.13 115.14 Li, Jiantong; Mikael Östling (2013). "Percolation thresholds of two-dimensional continuum systems of rectangles". Physical Review E 88 (1): 012101. doi:10.1103/PhysRevE.88.012101. PMID 23944408. Bibcode: 2013PhRvE..88a2101L. https://semanticscholar.org/paper/900c43839323029fb14ace3440cc2cb01fc61e06. 
  116. ↑ Li, Jiantong; Shi-Li Zhang (2009). "Finite-size scaling in stick percolation". Physical Review E 80 (4): 040104(R). doi:10.1103/PhysRevE.80.040104. PMID 19905260. Bibcode: 2009PhRvE..80d0104L. 
  117. ↑ 117.0 117.1 117.2 Tarasevich, Yuri Yu.; Andrei V. Eserkepov (2018). "Percolation of sticks: Effect of stick alignment and length dispersity". Physical Review E 98 (6): 062142. doi:10.1103/PhysRevE.98.062142. Bibcode: 2018PhRvE..98f2142T. 
  118. ↑ 118.0 118.1 118.2 118.3 118.4 118.5 118.6 118.7 118.8 Sasidevan, V. (2013). "Continuum percolation of overlapping discs with a distribution of radii having a power-law tail". Physical Review E 88 (2): 022140. doi:10.1103/PhysRevE.88.022140. PMID 24032808. Bibcode: 2013PhRvE..88b2140S. 
  119. ↑ 119.0 119.1 van der Marck, Steven C. (1996). "Network approach to void percolation in a pack of unequal spheres". Physical Review Letters 77 (9): 1785–1788. doi:10.1103/PhysRevLett.77.1785. PMID 10063171. Bibcode: 1996PhRvL..77.1785V. 
  120. ↑ 120.0 120.1 120.2 120.3 120.4 120.5 120.6 Jin, Yuliang; Patrick Charbonneau (2014). "Mapping the arrest of the random Lorentz gas onto the dynamical transition of a simple glass former". Physical Review E 91 (4): 042313. doi:10.1103/PhysRevE.91.042313. PMID 25974497. Bibcode: 2015PhRvE..91d2313J. 
  121. ↑ 121.0 121.1 Lin, Jianjun; Zhang, Wulong; Chen, Huisu; Zhang, Rongling; Liu, Lin (2019). "Effect of pore characteristic on the percolation threshold and diffusivity of porous media comprising overlapping concave-shaped pores". International Journal of Heat and Mass Transfer 138: 1333–1345. doi:10.1016/j.ijheatmasstransfer.2019.04.110. 
  122. ↑ Meeks, Kelsey; J. Tencer; M.L. Pantoya (2017). "Percolation of binary disk systems: Modeling and theory". Phys. Rev. E 95 (1): 012118. doi:10.1103/PhysRevE.95.012118. PMID 28208494. Bibcode: 2017PhRvE..95a2118M. 
  123. ↑ Quintanilla, John A. (2001). "Measurement of the percolation threshold for fully penetrable disks of different radii". Phys. Rev. E 63 (6): 061108. doi:10.1103/PhysRevE.63.061108. PMID 11415069. Bibcode: 2001PhRvE..63f1108Q. 
  124. ↑ 124.0 124.1 124.2 Melchert, Oliver (2013). "Percolation thresholds on planar Euclidean relative-neighborhood graphs". Physical Review E 87 (4): 042106. doi:10.1103/PhysRevE.87.042106. PMID 23679372. Bibcode: 2013PhRvE..87d2106M. 
  125. ↑ 125.0 125.1 Bernardi, Olivier; Curien, Nicolas; Miermont, Grėgory (2019). "A Boltzmann approach to percolation on random triangulations". Canadian Journal of Mathematics 71: 1–43. doi:10.4153/CJM-2018-009-x. 
  126. ↑ 126.0 126.1 126.2 126.3 126.4 Becker, A.; R. M. Ziff (2009). "Percolation thresholds on two-dimensional Voronoi networks and Delaunay triangulations". Physical Review E 80 (4): 041101. doi:10.1103/PhysRevE.80.041101. PMID 19905267. Bibcode: 2009PhRvE..80d1101B. 
  127. ↑ Shante, K. S.; S. Kirkpatrick (1971). "An introduction to percolation theory". Advances in Physics 20 (85): 325–357. doi:10.1080/00018737100101261. Bibcode: 1971AdPhy..20..325S. 
  128. ↑ 128.0 128.1 128.2 Hsu, H. P.; M. C. Huang (1999). "Percolation thresholds, critical exponents, and scaling functions on planar random lattices and their duals". Physical Review E 60 (6): 6361–6370. doi:10.1103/PhysRevE.60.6361. PMID 11970550. Bibcode: 1999PhRvE..60.6361H. 
  129. ↑ 129.0 129.1 Huang, Ming-Chang; Hsiao-Ping Hsu (2002). "Percolation thresholds, critical exponents, and scaling functions on spherical random lattices". International Journal of Modern Physics C 13 (3): 383–395. doi:10.1142/S012918310200319X. 
  130. ↑ 130.0 130.1 Norrenbrock, C. (2014). "Percolation threshold on planar Euclidean Gabriel Graphs". Journal of Physics A 40 (31): 9253–9258. doi:10.1088/1751-8113/40/31/005. Bibcode: 2007JPhA...40.9253P. 
  131. ↑ 131.0 131.1 Bertin, E; J.-M. Billiot; R. Drouilhet (2002). "Continuum percolation in the Gabriel graph". Adv. Appl. Probab. 34 (4): 689. doi:10.1239/aap/1037990948. 
  132. ↑ Lepage, Thibaut; Lucie Delaby; Fausto Malvagi; Alain Mazzolo (2011). "Monte Carlo simulation of fully Markovian stochastic geometries". Progress in Nuclear Science and Technology 2: 743–748. doi:10.15669/pnst.2.743. 
  133. ↑ Zhang, C.; K. De'Bell (1993). "Reformulation of the percolation problem on a quasilattice: Estimates of the percolation threshold, chemical dimension, and amplitude ratio". Phys. Rev. B 47 (14): 8558–8564. doi:10.1103/PhysRevB.47.8558. PMID 10004894. Bibcode: 1993PhRvB..47.8558Z. 
  134. ↑ Ziff, R. M.; F. Babalievski (1999). "Site percolation on the Penrose rhomb lattice". Physica A 269 (2–4): 201–210. doi:10.1016/S0378-4371(99)00166-1. Bibcode: 1999PhyA..269..201Z. 
  135. ↑ Lu, Jian Ping; Joseph L. Birman (1987). "Percolation and Scaling on a Quasilattice". Journal of Statistical Physics 46 (5/6): 1057–1066. doi:10.1007/BF01011156. Bibcode: 1987JSP....46.1057L. 
  136. ↑ 136.0 136.1 136.2 136.3 136.4 136.5 136.6 136.7 Babalievski, F. (1995). "Percolation thresholds and percolation conductivities of octagonal and dodecagonal quasicrystalline lattices". Physica A 220 (1995): 245–250. doi:10.1016/0378-4371(95)00260-E. Bibcode: 1995PhyA..220..245B. 
  137. ↑ Bollobás, Béla; Oliver Riordan (2006). "The critical probability for random Voronoi percolation in the plane is 1/2". Probab. Theory Relat. Fields 136 (3): 417–468. doi:10.1007/s00440-005-0490-z. 
  138. ↑ Angel, Omer; Schramm, Oded (2003). "Uniform infinite planar triangulation". Commun. Math. Phys. 241 (2–3): 191–213. doi:10.1007/s00220-003-0932-3. Bibcode: 2003CMaPh.241..191A. 
  139. ↑ Angel, O.; Curien, Nicolas (2014). "Percolations on random maps I: Half-plane models". Annales de l'Institut Henri Poincaré, Probabilités et Statistiques 51 (2): 405–431. doi:10.1214/13-AIHP583. Bibcode: 2015AIHPB..51..405A. 
  140. ↑ 140.0 140.1 140.2 Zierenberg, Johannes; Niklas Fricke; Martin Marenz; F. P. Spitzner; Viktoria Blavatska; Wolfhard Janke (2017). "Percolation thresholds and fractal dimensions for square and cubic lattices with long-range correlated defects". Phys. Rev. E 96 (6): 062125. doi:10.1103/PhysRevE.96.062125. PMID 29347311. Bibcode: 2017PhRvE..96f2125Z. 
  141. ↑ 141.0 141.1 141.2 141.3 141.4 141.5 141.6 Sotta, P.; D. Long (2003). "The crossover from 2D to 3D percolation: Theory and numerical simulations". Eur. Phys. J. E 11 (4): 375–388. doi:10.1140/epje/i2002-10161-6. PMID 15011039. Bibcode: 2003EPJE...11..375S. 
  142. ↑ 142.00 142.01 142.02 142.03 142.04 142.05 142.06 142.07 142.08 142.09 142.10 142.11 142.12 142.13 142.14 142.15 142.16 142.17 142.18 142.19 142.20 142.21 142.22 142.23 142.24 142.25 142.26 142.27 Horton, M. K.; Moram, M. A. (2017-04-17). "Alloy composition fluctuations and percolation in semiconductor alloy quantum wells" (in en). Applied Physics Letters 110 (16): 162103. doi:10.1063/1.4980089. ISSN 0003-6951. Bibcode: 2017ApPhL.110p2103H. 
  143. ↑ 143.0 143.1 143.2 143.3 143.4 143.5 143.6 Gliozzi, F.; S. Lottini; M. Panero; A. Rago (2005). "Random percolation as a gauge theory". Nuclear Physics B 719 (3): 255–274. doi:10.1016/j.nuclphysb.2005.04.021. Bibcode: 2005NuPhB.719..255G. 
  144. ↑ 144.0 144.1 144.2 144.3 144.4 144.5 144.6 144.7 Yoo, Ted Y.; Jonathan Tran; Shane P. Stahlheber; Carina E. Kaainoa; Kevin Djepang; Alexander R. Small (2014). "Site percolation on lattices with low average coordination numbers". Journal of Statistical Mechanics: Theory and Experiment 2014 (6): P06014. doi:10.1088/1742-5468/2014/06/p06014. Bibcode: 2014JSMTE..06..014Y. 
  145. ↑ 145.00 145.01 145.02 145.03 145.04 145.05 145.06 145.07 145.08 145.09 145.10 Tran, Jonathan; Ted Yoo; Shane Stahlheber; Alex Small (2013). "Percolation thresholds on 3-dimensional lattices with 3 nearest neighbors". Journal of Statistical Mechanics: Theory and Experiment 2013 (5): P05014. doi:10.1088/1742-5468/2013/05/P05014. Bibcode: 2013JSMTE..05..014T. 
  146. ↑ Wells, A. F. (1984). "Structures Based on the 3-Connected Net 103 – b". Journal of Solid State Chemistry 54 (3): 378–388. doi:10.1016/0022-4596(84)90169-5. Bibcode: 1984JSSCh..54..378W. 
  147. ↑ 147.0 147.1 Pant, Mihir; Don Towsley; Dirk Englund; Saikat Guha (2017). "Percolation thresholds for photonic quantum computing". Nature Communications 10 (1): 1070. doi:10.1038/s41467-019-08948-x. PMID 30842425. 
  148. ↑ Hyde, Stephen T.; O'Keeffe, Michael; Proserpio, Davide M. (2008). "A short history of an elusive yet ubiquitous structure in chemistry, materials, and mathematics". Angew. Chem. Int. Ed. 47 (42): 7996–8000. doi:10.1002/anie.200801519. PMID 18767088. 
  149. ↑ 149.0 149.1 149.2 149.3 149.4 149.5 149.6 149.7 149.8 149.9 van der Marck, Steven C. (1997). "Percolation thresholds of the duals of the face-centered-cubic, hexagonal-close-packed, and diamond lattices". Phys. Rev. E 55 (6): 6593–6597. doi:10.1103/PhysRevE.55.6593. Bibcode: 1997PhRvE..55.6593V. 
  150. ↑ 150.0 150.1 Frisch, H. L.; E. Sonnenblick; V. A. Vyssotsky; J. M. Hammersley (1961). "Critical Percolation Probabilities (Site Problem)". Physical Review 124 (4): 1021–1022. doi:10.1103/PhysRev.124.1021. Bibcode: 1961PhRv..124.1021F. 
  151. ↑ 151.0 151.1 Vyssotsky, V. A.; S. B. Gordon; H. L. Frisch; J. M. Hammersley (1961). "Critical Percolation Probabilities (Bond Problem)". Physical Review 123 (5): 1566–1567. doi:10.1103/PhysRev.123.1566. Bibcode: 1961PhRv..123.1566V. 
  152. ↑ 152.0 152.1 152.2 152.3 152.4 152.5 152.6 Gaunt, D. S.; M. F. Sykes (1983). "Series study of random percolation in three dimensions". J. Phys. A 16 (4): 783. doi:10.1088/0305-4470/16/4/016. Bibcode: 1983JPhA...16..783G. 
  153. ↑ 153.0 153.1 153.2 153.3 Xu, Xiao; Junfeng Wang; Jian-Ping Lv; Youjin Deng (2014). "Simultaneous analysis of three-dimensional percolation models". Frontiers of Physics 9 (1): 113–119. doi:10.1007/s11467-013-0403-z. Bibcode: 2014FrPhy...9..113X. 
  154. ↑ Silverman, Amihal (1990). "Site-percolation threshold for a diamond lattice with diatomic substitution". Physical Review B 42 (2): 1369–1373. doi:10.1103/PhysRevB.42.1369. PMID 9995550. Bibcode: 1990PhRvB..42.1369S. 
  155. ↑ 155.0 155.1 van der Marck, Steven C. (1997). "Erratum: Percolation thresholds and universal formulas [Phys. Rev. E 55, 1514 (1997)]". Phys. Rev. E 56 (3): 3732. doi:10.1103/PhysRevE.56.3732.2. Bibcode: 1997PhRvE..56.3732V. 
  156. ↑ 156.00 156.01 156.02 156.03 156.04 156.05 156.06 156.07 156.08 156.09 156.10 156.11 156.12 156.13 156.14 156.15 156.16 156.17 156.18 156.19 van der Marck, Steven C. (1998). "Calculation of Percolation Thresholds in High Dimensions for FCC, BCC and Diamond Lattices". International Journal of Modern Physics C 9 (4): 529–540. doi:10.1142/S0129183198000431. Bibcode: 1998IJMPC...9..529V. 
  157. ↑ 157.0 157.1 Sykes, M. F.; D. S. Gaunt; M. Glen (1976). "Percolation processes in three dimensions". J. Phys. A: Math. Gen. 9 (10): 1705–1712. doi:10.1088/0305-4470/9/10/021. Bibcode: 1976JPhA....9.1705S. 
  158. ↑ 158.0 158.1 158.2 158.3 158.4 158.5 158.6 158.7 Sykes, M. F.; J. W. Essam (1964). "Critical percolation probabilities by series method". Physical Review 133 (1A): A310–A315. doi:10.1103/PhysRev.133.A310. Bibcode: 1964PhRv..133..310S. 
  159. ↑ 159.0 159.1 159.2 159.3 159.4 159.5 van der Marck, Steven C. (1998). "Site percolation and random walks on d-dimensional Kagome lattices". Journal of Physics A 31 (15): 3449–3460. doi:10.1088/0305-4470/31/15/010. Bibcode: 1998JPhA...31.3449V. 
  160. ↑ Sur, Amit; Joel L. Lebowitz; J. Marro; M. H. Kalos; S. Kirkpatrick (1976). "Monte Carlo studies of percolation phenomena for a simple cubic lattice". Journal of Statistical Physics 15 (5): 345–353. doi:10.1007/BF01020338. Bibcode: 1976JSP....15..345S. 
  161. ↑ 161.0 161.1 Wang, J; Z. Zhou; W. Zhang; T. Garoni; Y. Deng (2013). "Bond and site percolation in three dimensions". Physical Review E 87 (5): 052107. doi:10.1103/PhysRevE.87.052107. PMID 23767487. Bibcode: 2013PhRvE..87e2107W. 
  162. ↑ Grassberger, P. (1992). "Numerical studies of critical percolation in three dimensions". J. Phys. A 25 (22): 5867–5888. doi:10.1088/0305-4470/25/22/015. Bibcode: 1992JPhA...25.5867G. 
  163. ↑ Acharyya, M.; D. Stauffer (1998). "Effects of Boundary Conditions on the Critical Spanning Probability". Int. J. Mod. Phys. C 9 (4): 643–647. doi:10.1142/S0129183198000534. Bibcode: 1998IJMPC...9..643A. 
  164. ↑ Jan, N.; D. Stauffer (1998). "Random Site Percolation in Three Dimensions". Int. J. Mod. Phys. C 9 (4): 341–347. doi:10.1142/S0129183198000261. Bibcode: 1998IJMPC...9..341J. 
  165. ↑ Deng, Youjin; H. W. J. Blöte (2005). "Monte Carlo study of the site-percolation model in two and three dimensions". Physical Review E 72 (1): 016126. doi:10.1103/PhysRevE.72.016126. PMID 16090055. Bibcode: 2005PhRvE..72a6126D. http://resolver.tudelft.nl/uuid:e987a69f-6dde-4d8d-a616-bfcde4d5bdac. 
  166. ↑ Ballesteros, P. N.; L. A. Fernández; V. Martín-Mayor; A. Muñoz Sudepe; G. Parisi; J. J. Ruiz-Lorenzo (1999). "Scaling corrections: site percolation and Ising model in three dimensions". Journal of Physics A 32 (1): 1–13. doi:10.1088/0305-4470/32/1/004. Bibcode: 1999JPhA...32....1B. 
  167. ↑ 167.0 167.1 167.2 Lorenz, C. D.; R. M. Ziff (1998). "Universality of the excess number of clusters and the crossing probability function in three-dimensional percolation". Journal of Physics A 31 (40): 8147–8157. doi:10.1088/0305-4470/31/40/009. Bibcode: 1998JPhA...31.8147L. 
  168. ↑ 168.00 168.01 168.02 168.03 168.04 168.05 168.06 168.07 168.08 168.09 168.10 Koza, Zbigniew; Jakub Poła (2016). "From discrete to continuous percolation in dimensions 3 to 7". Journal of Statistical Mechanics: Theory and Experiment 2016 (10): 103206. doi:10.1088/1742-5468/2016/10/103206. Bibcode: 2016JSMTE..10.3206K. 
  169. ↑ Škvor, Jiří; Ivo Nezbeda (2009). "Percolation threshold parameters of fluids". Physical Review E 79 (4): 041141. doi:10.1103/PhysRevE.79.041141. PMID 19518207. Bibcode: 2009PhRvE..79d1141S. 
  170. ↑ 170.0 170.1 170.2 170.3 Adler, Joan; Yigal Meir; Amnon Aharony; A. B. Harris; Lior Klein (1990). "Low-Concentration Series in General Dimension". Journal of Statistical Physics 58 (3/4): 511–538. doi:10.1007/BF01112760. Bibcode: 1990JSP....58..511A. 
  171. ↑ 171.0 171.1 171.2 171.3 171.4 171.5 171.6 171.7 Dammer, Stephan M; Haye Hinrichsen (2004). "Spreading with immunization in high dimensions". Journal of Statistical Mechanics: Theory and Experiment 2004 (7): P07011. doi:10.1088/1742-5468/2004/07/P07011. Bibcode: 2004JSMTE..07..011D. 
  172. ↑ 172.0 172.1 172.2 Lorenz, C. D.; R. M. Ziff (1998). "Precise determination of the bond percolation thresholds and finite-size scaling corrections for the sc, fcc, and bcc lattices". Physical Review E 57 (1): 230–236. doi:10.1103/PhysRevE.57.230. Bibcode: 1998PhRvE..57..230L. 
  173. ↑ 173.0 173.1 Schrenk, K. J.; N. A. M. Araújo; H. J. Herrmann (2013). "Stacked triangular lattice: percolation properties". Physical Review E 87 (3): 032123. doi:10.1103/PhysRevE.87.032123. Bibcode: 2013PhRvE..87c2123S. 
  174. ↑ Martins, P.; J. Plascak (2003). "Percolation on two- and three-dimensional lattices". Physical Review 67 (4): 046119. doi:10.1103/physreve.67.046119. PMID 12786448. Bibcode: 2003PhRvE..67d6119M. 
  175. ↑ Bradley, R. M.; P. N. Strenski; J.-M. Debierre (1991). "Surfaces of percolation clusters in three dimensions". Physical Review B 44 (1): 76–84. doi:10.1103/PhysRevB.44.76. PMID 9998221. Bibcode: 1991PhRvB..44...76B. 
  176. ↑ 176.0 176.1 176.2 176.3 176.4 176.5 Kurzawski, Ł.; K. Malarz (2012). "Simple cubic random-site percolation thresholds for complex neighbourhoods". Rep. Math. Phys. 70 (2): 163–169. doi:10.1016/S0034-4877(12)60036-6. Bibcode: 2012RpMP...70..163K. 
  177. ↑ Gallyamov, S. R.; S.A. Melchukov (2013). "Percolation threshold of a simple cubic lattice with fourth neighbors: the theory and numerical calculation with parallelization". Third International Conference "High Performance Computing" HPC-UA 2013 (Ukraine, Kyiv, October 7–11, 2013). http://hpc-ua.org/hpc-ua-13/files/proceedings/24.pdf. Retrieved August 23, 2019. 
  178. ↑ Sykes, M. F.; D. S. Gaunt; J. W. Essam (1976). "The percolation probability for the site problem on the face-centred cubic lattice". Journal of Physics A 9 (5): L43–L46. doi:10.1088/0305-4470/9/5/002. Bibcode: 1976JPhA....9L..43S. 
  179. ↑ 179.00 179.01 179.02 179.03 179.04 179.05 179.06 179.07 179.08 179.09 179.10 179.11 179.12 179.13 179.14 179.15 179.16 179.17 179.18 179.19 179.20 179.21 179.22 179.23 179.24 179.25 179.26 179.27 179.28 179.29 179.30 179.31 179.32 179.33 Hu, Yi; Patrick Charbonneau (2021). "Percolation thresholds on high-dimensional Dn and E8-related lattices". Physical Review E 103 (6): 062115. doi:10.1103/PhysRevE.103.062115. PMID 34271715. Bibcode: 2021PhRvE.103f2115H. 
  180. ↑ 180.0 180.1 Lorenz, C. D.; R. May; R. M. Ziff (2000). "Similarity of Percolation Thresholds on the HCP and FCC Lattices". Journal of Statistical Physics 98 (3/4): 961–970. doi:10.1023/A:1018648130343. https://deepblue.lib.umich.edu/bitstream/2027.42/45178/1/10955_2004_Article_222436.pdf. 
  181. ↑ Tahir-Kheli, Jamil; W. A. Goddard III (2007). "Chiral plaquette polaron theory of cuprate superconductivity". Physical Review B 76 (1): 014514. doi:10.1103/PhysRevB.76.014514. Bibcode: 2007PhRvB..76a4514T. 
  182. ↑ 182.0 182.1 182.2 182.3 182.4 182.5 182.6 Malarz, Krzysztof (2015). "Simple cubic random-site percolation thresholds for neighborhoods containing fourth-nearest neighbors". Phys. Rev. E 91 (4): 043301. doi:10.1103/PhysRevE.91.043301. PMID 25974606. Bibcode: 2015PhRvE..91d3301M. 
  183. ↑ Xun, Zhipeng; Dapeng Hao; Robert M. Ziff (2021). "Site percolation on square and simple cubic lattices with extended neighborhoods and their continuum limit". Phys. Rev. E 103 (2): 022126. doi:10.1103/PhysRevE.103.022126. PMID 33735955. Bibcode: 2021PhRvE.103b2126X. 
  184. ↑ 184.0 184.1 184.2 184.3 184.4 184.5 184.6 184.7 184.8 184.9 Xun, Zhipeng; Robert M. Ziff (2020). "Bond percolation on simple cubic lattices with extended neighborhoods". Phys. Rev. E 102 (4): 012102. doi:10.1103/PhysRevE.102.012102. PMID 32795057. Bibcode: 2020PhRvE.102a2102X. 
  185. ↑ 185.0 185.1 185.2 185.3 Jerauld, G. R.; L. E. Scriven; H. T. Davis (1984). "Percolation and conduction on the 3D Voronoi and regular networks: a second case study in topological disorder". J. Phys. C: Solid State Phys. 17 (19): 3429–3439. doi:10.1088/0022-3719/17/19/017. Bibcode: 1984JPhC...17.3429J. 
  186. ↑ Xu, Fangbo; Zhiping Xu; Boris I. Yakobson (2014). "Site-Percolation Threshold of Carbon Nanotube Fibers---Fast Inspection of Percolation with Markov Stochastic Theory". Physica A 407: 341–349. doi:10.1016/j.physa.2014.04.013. Bibcode: 2014PhyA..407..341X. 
  187. ↑ 187.0 187.1 187.2 Gawron, T. R.; Marek Cieplak (1991). "Site percolation thresholds of the FCC lattice". Acta Physica Polonica A 80 (3): 461. doi:10.12693/APhysPolA.80.461. Bibcode: 1991AcPPA..80..461G. http://przyrbwn.icm.edu.pl/APP/PDF/80/a080z3p38.pdf. 
  188. ↑ Harter, T. (2005). "Finite-size scaling analysis of percolation in three-dimensional correlated binary Markov chain random fields". Physical Review E 72 (2): 026120. doi:10.1103/PhysRevE.72.026120. PMID 16196657. Bibcode: 2005PhRvE..72b6120H. 
  189. ↑ Sykes, M. F.; J. J. Rehr; Maureen Glen (1996). "A note on the percolation probabilities of pairs of closely similar lattices". Proc. Camb. Phil. Soc. 76: 389–392. doi:10.1017/S0305004100049021. 
  190. ↑ Weber, H.; W. Paul (1996). "Penetrant diffusion in frozen polymer matrices: A finite-size scaling study of free volume percolation". Physical Review E 54 (4): 3999–4007. doi:10.1103/PhysRevE.54.3999. PMID 9965547. Bibcode: 1996PhRvE..54.3999W. 
  191. ↑ 191.0 191.1 191.2 191.3 191.4 Mitra, S.; D. Saha; A. Sensharma (2022). "Percolation in a simple cubic lattice with distortion". Phys. Rev. E 106 (3): 034109. doi:10.1103/PhysRevE.106.034109. PMID 36266842. Bibcode: 2022PhRvE.106c4109M. 
  192. ↑ Tarasevich, Yu. Yu.; V. A. Cherkasova (2007). "Dimer percolation and jamming on simple cubic lattice". European Physical Journal B 60 (1): 97–100. doi:10.1140/epjb/e2007-00321-2. Bibcode: 2007EPJB...60...97T. 
  193. ↑ Holcomb, D F..; J. J. Rehr, Jr. (1969). "Percolation in heavily doped semiconductors*". Physical Review 183 (3): 773–776. doi:10.1103/PhysRev.183.773. Bibcode: 1969PhRv..183..773H. 
  194. ↑ Holcomb, D F.; F. Holcomb; M. Iwasawa (1972). "Clustering of randomly placed spheres". Biometrika 59: 207–209. doi:10.1093/biomet/59.1.207. 
  195. ↑ Shante, Vinod K. S.; Scott Kirkpatrick (1971). "An introduction to percolation theory". Advances in Physics 20 (85): 325–357. doi:10.1080/00018737100101261. Bibcode: 1971AdPhy..20..325S. 
  196. ↑ 196.0 196.1 Rintoul, M. D.; S. Torquato (1997). "Precise determination of the critical threshold and exponents in a three-dimensional continuum percolation model". J. Phys. A: Math. Gen. 30 (16): L585. doi:10.1088/0305-4470/30/16/005. Bibcode: 1997JPhA...30L.585R. 
  197. ↑ Consiglio, R.; R. Baker; G. Paul; H. E. Stanley (2003). "Continuum percolation of congruent overlapping spherocylinders". Physica A 319: 49–55. doi:10.1016/S0378-4371(02)01501-7. 
  198. ↑ 198.0 198.1 198.2 198.3 198.4 198.5 198.6 198.7 Xu, Wenxiang; Xianglong Su; Yang Jiao (2016). "Continuum percolation of congruent overlapping spherocylinders". Phys. Rev. E 93 (3): 032122. doi:10.1103/PhysRevE.94.032122. PMID 27078307. Bibcode: 2016PhRvE..94c2122X. 
  199. ↑ 199.0 199.1 Lorenz, C. D.; R. M. Ziff (2000). "Precise determination of the critical percolation threshold for the three dimensional Swiss cheese model using a growth algorithm". J. Chem. Phys. 114 (8): 3659. doi:10.1063/1.1338506. Bibcode: 2001JChPh.114.3659L. https://deepblue.lib.umich.edu/bitstream/2027.42/70114/2/JCPSA6-114-8-3659-1.pdf. 
  200. ↑ 200.0 200.1 200.2 200.3 200.4 200.5 200.6 200.7 200.8 Lin, Jianjun; Chen, Huisu; Xu, Wenxiang (2018). "Geometrical percolation threshold of congruent cuboidlike particles in overlapping particle systems". Physical Review E 98 (1): 012134. doi:10.1103/PhysRevE.98.012134. PMID 30110832. Bibcode: 2018PhRvE..98a2134L. 
  201. ↑ 201.00 201.01 201.02 201.03 201.04 201.05 201.06 201.07 201.08 201.09 201.10 201.11 201.12 201.13 201.14 201.15 201.16 201.17 201.18 201.19 201.20 201.21 201.22 201.23 201.24 201.25 201.26 201.27 201.28 201.29 201.30 201.31 201.32 201.33 201.34 Garboczi, E. J.; K. A. Snyder; J. F. Douglas (1995). "Geometrical percolation threshold of overlapping ellipsoids". Phys. Rev. E 52 (1): 819–827. doi:10.1103/PhysRevE.52.819. PMID 9963485. Bibcode: 1995PhRvE..52..819G. https://zenodo.org/record/1233793. 
  202. ↑ 202.0 202.1 202.2 202.3 Li, Mingqi; Chen, Huisu; Lin, Jianjun (January 2020). "Efficient measurement of the percolation threshold for random systems of congruent overlapping ovoids". Powder Technology 360: 598–607. doi:10.1016/j.powtec.2019.10.044. ISSN 0032-5910. 
  203. ↑ Li, Mingqi; Chen, Huisu; Lin, Jianjun (April 2020). "Numerical study for the percolation threshold and transport properties of porous composites comprising non-centrosymmetrical superovoidal pores". Computer Methods in Applied Mechanics and Engineering 361: 112815. doi:10.1016/j.cma.2019.112815. ISSN 0045-7825. Bibcode: 2020CMAME.361k2815L. 
  204. ↑ 204.0 204.1 204.2 204.3 204.4 204.5 Dall, Jesper; Michael Christensen (2002). "Random geometric graphs". Phys. Rev. E 66 (1): 016121. doi:10.1103/PhysRevE.66.016121. PMID 12241440. Bibcode: 2002PhRvE..66a6121D. 
  205. ↑ Gori, Giacomo; Andrea Trombettoni (2015). "Conformal invariance in three dimensional percolation". Journal of Statistical Mechanics: Theory and Experiment 2015 (7): P07014. doi:10.1088/1742-5468/2015/07/P07014. Bibcode: 2015JSMTE..07..014G. 
  206. ↑ Balberg, I.; N. Binenbaum (1984). "Percolation thresholds in the three-dimensional sticks system". Phys. Rev. Lett. 52 (17): 1465. doi:10.1103/PhysRevLett.52.1465. Bibcode: 1984PhRvL..52.1465B. 
  207. ↑ 207.0 207.1 207.2 207.3 207.4 207.5 207.6 207.7 207.8 207.9 Yi, Y.-B.; A. M. Sastry (2004). "Analytical approximation of the percolation threshold for overlapping ellipsoids of revolution". Proc. R. Soc. Lond. A 460 (2048): 2353–2380. doi:10.1098/rspa.2004.1279. Bibcode: 2004RSPSA.460.2353Y. 
  208. ↑ 208.0 208.1 208.2 Hyytiä, E.; J. Virtamo; P. Lassila; J. Ott (2012). "Continuum percolation threshold for permeable aligned cylinders and opportunistic networking". IEEE Communications Letters 16 (7): 1064–1067. doi:10.1109/LCOMM.2012.051512.120497. https://zenodo.org/record/1223952. 
  209. ↑ 209.0 209.1 209.2 209.3 209.4 Torquato, S.; Y. Jiao (2012). "Effect of Dimensionality on the Percolation Threshold of Overlapping Nonspherical Hyperparticles". Physical Review E 87 (2): 022111. doi:10.1103/PhysRevE.87.022111. PMID 23496464. Bibcode: 2013PhRvE..87b2111T. 
  210. ↑ 210.0 210.1 210.2 Yi, Y. B.; E. Tawerghi (2009). "Geometric percolation thresholds of interpenetrating plates in three-dimensional space". Physical Review E 79 (4): 041134. doi:10.1103/PhysRevE.79.041134. PMID 19518200. Bibcode: 2009PhRvE..79d1134Y. 
  211. ↑ 211.0 211.1 211.2 Powell, M. J. (1979). "Site percolation in randomly packed spheres". Physical Review B 20 (10): 4194–4198. doi:10.1103/PhysRevB.20.4194. Bibcode: 1979PhRvB..20.4194P. 
  212. ↑ 212.0 212.1 Ziff, R. M.; Salvatore Torquato (2016). "Percolation of disordered jammed sphere packings". Journal of Physics A: Mathematical and Theoretical 50 (8): 085001. doi:10.1088/1751-8121/aa5664. Bibcode: 2017JPhA...50h5001Z. 
  213. ↑ 213.0 213.1 213.2 213.3 213.4 213.5 Yi, Y. B.; K. Esmail (2012). "Computational measurement of void percolation thresholds of oblate particles and thin plate composites". J. Appl. Phys. 111 (12): 124903–124903–6. doi:10.1063/1.4730333. Bibcode: 2012JAP...111l4903Y. 
  214. ↑ Lin, Jianjun; Chen, Huisu (2018). "Continuum percolation of porous media via random packing of overlapping cube-like particles". Theoretical & Applied Mechanics Letters 8 (5): 299–303. doi:10.1016/j.taml.2018.05.007. 
  215. ↑ Lin, Jianjun; Chen, Huisu (2018). "Effect of particle morphologies on the percolation of particulate porous media: A study of superballs". Powder Technology 335: 388–400. doi:10.1016/j.powtec.2018.05.015. 
  216. ↑ 216.00 216.01 216.02 216.03 216.04 216.05 216.06 216.07 216.08 216.09 216.10 216.11 Priour, Jr., D. J.; N. J. McGuigan (2018). "Percolation through voids around randomly oriented polyhedra and axially symmetric grains". Phys. Rev. Lett. 121 (22): 225701. doi:10.1103/PhysRevLett.121.225701. PMID 30547614. Bibcode: 2018PhRvL.121v5701P. 
  217. ↑ 217.0 217.1 217.2 217.3 217.4 217.5 217.6 217.7 217.8 Novak, Igor L.; Fei Gao; Pavel Kraikivski; Boris M. Slepchenko (2011). "Diffusion amid random overlapping obstacles: Similarities, invariants, approximations". J. Chem. Phys. 134 (15): 154104. doi:10.1063/1.3578684. PMID 21513372. Bibcode: 2011JChPh.134o4104N. 
  218. ↑ 218.0 218.1 218.2 218.3 218.4 218.5 Yi, Y. B. (2006). "Void percolation and conduction of overlapping ellipsoids". Physical Review E 74 (3): 031112. doi:10.1103/PhysRevE.74.031112. PMID 17025599. Bibcode: 2006PhRvE..74c1112Y. 
  219. ↑ 219.00 219.01 219.02 219.03 219.04 219.05 219.06 219.07 219.08 219.09 219.10 219.11 219.12 219.13 Ballow, A.; P. Linton; D. J. Priour Jr. (2023). "Percolation through voids around toroidal inclusions". Physical Review E 107 (1): 014902. doi:10.1103/PhysRevE.107.014902. PMID 36797924. Bibcode: 2023PhRvE.107a4902B. 
  220. ↑ 220.0 220.1 Priour, Jr., D. J.; N. J. McGuigan (2017). "Percolation through voids around randomly oriented faceted inclusions". arXiv:1712.10241 [cond-mat.stat-mech].
  221. ↑ Kertesz, Janos (1981). "Percolation of holes between overlapping spheres: Monte Carlo calculation of the critical volume fraction". Journal de Physique Lettres 42 (17): L393– L395. doi:10.1051/jphyslet:019810042017039300. https://hal.archives-ouvertes.fr/jpa-00231955/file/ajp-jphyslet_1981_42_17_393_0.pdf. 
  222. ↑ Elam, W. T.; A. R. Kerstein; J. J. Rehr (1984). "Critical properties of the void percolation problem for spheres". Phys. Rev. Lett. 52 (7): 1516–1519. doi:10.1103/PhysRevLett.52.1516. Bibcode: 1984PhRvL..52.1516E. 
  223. ↑ Rintoul, M. D. (2000). "Precise determination of the void percolation threshold for two distributions of overlapping spheres". Physical Review E 62 (6): 68–72. doi:10.1103/PhysRevE.62.68. PMID 11088435. Bibcode: 2000PhRvE..62...68R. https://digital.library.unt.edu/ark:/67531/metadc703993/. 
  224. ↑ 224.0 224.1 Höfling, F.; T. Munk; E. Frey; T. Franosch (2008). "Critical dynamics of ballistic and Brownian particles in a heterogeneous environment". J. Chem. Phys. 128 (16): 164517. doi:10.1063/1.2901170. PMID 18447469. Bibcode: 2008JChPh.128p4517H. 
  225. ↑ Priour, Jr., D.J. (2014). "Percolation through voids around overlapping spheres: A dynamically based finite-size scaling analysis". Phys. Rev. E 89 (1): 012148. doi:10.1103/PhysRevE.89.012148. PMID 24580213. Bibcode: 2014PhRvE..89a2148P. 
  226. ↑ Clerc, J. P.; G. Giraud; S. Alexander; E. Guyon (1979). "Conductivity of a mixture of conducting and insulating grains: Dimensionality effects". Physical Review B 22 (5): 2489–2494. doi:10.1103/PhysRevB.22.2489. 
  227. ↑ C. Larmier; E. Dumonteil; F. Malvagi; A. Mazzolo; A. Zoia (2016). "Finite-size effects and percolation properties of Poisson geometries". Physical Review E 94 (1): 012130. doi:10.1103/PhysRevE.94.012130. PMID 27575099. Bibcode: 2016PhRvE..94a2130L. 
  228. ↑ 228.0 228.1 228.2 228.3 228.4 228.5 Zakalyukin, R. M.; V. A. Chizhikov (2005). "Calculations of the Percolation Thresholds of a Three-Dimensional (Icosahedral) Penrose Tiling by the Cubic Approximant Method". Crystallography Reports 50 (6): 938–948. doi:10.1134/1.2132400. Bibcode: 2005CryRp..50..938Z. 
  229. ↑ Kantor, Yacov (1986). "Three-dimensional percolation with removed lines of sites". Phys. Rev. B 33 (5): 3522–3525. doi:10.1103/PhysRevB.33.3522. PMID 9938740. Bibcode: 1986PhRvB..33.3522K. 
  230. ↑ Schrenk, K. J.; M. R. Hilário; V. Sidoravicius; N. A. M. Araújo; H. J. Herrmann; M. Thielmann; A. Teixeira (2016). "Critical Fragmentation Properties of Random Drilling: How Many Holes Need to Be Drilled to Collapse a Wooden Cube?". Phys. Rev. Lett. 116 (5): 055701. doi:10.1103/PhysRevLett.116.055701. PMID 26894717. Bibcode: 2016PhRvL.116e5701S. 
  231. ↑ Grassberger, P. (2017). "Some remarks on drilling percolation". Phys. Rev. E 95 (1): 010103. doi:10.1103/PhysRevE.95.010103. PMID 28208497. http://juser.fz-juelich.de/search?p=id:%22FZJ-2017-07804%22. 
  232. ↑ Grassberger, Peter; Marcelo R. Hilário; Vladas Sidoravicius (2017). "Percolation in Media with Columnar Disorder". J. Stat. Phys. 168 (4): 731–745. doi:10.1007/s10955-017-1826-7. Bibcode: 2017JSP...168..731G. 
  233. ↑ 233.0 233.1 Szczygieł, Bartłomiej; Kamil Kwiatkowski; Maciej Lewenstein; Gerald John Lapeyre, Jr.; Jan Wehr (2016). "Percolation thresholds for discrete-continuous models with nonuniform probabilities of bond formation". Phys. Rev. E 93 (2): 022127. doi:10.1103/PhysRevE.93.022127. PMID 26986308. Bibcode: 2016PhRvE..93b2127S. 
  234. ↑ 234.0 234.1 234.2 Kirkpatrick, Scott (1976). "Percolation phenomena in higher dimensions: Approach to the mean-field limit". Physical Review Letters 36 (2): 69–72. doi:10.1103/PhysRevLett.36.69. Bibcode: 1976PhRvL..36...69K. 
  235. ↑ 235.0 235.1 235.2 235.3 Gaunt, D. S.; Sykes, M. F.; Ruskin, Heather (1976). "Percolation processes in d-dimensions". J. Phys. A: Math. Gen. 9 (11): 1899–1911. doi:10.1088/0305-4470/9/11/015. Bibcode: 1976JPhA....9.1899G. 
  236. ↑ 236.00 236.01 236.02 236.03 236.04 236.05 236.06 236.07 236.08 236.09 236.10 236.11 236.12 236.13 236.14 236.15 236.16 236.17 236.18 236.19 Grassberger, Peter (2003). "Critical percolation in high dimensions". Physical Review E 67 (3): 4. doi:10.1103/PhysRevE.67.036101. PMID 12689126. Bibcode: 2003PhRvE..67c6101G. 
  237. ↑ 237.0 237.1 Paul, Gerald; Robert M. Ziff; H. Eugene Stanley (2001). "Percolation threshold, Fisher exponent, and shortest path exponent for four and five dimensions". Physical Review E 64 (2): 8. doi:10.1103/PhysRevE.64.026115. PMID 11497659. Bibcode: 2001PhRvE..64b6115P. 
  238. ↑ Ballesteros, H. G.; L. A. Fernández; V. Martín-Mayor; A. Muñoz Sudupe; G. Parisi; J. J. Ruiz-Lorenzo (1997). "Measures of critical exponents in the four dimensional site percolation". Phys. Lett. B 400 (3–4): 346–351. doi:10.1016/S0370-2693(97)00337-7. Bibcode: 1997PhLB..400..346B. 
  239. ↑ 239.0 239.1 239.2 239.3 239.4 239.5 239.6 Kotwica, M.; P. Gronek; K. Malarz (2019). "Efficient space virtualisation for Hoshen–Kopelman algorithm". International Journal of Modern Physics C 30 (8): 1950055–1950099. doi:10.1142/S0129183119500554. Bibcode: 2019IJMPC..3050055K. 
  240. ↑ 240.00 240.01 240.02 240.03 240.04 240.05 240.06 240.07 240.08 240.09 240.10 240.11 240.12 240.13 240.14 240.15 240.16 240.17 240.18 240.19 Mertens, Stephan; Christopher Moore (2018). "Percolation Thresholds and Fisher Exponents in Hypercubic Lattices". Phys. Rev. E 98 (2): 022120. doi:10.1103/PhysRevE.98.022120. PMID 30253462. Bibcode: 2018PhRvE..98b2120M. 
  241. ↑ 241.0 241.1 241.2 241.3 Harris, A. B.; Fisch, R. (1977). "Critical Behavior of Random Resistor Networks". Physical Review Letters 38 (15): 796–799. doi:10.1103/PhysRevLett.38.796. Bibcode: 1977PhRvL..38..796H. https://link.aps.org/doi/10.1103/PhysRevLett.38.796. 
  242. ↑ 242.0 242.1 242.2 242.3 Xun, Zhipeng (2020). "Precise bond percolation thresholds on several four-dimensional lattices". Physical Review Research 2 (1): 013067. doi:10.1103/PhysRevResearch.2.013067. Bibcode: 2020PhRvR...2a3067X. 
  243. ↑ 243.0 243.1 Gaunt, D. S.; Ruskin, Heather (1978). "Bond percolation processes in d-dimensions". J. Phys. A: Math. Gen. 11 (7): 1369. doi:10.1088/0305-4470/11/7/025. Bibcode: 1978JPhA...11.1369G. 
  244. ↑ 244.0 244.1 244.2 244.3 244.4 Adler, Joan; Yigal Meir; Amnon Aharony; A. B. Harris (1990). "Series Study of Percolation Moments in General Dimension". Physical Review B 41 (13): 9183–9206. doi:10.1103/PhysRevB.41.9183. PMID 9993262. Bibcode: 1990PhRvB..41.9183A. https://repository.upenn.edu/physics_papers/368. 
  245. ↑ Stauffer, Dietrich; Robert M. Ziff (1999). "Reexamination of Seven-Dimensional Site Percolation Thresholds". International Journal of Modern Physics C 11 (1): 205–209. doi:10.1142/S0129183100000183. Bibcode: 2000IJMPC..11..205S. 
  246. ↑ Mertens, Stephan; Moore, Christopher (2018). "Series Expansion of Critical Densities for Percolation on ℤd". J. Phys. A: Math. Theor. 51 (47): 475001. doi:10.1088/1751-8121/aae65c. 
  247. ↑ 247.00 247.01 247.02 247.03 247.04 247.05 247.06 247.07 247.08 247.09 247.10 247.11 247.12 247.13 247.14 247.15 247.16 247.17 Zhao, Pengyu; Jinhong Yan; Zhipeng Xun; Dapeng Hao; Robert M. Ziff (2022). "Site and bond percolation on four-dimensional simple hypercubic lattices with extended neighborhoods". Journal of Statistical Mechanics: Theory and Experiment 2022 (3): 033202. doi:10.1088/1742-5468/ac52a8. Bibcode: 2022JSMTE2022c3202Z. 
  248. ↑ 248.0 248.1 Schulman, L. S. (1983). "Long range percolation in one dimension" (in en). Journal of Physics A: Mathematical and General 16 (17): L639–L641. doi:10.1088/0305-4470/16/17/001. ISSN 0305-4470. Bibcode: 1983JPhA...16L.639S. 
  249. ↑ Aizenman, M.; Newman, C. M. (1986-12-01). "Discontinuity of the percolation density in one dimensional 1/|x−y|2 percolation models" (in en). Communications in Mathematical Physics 107 (4): 611–647. doi:10.1007/BF01205489. ISSN 0010-3616. Bibcode: 1986CMaPh.107..611A. 
  250. ↑ 250.0 250.1 Gori, G.; Michelangeli, M.; Defenu, N.; Trombettoni, A. (2017). "One-dimensional long-range percolation: A numerical study". Physical Review E 96 (1): 012108. doi:10.1103/physreve.96.012108. PMID 29347133. Bibcode: 2017PhRvE..96a2108G. 
  251. ↑ Baek, S.K.; Petter Minnhagen; Beom Jun Kim (2009). "Comment on 'Monte Carlo simulation study of the two-stage percolation transition in enhanced binary trees'". J. Phys. A: Math. Theor. 42 (47): 478001. doi:10.1088/1751-8113/42/47/478001. Bibcode: 2009JPhA...42U8001B. 
  252. ↑ 252.0 252.1 252.2 Boettcher, Stefan; Jessica L. Cook; Robert M. Ziff (2009). "Patchy percolation on a hierarchical network with small-world bonds". Phys. Rev. E 80 (4): 041115. doi:10.1103/PhysRevE.80.041115. PMID 19905281. Bibcode: 2009PhRvE..80d1115B. 
  253. ↑ 253.00 253.01 253.02 253.03 253.04 253.05 253.06 253.07 253.08 253.09 253.10 253.11 253.12 253.13 253.14 253.15 253.16 253.17 253.18 253.19 253.20 253.21 253.22 253.23 253.24 253.25 253.26 253.27 253.28 253.29 253.30 253.31 253.32 253.33 253.34 253.35 253.36 253.37 253.38 253.39 Mertens, Stephan; Cristopher Moore (2017). "Percolation thresholds in hyperbolic lattices". Phys. Rev. E 96 (4): 042116. doi:10.1103/PhysRevE.96.042116. PMID 29347529. Bibcode: 2017PhRvE..96d2116M. 
  254. ↑ 254.0 254.1 254.2 Lopez, Jorge H.; J. M. Schwarz (2017). "Constraint percolation on hyperbolic lattices". Phys. Rev. E 96 (5): 052108. doi:10.1103/PhysRevE.96.052108. PMID 29347694. Bibcode: 2017PhRvE..96e2108L. 
  255. ↑ 255.0 255.1 255.2 255.3 255.4 255.5 255.6 255.7 255.8 Baek, S.K.; Petter Minnhagen; Beom Jun Kim (2009). "Percolation on hyperbolic lattices". Phys. Rev. E 79 (1): 011124. doi:10.1103/PhysRevE.79.011124. PMID 19257018. Bibcode: 2009PhRvE..79a1124B. 
  256. ↑ 256.0 256.1 256.2 256.3 256.4 256.5 256.6 256.7 Gu, Hang; Robert M. Ziff (2012). "Crossing on hyperbolic lattices". Phys. Rev. E 85 (5): 051141. doi:10.1103/PhysRevE.85.051141. PMID 23004737. Bibcode: 2012PhRvE..85e1141G. 
  257. ↑ 257.0 257.1 257.2 257.3 Nogawa, Tomoaki; Takehisa Hasegawa (2009). "Monte Carlo simulation study of the two-stage percolation transition in enhanced binary trees". J. Phys. A: Math. Theor. 42 (14): 145001. doi:10.1088/1751-8113/42/14/145001. Bibcode: 2009JPhA...42n5001N. 
  258. ↑ 258.0 258.1 Minnhagen, Petter; Seung Ki Baek (2010). "Analytic results for the percolation transitions of the enhanced binary tree". Phys. Rev. E 82 (1): 011113. doi:10.1103/PhysRevE.82.011113. PMID 20866571. Bibcode: 2010PhRvE..82a1113M. 
  259. ↑ Kozáková, Iva (2009). "Critical percolation of virtually free groups and other tree-like graphs". Annals of Probability 37 (6): 2262–2296. doi:10.1214/09-AOP458. 
  260. ↑ 260.00 260.01 260.02 260.03 260.04 260.05 260.06 260.07 260.08 260.09 260.10 260.11 260.12 260.13 260.14 260.15 260.16 260.17 260.18 260.19 260.20 260.21 260.22 260.23 260.24 260.25 260.26 260.27 260.28 260.29 260.30 260.31 260.32 260.33 Wang, Junfeng; Zongzheng Zhou; Qingquan Liu; Timothy M. Garoni; Youjin Deng (2013). "A high-precision Monte Carlo study of directed percolation in (d + 1) dimensions". Physical Review E 88 (4): 042102. doi:10.1103/PhysRevE.88.042102. PMID 24229111. Bibcode: 2013PhRvE..88d2102W. 
  261. ↑ 261.0 261.1 Jensen, Iwan; Anthony J. Guttmann (1995). "Series expansions of the percolation probability for directed square and honeycomb lattices". J. Phys. A: Math. Gen. 28 (17): 4813–4833. doi:10.1088/0305-4470/28/17/015. Bibcode: 1995JPhA...28.4813J. 
  262. ↑ 262.0 262.1 Jensen, Iwan (2004). "Low-density series expansions for directed percolation: III. Some two-dimensional lattices". J. Phys. A: Math. Gen. 37 (4): 6899–6915. doi:10.1088/0305-4470/37/27/003. Bibcode: 2004JPhA...37.6899J. 
  263. ↑ 263.0 263.1 263.2 263.3 Essam, J. W.; A. J. Guttmann; K. De'Bell (1988). "On two-dimensional directed percolation". J. Phys. A 21 (19): 3815–3832. doi:10.1088/0305-4470/21/19/018. Bibcode: 1988JPhA...21.3815E. 
  264. ↑ Lübeck, S.; R. D. Willmann (2002). "Universal scaling behaviour of directed percolation and the pair contact process in an external field". J. Phys. A 35 (48): 10205. doi:10.1088/0305-4470/35/48/301. Bibcode: 2002JPhA...3510205L. 
  265. ↑ 265.0 265.1 Jensen, Iwan (1999). "Low-density series expansions for directed percolation: I. A new efficient algorithm with applications to the square lattice". J. Phys. A 32 (28): 5233–5249. doi:10.1088/0305-4470/32/28/304. Bibcode: 1999JPhA...32.5233J. 
  266. ↑ Essam, John (1986). "Analysis of extended series for bond percolation on the directed square lattice". Physical Review B 33 (2): 1982–1986. doi:10.1103/PhysRevB.33.1982. PMID 9938508. Bibcode: 1986PhRvB..33.1982E. 
  267. ↑ Baxter, R. J.; A. J. Guttmann (1988). "Series expansion of the percolation probability for the directed square lattice". J. Phys. A 21 (15): 3193–3204. doi:10.1088/0305-4470/21/15/008. Bibcode: 1988JPhA...21.3193B. 
  268. ↑ 268.0 268.1 268.2 Jensen, Iwan (1996). "Low-density series expansions for directed percolation on square and triangular lattices". J. Phys. A 29 (22): 7013–7040. doi:10.1088/0305-4470/29/22/007. Bibcode: 1996JPhA...29.7013J. 
  269. ↑ 269.0 269.1 269.2 269.3 269.4 269.5 269.6 269.7 269.8 269.9 Blease, J. (1977). "Series expansions for the directed-bond percolation problem". J. Phys. C: Solid State Phys. 10 (7): 917–924. doi:10.1088/0022-3719/10/7/003. Bibcode: 1977JPhC...10..917B. 
  270. ↑ 270.0 270.1 270.2 Grassberger, P.; Y.-C. Zhang (1996). ""Self-organized" formulation of standard percolation phenomena". Physica A 224 (1): 169–179. doi:10.1016/0378-4371(95)00321-5. Bibcode: 1996PhyA..224..169G. 
  271. ↑ 271.0 271.1 271.2 271.3 271.4 271.5 Grassberger, P. (2009). "Local persistence in directed percolation". Journal of Statistical Mechanics: Theory and Experiment 2009 (8): P08021. doi:10.1088/1742-5468/2009/08/P08021. Bibcode: 2009JSMTE..08..021G. 
  272. ↑ 272.0 272.1 272.2 272.3 Lübeck, S.; R. D. Willmann (2004). "Universal scaling behavior of directed percolation around the upper critical dimension". J. Stat. Phys. 115 (5–6): 1231–1250. doi:10.1023/B:JOSS.0000028059.24904.3b. Bibcode: 2004JSP...115.1231L. 
  273. ↑ Perlsman, E.; S. Havlin (2002). "Method to estimate critical exponents using numerical studies". Europhys. Lett. 58 (2): 176–181. doi:10.1209/epl/i2002-00621-7. Bibcode: 2002EL.....58..176P. https://semanticscholar.org/paper/502191a5395e90141d8f22da5576825a693cda5a. 
  274. ↑ Adler, Joan; J. Berger; M. A. M. S. Duarte; Y. Meir (1988). "Directed percolation in 3+1 dimensions". Physical Review B 37 (13): 7529–7533. doi:10.1103/PhysRevB.37.7529. PMID 9944046. Bibcode: 1988PhRvB..37.7529A. 
  275. ↑ 275.0 275.1 Grassberger, Peter (2009). "Logarithmic corrections in (4 + 1)-dimensional directed percolation". Physical Review E 79 (5): 052104. doi:10.1103/PhysRevE.79.052104. PMID 19518501. Bibcode: 2009PhRvE..79e2104G. 
  276. ↑ Soares, Danyel J. B.; José S Andrade Jr; Hans J. Herrmann (2006). "Precise calculation of the threshold of various directed percolation models on a square lattice". J. Phys. A: Math. Gen. 38 (21): L413–L415. doi:10.1088/0305-4470/38/21/L06. 
  277. ↑ Tretyakov, A. Yu.; N Inui (1995). "Critical behaviour for mixed site-bond directed percolation". J. Phys. A: Math. Gen. 28 (14): 3985–3990. doi:10.1088/0305-4470/28/14/017. Bibcode: 1995JPhA...28.3985T. 
  278. ↑ Wu, F. Y. (2010). "Critical frontier of the Potts and percolation models on triangular-type and kagome-type lattices I: Closed-form expressions". Physical Review E 81 (6): 061110. doi:10.1103/PhysRevE.81.061110. PMID 20866381. Bibcode: 2010PhRvE..81f1110W. 
  279. ↑ Damavandi, Ojan Khatib; Robert M. Ziff (2015). "Percolation on hypergraphs with four-edges". J. Phys. A: Math. Theor. 48 (40): 405004. doi:10.1088/1751-8113/48/40/405004. Bibcode: 2015JPhA...48N5004K. 
  280. ↑ 280.0 280.1 Wu, F. Y. (2006). "New Critical Frontiers for the Potts and Percolation Models". Physical Review Letters 96 (9): 090602. doi:10.1103/PhysRevLett.96.090602. PMID 16606250. Bibcode: 2006PhRvL..96i0602W. 



Retrieved from "https://handwiki.org/wiki/index.php?title=Percolation_threshold&oldid=3359883"