Elongated triangular tiling

In geometry, the elongated triangular tiling is a semiregular tiling of the Euclidean plane. There are three triangles and two squares on each vertex. It is named as a triangular tiling elongated by rows of squares, and given Schläfli symbol {3,6}:e.

Conway calls it a isosnub quadrille.

There are 3 regular and 8 semiregular tilings in the plane. This tiling is similar to the snub square tiling which also has 3 triangles and two squares on a vertex, but in a different order.

Construction

It is also the only convex uniform tiling that can not be created as a Wythoff construction. It can be constructed as alternate layers of apeirogonal prisms and apeirogonal antiprisms.

Uniform colorings

There is one uniform colorings of an elongated triangular tiling. Two 2-uniform colorings have a single vertex figure, 11123, with two colors of squares, but are not 1-uniform, repeated either by reflection or glide reflection, or in general each row of squares can be shifted around independently. The 2-uniform tilings are also called Archimedean colorings. There are infinite variations of these Archimedean colorings by arbitrary shifts in the square row colorings.

11122 (1-uniform)	11123 (2-uniform or 1-Archimedean)
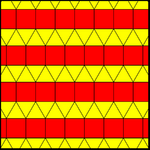
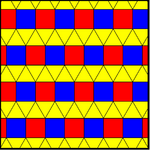
cmm (2*22)	pmg (22*)	pgg (22×)

Circle packing

The elongated triangular tiling can be used as a circle packing, placing equal diameter circles at the center of every point. Every circle is in contact with 5 other circles in the packing (kissing number).

Related tilings

Sections of stacked triangles and squares can be combined into radial forms. This mixes two vertex configurations, 3.3.3.4.4 and 3.3.4.3.4 on the transitions. Twelve copies are needed to fill the plane with different center arrangements. The duals will mix in cairo pentagonal tiling pentagons.

Example radial forms

Center	Triangle		Square		Hexagon
Symmetry	[3]	[3]+	[2]	[4]+	[6]	[6]+
Tower
Dual

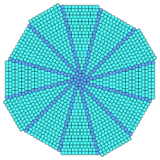
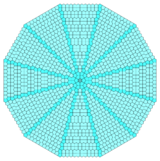
Symmetry mutations

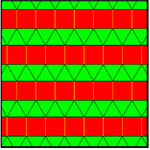
It is first in a series of symmetry mutations with hyperbolic uniform tilings with 2*n2 orbifold notation symmetry, vertex figure 4.n.4.3.3.3, and Coxeter diagram . Their duals have hexagonal faces in the hyperbolic plane, with face configuration V4.n.4.3.3.3.

Symmetry mutation 2*n2 of uniform tilings: 4.n.4.3.3.3

4.2.4.3.3.3	4.3.4.3.3.3	4.4.4.3.3.3
2*22	2*32	2*42
	or	or

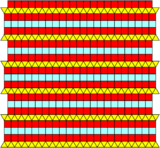
There are four related 2-uniform tilings, mixing 2 or 3 rows of triangles or squares.

Double elongated	Triple elongated	Half elongated	One third elongated

Prismatic pentagonal tiling

Prismatic pentagonal tiling
Type	Dual uniform tiling
Faces	irregular pentagons V3.3.3.4.4
Coxeter diagram
Symmetry group	cmm, [∞,2+,∞], (2*22)
Dual polyhedron	Elongated triangular tiling
Properties	face-transitive

The prismatic pentagonal tiling is a dual uniform tiling in the Euclidean plane. It is one of 15 known isohedral pentagon tilings. It can be seen as a stretched hexagonal tiling with a set of parallel bisecting lines through the hexagons.

Conway calls it an iso(4-)pentille. Each of its pentagonal faces has three 120° and two 90° angles.

It is related to the Cairo pentagonal tiling with face configuration V3.3.4.3.4.

Geometric variations

Monohedral pentagonal tiling type 6 has the same topology, but two edge lengths and a lower p2 (2222) wallpaper group symmetry:

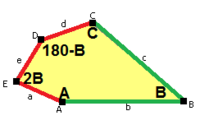a=d=e, b=c B+D=180°, 2B=E

Related 2-uniform dual tilings

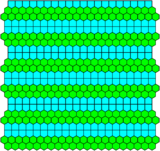
There are four related 2-uniform dual tilings, mixing in rows of squares or hexagons (the prismatic pentagon is half-square half-hexagon).

Dual: Double Elongated	Dual: Triple Elongated	Dual: Half Elongated	Dual: One-Third Elongated
Dual: [44; 33.42]1 (t=2,e=4)	Dual: [44; 33.42]2 (t=3,e=5)	Dual: [36; 33.42]1 (t=3,e=4)	Dual: [36; 33.42]2 (t=4,e=5)

See also

• Tilings of regular polygons
• Elongated triangular prismatic honeycomb
• Gyroelongated triangular prismatic honeycomb

References

• Grünbaum, Branko; Shephard, G. C. (1987). Tilings and Patterns. New York: W. H. Freeman. ISBN 0-7167-1193-1. https://archive.org/details/isbn_0716711931.  (Chapter 2.1: Regular and uniform tilings, p. 58-65)
• Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X.  p37
• John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN:978-1-56881-220-5 [1]
• Keith Critchlow, Order in Space: A design source book, 1970, p. 69-61, Pattern Q₂, Dual p. 77-76, pattern 6
• Dale Seymour and Jill Britton, Introduction to Tessellations, 1989, ISBN:978-0866514613, pp. 50–56

External links

• Weisstein, Eric W.. "Uniform tessellation". http://mathworld.wolfram.com/UniformTessellation.html. 
• Weisstein, Eric W.. "Semiregular tessellation". http://mathworld.wolfram.com/SemiregularTessellation.html. 
• Klitzing, Richard. "2D Euclidean tilings elong( x3o6o ) - etrat - O4". https://bendwavy.org/klitzing/dimensions/flat.htm#2D.