Physics:Field electron emission
Field electron emission, also known as field emission (FE) and electron field emission, is emission of electrons induced by an electrostatic field. The most common context is field emission from a solid surface into a vacuum. However, field emission can take place from solid or liquid surfaces, into a vacuum, a fluid (e.g. air), or any non-conducting or weakly conducting dielectric. The field-induced promotion of electrons from the valence to conduction band of semiconductors (the Zener effect) can also be regarded as a form of field emission. The terminology is historical because related phenomena of surface photoeffect, thermionic emission (or Richardson–Dushman effect) and "cold electronic emission", i.e. the emission of electrons in strong static (or quasi-static) electric fields, were discovered and studied independently from the 1880s to 1930s. When field emission is used without qualifiers it typically means "cold emission".
Field emission in pure metals occurs in high electric fields: the gradients are typically higher than 1 gigavolt per metre and strongly dependent upon the work function. While electron sources based on field emission have a number of applications, field emission is most commonly an undesirable primary source of vacuum breakdown and electrical discharge phenomena, which engineers work to prevent. Examples of applications for surface field emission include the construction of bright electron sources for high-resolution electron microscopes or the discharge of induced charges from spacecraft. Devices which eliminate induced charges are termed charge-neutralizers.
Field emission was explained by quantum tunneling of electrons in the late 1920s. This was one of the triumphs of the nascent quantum mechanics. The theory of field emission from bulk metals was proposed by Ralph H. Fowler and Lothar Wolfgang Nordheim.[1] A family of approximate equations, Fowler–Nordheim equations, is named after them. Strictly, Fowler–Nordheim equations apply only to field emission from bulk metals and (with suitable modification) to other bulk crystalline solids, but they are often used – as a rough approximation – to describe field emission from other materials.
Terminology and conventions
Field electron emission, field-induced electron emission, field emission and electron field emission are general names for this experimental phenomenon and its theory. The first name is used here.
Fowler–Nordheim tunneling is the wave-mechanical tunneling of electrons through a rounded triangular barrier created at the surface of an electron conductor by applying a very high electric field. Individual electrons can escape by Fowler–Nordheim tunneling from many materials in various different circumstances.
Cold field electron emission (CFE) is the name given to a particular statistical emission regime, in which the electrons in the emitter are initially in internal thermodynamic equilibrium, and in which most emitted electrons escape by Fowler–Nordheim tunneling from electron states close to the emitter Fermi level. (By contrast, in the Schottky emission regime, most electrons escape over the top of a field-reduced barrier, from states well above the Fermi level.) Many solid and liquid materials can emit electrons in a CFE regime if an electric field of an appropriate size is applied.
Fowler–Nordheim-type equations are a family of approximate equations derived to describe CFE from the internal electron states in bulk metals. The different members of the family represent different degrees of approximation to reality. Approximate equations are necessary because, for physically realistic models of the tunneling barrier, it is mathematically impossible in principle to solve the Schrödinger equation exactly in any simple way. There is no theoretical reason to believe that Fowler–Nordheim-type equations validly describe field emission from materials other than bulk crystalline solids.
For metals, the CFE regime extends to well above room temperature. There are other electron emission regimes (such as "thermal electron emission" and "Schottky emission") that require significant external heating of the emitter. There are also emission regimes where the internal electrons are not in thermodynamic equilibrium and the emission current is, partly or completely, determined by the supply of electrons to the emitting region. A non-equilibrium emission process of this kind may be called field (electron) emission if most of the electrons escape by tunneling, but strictly it is not CFE, and is not accurately described by a Fowler–Nordheim-type equation.
Care is necessary because in some contexts (e.g. spacecraft engineering), the name "field emission" is applied to the field-induced emission of ions (field ion emission), rather than electrons, and because in some theoretical contexts "field emission" is used as a general name covering both field electron emission and field ion emission.
Historically, the phenomenon of field electron emission has been known by a variety of names, including "the aeona effect", "autoelectronic emission", "cold emission", "cold cathode emission", "field emission", "field electron emission" and "electron field emission".
Equations in this article are written using the International System of Quantities (ISQ). This is the modern (post-1970s) international system, based around the rationalized-meter-kilogram-second (rmks) system of equations, which is used to define SI units. Older field emission literature (and papers that directly copy equations from old literature) often write some equations using an older equation system that does not use the quantity ε0. In this article, all such equations have been converted to modern international form. For clarity, this should always be done.
Since work function is normally given in electronvolts (eV), and it is often convenient to measure fields in volts per nanometer (V/nm), values of most universal constants are given here in units involving the eV, V and nm. Increasingly, this is normal practice in field emission research. However, all equations here are ISQ-compatible equations and remain dimensionally consistent, as is required by the modern international system. To indicate their status, numerical values of universal constants are given to seven significant figures. Values are derived using the 2006 values of the fundamental constants.
Early history of field electron emission
Field electron emission has a long, complicated and messy history. This section covers the early history, up to the derivation of the original Fowler–Nordheim-type equation in 1928.
In retrospect, it seems likely that the electrical discharges reported by J.H. Winkler[2] in 1744 were started by CFE from his wire electrode. However, meaningful investigations had to wait until after J.J. Thomson's[3] identification of the electron in 1897, and until after it was understood – from thermal emission[4] and photo-emission[5] work – that electrons could be emitted from inside metals (rather than from surface-adsorbed gas molecules), and that – in the absence of applied fields – electrons escaping from metals had to overcome a work function barrier.
It was suspected at least as early as 1913 that field-induced emission was a separate physical effect.[6] However, only after vacuum and specimen cleaning techniques had significantly improved, did this become well established. Lilienfeld (who was primarily interested in electron sources for medical X-ray applications) published in 1922[7] the first clear account in English of the experimental phenomenology of the effect he had called "autoelectronic emission". He had worked on this topic, in Leipzig, since about 1910. Kleint describes this and other early work.[8][9]
After 1922, experimental interest increased, particularly in the groups led by Millikan at the California Institute of Technology (Caltech) in Pasadena, California,[10] and by Gossling at the General Electric Company in London.[11] Attempts to understand autoelectronic emission included plotting experimental current–voltage (i–V) data in different ways, to look for a straight-line relationship. Current increased with voltage more rapidly than linearly, but plots of type log(i) vs. V were not straight.[10] Walter H. Schottky[12] suggested in 1923 that the effect might be due to thermally induced emission over a field-reduced barrier. If so, then plots of log(i) vs. √V should be straight, but they were not.[10] Nor is Schottky's explanation compatible with the experimental observation of only very weak temperature dependence in CFE[7] – a point initially overlooked.[6]
A breakthrough came when C.C. Lauritsen[13] (and J. Robert Oppenheimer independently[14]) found that plots of log(i) vs. 1/V yielded good straight lines. This result, published by Millikan and Lauritsen[13] in early 1928, was known to Fowler and Nordheim.
Oppenheimer had predicted[14] that the field-induced tunneling of electrons from atoms (the effect now called field ionization) would have this i(V) dependence, had found this dependence in the published experimental field emission results of Millikan and Eyring,[10] and proposed that CFE was due to field-induced tunneling of electrons from atomic-like orbitals in surface metal atoms. An alternative Fowler–Nordheim theory[1] explained both the Millikan–Lauritsen finding and the very weak dependence of current on temperature. Fowler–Nordheim theory predicted both to be consequences if CFE were due to field-induced tunneling from free-electron-type states in what we would now call a metal conduction band, with the electron states occupied in accordance with Fermi–Dirac statistics.
Oppenheimer had mathematical details of his theory seriously incorrect.[15] There was also a small numerical error in the final equation given by Fowler–Nordheim theory for CFE current density: this was corrected in the 1929 paper of (Stern Gossling).[16]
Strictly, if the barrier field in Fowler–Nordheim 1928 theory is exactly proportional to the applied voltage, and if the emission area is independent of voltage, then the Fowler–Nordheim 1928 theory predicts that plots of the form (log(i/V2) vs. 1/V) should be exact straight lines. However, contemporary experimental techniques were not good enough to distinguish between the Fowler–Nordheim theoretical result and the Millikan–Lauritsen experimental result.
Thus, by 1928 basic physical understanding of the origin of CFE from bulk metals had been achieved, and the original Fowler–Nordheim-type equation had been derived.
The literature often presents Fowler–Nordheim work as a proof of the existence of electron tunneling, as predicted by wave-mechanics. Whilst this is correct, the validity of wave-mechanics was largely accepted by 1928. The more important role of the Fowler–Nordheim paper was that it was a convincing argument from experiment that Fermi–Dirac statistics applied to the behavior of electrons in metals, as suggested by Sommerfeld[17] in 1927. The success of Fowler–Nordheim theory did much to support the correctness of Sommerfeld's ideas, and greatly helped to establish modern electron band theory.[18] In particular, the original Fowler–Nordheim-type equation was one of the first to incorporate the statistical-mechanical consequences of the existence of electron spin into the theory of an experimental condensed-matter effect. The Fowler–Nordheim paper also established the physical basis for a unified treatment of field-induced and thermally induced electron emission.[18] Prior to 1928 it had been hypothesized that two types of electrons, "thermions" and "conduction electrons", existed in metals, and that thermally emitted electron currents were due to the emission of thermions, but that field-emitted currents were due to the emission of conduction electrons. The Fowler–Nordheim 1928 work suggested that thermions did not need to exist as a separate class of internal electrons: electrons could come from a single band occupied in accordance with Fermi–Dirac statistics, but would be emitted in statistically different ways under different conditions of temperature and applied field.
The ideas of Oppenheimer, Fowler and Nordheim were also an important stimulus to the development, by George Gamow,[19] and Ronald W. Gurney and Edward Condon,[20][21] later in 1928, of the theory of the radioactive decay of nuclei (by alpha particle tunneling).[22]
Practical applications: past and present
Field electron microscopy and related basics
As already indicated, the early experimental work on field electron emission (1910–1920)[7] was driven by Lilienfeld's desire to develop miniaturized X-ray tubes for medical applications. However, it was too early for this technology to succeed.
After Fowler–Nordheim theoretical work in 1928, a major advance came with the development in 1937 by Erwin W. Mueller of the spherical-geometry field electron microscope (FEM)[23] (also called the "field emission microscope"). In this instrument, the electron emitter is a sharply pointed wire, of apex radius r. This is placed, in a vacuum enclosure, opposite an image detector (originally a phosphor screen), at a distance R from it. The microscope screen shows a projection image of the distribution of current-density J across the emitter apex, with magnification approximately (R/r), typically 105 to 106. In FEM studies the apex radius is typically 100 nm to 1 μm. The tip of the pointed wire, when referred to as a physical object, has been called a "field emitter", a "tip", or (recently) a "Mueller emitter".
When the emitter surface is clean, this FEM image is characteristic of: (a) the material from which the emitter is made: (b) the orientation of the material relative to the needle/wire axis; and (c) to some extent, the shape of the emitter endform. In the FEM image, dark areas correspond to regions where the local work function φ is relatively high and/or the local barrier field F is relatively low, so J is relatively low; the light areas correspond to regions where φ is relatively low and/or F is relatively high, so J is relatively high. This is as predicted by the exponent of Fowler–Nordheim-type equations [see eq. (30) below].
The adsorption of layers of gas atoms (such as oxygen) onto the emitter surface, or part of it, can create surface electric dipoles that change the local work function of this part of the surface. This affects the FEM image; also, the change of work-function can be measured using a Fowler–Nordheim plot (see below). Thus, the FEM became an early observational tool of surface science.[24][25] For example, in the 1960s, FEM results contributed significantly to discussions on heterogeneous catalysis.[26] FEM has also been used for studies of surface-atom diffusion. However, FEM has now been almost completely superseded by newer surface-science techniques.
A consequence of FEM development, and subsequent experimentation, was that it became possible to identify (from FEM image inspection) when an emitter was "clean", and hence exhibiting its clean-surface work-function as established by other techniques. This was important in experiments designed to test the validity of the standard Fowler–Nordheim-type equation.[27][28] These experiments deduced a value of voltage-to-barrier-field conversion factor β from a Fowler–Nordheim plot (see below), assuming the clean-surface φ–value for tungsten, and compared this with values derived from electron-microscope observations of emitter shape and electrostatic modeling. Agreement to within about 10% was achieved. Only very recently[29] has it been possible to do the comparison the other way round, by bringing a well-prepared probe so close to a well-prepared surface that approximate parallel-plate geometry can be assumed and the conversion factor can be taken as 1/W, where W is the measured probe-to emitter separation. Analysis of the resulting Fowler–Nordheim plot yields a work-function value close to the independently known work-function of the emitter.
Field electron spectroscopy (electron energy analysis)
Energy distribution measurements of field-emitted electrons were first reported in 1939.[30] In 1959 it was realized theoretically by Young,[31] and confirmed experimentally by Young and Mueller[32] that the quantity measured in spherical geometry was the distribution of the total energy of the emitted electron (its "total energy distribution"). This is because, in spherical geometry, the electrons move in such a fashion that angular momentum about a point in the emitter is very nearly conserved. Hence any kinetic energy that, at emission, is in a direction parallel to the emitter surface gets converted into energy associated with the radial direction of motion. So what gets measured in an energy analyzer is the total energy at emission.
With the development of sensitive electron energy analyzers in the 1960s, it became possible to measure fine details of the total energy distribution. These reflect fine details of the surface physics, and the technique of Field Electron Spectroscopy flourished for a while, before being superseded by newer surface-science techniques.[33][34]
Field electron emitters as electron-gun sources

To achieve high-resolution in electron microscopes and other electron beam instruments (such as those used for electron beam lithography), it is helpful to start with an electron source that is small, optically bright and stable. Sources based on the geometry of a Mueller emitter qualify well on the first two criteria. The first electron microscope (EM) observation of an individual atom was made by Crewe, Wall and Langmore in 1970,[35] using a scanning electron microscope equipped with an early field emission gun.
From the 1950s onwards, extensive effort has been devoted to the development of field emission sources for use in electron guns.[36][37][38] [e.g., DD53] Methods have been developed for generating on-axis beams, either by field-induced emitter build-up, or by selective deposition of a low-work-function adsorbate (usually Zirconium oxide – ZrO) into the flat apex of a (100) oriented Tungsten emitter.[39]
Sources that operate at room temperature have the disadvantage that they rapidly become covered with adsorbate molecules that arrive from the vacuum system walls, and the emitter has to be cleaned from time to time by "flashing" to high temperature. Nowadays, it is more common to use Mueller-emitter-based sources that are operated at elevated temperatures, either in the Schottky emission regime or in the so-called temperature-field intermediate regime. Many modern high-resolution electron microscopes and electron beam instruments use some form of Mueller-emitter-based electron source. Currently, attempts are being made to develop carbon nanotubes (CNTs) as electron-gun field emission sources.[40][41]
The use of field emission sources in electron optical instruments has involved the development of appropriate theories of charged particle optics,[37][42] and the development of related modeling. Various shape models have been tried for Mueller emitters; the best seems to be the "Sphere on Orthogonal Cone" (SOC) model introduced by Dyke, Trolan. Dolan and Barnes in 1953.[43] Important simulations, involving trajectory tracing using the SOC emitter model, were made by Wiesener and Everhart.[44][45][46] Nowadays, the facility to simulate field emission from Mueller emitters is often incorporated into the commercial electron-optics programmes used to design electron beam instruments. The design of efficient modern field-emission electron guns requires highly specialized expertise.
Atomically sharp emitters
Nowadays it is possible to prepare very sharp emitters, including emitters that end in a single atom. In this case, electron emission comes from an area about twice the crystallographic size of a single atom. This was demonstrated by comparing FEM and field ion microscope (FIM) images of the emitter.[47] Single-atom-apex Mueller emitters also have relevance to the scanning probe microscopy and helium scanning ion microscopy (He SIM).[48] Techniques for preparing them have been under investigation for many years.[47][49] A related important recent advance has been the development (for use in the He SIM) of an automated technique for restoring a three-atom ("trimer") apex to its original state, if the trimer breaks up.[48]
Large-area field emission sources: vacuum nanoelectronics
Materials aspects
Large-area field emission sources have been of interest since the 1970s. In these devices, a high density of individual field emission sites is created on a substrate (originally silicon). This research area became known, first as "vacuum microelectronics", now as "vacuum nanoelectronics".
One of the original two device types, the "Spindt array",[50] used silicon-integrated-circuit (IC) fabrication techniques to make regular arrays in which molybdenum cones were deposited in small cylindrical voids in an oxide film, with the void covered by a counterelectrode with a central circular aperture. This overall geometry has also been used with carbon nanotubes grown in the void.
The other original device type was the "Latham emitter".[51][52] These were MIMIV (metal-insulator-metal-insulator-vacuum) – or, more generally, CDCDV (conductor-dielectric-conductor-dielectric-vacuum) – devices that contained conducting particulates in a dielectric film. The device field-emits because its microstructure/nanostructure has field-enhancing properties. This material had a potential production advantage, in that it could be deposited as an "ink", so IC fabrication techniques were not needed. However, in practice, uniformly reliable devices proved difficult to fabricate.
Research advanced to look for other materials that could be deposited/grown as thin films with suitable field-enhancing properties. In a parallel-plate arrangement, the "macroscopic" field FM between the plates is given by FM = V/W, where W is the plate separation and V is the applied voltage. If a sharp object is created on one plate, then the local field F at its apex is greater than FM and can be related to FM by
The parameter γ is called the "field enhancement factor" and is basically determined by the object's shape. Since field emission characteristics are determined by the local field F, then the higher the γ-value of the object, then the lower the value of FM at which significant emission occurs. Hence, for a given value of W, the lower the applied voltage V at which significant emission occurs.
For a roughly ten year-period from the mid-1990s, there was great interest in field emission from plasma-deposited films of amorphous and "diamond-like" carbon.[53][54] However, interest subsequently lessened, partly due to the arrival of CNT emitters, and partly because evidence emerged that the emission sites might be associated with particulate carbon objects created in an unknown way during the deposition process: this suggested that quality control of an industrial-scale production process might be problematic.
The introduction of CNT field emitters,[41] both in "mat" form and in "grown array" forms, was a significant step forward. Extensive research has been undertaken into both their physical characteristics and possible technological applications.[40] For field emission, an advantage of CNTs is that, due to their shape, with its high aspect ratio, they are "natural field-enhancing objects".
In recent years there has also been massive growth in interest in the development of other forms of thin-film emitter, both those based on other carbon forms (such as "carbon nanowalls[55] ") and on various forms of wide-band-gap semiconductor.[56] A particular aim is to develop "high-γ" nanostructures with a sufficiently high density of individual emission sites. Thin films of nanotubes in form of nanotube webs are also used for development of field emission electrodes.[57][58][59] It is shown that by fine-tuning the fabrication parameters, these webs can achieve an optimum density of individual emission sites.[57] Double-layered electrodes made by deposition of two layers of these webs with perpendicular alignment towards each other are shown to be able to lower the turn-on electric field (electric field required for achieving an emission current of 10 μA/cm2) down to 0.3 V/μm and provide a stable field emission performance.[58]
Common problems with all field-emission devices, particularly those that operate in "industrial vacuum conditions" is that the emission performance can be degraded by the adsorption of gas atoms arriving from elsewhere in the system, and the emitter shape can be in principle be modified deleteriously by a variety of unwanted subsidiary processes, such as bombardment by ions created by the impact of emitted electrons onto gas-phase atoms and/or onto the surface of counter-electrodes. Thus, an important industrial requirement is "robustness in poor vacuum conditions"; this needs to be taken into account in research on new emitter materials.
At the time of writing, the most promising forms of large-area field emission source (certainly in terms of achieved average emission current density) seem to be Spindt arrays and the various forms of source based on CNTs.
Applications
The development of large-area field emission sources was originally driven by the wish to create new, more efficient, forms of electronic information display. These are known as "field-emission displays" or "nano-emissive displays". Although several prototypes have been demonstrated,[40] the development of such displays into reliable commercial products has been hindered by a variety of industrial production problems not directly related to the source characteristics [En08].
Other proposed applications of large-area field emission sources[40] include microwave generation, space-vehicle neutralization, X-ray generation, and (for array sources) multiple e-beam lithography. There are also recent attempts to develop large-area emitters on flexible substrates, in line with wider trends towards "plastic electronics".
The development of such applications is the mission of vacuum nanoelectronics. However, field emitters work best in conditions of good ultrahigh vacuum. Their most successful applications to date (FEM, FES and EM guns) have occurred in these conditions. The sad fact remains that field emitters and industrial vacuum conditions do not go well together, and the related problems of reliably ensuring good "vacuum robustness" of field emission sources used in such conditions still await better solutions (probably cleverer materials solutions) than we currently have.
Vacuum breakdown and electrical discharge phenomena
As already indicated, it is now thought that the earliest manifestations of field electron emission were the electrical discharges it caused. After Fowler–Nordheim work, it was understood that CFE was one of the possible primary underlying causes of vacuum breakdown and electrical discharge phenomena. (The detailed mechanisms and pathways involved can be very complicated, and there is no single universal cause)[60] Where vacuum breakdown is known to be caused by electron emission from a cathode, then the original thinking was that the mechanism was CFE from small conducting needle-like surface protrusions. Procedures were (and are) used to round and smooth the surfaces of electrodes that might generate unwanted field electron emission currents. However the work of Latham and others[51] showed that emission could also be associated with the presence of semiconducting inclusions in smooth surfaces. The physics of how the emission is generated is still not fully understood, but suspicion exists that so-called "triple-junction effects" may be involved. Further information may be found in Latham's book[51] and in the on-line bibliography.[60]
Internal electron transfer in electronic devices
In some electronic devices, electron transfer from one material to another, or (in the case of sloping bands) from one band to another ("Zener tunneling"), takes place by a field-induced tunneling process that can be regarded as a form of Fowler–Nordheim tunneling. For example, Rhoderick's book discusses the theory relevant to metal–semiconductor contacts.[61]
Fowler–Nordheim tunneling
Introduction
The next part of this article deals with the basic theory of cold field electron emission from bulk metals. This is best treated in four main stages, involving theory associated with: (1) derivation of a formula for "escape probability", by considering electron tunneling through a rounded triangular barrier; (2) an integration over internal electron states to obtain the "total energy distribution"; (3) a second integration, to obtain the emission current density as a function of local barrier field and local work function; (4) conversion of this to a formula for current as a function of applied voltage. The modified equations needed for large-area emitters, and issues of experimental data analysis, are dealt with separately.
Fowler–Nordheim tunneling is the wave-mechanical tunneling of an electron through an exact or rounded triangular barrier. Two basic situations are recognized: (1) when the electron is initially in a localized state; (2) when the electron is initially not strongly localized, and is best represented by a travelling wave. Emission from a bulk metal conduction band is a situation of the second type, and discussion here relates to this case. It is also assumed that the barrier is one-dimensional (i.e., has no lateral structure), and has no fine-scale structure that causes "scattering" or "resonance" effects. To keep this explanation of Fowler–Nordheim tunneling relatively simple, these assumptions are needed; but the atomic structure of matter is in effect being disregarded.
Motive energy
For an electron, the one-dimensional Schrödinger equation can be written in the form
-
()
where Ψ(x) is the electron wave-function, expressed as a function of distance x measured from the emitter's electrical surface,[62] ħ is the reduced Planck constant, m is the electron mass, U(x) is the electron potential energy, En is the total electron energy associated with motion in the x-direction, and M(x) = [U(x) − En] is called the electron motive energy.[63] M(x) can be interpreted as the negative of the electron kinetic energy associated with the motion of a hypothetical classical point electron in the x-direction, and is positive in the barrier.
The shape of a tunneling barrier is determined by how M(x) varies with position in the region where M(x) > 0. Two models have special status in field emission theory: the exact triangular (ET) barrier and the Schottky–Nordheim (SN) barrier.[64][65] These are given by equations (2) and (3), respectively:
-
()
-
()
Here h is the zero-field height (or unreduced height) of the barrier, e is the elementary positive charge, F is the barrier field, and ε0 is the electric constant. By convention, F is taken as positive, even though the classical electrostatic field would be negative. The SN equation uses the classical image potential energy to represent the physical effect "correlation and exchange".
Escape probability
For an electron approaching a given barrier from the inside, the probability of escape (or "transmission coefficient" or "penetration coefficient") is a function of h and F, and is denoted by D(h,F). The primary aim of tunneling theory is to calculate D(h,F). For physically realistic barrier models, such as the Schottky–Nordheim barrier, the Schrödinger equation cannot be solved exactly in any simple way. The following so-called "semi-classical" approach can be used. A parameter G(h,F) can be defined by the JWKB (Jeffreys-Wentzel-Kramers-Brillouin) integral:[66]
-
()
where the integral is taken across the barrier (i.e., across the region where M > 0), and the parameter g is a universal constant given by
-
()
Forbes has re-arranged a result proved by Fröman and Fröman, to show that, formally – in a one-dimensional treatment – the exact solution for D can be written[67]
-
()
where the tunneling pre-factor P can in principle be evaluated by complicated iterative integrations along a path in complex space.[67][68] In the CFE regime we have (by definition) G ≫ 1. Also, for simple models P ≈ 1. So eq. (6) reduces to the so-called simple JWKB formula:
-
()
For the exact triangular barrier, putting eq. (2) into eq. (4) yields GET = bh3/2/F, where
-
()
This parameter b is a universal constant sometimes called the second Fowler–Nordheim constant. For barriers of other shapes, we write
-
()
where ν(h,F) is a correction factor that in general has to be determined by numerical integration, using eq. (4).
Correction factor for the Schottky–Nordheim barrier
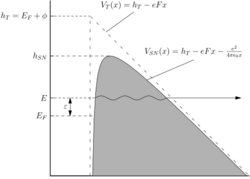
The Schottky–Nordheim barrier, which is the barrier model used in deriving the standard Fowler–Nordheim-type equation,[69] is a special case. In this case, it is known that the correction factor is a function of a single variable fh, defined by fh = F/Fh, where Fh is the field necessary to reduce the height of a Schottky–Nordheim barrier from h to 0. This field is given by
-
()
The parameter fh runs from 0 to 1, and may be called the scaled barrier field, for a Schottky–Nordheim barrier of zero-field height h.
For the Schottky–Nordheim barrier, ν(h,F) is given by the particular value ν(fh) of a function ν(ℓ′). The latter is a function of mathematical physics in its own right and has been called the principal Schottky–Nordheim barrier function. An explicit series expansion for ν(ℓ′) is derived in a 2008 paper by J. Deane.[70] The following good simple approximation for ν(fh) has been found:[69]
-
()
Decay width
The decay width (in energy), dh, measures how fast the escape probability D decreases as the barrier height h increases; dh is defined by:
-
()
When h increases by dh then the escape probability D decreases by a factor close to e ( ≈ 2.718282). For an elementary model, based on the exact triangular barrier, where we put ν = 1 and P ≈ 1, we get
The decay width dh derived from the more general expression (12) differs from this by a "decay-width correction factor" λd, so:
-
()
Usually, the correction factor can be approximated as unity.
The decay-width dF for a barrier with h equal to the local work-function φ is of special interest. Numerically this is given by:
-
()
For metals, the value of dF is typically of order 0.2 eV, but varies with barrier-field F.
Comments
A historical note is necessary. The idea that the Schottky–Nordheim barrier needed a correction factor, as in eq. (9), was introduced by Nordheim in 1928,[65] but his mathematical analysis of the factor was incorrect. A new (correct) function was introduced by Burgess, Kroemer and Houston[71] in 1953, and its mathematics was developed further by Murphy and Good in 1956.[72] This corrected function, sometimes known as a "special field emission elliptic function", was expressed as a function of a mathematical variable y known as the "Nordheim parameter". Only recently (2006 to 2008) has it been realized that, mathematically, it is much better to use the variable ℓ′ ( = y2). And only recently has it been possible to complete the definition of ν(ℓ′) by developing and proving the validity of an exact series expansion for this function (by starting from known special-case solutions of the Gauss hypergeometric differential equation). Also, approximation (11) has been found only recently. Approximation (11) outperforms, and will presumably eventually displace, all older approximations of equivalent complexity. These recent developments, and their implications, will probably have a significant impact on field emission research in due course.
The following summary brings these results together. For tunneling well below the top of a well-behaved barrier of reasonable height, the escape probability D(h,F) is given formally by:
-
()
where ν(h,F) is a correction factor that in general has to be found by numerical integration. For the special case of a Schottky–Nordheim barrier, an analytical result exists and ν(h,F) is given by ν(fh), as discussed above; approximation (11) for ν(fh) is more than sufficient for all technological purposes. The pre-factor P is also in principle a function of h and (maybe) F, but for the simple physical models discussed here it is usually satisfactory to make the approximation P = 1. The exact triangular barrier is a special case where the Schrödinger equation can be solved exactly, as was done by Fowler and Nordheim;[1] for this physically unrealistic case, ν(fh) = 1, and an analytical approximation for P exists.
The approach described here was originally developed to describe Fowler–Nordheim tunneling from smooth, classically flat, planar emitting surfaces. It is adequate for smooth, classical curved surfaces of radii down to about 10 to 20 nm. It can be adapted to surfaces of sharper radius, but quantities such as ν and D then become significant functions of the parameter(s) used to describe the surface curvature. When the emitter is so sharp that atomic-level detail cannot be neglected, and/or the tunneling barrier is thicker than the emitter-apex dimensions, then a more sophisticated approach is desirable.
As noted at the beginning, the effects of the atomic structure of materials are disregarded in the relatively simple treatments of field electron emission discussed here. Taking atomic structure properly into account is a very difficult problem, and only limited progress has been made.[33] However, it seems probable that the main influences on the theory of Fowler–Nordheim tunneling will (in effect) be to change the values of P and ν in eq. (15), by amounts that cannot easily be estimated at present.
All these remarks apply in principle to Fowler Nordheim tunneling from any conductor where (before tunneling) the electrons may be treated as in travelling-wave states. The approach may be adapted to apply (approximately) to situations where the electrons are initially in localized states at or very close inside the emitting surface, but this is beyond the scope of this article.
Total-energy distribution
The energy distribution of the emitted electrons is important both for scientific experiments that use the emitted electron energy distribution to probe aspects of the emitter surface physics[34] and for the field emission sources used in electron beam instruments such as electron microscopes.[42] In the latter case, the "width" (in energy) of the distribution influences how finely the beam can be focused.
The theoretical explanation here follows the approach of Forbes.[73] If ε denotes the total electron energy relative to the emitter Fermi level, and Kp denotes the kinetic energy of the electron parallel to the emitter surface, then the electron's normal energy εn (sometimes called its "forwards energy") is defined by
-
()
Two types of theoretical energy distribution are recognized: the normal-energy distribution (NED), which shows how the energy εn is distributed immediately after emission (i.e., immediately outside the tunneling barrier); and the total-energy distribution, which shows how the total energy ε is distributed. When the emitter Fermi level is used as the reference zero level, both ε and εn can be either positive or negative.
Energy analysis experiments have been made on field emitters since the 1930s. However, only in the late 1950s was it realized (by Young and Mueller[31] [,YM58]) that these experiments always measured the total energy distribution, which is now usually denoted by j(ε). This is also true (or nearly true) when the emission comes from a small field enhancing protrusion on an otherwise flat surface.[34]
To see how the total energy distribution can be calculated within the framework of a Sommerfeld free-electron-type model, look at the P-T energy-space diagram (P-T="parallel-total").
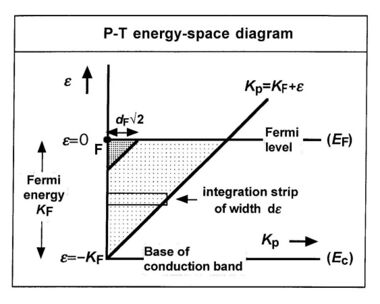
This shows the "parallel kinetic energy" Kp on the horizontal axis and the total energy ε on the vertical axis. An electron inside the bulk metal usually has values of Kp and ε that lie within the lightly shaded area. It can be shown that each element dεdKp of this energy space makes a contribution to the electron current density incident on the inside of the emitter boundary.[73] Here, zS is the universal constant (called here the Sommerfeld supply density):
-
()
and is the Fermi–Dirac distribution function:
-
()
where T is thermodynamic temperature and kB is the Boltzmann constant.
This element of incident current density sees a barrier of height h given by:
-
()
The corresponding escape probability is D(h,F): this may be expanded (approximately) in the form[73]
-
()
where DF is the escape probability for a barrier of unreduced height equal to the local work-function φ. Hence, the element dεdKp makes a contribution to the emission current density, and the total contribution made by incident electrons with energies in the elementary range dε is thus
-
()
where the integral is in principle taken along the strip shown in the diagram, but can in practice be extended to ∞ when the decay-width dF is very much less than the Fermi energy KF (which is always the case for a metal). The outcome of the integration can be written:
-
()
where and are values appropriate to a barrier of unreduced height h equal to the local work function φ, and is defined by this equation.
For a given emitter, with a given field applied to it, is independent of F, so eq. (21) shows that the shape of the distribution (as ε increases from a negative value well below the Fermi level) is a rising exponential, multiplied by the FD distribution function. This generates the familiar distribution shape first predicted by Young.[31] At low temperatures, goes sharply from 1 to 0 in the vicinity of the Fermi level, and the FWHM of the distribution is given by:
-
()
The fact that experimental CFE total energy distributions have this basic shape is a good experimental confirmation that electrons in metals obey Fermi–Dirac statistics.
Cold field electron emission
Fowler–Nordheim-type equations
Introduction
Fowler–Nordheim-type equations, in the J-F form, are (approximate) theoretical equations derived to describe the local current density J emitted from the internal electron states in the conduction band of a bulk metal. The emission current density (ECD) J for some small uniform region of an emitting surface is usually expressed as a function J(φ,F) of the local work-function φ and the local barrier field F that characterize the small region. For sharply curved surfaces, J may also depend on the parameter(s) used to describe the surface curvature.
Owing to the physical assumptions made in the original derivation,[1] the term Fowler–Nordheim-type equation has long been used only for equations that describe the ECD at zero temperature. However, it is better to allow this name to include the slightly modified equations (discussed below) that are valid for finite temperatures within the CFE emission regime.
Zero-temperature form
Current density is best measured in A/m2. The total current density emitted from a small uniform region can be obtained by integrating the total energy distribution j(ε) with respect to total electron energy ε. At zero temperature, the Fermi–Dirac distribution function fFD = 1 for ε<0, and fFD = 0 for ε>0. So the ECD at 0 K, J0, is given from eq. (18) by
-
()
where is the effective supply for state F, and is defined by this equation. Strictly, the lower limit of the integral should be −KF, where KF is the Fermi energy; but if dF is very much less than KF (which is always the case for a metal) then no significant contribution to the integral comes from energies below KF, and it can formally be extended to –∞.
Result (23) can be given a simple and useful physical interpretation by referring to Fig. 1. The electron state at point "F" on the diagram ("state F") is the "forwards moving state at the Fermi level" (i.e., it describes a Fermi-level electron moving normal to and towards the emitter surface). At 0 K, an electron in this state sees a barrier of unreduced height φ, and has an escape probability DF that is higher than that for any other occupied electron state. So it is convenient to write J0 as ZFDF, where the "effective supply" ZF is the current density that would have to be carried by state F inside the metal if all of the emission came out of state F.
In practice, the current density mainly comes out of a group of states close in energy to state F, most of which lie within the heavily shaded area in the energy-space diagram. Since, for a free-electron model, the contribution to the current density is directly proportional to the area in energy space (with the Sommerfeld supply density zS as the constant of proportionality), it is useful to think of the ECD as drawn from electron states in an area of size dF2 (measured in eV2) in the energy-space diagram. That is, it is useful to think of the ECD as drawn from states in the heavily shaded area in Fig. 1. (This approximation gets slowly worse as temperature increases.)
ZF can also be written in the form:
-
()
where the universal constant a, sometimes called the First Fowler–Nordheim Constant, is given by
-
()
This shows clearly that the pre-exponential factor a φ−1F2, that appears in Fowler–Nordheim-type equations, relates to the effective supply of electrons to the emitter surface, in a free-electron model.
Non-zero temperatures
To obtain a result valid for non-zero temperature, we note from eq. (23) that zSdFDF = J0/dF. So when eq. (21) is integrated at non-zero temperature, then – on making this substitution, and inserting the explicit form of the Fermi–Dirac distribution function – the ECD J can be written in the form:
-
()
where λT is a temperature correction factor given by the integral. The integral can be transformed, by writing and , and then , into the standard result:[74]
-
()
This is valid for w>1 (i.e., dF/kBT > 1). Hence – for temperatures such that kBT<dF:
-
()
where the expansion is valid only if (πkBT /dF) ≪ 1. An example value (for φ= 4.5 eV, F= 5 V/nm, T= 300 K) is λT= 1.024. Normal thinking has been that, in the CFE regime, λT is always small in comparison with other uncertainties, and that it is usually unnecessary to explicitly include it in formulae for the current density at room temperature.
The emission regimes for metals are, in practice, defined, by the ranges of barrier field F and temperature T for which a given family of emission equations is mathematically adequate. When the barrier field F is high enough for the CFE regime to be operating for metal emission at 0 K, then the condition kBT<dF provides a formal upper bound (in temperature) to the CFE emission regime. However, it has been argued that (due to approximations made elsewhere in the derivation) the condition kBT<0.7dF is a better working limit: this corresponds to a λT-value of around 1.09, and (for the example case) an upper temperature limit on the CFE regime of around 1770 K. This limit is a function of barrier field.[33][72]
Note that result (28) here applies for a barrier of any shape (though dF will be different for different barriers).
Physically complete Fowler–Nordheim-type equation
Result (23) also leads to some understanding of what happens when atomic-level effects are taken into account, and the band-structure is no longer free-electron like. Due to the presence of the atomic ion-cores, the surface barrier, and also the electron wave-functions at the surface, will be different. This will affect the values of the correction factor , the prefactor P, and (to a limited extent) the correction factor λd. These changes will, in turn, affect the values of the parameter DF and (to a limited extent) the parameter dF. For a real metal, the supply density will vary with position in energy space, and the value at point "F" may be different from the Sommerfeld supply density. We can take account of this effect by introducing an electronic-band-structure correction factor λB into eq. (23). Modinos has discussed how this factor might be calculated: he estimates that it is most likely to be between 0.1 and 1; it might lie outside these limits but is most unlikely to lie outside the range 0.01<λB<10.[75]
By defining an overall supply correction factor λZ equal to λT λB λd2, and combining equations above, we reach the so-called physically complete Fowler–Nordheim-type equation:[76]
-
()
where [=(φ,F)] is the exponent correction factor for a barrier of unreduced height φ. This is the most general equation of the Fowler–Nordheim type. Other equations in the family are obtained by substituting specific expressions for the three correction factors , PF and λZ it contains. The so-called elementary Fowler–Nordheim-type equation, that appears in undergraduate textbook discussions of field emission, is obtained by putting λZ→1, PF→1, →1; this does not yield good quantitative predictions because it makes the barrier stronger than it is in physical reality. The so-called standard Fowler–Nordheim-type equation, originally developed by Murphy and Good,[72] and much used in past literature, is obtained by putting λZ→tF−2, PF→1, →vF, where vF is v(f), where f is the value of fh obtained by putting h=φ, and tF is a related parameter (of value close to unity).[69]
Within the more complete theory described here, the factor tF−2 is a component part of the correction factor λd2 [see,[67] and note that λd2 is denoted by λD there]. There is no significant value in continuing the separate identification of tF−2. Probably, in the present state of knowledge, the best approximation for simple Fowler–Nordheim-type equation based modeling of CFE from metals is obtained by putting λZ→1, PF → 1, → v(f). This re-generates the Fowler–Nordheim-type equation used by Dyke and Dolan in 1956, and can be called the "simplified standard Fowler–Nordheim-type equation".
Recommended form for simple Fowler–Nordheim-type calculations
Explicitly, this recommended simplified standard Fowler–Nordheim-type equation, and associated formulae, are:
-
()
-
()
-
()
-
()
where Fφ here is the field needed to reduce to zero a Schottky–Nordheim barrier of unreduced height equal to the local work-function φ, and f is the scaled barrier field for a Schottky–Nordheim barrier of unreduced height φ. [This quantity f could have been written more exactly as fφSN, but it makes this Fowler–Nordheim-type equation look less cluttered if the convention is adopted that simple f means the quantity denoted by fφSN in,[69] eq. (2.16).] For the example case (φ= 4.5 eV, F= 5 V/nm), f≈ 0.36 and v(f) ≈ 0.58; practical ranges for these parameters are discussed further in.[77]
Note that the variable f (the scaled barrier field) is not the same as the variable y (the Nordheim parameter) extensively used in past field emission literature, and that " v(f) " does NOT have the same mathematical meaning and values as the quantity " v(y) " that appears in field emission literature. In the context of the revised theory described here, formulae for v(y), and tables of values for v(y) should be disregarded, or treated as values of v(f1/2). If more exact values for v(f) are required, then[69] provides formulae that give values for v(f) to an absolute mathematical accuracy of better than 8×10−10. However, approximation formula (30c) above, which yields values correct to within an absolute mathematical accuracy of better 0.0025, should gives values sufficiently accurate for all technological purposes.[69]
Comments
A historical note on methods of deriving Fowler–Nordheim-type equations is necessary. There are several possible approaches to deriving these equations, using free-electron theory. The approach used here was introduced by Forbes in 2004 and may be described as "integrating via the total energy distribution, using the parallel kinetic energy Kp as the first variable of integration".[73] Basically, it is a free-electron equivalent of the Modinos procedure[33][75] (in a more advanced quantum-mechanical treatment) of "integrating over the surface Brillouin zone". By contrast, the free-electron treatments of CFE by Young in 1959,[31] Gadzuk and Plummer in 1973[34] and Modinos in 1984,[33] also integrate via the total energy distribution, but use the normal energy εn (or a related quantity) as the first variable of integration.
There is also an older approach, based on a seminal paper by Nordheim in 1928,[78] that formulates the problem differently and then uses first Kp and then εn (or a related quantity) as the variables of integration: this is known as "integrating via the normal-energy distribution". This approach continues to be used by some authors. Although it has some advantages, particularly when discussing resonance phenomena, it requires integration of the Fermi–Dirac distribution function in the first stage of integration: for non-free-electron-like electronic band-structures this can lead to very complex and error-prone mathematics (as in the work of Stratton on semiconductors).[79] Further, integrating via the normal-energy distribution does not generate experimentally measured electron energy distributions.
In general, the approach used here seems easier to understand, and leads to simpler mathematics.
It is also closer in principle to the more sophisticated approaches used when dealing with real bulk crystalline solids, where the first step is either to integrate contributions to the ECD over constant energy surfaces in a wave-vector space (k -space),[34] or to integrate contributions over the relevant surface Brillouin zone.[33] The Forbes approach is equivalent either to integrating over a spherical surface in k -space, using the variable Kp to define a ring-like integration element that has cylindrical symmetry about an axis in a direction normal to the emitting surface, or to integrating over an (extended) surface Brillouin zone using circular-ring elements.
CFE theoretical equations
The preceding section explains how to derive Fowler–Nordheim-type equations. Strictly, these equations apply only to CFE from bulk metals. The ideas in the following sections apply to CFE more generally, but eq. (30) will be used to illustrate them.
For CFE, basic theoretical treatments provide a relationship between the local emission current density J and the local barrier field F, at a local position on the emitting surface. Experiments measure the emission current i from some defined part of the emission surface, as a function of the voltage V applied to some counter-electrode. To relate these variables to J and F, auxiliary equations are used.
The voltage-to-barrier-field conversion factor β is defined by:
-
()
The value of F varies from position to position on an emitter surface, and the value of β varies correspondingly.
For a metal emitter, the β−value for a given position will be constant (independent of voltage) under the following conditions: (1) the apparatus is a "diode" arrangement, where the only electrodes present are the emitter and a set of "surroundings", all parts of which are at the same voltage; (2) no significant field-emitted vacuum space-charge (FEVSC) is present (this will be true except at very high emission current densities, around 109 A/m2 or higher[27][80]); (3) no significant "patch fields" exist,[63] as a result of non-uniformities in local work-function (this is normally assumed to be true, but may not be in some circumstances). For non-metals, the physical effects called "field penetration" and "band bending" [M084] can make β a function of applied voltage, although – surprisingly – there are few studies of this effect.
The emission current density J varies from position to position across the emitter surface. The total emission current i from a defined part of the emitter is obtained by integrating J across this part. To obtain a simple equation for i(V), the following procedure is used. A reference point "r" is selected within this part of the emitter surface (often the point at which the current density is highest), and the current density at this reference point is denoted by Jr. A parameter Ar, called the notional emission area (with respect to point "r"), is then defined by:
-
()
where the integral is taken across the part of the emitter of interest.
This parameter Ar was introduced into CFE theory by Stern, Gossling and Fowler in 1929 (who called it a "weighted mean area").[16] For practical emitters, the emission current density used in Fowler–Nordheim-type equations is always the current density at some reference point (though this is usually not stated). Long-established convention denotes this reference current density by the simple symbol J, and the corresponding local field and conversion factor by the simple symbols F and β, without the subscript "r" used above; in what follows, this convention is used.
The notional emission area Ar will often be a function of the reference local field (and hence voltage),[30] and in some circumstances might be a significant function of temperature.
Because Ar has a mathematical definition, it does not necessarily correspond to the area from which emission is observed to occur from a single-point emitter in a field electron (emission) microscope. With a large-area emitter, which contains many individual emission sites, Ar will nearly always be very very[clarification needed] much less than the "macroscopic" geometrical area (AM) of the emitter as observed visually (see below).
Incorporating these auxiliary equations into eq. (30a) yields
-
()
This is the simplified standard Fowler–Nordheim-type equation, in i-V form. The corresponding "physically complete" equation is obtained by multiplying by λZPF.
Modified equations for large-area emitters
The equations in the preceding section apply to all field emitters operating in the CFE regime. However, further developments are useful for large-area emitters that contain many individual emission sites.
For such emitters, the notional emission area will nearly always be very very[clarification needed] much less than the apparent "macroscopic" geometrical area (AM) of the physical emitter as observed visually. A dimensionless parameter αr, the area efficiency of emission, can be defined by
-
()
Also, a "macroscopic" (or "mean") emission current density JM (averaged over the geometrical area AM of the emitter) can be defined, and related to the reference current density Jr used above, by
-
()
This leads to the following "large-area versions" of the simplified standard Fowler–Nordheim-type equation:
-
()
-
()
Both these equations contain the area efficiency of emission αr. For any given emitter this parameter has a value that is usually not well known. In general, αr varies greatly as between different emitter materials, and as between different specimens of the same material prepared and processed in different ways. Values in the range 10−10 to 10−6 appear to be likely, and values outside this range may be possible.
The presence of αr in eq. (36) accounts for the difference between the macroscopic current densities often cited in the literature (typically 10 A/m2 for many forms of large-area emitter other than Spindt arrays[50]) and the local current densities at the actual emission sites, which can vary widely but which are thought to be generally of the order of 109 A/m2, or possibly slightly less.
A significant part of the technological literature on large-area emitters fails to make clear distinctions between local and macroscopic current densities, or between notional emission area Ar and macroscopic area AM, and/or omits the parameter αr from cited equations. Care is necessary in order to avoid errors of interpretation.
It is also sometimes convenient to split the conversion factor βr into a "macroscopic part" that relates to the overall geometry of the emitter and its surroundings, and a "local part" that relates to the ability of the very-local structure of the emitter surface to enhance the electric field. This is usually done by defining a "macroscopic field" FM that is the field that would be present at the emitting site in the absence of the local structure that causes enhancement. This field FM is related to the applied voltage by a "voltage-to-macroscopic-field conversion factor" βM defined by:
-
()
In the common case of a system comprising two parallel plates, separated by a distance W, with emitting nanostructures created on one of them, βM = 1/W.
A "field enhancement factor" γ is then defined and related to the values of βr and βM by
-
()
With eq. (31), this generates the following formulae:
-
()
-
()
where, in accordance with the usual convention, the suffix "r" has now been dropped from parameters relating to the reference point. Formulae exist for the estimation of γ, using classical electrostatics, for a variety of emitter shapes, in particular the "hemisphere on a post".[81]
Equation (40) implies that versions of Fowler–Nordheim-type equations can be written where either F or βV is everywhere replaced by . This is often done in technological applications where the primary interest is in the field enhancing properties of the local emitter nanostructure. However, in some past work, failure to make a clear distinction between barrier field F and macroscopic field FM has caused confusion or error.
More generally, the aims in technological development of large-area field emitters are to enhance the uniformity of emission by increasing the value of the area efficiency of emission αr, and to reduce the "onset" voltage at which significant emission occurs, by increasing the value of β. Eq. (41) shows that this can be done in two ways: either by trying to develop "high-γ" nanostructures, or by changing the overall geometry of the system so that βM is increased. Various trade-offs and constraints exist.
In practice, although the definition of macroscopic field used above is the commonest one, other (differently defined) types of macroscopic field and field enhancement factor are used in the literature, particularly in connection with the use of probes to investigate the i-V characteristics of individual emitters.[82]
In technological contexts field-emission data are often plotted using (a particular definition of) FM or 1/FM as the x-coordinate. However, for scientific analysis it usually better not to pre-manipulate the experimental data, but to plot the raw measured i-V data directly. Values of technological parameters such as (the various forms of) γ can then be obtained from the fitted parameters of the i-V data plot (see below), using the relevant definitions.
Modified equations for nanometrically sharp emitters
Most of the theoretical derivations in the field emission theory are done under the assumption that the barrier takes the Schottky–Nordheim form eq. (3). However, this barrier form is not valid for emitters with radii of curvature comparable to the length of the tunnelling barrier. The latter depends on the work function and the field, but in cases of practical interest, the SN barrier approximation can be considered valid for emitters with radii , as explained in the next paragraph.
The main assumption of the SN barrier approximation is that the electrostatic potential term takes the linear form in the tunnelling region. The latter has been proved to hold only if .[83] Therefore, if the tunnelling region has a length , for all that determines the tunnelling process; thus if eq. (1) holds and the SN barrier approximation is valid. If the tunnelling probability is high enough to produce measurable field emission, L does not exceed 1-2 nm. Hence, the SN barrier is valid for emitters with radii of the order of some tens of nm.
However, modern emitters are much sharper than this, with radii that of the order of a few nm. Therefore, the standard FN equation, or any version of it that assumes the SN barrier, leads to significant errors for such sharp emitters. This has been both shown theoretically[84][85] and confirmed experimentally.[86]
The above problem was tackled by Kyritsakis and Xanthakis,[83] who generalized the SN barrier by including the electrostatic effects of the emitter curvature. The general barrier form for an emitter with radius of average curvature
(inverse of the average of the two principal curvatures) can be asymptotically expanded as[87]
-
.
()
After neglecting all terms, and employing the JWKB approximation (4) for this barrier, the Gamow exponent takes a form that generalizes eq. (5)
-
()
where is defined by (30d), is given by (30c) and is a new function that can be approximated in a similar manner as (30c) (there are typographical mistakes in ref.,[83] corrected here):
-
()
Given the expression for the Gamow exponent as a function of the field-free barrier height , the emitted current density for cold field emission can be obtained from eq. (23). It yields
-
()
where the functions and are defined as
-
()
and
-
()
In equation (46), for completeness purposes, is not approximated by unity as in (29) and (30a), although for most practical cases it is a very good approximation. Apart from this, equations (43), (44) and (46) coincide with the corresponding ones of the standard Fowler–Nordheim theory (3), (9), and (30a), in the limit ; this is expected since the former equations generalise the latter.
Finally, note that the above analysis is asymptotic in the limit , similarly to the standard Fowler–Nordheim theory using the SN barrier. However, the addition of the quadratic terms renders it significantly more accurate for emitters with radii of curvature in the range ~5–20 nm. For sharper emitters there is no general approximation for the current density. In order to obtain the current density, one has to calculate the electrostatic potential and evaluate the JWKB integral numerically. For this purpose, scientific computing software has been developed (see e.g. GETELEC[88]).
Empirical CFE i–V equation
At the present stage of CFE theory development, it is important to make a distinction between theoretical CFE equations and an empirical CFE equation. The former are derived from condensed matter physics (albeit in contexts where their detailed development is difficult). An empirical CFE equation, on the other hand, simply attempts to represent the actual experimental form of the dependence of current i on voltage V.
In the 1920s, empirical equations were used to find the power of V that appeared in the exponent of a semi-logarithmic equation assumed to describe experimental CFE results. In 1928, theory and experiment were brought together to show that (except, possibly, for very sharp emitters) this power is V−1. It has recently been suggested that CFE experiments should now be carried out to try to find the power (κ) of V in the pre-exponential of the following empirical CFE equation:[89]
-
()
where B, C and κ are treated as constants.
From eq. (42) it is readily shown that
-
()
In the 1920s, experimental techniques could not distinguish between the results κ = 0 (assumed by Millikan and Laurtisen)[13] and κ = 2 (predicted by the original Fowler–Nordheim-type equation).[1] However, it should now be possible to make reasonably accurate measurements of dlni/d(1/V) (if necessary by using lock-in amplifier/phase-sensitive detection techniques and computer-controlled equipment), and to derive κ from the slope of an appropriate data plot.[50]
Following the discovery of approximation (30b), it is now very clear that – even for CFE from bulk metals – the value κ=2 is not expected. This can be shown as follows. Using eq. (30c) above, a dimensionless parameter η may be defined by
-
()
For φ = 4.50 eV, this parameter has the value η = 4.64. Since f = F/Fφ and v(f) is given by eq (30b), the exponent in the simplified standard Fowler–Nordheim-type equation (30) can be written in an alternative form and then expanded as follows:[69]
-
()
Provided that the conversion factor β is independent of voltage, the parameter f has the alternative definition f = V/Vφ, where Vφ is the voltage needed, in a particular experimental system, to reduce the height of a Schottky–Nordheim barrier from φ to zero. Thus, it is clear that the factor v(f) in the exponent of the theoretical equation (30) gives rise to additional V-dependence in the pre-exponential of the empirical equation. Thus, (for effects due to the Schottky–Nordheim barrier, and for an emitter with φ=4.5 eV) we obtain the prediction:
-
()
Since there may also be voltage dependence in other factors in a Fowler–Nordheim-type equation, in particular in the notional emission area[30] Ar and in the local work-function, it is not necessarily expected that κ for CFE from a metal of local work-function 4.5 eV should have the value κ = 1.23, but there is certainly no reason to expect that it will have the original Fowler–Nordheim value κ = 2.[90]
A first experimental test of this proposal has been carried out by Kirk, who used a slightly more complex form of data analysis to find a value 1.36 for his parameter κ. His parameter κ is very similar to, but not quite the same as, the parameter κ used here, but nevertheless his results do appear to confirm the potential usefulness of this form of analysis.[91]
Use of the empirical CFE equation (42), and the measurement of κ, may be of particular use for non-metals. Strictly, Fowler–Nordheim-type equations apply only to emission from the conduction band of bulk crystalline solids. However, empirical equations of form (42) should apply to all materials (though, conceivably, modification might be needed for very sharp emitters). It seems very likely that one way in which CFE equations for newer materials may differ from Fowler–Nordheim-type equations is that these CFE equations may have a different power of F (or V) in their pre-exponentials. Measurements of κ might provide some experimental indication of this.
Fowler–Nordheim plots and Millikan–Lauritsen plots
The original theoretical equation derived by Fowler and Nordheim[1] has, for the last 80 years, influenced the way that experimental CFE data has been plotted and analyzed. In the very widely used Fowler–Nordheim plot, as introduced by Stern et al. in 1929,[16] the quantity ln{i/V2} is plotted against 1/V. The original thinking was that (as predicted by the original or the elementary Fowler–Nordheim-type equation) this would generate an exact straight line of slope SFN. SFN would be related to the parameters that appear in the exponent of a Fowler–Nordheim-type equation of i-V form by:
-
()
Hence, knowledge of φ would allow β to be determined, or vice versa.
[In principle, in system geometries where there is local field-enhancing nanostructure present, and the macroscopic conversion factor βM can be determined, knowledge of β then allows the value of the emitter's effective field enhancement factor γ to be determined from the formula γ = β/βM. In the common case of a film emitter generated on one plate of a two-plate arrangement with plate-separation W (so βM = 1/W) then
-
()
Nowadays, this is one of the most likely applications of Fowler–Nordheim plots.]
It subsequently became clear that the original thinking above is strictly correct only for the physically unrealistic situation of a flat emitter and an exact triangular barrier. For real emitters and real barriers a "slope correction factor" σFN has to be introduced, yielding the revised formula
-
()
The value of σFN will, in principle, be influenced by any parameter in the physically complete Fowler–Nordheim-type equation for i(V) that has a voltage dependence.
At present, the only parameter that is considered important is the correction factor relating to the barrier shape, and the only barrier for which there is any well-established detailed theory is the Schottky–Nordheim barrier. In this case, σFN is given by a mathematical function called s. This function s was first tabulated correctly (as a function of the Nordheim parameter y) by Burgess, Kroemer and Houston in 1953;[71] and a modern treatment that gives s as function of the scaled barrier field f for a Schottky–Nordheim barrier is given in.[69] However, it has long been clear that, for practical emitter operation, the value of s lies in the range 0.9 to 1.
In practice, due to the extra complexity involved in taking the slope correction factor into detailed account, many authors (in effect) put σFN = 1 in eq. (49), thereby generating a systematic error in their estimated values of β and/or γ, thought usually to be around 5%.
However, empirical equation (42) – which in principle is more general than Fowler–Nordheim-type equations – brings with it possible new ways of analyzing field emission i-V data. In general, it may be assumed that the parameter B in the empirical equation is related to the unreduced height H of some characteristic barrier seen by tunneling electrons by
-
()
(In most cases, but not necessarily all, H would be equal to the local work-function; certainly this is true for metals.) The issue is how to determine the value of B by experiment. There are two obvious ways. (1) Suppose that eq. (43) can be used to determine a reasonably accurate experimental value of κ, from the slope of a plot of form [−dln{i}/d(1/V) vs. V]. In this case, a second plot, of ln(i)/Vκ vs. 1/V, should be an exact straight line of slope −B. This approach should be the most accurate way of determining B.
(2) Alternatively, if the value of κ is not exactly known, and cannot be accurately measured, but can be estimated or guessed, then a value for B can be derived from a plot of the form [ln{i} vs. 1/V]. This is the form of plot used by Millikan and Lauritsen in 1928. Rearranging eq. (43) gives
-
()
Thus, B can be determined, to a good degree of approximation, by determining the mean slope of a Millikan–Lauritsen plot over some range of values of 1/V, and by applying a correction, using the value of 1/V at the midpoint of the range and an assumed value of κ.
The main advantages of using a Millikan–Lauritsen plot, and this form of correction procedure, rather than a Fowler–Nordheim plot and a slope correction factor, are seen to be the following. (1) The plotting procedure is marginally more straightforward. (2) The correction involves a physical parameter (V) that is a measured quantity, rather than a physical parameter (f) that has to be calculated [in order to then calculate a value of s(f) or, more generally σFN(f)]. (3) Both the parameter κ itself, and the correction procedure, are more transparent (and more readily understood) than the Fowler–Nordheim-plot equivalents. (4) This procedure takes into account all physical effects that influence the value of κ, whereas the Fowler–Nordheim-plot correction procedure (in the form in which it has been carried out for the last 50 years) takes into account only those effects associated with barrier shape – assuming, furthermore, that this shape is that of a Schottky–Nordheim barrier. (5) There is a cleaner separation of theoretical and technological concerns: theoreticians will be interested in establishing what information any measured values of κ provide about CFE theory; but experimentalists can simply use measured values of κ to make more accurate estimates (if needed) of field enhancement factors.[citation needed]
This correction procedure for Millikan–Lauritsen plots will become easier to apply when a sufficient number of measurements of κ have been made, and a better idea is available of what typical values actually are. At present, it seems probable that for most materials κ will lie in the range -1<κ<3.[citation needed]
Further theoretical information
Developing the approximate theory of CFE from metals above is comparatively easy, for the following reasons. (1) Sommerfeld's free-electron theory, with its particular assumptions about the distribution of internal electron states in energy, applies adequately to many metals as a first approximation. (2) Most of the time, metals have no surface states and (in many cases) metal wave-functions have no significant "surface resonances". (3) Metals have a high density of states at the Fermi level, so the charge that generates/screens external electric fields lies mainly on the outside of the top atomic layer, and no meaningful "field penetration" occurs. (4) Metals have high electrical conductivity: no significant voltage drops occur inside metal emitters: this means that there are no factors obstructing the supply of electrons to the emitting surface, and that the electrons in this region can be both in effective local thermodynamic equilibrium and in effective thermodynamic equilibrium with the electrons in the metal support structure on which the emitter is mounted. (5) Atomic-level effects are disregarded.[citation needed]
The development of "simple" theories of field electron emission, and in particular the development of Fowler–Nordheim-type equations, relies on all five of the above factors being true. For materials other than metals (and for atomically sharp metal emitters) one or more of the above factors will be untrue. For example, crystalline semiconductors do not have a free-electron-like band-structure, do have surface states, are subject to field penetration and band bending, and may exhibit both internal voltage drops and statistical decoupling of the surface-state electron distribution from the electron distribution in the surface region of the bulk band-structure (this decoupling is known as "the Modinos effect").[33][92]
In practice, the theory of the actual Fowler–Nordheim tunneling process is much the same for all materials (though details of barrier shape may vary, and modified theory has to be developed for initial states that are localized rather than are travelling-wave-like). However, notwithstanding such differences, one expects (for thermodynamic equilibrium situations) that all CFE equations will have exponents that behave in a generally similar manner. This is why applying Fowler–Nordheim-type equations to materials outside the scope of the derivations given here often works. If interest is only in parameters (such as field enhancement factor) that relate to the slope of Fowler–Nordheim or Millikan–Lauritsen plots and to the exponent of the CFE equation, then Fowler–Nordheim-type theory will often give sensible estimates. However, attempts to derive meaningful current density values will usually or always fail.
Note that a straight line in a Fowler–Nordheim or Millikan–Lauritsen plot does not indicate that emission from the corresponding material obeys a Fowler–Nordheim-type equation: it indicates only that the emission mechanism for individual electrons is probably Fowler–Nordheim tunneling.[citation needed]
Different materials may have radically different distributions in energy of their internal electron states, so the process of integrating current-density contributions over the internal electron states may give rise to significantly different expressions for the current-density pre-exponentials, for different classes of material. In particular, the power of barrier field appearing in the pre-exponential may be different from the original Fowler–Nordheim value "2". Investigation of effects of this kind is an active research topic. Atomic-level "resonance" and "scattering" effects, if they occur, will also modify the theory.
Where materials are subject to field penetration and band bending, a necessary preliminary is to have good theories of such effects (for each different class of material) before detailed theories of CFE can be developed. Where voltage-drop effects occur, then the theory of the emission current may, to a greater or lesser extent, become theory that involves internal transport effects, and may become very complex.
See also
- Field-emission microscope
- Field emission probes
- Field emitter array
- Field-emission display
- Franz–Keldysh effect
References
- ↑ 1.0 1.1 1.2 1.3 1.4 1.5 Fowler, R.H.; Dr. L. Nordheim (1928-05-01). "Electron Emission in Intense Electric Fields". Proceedings of the Royal Society A 119 (781): 173–181. doi:10.1098/rspa.1928.0091. Bibcode: 1928RSPSA.119..173F. http://www-project.slac.stanford.edu/lc/wkshp/RFBreakdwn/references/fowler.pdf. Retrieved 2009-10-26.
- ↑ Winkler, J.H. (1744). Gedanken von den Eigenschaften, Wirkungen und Ursachen der Electricität nebst Beschreibung zweiner electrischer Maschinen. Leipzig: Book Chapter Breitkopf.
- ↑ Thomson, J.J. (October 1897). "Cathode Rays". Phil. Mag.. 5th series 44 (269): 293–316. doi:10.1080/14786449708621070. https://zenodo.org/records/1431235/files/article.pdf.
- ↑ Richardson, O.W. (1916). The Emission of Electricity from Hot Bodies. London: Longmans.
- ↑ Einstein, A. (1905). "On a heuristic point of view about the creation and conversion of light". Ann. Phys. Chem. 17 (6): 132–148. doi:10.1002/andp.19053220607. Bibcode: 1905AnP...322..132E.
- ↑ 6.0 6.1 Richardson, O.W. (1929). "Thermionic phenomena and the laws which govern them". Nobel Lectures, Physics 1922-1941. https://www.nobelprize.org/physics/laureates/1928/richardson-lecture.pdf. Retrieved 2009-10-25.
- ↑ 7.0 7.1 7.2 Lilienfeld, J. E. (1922). Am. J. Roentgenol. 9: 192.
- ↑ Kleint, C. (1993). "On the early history of field emission including attempts of tunneling spectroscopy". Progress in Surface Science 42 (1–4): 101–115. doi:10.1016/0079-6816(93)90064-3. Bibcode: 1993PrSS...42..101K.
- ↑ Kleint, C. (2004). "Comments and references relating to early work in field electron emission". Surface and Interface Analysis 36 (56): 387–390. doi:10.1002/sia.1894.
- ↑ 10.0 10.1 10.2 10.3 Millikan, R.A.; Eyring, C.F. (1926). "Laws governing the pulling of electrons out of metals under intense electrical fields". Phys. Rev. 27 (1): 51–67. doi:10.1103/PhysRev.27.51. Bibcode: 1926PhRv...27...51M. http://resolver.caltech.edu/CaltechAUTHORS:MILpr26d.
- ↑ Gossling, B. S. (1926). "The emission of electrons under the influence of intense electric fields". Phil. Mag.. 7th series 1 (3): 609–635. doi:10.1080/14786442608633662.
- ↑ Schottky, W. (December 1923). "Über kalte und warme Elektronenentladungen". Zeitschrift für Physik A 14 (63): 63–106. doi:10.1007/bf01340034. Bibcode: 1923ZPhy...14...63S.
- ↑ 13.0 13.1 13.2 Millikan, R.A.; Lauritsen, C.C. (1928). "Relations of field-currents to thermionic-currents". PNAS 14 (1): 45–49. doi:10.1073/pnas.14.1.45. PMID 16587302. Bibcode: 1928PNAS...14...45M.
- ↑ 14.0 14.1 Oppenheimer, J.R. (1928). "Three notes on the quantum theory of aperiodic effects". Physical Review 31 (1): 66–81. doi:10.1103/PhysRev.31.66. Bibcode: 1928PhRv...31...66O.
- ↑ Yamabe, T.; Tachibana, A.; Silverstone, H.J. (1977). "Theory of the ionization of the hydrogen atom by an external electrostatic field". Physical Review A 16 (3): 877–890. doi:10.1103/PhysRevA.16.877. Bibcode: 1977PhRvA..16..877Y.
- ↑ 16.0 16.1 16.2 Stern, T.E.; Gossling, B.S.; Fowler, R.H. (1929). "Further studies in the emission of electrons from cold metals". Proceedings of the Royal Society A 124 (795): 699–723. doi:10.1098/rspa.1929.0147. Bibcode: 1929RSPSA.124..699S.
- ↑ Sommerfeld, A. (1927). "Zur Elektronentheorie der Metalle". Naturwissenschaften 15 (41): 825. doi:10.1007/BF01505083. Bibcode: 1927NW.....15..825S.
- ↑ 18.0 18.1 Sommerfeld, A.; Beth, H. (1963). "Handbuch der Physik". Julius Springer-Verlag 24.
- ↑ Z. Physik 51, 204 (1928) G. Gamow, "Zur Quantentheorie des Atomkernes".
- ↑ Gurney, R.W.; Condon, E.U. (1928). "Wave mechanics and radioactive disintegration". Nature 122 (3073): 439. doi:10.1038/122439a0. Bibcode: 1928Natur.122..439G.
- ↑ Gurney, R.W.; Condon, E.U. (1929). "Quantum mechanics and radioactive disintegration". Physical Review 33 (2): 127–140. doi:10.1103/PhysRev.33.127. Bibcode: 1929PhRv...33..127G.
- ↑ Condon, E.U. (1978). "Tunneling – How It All Started". American Journal of Physics 46 (4): 319–323. doi:10.1119/1.11306. Bibcode: 1978AmJPh..46..319C.
- ↑ Mueller, E.W. (1937). "Elektronenmikroskopische Beobachtungen von Feldkathoden". Z. Phys. 106 (9–10): 541–550. doi:10.1007/BF01339895. Bibcode: 1937ZPhy..106..541M.
- ↑ Gomer, R. (1961). Field emission and field ionization. Cambridge, Massachusetts: Harvard Univ. Press. ISBN 1-56396-124-5.
- ↑ Swanson, L.W.; Bell, A.E. (1975). "Recent advances in field electron microscopy of metals". Advances in Electronics and Electron Physics 32: 193–309. doi:10.1016/S0065-2539(08)60236-X. ISBN 9780120145324.
- ↑ "The role of the adsorbed state in heterogeneous catalysis", Discuss. Faraday Soc., Vol. 41 (1966)
- ↑ 27.0 27.1 Dyke, W.P.; Trolan, J.K. (1953). "Field emission: Large current densities, space charge, and the vacuum arc". Physical Review 89 (4): 799–808. doi:10.1103/PhysRev.89.799. Bibcode: 1953PhRv...89..799D.
- ↑ Dyke, W.P.; Dolan, W.W. (1956). "Field emission". Advances in Electronics and Electron Physics 8: 89–185. doi:10.1016/S0065-2539(08)61226-3. ISBN 9780120145089. Bibcode: 1956AEEP....8...89D.
- ↑ Pandey, A D; Muller, Gunter; Reschke, Detlef; Singer, Xenia (2009). "Field emission from crystalline niobium". Physical Review Special Topics - Accelerators and Beams 12 (2): 023501. doi:10.1103/PhysRevSTAB.12.023501. Bibcode: 2009PhRvS..12b3501D.
- ↑ 30.0 30.1 30.2 Abbott, F. R.; Henderson, Joseph E. (1939). "The Range and Validity of the Field Current Equation". Physical Review 56 (1): 113–118. doi:10.1103/PhysRev.56.113. Bibcode: 1939PhRv...56..113A.
- ↑ 31.0 31.1 31.2 31.3 Young, Russell D. (1959). "Theoretical Total-Energy Distribution of Field-Emitted Electrons". Physical Review 113 (1): 110–114. doi:10.1103/PhysRev.113.110. Bibcode: 1959PhRv..113..110Y.
- ↑ Young, Russell D.; Müller, Erwin W. (1959). "Experimental Measurement of the Total-Energy Distribution of Field-Emitted Electrons". Physical Review 113 (1): 115–120. doi:10.1103/PhysRev.113.115. Bibcode: 1959PhRv..113..115Y.
- ↑ 33.0 33.1 33.2 33.3 33.4 33.5 33.6 A. Modinos (1984). Field, Thermionic and Secondary Electron Emission Spectroscopy. Plenum, New York. ISBN 0-306-41321-3.
- ↑ 34.0 34.1 34.2 34.3 34.4 Gadzuk, J. W.; Plummer, E. W. (1973). "Field Emission Energy Distribution (FEED)". Reviews of Modern Physics 45 (3): 487–548. doi:10.1103/RevModPhys.45.487. Bibcode: 1973RvMP...45..487G.
- ↑ Crewe, A. V.; Wall, J.; Langmore, J. (1970). "Visibility of Single Atoms". Science 168 (3937): 1338–40. doi:10.1126/science.168.3937.1338. PMID 17731040. Bibcode: 1970Sci...168.1338C.
- ↑ Charbonnier, F (1996). "Developing and using the field emitter as a high intensity electron source". Applied Surface Science 94-95: 26–43. doi:10.1016/0169-4332(95)00517-X. Bibcode: 1996ApSS...94...26C.
- ↑ 37.0 37.1 J.Orloff, ed (2008). Handbook of Charged Particle Optics (2 ed.). CRC Press.
- ↑ L.W. Swanson and A.E. Bell, Adv. Electron. Electron Phys. 32 (1973) 193
- ↑ Swanson, L. W. (1975). "Comparative study of the zirconiated and built-up W thermal-field cathode". Journal of Vacuum Science and Technology 12 (6): 1228. doi:10.1116/1.568503. Bibcode: 1975JVST...12.1228S.
- ↑ 40.0 40.1 40.2 40.3 Milne WI (Sep 2008). E nano newsletter. http://www.phantomsnet.net/Foundation/Enano_newsletter13.php.
- ↑ 41.0 41.1 De Jonge, Niels; Bonard, Jean-Marc (2004). "Carbon nanotube electron sources and applications". Philosophical Transactions of the Royal Society A 362 (1823): 2239–66. doi:10.1098/rsta.2004.1438. PMID 15370480. Bibcode: 2004RSPTA.362.2239D.
- ↑ 42.0 42.1 P.W. Hawkes; E. Kaspar (1996). "44,45". Principles of Electron Optics. 2. Academic Press, London.
- ↑ Dyke, W. P.; Trolan, J. K.; Dolan, W. W.; Barnes, George (1953). "The Field Emitter: Fabrication, Electron Microscopy, and Electric Field Calculations". Journal of Applied Physics 24 (5): 570. doi:10.1063/1.1721330. Bibcode: 1953JAP....24..570D.
- ↑ Everhart, T. E. (1967). "Simplified Analysis of Point-Cathode Electron Sources". Journal of Applied Physics 38 (13): 4944. doi:10.1063/1.1709260. Bibcode: 1967JAP....38.4944E.
- ↑ Wiesner, J. C. (1973). "Point-cathode electron sources-electron optics of the initial diode region". Journal of Applied Physics 44 (5): 2140. doi:10.1063/1.1662526. Bibcode: 1973JAP....44.2140W.
- ↑ Wiesner, J. C. (1974). "Point-cathode electron sources-Electron optics of the initial diode region: Errata and addendum". Journal of Applied Physics 45 (6): 2797. doi:10.1063/1.1663676. Bibcode: 1974JAP....45.2797W.
- ↑ 47.0 47.1 Fink, Hans-Werner (1988). "Point source for ions and electrons". Physica Scripta 38 (2): 260–263. doi:10.1088/0031-8949/38/2/029. Bibcode: 1988PhyS...38..260F.
- ↑ 48.0 48.1 Ward, B. W.; Notte, John A.; Economou, N. P. (2006). "Helium ion microscope: A new tool for nanoscale microscopy and metrology". Journal of Vacuum Science and Technology B 24 (6): 2871. doi:10.1116/1.2357967. Bibcode: 2006JVSTB..24.2871W.
- ↑ Binh, Vu Thien; Garcia, N.; Purcell, S.T. (1996). "Electron Field Emission from Atom-Sources: Fabrication, Properties, and Applications of Nanotips". Advances in Imaging and Electron Physics 95: 63–153. doi:10.1016/S1076-5670(08)70156-3. ISBN 9780120147373.
- ↑ 50.0 50.1 50.2 Spindt, C. A. (1976). "Physical properties of thin-film field emission cathodes with molybdenum cones". Journal of Applied Physics 47 (12): 5248–5263. doi:10.1063/1.322600. Bibcode: 1976JAP....47.5248S.
- ↑ 51.0 51.1 51.2 R.V. Latham, ed (1995). High-Voltage Vacuum Insulation: Basic Concepts and Technological Practice. Academic, London.
- ↑ Forbes, R (2001). "Low-macroscopic-field electron emission from carbon films and other electrically nanostructured heterogeneous materials: hypotheses about emission mechanism". Solid-State Electronics 45 (6): 779–808. doi:10.1016/S0038-1101(00)00208-2. Bibcode: 2001SSEle..45..779F.
- ↑ Robertson, J (2002). "Diamond-like amorphous carbon". Materials Science and Engineering: R: Reports 37 (4–6): 129–281. doi:10.1016/S0927-796X(02)00005-0.
- ↑ S.R.P. Silva; J.D. Carey; R.U.A. Khan; E.G. Gerstner; J.V. Anguita (2002). "9". in H.S. Nalwa. Handbook of Thin Film Materials. Academic, London.
- ↑ Hojati-Talemi, P.; Simon, G. (2011). "Field emission study of graphene nanowalls prepared by microwave-plasma method". Carbon 49 (8): 2875–2877. doi:10.1016/j.carbon.2011.03.004.
- ↑ Xu, N; Huq, S (2005). "Novel cold cathode materials and applications". Materials Science and Engineering: R: Reports 48 (2–5): 47–189. doi:10.1016/j.mser.2004.12.001.
- ↑ 57.0 57.1 Hojati-Talemi, Pejman; Hawkins, Stephen; Huynh, Chi; Simon, George P. (2013). "Understanding parameters affecting field emission properties of directly spinnable carbon nanotube webs". Carbon 57: 388–394. doi:10.1016/j.carbon.2013.01.088.
- ↑ 58.0 58.1 Hojati-Talemi, Pejman; Hawkins, Stephen C.; Huynh, Chi P.; Simon, George P. (2013). "Highly efficient low voltage electron emission from directly spinnable carbon nanotube webs". Carbon 57: 169–173. doi:10.1016/j.carbon.2013.01.060.
- ↑ Kuznetzov, Alexander A.; Lee, Sergey B.; Zhang, Mei; Baughman, Ray H.; Zakhidov, Anvar A. (2010). "Electron field emission from transparent multiwalled carbon nanotube sheets for inverted field emission displays". Carbon 48: 41–46. doi:10.1016/j.carbon.2009.08.009.
- ↑ 60.0 60.1 H. Craig Miller (November 2003). "Bibliography: electrical discharges in vacuum: 1877-2000". http://isdeiv.lbl.gov/MillerBiblio/WBib2000Txt.htm.
- ↑ Rhoderick, E. H. (1978). Metal-Semiconductor Contacts. Oxford: Clarendon Press. ISBN 0-19-859323-6.
- ↑ Forbes, R (1999). "The electrical surface as centroid of the surface-induced charge". Ultramicroscopy 79 (1–4): 25–34. doi:10.1016/S0304-3991(99)00098-4.
- ↑ 63.0 63.1 Herring, Conyers; Nichols, M. (1949). "Thermionic Emission". Reviews of Modern Physics 21 (2): 185–270. doi:10.1103/RevModPhys.21.185. Bibcode: 1949RvMP...21..185H.
- ↑ W. Schottky (1914). Phys. Z. 15: 872.
- ↑ 65.0 65.1 L.W. Nordheim (1928). "The Effect of the Image Force on the Emission and Reflexion of Electrons by Metals". Proceedings of the Royal Society A 121 (788): 626–639. doi:10.1098/rspa.1928.0222. Bibcode: 1928RSPSA.121..626N.
- ↑ H. Jeffreys (1924). "On Certain Approximate Solutions of Lineae Differential Equations of the Second Order". Proceedings of the London Mathematical Society 23: 428–436. doi:10.1112/plms/s2-23.1.428.
- ↑ 67.0 67.1 67.2 Forbes, Richard G. (2008). "On the need for a tunneling pre-factor in Fowler–Nordheim tunneling theory". Journal of Applied Physics 103 (11): 114911–114911–8. doi:10.1063/1.2937077. Bibcode: 2008JAP...103k4911F. http://epubs.surrey.ac.uk/22/1/fulltext.pdf.
- ↑ H. Fröman and P.O. Fröman, "JWKB approximation: contributions to the theory" (North-Holland, Amsterdam, 1965).
- ↑ 69.0 69.1 69.2 69.3 69.4 69.5 69.6 69.7 Forbes, Richard G.; Deane, Jonathan H.B. (2007). "Reformulation of the standard theory of Fowler–Nordheim tunnelling and cold field electron emission". Proceedings of the Royal Society A 463 (2087): 2907–2927. doi:10.1098/rspa.2007.0030. Bibcode: 2007RSPSA.463.2907F.
- ↑ Deane, Jonathan H B; Forbes, Richard G (2008). "The formal derivation of an exact series expansion for the principal Schottky–Nordheim barrier function, using the Gauss hypergeometric differential equation". Journal of Physics A: Mathematical and Theoretical 41 (39): 395301. doi:10.1088/1751-8113/41/39/395301. Bibcode: 2008JPhA...41M5301D.
- ↑ 71.0 71.1 Burgess, R. E.; Houston, J. M.; Houston, J. (1953). "Corrected Values of Fowler–Nordheim Field Emission Functions v(y) and s(y)". Physical Review 90 (4): 515. doi:10.1103/PhysRev.90.515. Bibcode: 1953PhRv...90..515B.
- ↑ 72.0 72.1 72.2 Murphy, E. L.; Good, R. H. (1956). "Thermionic Emission, Field Emission, and the Transition Region". Physical Review 102 (6): 1464–1473. doi:10.1103/PhysRev.102.1464. Bibcode: 1956PhRv..102.1464M.
- ↑ 73.0 73.1 73.2 73.3 Forbes, Richard G. (2004). "Use of energy-space diagrams in free-electron models of field electron emission". Surface and Interface Analysis 36 (56): 395–401. doi:10.1002/sia.1900.
- ↑ Gradshteyn and Rhyzhik (1980). Tables of Integrals, Series and Products. Academic, New York. see formula 3.241 (2), with μ=1
- ↑ 75.0 75.1 Modinos, A (2001). "Theoretical analysis of field emission data". Solid-State Electronics 45 (6): 809–816. doi:10.1016/S0038-1101(00)00218-5. Bibcode: 2001SSEle..45..809M.
- ↑ Forbes, Richard G. (2008). "Physics of generalized Fowler–Nordheim-type equations". Journal of Vacuum Science and Technology B 26 (2): 788. doi:10.1116/1.2827505. Bibcode: 2008JVSTB..26..788F.
- ↑ Forbes, Richard G. (2008). "Description of field emission current/voltage characteristics in terms of scaled barrier field values (f-values)". Journal of Vacuum Science and Technology B 26 (1): 209. doi:10.1116/1.2834563. Bibcode: 2008JVSTB..26..209F.
- ↑ L.W. Nordheim (1928). "Zur Theorie der thermischen Emission und der Reflexion von Elektronen an Metallen". Z. Phys. 46 (11–12): 833–855. doi:10.1007/BF01391020. Bibcode: 1928ZPhy...46..833N.
- ↑ Stratton, Robert (1962). "Theory of Field Emission from Semiconductors". Physical Review 125 (1): 67–82. doi:10.1103/PhysRev.125.67. Bibcode: 1962PhRv..125...67S.
- ↑ Forbes, Richard G. (2008). "Exact analysis of surface field reduction due to field-emitted vacuum space charge, in parallel-plane geometry, using simple dimensionless equations". Journal of Applied Physics 104 (8): 084303–084303–10. doi:10.1063/1.2996005. Bibcode: 2008JAP...104h4303F. http://epubs.surrey.ac.uk/307/1/fulltext.pdf.
- ↑ Forbes, R; Edgcombe, CJ; Valdrè, U (2003). "Some comments on models for field enhancement". Ultramicroscopy 95 (1–4): 57–65. doi:10.1016/S0304-3991(02)00297-8. PMID 12535545.
- ↑ Smith, R. C.; Forrest, R. D.; Carey, J. D.; Hsu, W. K.; Silva, S. R. P. (2005). "Interpretation of enhancement factor in nonplanar field emitters". Applied Physics Letters 87 (1): 013111. doi:10.1063/1.1989443. Bibcode: 2005ApPhL..87a3111S. http://epubs.surrey.ac.uk/153/1/fulltext.pdf.
- ↑ 83.0 83.1 83.2 Kyritsakis, A.; Xanthakis, J. P. (2015). "Derivation of a generalized Fowler–Nordheim equation for nanoscopic field-emitters". Proceedings of the Royal Society A 471 (2174): 20140811. doi:10.1098/rspa.2014.0811. Bibcode: 2015RSPSA.47140811K.
- ↑ He, J.; Cutler, P. H. (1991). "Derivation of a generalized Fowler–Nordheim equation for nanoscopic field-emitters". Applied Physics Letters 59 (13): 1644. doi:10.1063/1.106257. Bibcode: 1991ApPhL..59.1644H.
- ↑ Fursey, G. N.; Glazanov, D. V. (1998). "Deviations from the Fowler–Nordheim theory and peculiarities of field electron emission from small-scale objects". Journal of Vacuum Science and Technology B 16 (2): 910. doi:10.1116/1.589929. Bibcode: 1998JVSTB..16..910F.
- ↑ Cabrera, H. (2013). "Scale invariance of a diodelike tunnel junction". Physical Review B 87 (11): 115436. doi:10.1103/PhysRevB.87.115436. Bibcode: 2013PhRvB..87k5436C.
- ↑ Kyritsakis, Andreas (2023-03-21). "General form of the tunneling barrier for nanometrically sharp electron emitters". Journal of Applied Physics 133 (11): 113302. doi:10.1063/5.0144608. ISSN 0021-8979. Bibcode: 2023JAP...133k3302K. https://doi.org/10.1063/5.0144608.
- ↑ Kyritsakis, A.; Djurabekova, F. (2017). "A general computational method for electron emission and thermal effects in field emitting nanotips". Computational Materials Science 128: 15. doi:10.1016/j.commatsci.2016.11.010.
- ↑ Forbes, Richard G. (2008). "Call for experimental test of a revised mathematical form for empirical field emission current-voltage characteristics". Applied Physics Letters 92 (19): 193105. doi:10.1063/1.2918446. Bibcode: 2008ApPhL..92s3105F. http://epubs.surrey.ac.uk/391/1/fulltext.pdf.
- ↑ Jensen, K. L. (1999). "Exchange-correlation, dipole, and image charge potentials for electron sources: Temperature and field variation of the barrier height". Journal of Applied Physics 85 (5): 2667. doi:10.1063/1.369584. Bibcode: 1999JAP....85.2667J.
- ↑ T. Kirk, 21st Intern. Vacuum Nanoelectronics Conf., Wrocław, July 2008.
- ↑ Modinos, A (1974). "Field emission from surface states in semiconductors". Surface Science 42 (1): 205–227. doi:10.1016/0039-6028(74)90013-2. Bibcode: 1974SurSc..42..205M.
Further reading
- General information
- W. Zhu, ed (2001). Vacuum Microelectronics. Wiley, New York.
- G.N. Fursey (2005). Field Emission in Vacuum Microelectronics. Kluwer Academic, New York. ISBN 0-306-47450-6.
Field penetration and band bending (semiconductors)
- Seiwatz, Ruth; Green, Mino (1958). "Space Charge Calculations for Semiconductors". Journal of Applied Physics 29 (7): 1034. doi:10.1063/1.1723358. Bibcode: 1958JAP....29.1034S.
- A. Many, Y. Goldstein, and N.B. Grover, Semiconductor Surfaces (North Holland, Amsterdam, 1965).
- W. Mönsch, Semiconductor Surfaces and Interfaces (Springer, Berlin, 1995).
- Peng, Jie; Li, Zhibing; He, Chunshan; Chen, Guihua; Wang, Weiliang; Deng, Shaozhi; Xu, Ningsheng; Zheng, Xiao et al. (2008). "The roles of apex dipoles and field penetration in the physics of charged, field emitting, single-walled carbon nanotubes". Journal of Applied Physics (AIP Publishing) 104 (1): 014310–014310–12. doi:10.1063/1.2946449. ISSN 0021-8979. Bibcode: 2008JAP...104a4310P.
- Field emitted vacuum space-charge
- Barbour, J. P.; Dolan, W. W.; Trolan, J. K.; Martin, E. E.; Dyke, W. P. (1953). "Space-Charge Effects in Field Emission". Physical Review 92 (1): 45–51. doi:10.1103/PhysRev.92.45. Bibcode: 1953PhRv...92...45B.
- Field emission at high temperatures, and photo-field emission
- Jensen, Kevin (2007). Electron emission physics. Advances in Imaging and Electron Physics. 149. San Diego: Academic Press. ISBN 978-0-12-374207-0. OCLC 647688316.
- Field-induced explosive electron emission
- G.A. Mesyats, Explosive Electron Emission (URO Press, Ekaterinburg, 1998),
 |
