Physics:Neutron–proton ratio

Short description: Ratio of neutrons to protons in an atomic nucleus

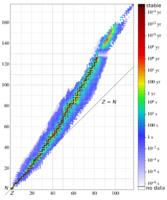
The neutron–proton ratio (N/Z ratio or nuclear ratio) of an atomic nucleus is the ratio of its number of neutrons to its number of protons. Among stable nuclei and naturally occurring nuclei, this ratio generally increases with increasing atomic number. This is because electrical repulsive forces between protons scale with distance differently than strong nuclear force attractions. In particular, most pairs of protons in large nuclei are not far enough apart, such that electrical repulsion dominates over the strong nuclear force, and thus proton density in stable larger nuclei must be lower than in stable smaller nuclei where more pairs of protons have appreciable short-range nuclear force attractions.

For many elements with atomic number Z small enough to occupy only the first three nuclear shells, that is up to that of calcium (Z = 20), there exists a stable isotope with N/Z ratio of one. The exceptions are beryllium (N/Z = 1.25) and every element with odd atomic number between 9 and 19 inclusive (though in those cases N = Z + 1 always allows for stability). Hydrogen-1 (N/Z ratio = 0) and helium-3 (N/Z ratio = 0.5) are the only stable isotopes with neutron–proton ratio under one. Uranium-238 has the highest N/Z ratio of any primordial nuclide at 1.587, while mercury-204 has the highest N/Z ratio of any known stable isotope at 1.55. Radioactive decay generally proceeds so as to change the N/Z ratio to increase stability. If the N/Z ratio is greater than 1, alpha decay increases the N/Z ratio, and hence provides a common pathway towards stability for decays involving large nuclei with too few neutrons. Positron emission and electron capture also increase the ratio, while beta decay decreases the ratio.

Nuclear waste exists mainly because nuclear fuel has a higher stable N/Z ratio than its fission products.

Semi-empirical description

For stable nuclei, the neutron-proton ratio is such that the binding energy is at a local minimum or close to a minimum.

From the liquid drop model, this bonding energy is approximated by empirical Bethe–Weizsäcker formula

[math]\displaystyle{ E_{B} = a_{V} A - a_{S} A^{2/3} - a_{C} \frac{Z^2}{A^{1/3}} - a_{A} \frac{(A - 2Z)^{2}}{A} \pm \delta(A,Z). }[/math]

Given a value of [math]\displaystyle{ A }[/math] and ignoring the contributions of nucleon spin pairing (i.e. ignoring the [math]\displaystyle{ \pm \delta(A,Z) }[/math] term), the binding energy is a quadratic expression in [math]\displaystyle{ Z }[/math] that is minimized when the neutron-proton ratio is [math]\displaystyle{ N/Z \approx 1 + \frac{a_C}{2a_A} A^{2/3} }[/math].

Isotope half-lives. Note that the plot for stable isotopes diverges from the line Z = N as the element number Z becomes larger

See also

• Isotope § Variation in properties between isotopes
• Nuclear fission
• Nuclear drip line