Physics:Valley of stability

From HandWiki
Short description: Characterization of nuclide stability
Nuclear physics
NuclearReaction.svg
Nucleus · Nucleons (p, n) · Nuclear matter · Nuclear force · Nuclear structure · Nuclear reaction
Models of the nucleus
Liquid drop · Nuclear shell model · Interacting boson model · Ab initio
Nuclides' classification
Stable · Magic · Even/odd · Halo (Borromean)
Nuclear stability
Binding energy · p–n ratio · Drip line · Island of stability · Valley of stability · Stable nuclide
Radioactive decay
Alpha α · Beta β (2β, β+) · K/L capture · Isomeric (Gamma γ · Internal conversion) · Spontaneous fission · Cluster decay · Neutron emission · Proton emission
Nuclear fission
Spontaneous · Products (pair breaking) · Photofission
Capturing processes
electron (2×) · neutron (s · r) · proton (p · rp)
High-energy processes
Spallation (by cosmic ray) · Photodisintegration
Nucleosynthesis and
nuclear astrophysics
Nuclear fusion
Processes: Stellar · Big Bang · Supernova
Nuclides: Primordial · Cosmogenic · Artificial
High-energy nuclear physics
Quark–gluon plasma · RHIC · LHC

In nuclear physics, the valley of stability (also called the belt of stability, nuclear valley, energy valley, or beta stability valley) is a characterization of the stability of nuclides to radioactivity based on their binding energy.[1] Nuclides are composed of protons and neutrons. The shape of the valley refers to the profile of binding energy as a function of the numbers of neutrons and protons, with the lowest part of the valley corresponding to the region of most stable nuclei.[2] The line of stable nuclides down the center of the valley of stability is known as the line of beta stability. The sides of the valley correspond to increasing instability to beta decay (β− or β+). The decay of a nuclide becomes more energetically favorable the further it is from the line of beta stability. The boundaries of the valley correspond to the nuclear drip lines, where nuclides become so unstable they emit single protons or single neutrons. Regions of instability within the valley at high atomic number also include radioactive decay by alpha radiation or spontaneous fission. The shape of the valley is roughly an elongated paraboloid corresponding to the nuclide binding energies as a function of neutron and atomic numbers.[1]

The nuclides within the valley of stability encompass the entire table of nuclides. The chart of those nuclides is also known as a Segrè chart, after the physicist Emilio Segrè.[3] The Segrè chart may be considered a map of the nuclear valley. The region of proton and neutron combinations outside of the valley of stability is referred to as the sea of instability.[4][5]

Scientists have long searched for long-lived heavy isotopes outside of the valley of stability,[6][7][8] hypothesized by Glenn T. Seaborg in the late 1960s.[9][10] These relatively stable nuclides are expected to have particular configurations of "magic" atomic and neutron numbers, and form a so-called island of stability.

Description

All atomic nuclei are composed of protons and neutrons bound together by the nuclear force. There are 286 primordial nuclides that occur naturally on earth, each corresponding to a unique number of protons, called the atomic number, Z, and a unique number of neutrons, called the neutron number, N. The mass number, A, of a nuclide is the sum of atomic and neutron numbers, A = Z + N. Not all nuclides are stable, however. According to Byrne,[3] stable nuclides are defined as those having a half-life greater than 1018 years, and there are many combinations of protons and neutrons that form nuclides that are unstable. A common example of an unstable nuclide is carbon-14 that decays by beta decay into nitrogen-14 with a half-life of about 5,730 years:

146C → 147N + e− + νe

In this form of decay, the original element becomes a new chemical element in a process known as nuclear transmutation and a beta particle and an electron antineutrino are emitted. An essential property of this and all nuclide decays is that the total energy of the decay product is less than that of the original nuclide. The difference between the initial and final nuclide binding energies is carried away by the kinetic energies of the decay products, often the beta particle and its associated neutrino.[3]

The concept of the valley of stability is a way of organizing all of the nuclides according to binding energy as a function of neutron and proton numbers.[1] Most stable nuclides have roughly equal numbers of protons and neutrons, so the line for which Z = N forms a rough initial line defining stable nuclides. The greater the number of protons, the more neutrons are required to stabilize a nuclide; nuclides with larger values for Z require an even larger number of neutrons, N > Z, to be stable. The valley of stability is formed by the negative of binding energy, the binding energy being the energy required to break apart the nuclide into its proton and neutron components. The stable nuclides have high binding energy, and these nuclides lie along the bottom of the valley of stability. Nuclides with weaker binding energy have combinations of N and Z that lie off of the line of stability and further up the sides of the valley of stability. Unstable nuclides can be formed in nuclear reactors or supernovas, for example. Such nuclides often decay in sequences of reactions called decay chains that take the resulting nuclides sequentially down the slopes of the valley of stability. The sequence of decays take nuclides toward greater binding energies, and the nuclides terminating the chain are stable.[1] The valley of stability provides both a conceptual approach for how to organize the myriad stable and unstable nuclides into a coherent picture and an intuitive way to understand how and why sequences of radioactive decay occur.[1]

  • Chart of nuclides (isotopes) by binding energy, depicting the valley of stability. The diagonal line corresponds to equal numbers of neutrons and protons. Dark blue squares represent nuclides with the greatest binding energy, hence they correspond to the most stable nuclides. The binding energy is greatest along the floor of the valley of stability.

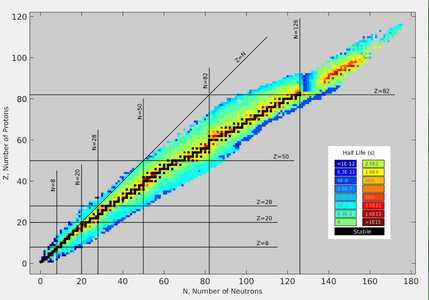
  • Chart of nuclides by half life. Black squares represent nuclides with the longest half lives hence they correspond to the most stable nuclides. The most stable, long-lived nuclides lie along the floor of the valley of stability. Nuclides with more than 20 protons must have more neutrons than protons to be stable.

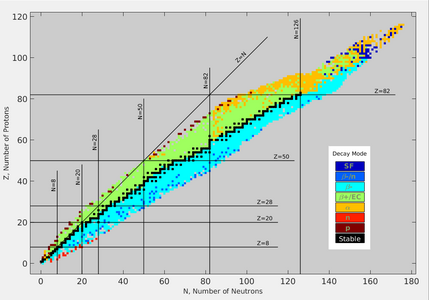
  • Chart of nuclides by type of decay. Black squares are stable nuclides. Nuclides with excessive neutrons or protons are unstable to β− (light blue) or β+ (green) decay, respectively. At high atomic number, alpha emission (orange) or spontaneous fission (dark blue) become common decay modes.

The role of neutrons

The protons and neutrons that comprise an atomic nucleus behave almost identically within the nucleus. The approximate symmetry of isospin treats these particles as identical, but in a different quantum state. This symmetry is only approximate, however, and the nuclear force that binds nucleons together is a complicated function depending on nucleon type, spin state, electric charge, momentum, etc. and with contributions from non-central forces. The nuclear force is not a fundamental force of nature, but a consequence of the residual effects of the strong force that surround the nucleons. One consequence of these complications is that although deuterium, a bound state of a proton (p) and a neutron (n) is stable, exotic nuclides such as diproton or dineutron are unbound.[11] The nuclear force is not sufficiently strong to form either p-p or n-n bound states, or equivalently, the nuclear force does not form a potential well deep enough to bind these identical nucleons.[citation needed]

Stable nuclides require approximately equal numbers of protons and neutrons. The stable nuclide carbon-12 (12C) is composed of six neutrons and six protons, for example. Protons have a positive charge, hence within a nuclide with many protons there are large repulsive forces between protons arising from the Coulomb force. By acting to separate protons from one another, the neutrons within a nuclide play an essential role in stabilizing nuclides. With increasing atomic number, even greater numbers of neutrons are required to obtain stability. The heaviest stable element, lead (Pb), has many more neutrons than protons. The stable nuclide 206Pb has Z = 82 and N = 124, for example. For this reason, the valley of stability does not follow the line Z = N for A larger than 40 (Z = 20 is the element calcium).[3] Neutron number increases along the line of beta stability at a faster rate than atomic number.

The line of beta stability follows a particular curve of neutron–proton ratio, corresponding to the most stable nuclides. On one side of the valley of stability, this ratio is small, corresponding to an excess of protons over neutrons in the nuclides. These nuclides tend to be unstable to β+ decay or electron capture, since such decay converts a proton to a neutron. The decay serves to move the nuclides toward a more stable neutron-proton ratio. On the other side of the valley of stability, this ratio is large, corresponding to an excess of neutrons over protons in the nuclides. These nuclides tend to be unstable to β− decay, since such decay converts neutrons to protons. On this side of the valley of stability, β− decay also serves to move nuclides toward a more stable neutron-proton ratio.

Neutrons, protons, and binding energy

The mass of an atomic nucleus is given by

[math]\displaystyle{ m = Z m_{p} + N m_{n} - \frac{E_{B}}{c^{2}} }[/math]

where [math]\displaystyle{ m_{p} }[/math] and [math]\displaystyle{ m_{n} }[/math] are the rest mass of a proton and a neutron, respectively, and [math]\displaystyle{ E_{B} }[/math] is the total binding energy of the nucleus. The mass–energy equivalence is used here. The binding energy is subtracted from the sum of the proton and neutron masses because the mass of the nucleus is less than that sum. This property, called the mass defect, is necessary for a stable nucleus; within a nucleus, the nuclides are trapped by a potential well. A semi-empirical mass formula states that the binding energy will take the form

[math]\displaystyle{ E_{B} = a_{V} A - a_{S} A^{2/3} - a_{C} \frac{Z^2}{A^{1/3}} - a_{A} \frac{(A - 2Z)^{2}}{A} \pm \delta(A,Z) }[/math][12]

The difference between the mass of a nucleus and the sum of the masses of the neutrons and protons that comprise it is known as the mass defect. EB is often divided by the mass number to obtain binding energy per nucleon for comparisons of binding energies between nuclides. Each of the terms in this formula has a theoretical basis. The coefficients [math]\displaystyle{ a_{V} }[/math], [math]\displaystyle{ a_{S} }[/math], [math]\displaystyle{ a_{C} }[/math], [math]\displaystyle{ a_{A} }[/math] and a coefficient that appears in the formula for [math]\displaystyle{ \delta(A,Z) }[/math] are determined empirically.

The binding energy expression gives a quantitative estimate for the neutron-proton ratio. The energy is a quadratic expression in Z that is minimized when the neutron-proton ratio is [math]\displaystyle{ N/Z \approx 1 + \frac{a_C}{2a_A} A^{2/3} }[/math]. This equation for the neutron-proton ratio shows that in stable nuclides the number of neutrons is greater than the number of protons by a factor that scales as [math]\displaystyle{ A^{2/3} }[/math].

The negative of binding energy per nucleon for the stable nuclides located along the bottom of the valley of stability. Iron-56 is about the most stable nuclide, and it is about the lowest point within the valley of stability.

The figure at right shows the average binding energy per nucleon as a function of atomic mass number along the line of beta stability, that is, along the bottom of the valley of stability. For very small atomic mass number (H, He, Li), binding energy per nucleon is small, and this energy increases rapidly with atomic mass number. Nickel-62 (28 protons, 34 neutrons) has the highest mean binding energy of all nuclides, while iron-58 (26 protons, 32 neutrons) and iron-56 (26 protons, 30 neutrons) are a close second and third.[13] These nuclides lie at the very bottom of the valley of stability. From this bottom, the average binding energy per nucleon slowly decreases with increasing atomic mass number. The heavy nuclide 238U is not stable, but is slow to decay with a half-life of 4.5 billion years.[1] It has relatively small binding energy per nucleon.

For β− decay, nuclear reactions have the generic form

AZX → AZ+1X′ + e− + νe[14]

where A and Z are the mass number and atomic number of the decaying nucleus, and X and X′ are the initial and final nuclides, respectively. For β+ decay, the generic form is

AZX → AZ−1X′ + e+ + νe[14]

These reactions correspond to the decay of a neutron to a proton, or the decay of a proton to a neutron, within the nucleus, respectively. These reactions begin on one side or the other of the valley of stability, and the directions of the reactions are to move the initial nuclides down the valley walls towards a region of greater stability, that is, toward greater binding energy.

The negative of binding energy per nucleon for nuclides with atomic mass number 125 plotted as a function of atomic number. The profile of binding energy across the valley of stability is roughly a parabola. Tellurium-125 (52Te) is stable, while antimony-125 (51Sb) is unstable to β− decay.

The figure at right shows the average binding energy per nucleon across the valley of stability for nuclides with mass number A = 125.[15] At the bottom of this curve is tellurium (52Te), which is stable. Nuclides to the left of 52Te are unstable with an excess of neutrons, while those on the right are unstable with an excess of protons. A nuclide on the left therefore undergoes β− decay, which converts a neutron to a proton, hence shifts the nuclide to the right and toward greater stability. A nuclide on the right similarly undergoes β+ decay, which shifts the nuclide to the left and toward greater stability.

Heavy nuclides are susceptible to α decay, and these nuclear reactions have the generic form,

AZX → A-4Z-2X′ + 42He

As in β decay, the decay product X′ has greater binding energy and it is closer to the middle of the valley of stability. The α particle carries away two neutrons and two protons, leaving a lighter nuclide. Since heavy nuclides have many more neutrons than protons, α decay increases a nuclide's neutron-proton ratio.

Proton and neutron drip lines

Main pages: Physics:Nuclear drip line, Physics:Proton emission, and Physics:Neutron emission

The boundaries of the valley of stability, that is, the upper limits of the valley walls, are the neutron drip line on the neutron-rich side, and the proton drip line on the proton-rich side. The nucleon drip lines are at the extremes of the neutron-proton ratio. At neutron–proton ratios beyond the drip lines, no nuclei can exist. The location of the neutron drip line is not well known for most of the Segrè chart, whereas the proton and alpha drip lines have been measured for a wide range of elements. Drip lines are defined for protons, neutrons, and alpha particles, and these all play important roles in nuclear physics.

The difference in binding energy between neighboring nuclides increases as the sides of the valley of stability are ascended, and correspondingly the nuclide half-lives decrease, as indicated in the figure above. If one were to add nucleons one at a time to a given nuclide, the process will eventually lead to a newly formed nuclide that is so unstable that it promptly decays by emitting a proton (or neutron). Colloquially speaking, the nucleon has 'leaked' or 'dripped' out of the nucleus, hence giving rise to the term "drip line".

Proton emission is not seen in naturally occurring nuclides. Proton emitters can be produced via nuclear reactions, usually utilizing linear particle accelerators (linac). Although prompt (i.e. not beta-delayed) proton emission was observed from an isomer in cobalt-53 as early as 1969, no other proton-emitting states were found until 1981, when the proton radioactive ground states of lutetium-151 and thulium-147 were observed at experiments at the GSI in West Germany.[16] Research in the field flourished after this breakthrough, and to date more than 25 nuclides have been found to exhibit proton emission. The study of proton emission has aided the understanding of nuclear deformation, masses and structure, and it is an example of quantum tunneling.

Two examples of nuclides that emit neutrons are beryllium-13 (mean life 2.7×10−21 s) and helium-5 (7×10−22 s). Since only a neutron is lost in this process, the atom does not gain or lose any protons, and so it does not become an atom of a different element. Instead, the atom will become a new isotope of the original element, such as beryllium-13 becoming beryllium-12 after emitting one of its neutrons.[17]

In nuclear engineering, a prompt neutron is a neutron immediately emitted by a nuclear fission event. Prompt neutrons emerge from the fission of an unstable fissionable or fissile heavy nucleus almost instantaneously. Delayed neutron decay can occur within the same context, emitted after beta decay of one of the fission products. Delayed neutron decay can occur at times from a few milliseconds to a few minutes.[18] The U.S. Nuclear Regulatory Commission defines a prompt neutron as a neutron emerging from fission within 10−14 seconds. [19]

Island of stability

Main page: Physics:Island of stability

The island of stability is a region outside the valley of stability where it is predicted that a set of heavy isotopes with near magic numbers of protons and neutrons will locally reverse the trend of decreasing stability in elements heavier than uranium. The hypothesis for the island of stability is based upon the nuclear shell model, which implies that the atomic nucleus is built up in "shells" in a manner similar to the structure of the much larger electron shells in atoms. In both cases, shells are just groups of quantum energy levels that are relatively close to each other. Energy levels from quantum states in two different shells will be separated by a relatively large energy gap. So when the number of neutrons and protons completely fills the energy levels of a given shell in the nucleus, the binding energy per nucleon will reach a local maximum and thus that particular configuration will have a longer lifetime than nearby isotopes that do not possess filled shells.[20]

A filled shell would have "magic numbers" of neutrons and protons. One possible magic number of neutrons for spherical nuclei is 184, and some possible matching proton numbers are 114, 120 and 126. These configurations imply that the most stable spherical isotopes would be flerovium-298, unbinilium-304 and unbihexium-310. Of particular note is 298Fl, which would be "doubly magic" (both its proton number of 114 and neutron number of 184 are thought to be magic). This doubly magic configuration is the most likely to have a very long half-life. The next lighter doubly magic spherical nucleus is lead-208, the heaviest known stable nucleus and most stable heavy metal.

Discussion

The valley of stability can be helpful in interpreting and understanding properties of nuclear decay processes such as decay chains and nuclear fission.

The uranium-238 series is a series of α (N and Z less 2) and β− decays (N less 1, Z plus 1) to nuclides that are successively deeper into the valley of stability. The series terminates at lead-206, a stable nuclide at the bottom of the valley of stability.

Radioactive decay often proceeds via a sequence of steps known as a decay chain. For example, 238U decays to 234Th which decays to 234mPa and so on, eventually reaching 206Pb:

[math]\displaystyle{ \begin{array}{l}{}\\ \ce{^{238}_{92}U-\gt [\alpha][4.5 \times 10^9 \ \ce y] {^{234}_{90}Th} -\gt [\beta^-][24 \ \ce d] {^{234\!m}_{91}Pa}} \ce{-\gt [\beta^-][1 \ \ce{min}]} \ce{^{234}_{92}U -\gt [\alpha][2.4 \times 10^5 \ \ce y] {^{230}_{90}Th} -\gt [\alpha][7.7 \times 10^4 \ \ce y] } \\ \ce{^{226}_{88}Ra -\gt [\alpha][1600 \ y] {^{222}_{86}Rn} -\gt [\alpha][3.8 \ \ce d] {^{218}_{84}Po} -\gt [\alpha][3 \ \ce{min}] {^{214}_{82}Pb} -\gt [\beta^-][27 \ \ce{min}] {^{214}_{83}Bi} -\gt [\beta^-][20 \ \ce{min}]} \\ \ce{^{214}_{84}Po -\gt [\alpha][164 \ \mu\ce{s}] {^{210}_{82}Pb} -\gt [\beta^-][22 \ \ce y] {^{210}_{83}Bi} -\gt [\beta^-][5 \ \ce d] {^{210}_{84}Po} -\gt [\alpha][138 \ \ce d] {^{206}_{82}Pb}}\\{} \end{array} }[/math]

With each step of this sequence of reactions, energy is released and the decay products move further down the valley of stability towards the line of beta stability. 206Pb is stable and lies on the line of beta stability.

Nuclear fission seen with a uranium-235 nucleus

The fission processes that occur within nuclear reactors are accompanied by the release of neutrons that sustain the chain reaction. Fission occurs when a heavy nuclide such as uranium-235 absorbs a neutron and breaks into nuclides of lighter elements such as barium or krypton, usually with the release of additional neutrons. Like all nuclides with a high atomic number, these uranium nuclei require many neutrons to bolster their stability, so they have a large neutron-proton ratio (N/Z). The nuclei resulting from a fission (fission products) inherit a similar N/Z, but have atomic numbers that are approximately half that of uranium.[1] Isotopes with the atomic number of the fission products and an N/Z near that of uranium or other fissionable nuclei have too many neutrons to be stable; this neutron excess is why multiple free neutrons but no free protons are usually emitted in the fission process, and it is also why many fission product nuclei undergo a long chain of β− decays, each of which converts a nucleus N/Z to (N − 1)/(Z + 1), where N and Z are, respectively, the numbers of neutrons and protons contained in the nucleus.

When fission reactions are sustained at a given rate, such as in a liquid-cooled or solid fuel nuclear reactor, the nuclear fuel in the system produces many antineutrinos for each fission that has occurred. These antineutrinos come from the decay of fission products that, as their nuclei progress down a β− decay chain toward the valley of stability, emit an antineutrino along with each β− particle. In 1956, Reines and Cowan exploited the (anticipated) intense flux of antineutrinos from a nuclear reactor in the design of an experiment to detect and confirm the existence of these elusive particles.[21]

See also


References

  1. ↑ 1.0 1.1 1.2 1.3 1.4 1.5 1.6 Mackintosh, R.; Ai-Khalili, J.; Jonson, B.; Pena, T. (2001) (in en-us). Nucleus: A trip into the heart of matter. Baltimore, Maryland: The Johns Hopkins University Press. pp. Chapter 6. ISBN 0-801 8-6860-2. https://archive.org/details/nucleustripintoh0000unse. 
  2. ↑ (in en) The valley of stability, https://www.youtube.com/watch?v=UTOp_2ZVZmM, retrieved 2023-12-01 
  3. ↑ 3.0 3.1 3.2 3.3 Byrne, J. (2011) (in en-us). Neutrons, Nuclei and Matter: An Exploration of the Physics of Slow Neutrons. Mineola, New York: Dover Publications. ISBN 978-0486482385. 
  4. ↑ Shaughnessy, D.. "Discovery of Elements 113 and 115". Lawrence Livermore National Laboratory. https://pls.llnl.gov/research-and-development/nuclear-science/project-highlights/livermorium/elements-113-and-115. 
  5. ↑ Seaborg, G. T.; Loveland, W.; Morrissey, D. J. (1979). "Superheavy elements: a crossroads". Science 203 (4382): 711–717. doi:10.1126/science.203.4382.711. PMID 17832968. Bibcode: 1979Sci...203..711S. https://escholarship.org/uc/item/6hg0t2d4. 
  6. ↑ Chowdhury, P. Roy; Samanta, C.; Basu, D. N. (2008). "Search for long lived heaviest nuclei beyond the valley of stability". Physical Review C 77 (4): 044603. doi:10.1103/PhysRevC.77.044603. Bibcode: 2008PhRvC..77d4603C. 
  7. ↑ Rare Isotope Science Assessment; Committee Board on Physics and Astronomy; Division on Engineering and Physical Sciences; National Research Council (2007). Scientific Opportunities with a Rare-Isotope Facility in the United States. National Academies Press. ISBN 9780309104081. https://books.google.com/books?id=y8uaAgAAQBAJ. 
  8. ↑ Boutin, C. (2002). "Climbing out of the nuclear valley". CERN Courier. http://cerncourier.com/cws/article/cern/28587. Retrieved 13 July 2016. 
  9. ↑ Seaborg, G. T. (1987). "Superheavy elements". Contemporary Physics 28: 33–48. doi:10.1080/00107518708211038. Bibcode: 1987ConPh..28...33S. 
  10. ↑ Sacks (2004). "Greetings From the Island of Stability". The New York Times. Archived from the original on 2023-10-13. https://web.archive.org/web/20231013105637/http://user.engineering.uiowa.edu/~emtheory/interesting_news/new%20elements.doc. 
  11. ↑ M. Schirber (2012). "Focus: Nuclei Emit Paired-up Neutrons". Physics 5: 30. doi:10.1103/physics.5.30. Bibcode: 2012PhyOJ...5...30S. 
  12. ↑ "Nuclear Masses and Binding Energy Lesson 3". http://oregonstate.edu/instruct/ch374/ch418518/lecture3-1.pdf. 
  13. ↑ Fewell, M. P. (1995). "The atomic nuclide with the highest mean binding energy". American Journal of Physics 63 (7): 653–58. doi:10.1119/1.17828. Bibcode: 1995AmJPh..63..653F. 
  14. ↑ 14.0 14.1 Konya, J.; Nagy, N. M. (2012). Nuclear and Radio-chemistry. Elsevier. pp. 74–75. ISBN 978-0-12-391487-3. 
  15. ↑ K. S. Krane (1988). Introductory Nuclear Physics. New York: John Wiley and Sons. 
  16. ↑ S. Hofmann (1996). Proton radioactivity, Ch. 3 of Nuclear Decay Modes, Ed. Dorin N. Poenaru. Institute of Physics Publishing, Bristol. pp. 143–203. ISBN 978-0-7503-0338-5. 
  17. ↑ "Neutron Emission" (webpage). http://education.jlab.org/glossary/neutron_emission.html. 
  18. ↑ DOE Fundamentals Handbook - Nuclear Physics and Reactor Theory, DOE-HDBK-1019/1-93, U.S. Department of Energy, January 1993, p. 29 (p. 133 of .pdf format), http://energy.gov/sites/prod/files/2013/06/f2/h1019v1.pdf, retrieved 2010-06-03 
  19. ↑ Mihalczo, John T. (November 19, 2004), Radiation Detection From Fission, ORNL/TM-2004/234, Oak Ridge National Laboratory, p. 1 (p. 11 of .pdf format), http://www.ornl.gov/~webworks/cppr/y2004/rpt/121589.pdf?origin=publication_detail 
  20. ↑ "Shell Model of Nucleus". HyperPhysics. Department of Physics and Astronomy, Georgia State University. http://hyperphysics.phy-astr.gsu.edu/hbase/nuclear/shell.html. 
  21. ↑ Reines, Frederick (December 8, 1995). "The Neutrino: From Poltergeist to Particle". Nobel Foundation. http://nobelprize.org/nobel_prizes/physics/laureates/1995/reines-lecture.pdf. "Nobel Prize lecture" 

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Physics:Valley_of_stability&oldid=3278366"