Physics:Standard illuminant

From HandWiki
Short description: Theoretical source of visible light
Relative spectral power distributions (SPDs) of CIE illuminants A, B, and C from 380 nm to 780 nm.

A standard illuminant is a theoretical source of visible light with a spectral power distribution that is published. Standard illuminants provide a basis for comparing images or colors recorded under different lighting.

CIE illuminants

The International Commission on Illumination (usually abbreviated CIE for its French name) is the body responsible for publishing all of the well-known standard illuminants. Each of these is known by a letter or by a letter-number combination.

Illuminants A, B, and C were introduced in 1931, with the intention of respectively representing average incandescent light, direct sunlight, and average daylight. Illuminants D (1967) represent variations of daylight, illuminant E is the equal-energy illuminant, while illuminants F (2004) represent fluorescent lamps of various composition.

There are instructions on how to experimentally produce light sources ("standard sources") corresponding to the older illuminants. For the relatively newer ones (such as series D), experimenters are left to measure to profiles of their sources and compare them to the published spectra:[1]

At present no artificial source is recommended to realize CIE standard illuminant D65 or any other illuminant D of different CCT. It is hoped that new developments in light sources and filters will eventually offer sufficient basis for a CIE recommendation.
—CIE, Technical Report (2004) Colorimetry, 3rd ed., Publication 15:2004, CIE Central Bureau, Vienna

Nevertheless, they do provide a measure, called the metamerism index, to assess the quality of daylight simulators.[2][3] The Metamerism Index tests how well five sets of metameric samples match under the test and reference illuminant. In a manner similar to the color rendering index, the average difference between the metamers is calculated.[4]

Illuminant A

The CIE defines illuminant A in these terms:

CIE standard illuminant A is intended to represent typical, domestic, tungsten-filament lighting. Its relative spectral power distribution is that of a Planckian radiator at a temperature of approximately 2856 K. CIE standard illuminant A should be used in all applications of colorimetry involving the use of incandescent lighting, unless there are specific reasons for using a different illuminant.
—CIE, CIE Standard Illuminants for Colorimetry

The spectral radiant exitance of a black body follows Planck's law:

[math]\displaystyle{ M_{e,\lambda}(\lambda, T) = \frac{c_1 \lambda^{-5}}{\exp\left(\frac{c_2}{\lambda T}\right) - 1}. }[/math]

At the time of standardizing illuminant A, both [math]\displaystyle{ c_1=2\pi \cdot h \cdot c^2 }[/math] (which does not affect the relative SPD) and [math]\displaystyle{ c_2=h \cdot c/k }[/math] were different. In 1968, the estimate of c2 was revised from 0.01438 m·K to 0.014388 m·K (and before that, it was 0.01435 m·K when illuminant A was standardized). This difference shifted the Planckian locus, changing the color temperature of the illuminant from its nominal 2848 K to 2856 K:

[math]\displaystyle{ T_{new} = T_{old} \times \frac{1.4388}{1.435} = 2848\ \text{K} \times 1.002648 = 2855.54\ \text{K}. }[/math]

In order to avoid further possible changes in the color temperature, the CIE now specifies the SPD directly, based on the original (1931) value of c2:[1]

[math]\displaystyle{ S_{A}(\lambda) = 100\left(\frac{560}{\lambda}\right)^5 \frac{\exp \frac{1.435 \times 10^7}{2848 \times 560} - 1}{\exp\frac{1.435 \times 10^7}{2848 \lambda} - 1}. }[/math]

The coefficients have been selected to achieve a normalized SPD of 100 at 560 nm. The tristimulus values are (X, Y, Z) = (109.85, 100.00, 35.58), and the chromaticity coordinates using the standard observer are (x, y) = (0.44758, 0.40745).

Illuminants B and C

Illuminants B and C are easily achieved daylight simulations. They modify illuminant A by using liquid filters. B served as a representative of noon sunlight, with a correlated color temperature (CCT) of 4874 K, while C represented average day light with a CCT of 6774 K. Unfortunately, they are poor approximations of any phase of natural daylight, particularly in the short-wave visible and in the ultraviolet spectral ranges. Once more realistic simulations were achievable, illuminants B and C were deprecated in favor of the D series.[1]

Illuminant C does not have the status of CIE standard illuminants but its relative spectral power distribution, tristimulus values and chromaticity coordinates are given in Table T.1 and Table T.3, as many practical measurement instruments and calculations still use this illuminant.
—CIE, Publication 15:2004[5]

Illuminant B was not so honored in 2004.

The liquid filters, designed by Raymond Davis, Jr. and Kasson S. Gibson in 1931,[6] have a relatively high absorbance at the red end of the spectrum, effectively increasing the CCT of the incandescent lamp to daylight levels. This is similar in function to a CTB color gel that photographers and cinematographers use today, albeit much less convenient.

Each filter uses a pair of solutions, comprising specific amounts of distilled water, copper sulfate, mannite, pyridine, sulfuric acid, cobalt, and ammonium sulfate. The solutions are separated by a sheet of uncolored glass. The amounts of the ingredients are carefully chosen so that their combination yields a color temperature conversion filter; that is, the filtered light is still white.

Illuminant series D

See also: CIE Standard Illuminant D65|Illuminant D65|CIE Standard Illuminant D65

Relative spectral power distribution of illuminant D and a black body of the same correlated color temperature (in red), normalized about 560 nm.

Derived by Judd, MacAdam, and Wyszecki,[7] the D series of illuminants are constructed to represent natural daylight. They are difficult to produce artificially, but are easy to characterize mathematically.

H. W. Budde of the National Research Council of Canada in Ottawa, H. R. Condit and F. Grum of the Eastman Kodak Company in Rochester, New York,[8] and S. T. Henderson and D. Hodgkiss of Thorn Electrical Industries in Enfield[9] had independently measured the spectral power distribution (SPD) of daylight from 330 nm to 700 nm, totaling among them 622 samples. Judd et al. analyzed these samples and found that the (x, y) chromaticity coordinates had a simple, quadratic relation:

[math]\displaystyle{ y = 2.870 x - 3.000 x^2 - 0.275. }[/math]

Simonds supervised the characteristic vector analysis of the SPDs.[10][11] Application of his method revealed that the SPDs could be satisfactorily approximated by using the mean (S0) and first two characteristic vectors (S1 and S2):

[math]\displaystyle{ S(\lambda) = S_0(\lambda) + M_1 S_1(\lambda) + M_2 S_2(\lambda). }[/math]

In simpler terms, the SPD of the studied daylight samples can be expressed as the linear combination of three, fixed SPDs. The first vector (S0) is the mean of all the SPD samples, which is the best reconstituted SPD that can be formed with only a fixed vector. The second vector (S1) corresponds to yellow–blue variation, accounting for changes in the correlated color temperature due to presence or absence of clouds or direct sunlight.[7] The third vector (S2) corresponds to pink–green variation caused by the presence of water in the form of vapor and haze.[7]

To construct a daylight simulator of a particular correlated color temperature one merely needs to know the coefficients M1 and M2 of the characteristic vectors S1 and S2.

Characteristic vectors of illuminant D; component SPDs S0 (blue), S1 (green), S2 (red).

Expressing the chromaticities x and y as:

[math]\displaystyle{ x = \frac{X_0 + M_1 X_1 + M_2 X_2}{S_0 + M_1 S_1 + M_2 S_2}, }[/math]
[math]\displaystyle{ y = \frac{Y_0 + M_1 Y_1 + M_2 Y_2}{S_0 + M_1 S_1 + M_2 S_2} }[/math]

and making use of known tristimulus values for the mean vectors, they were able to express M1 and M2 as follows:

Kelly's figures depicted the lines of constant correlated color temperature in uv space on the CIE 1960 UCS, as shown here, as well as on the familiar xy diagram.
[math]\displaystyle{ M_1 = \frac{-1.3515 - 1.7703 x + 5.9114 y}{0.0241 + 0.2562 x - 0.7341 y}, }[/math]
[math]\displaystyle{ M_2 = \frac{0.0300 - 31.4424 x + 30.0717 y}{0.0241 + 0.2562 x - 0.7341 y}. }[/math]

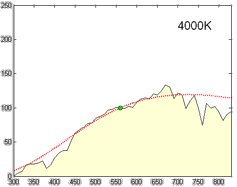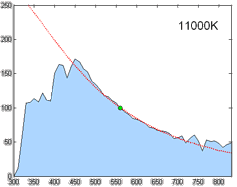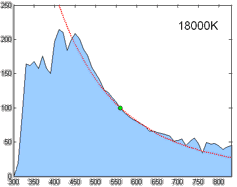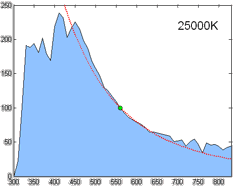
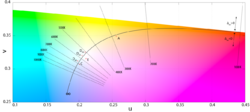
The only problem is that this left unsolved the computation of the coordinate [math]\displaystyle{ (x,y) }[/math] for a particular phase of daylight. Judd et al. simply tabulated the values of certain chromaticity coordinates, corresponding to commonly used correlated color temperatures, such as 5500 K, 6500 K, and 7500 K. For other color temperatures, one could consult figures made by Kelly.[12] This problem was addressed in the CIE report that formalized illuminant D, with an approximation of the x coordinate in terms of the reciprocal color temperature, valid from 4000 K to 25000 K.[13] The y coordinate trivially followed from Judd's quadratic relation.

Judd et al. then extended the reconstituted SPDs to 300 nm–330 nm and 700 nm–830 nm by using Moon's spectral absorbance data of the Earth's atmosphere.[14]

The tabulated SPDs presented by the CIE today are derived by linear interpolation of the 10 nm data set down to 5 nm.[15]

Similar studies have been undertaken in other parts of the world, or repeating Judd et al.'s analysis with modern computational methods. In several of these studies, the daylight locus is notably closer to the Planckian locus than in Judd et al.[16] [17]

Daylight locus in the CIE 1960 UCS. The isotherms are perpendicular to the Planckian locus. The two sections of the daylight locus, from 4000–7000 K and 7000–25000 K, are color-coded. Note that the two loci are separated by a fairly even distance, of around [math]\displaystyle{ \Delta_{uv}=0.003 }[/math].

Computation

The relative spectral power distribution (SPD) [math]\displaystyle{ S_D (\lambda) }[/math] of a D series illuminant can be derived from its chromaticity coordinates in the CIE 1931 color space, [math]\displaystyle{ (x_D,y_D) }[/math]:[18]

[math]\displaystyle{ x_D = \begin{cases} 0.244063 + 0.09911 \frac{10^3}{T} + 2.9678 \frac{10^6}{T^2} - 4.6070 \frac{10^9}{T^3} & 4000\ \mathrm{K} \leq T \leq 7000\ \ \mathrm{K} \\ 0.237040 + 0.24748 \frac{10^3}{T} + 1.9018 \frac{10^6}{T^2} - 2.0064 \frac{10^9}{T^3} & 7000\ \mathrm{K} \lt T \leq 25000\ \mathrm{K} \end{cases} }[/math]
[math]\displaystyle{ y_D = -3.000 x_D^2 + 2.870 x_D - 0.275 }[/math]

where T is the illuminant's CCT. The chromaticity coordinates of the illuminants D are said to form the CIE daylight locus. The relative SPD is given by:

[math]\displaystyle{ S_D(\lambda) = S_0(\lambda) + M_1 S_1(\lambda) + M_2 S_2(\lambda), }[/math]
[math]\displaystyle{ M_1 = (-1.3515 - 1.7703 x_D + 5.9114 y_D)/M, }[/math]
[math]\displaystyle{ M_2 = (0.0300 - 31.4424 x_D + 30.0717 y_D)/M, }[/math]
[math]\displaystyle{ M = 0.0241 + 0.2562 x_D - 0.7341 y_D }[/math]

where [math]\displaystyle{ S_0(\lambda), S_1(\lambda), S_2(\lambda) }[/math] are the mean and first two eigenvector SPDs, depicted above.[18] The characteristic vectors both have a zero at 560 nm, since all the relative SPDs have been normalized about this point.

The CCTs of the canonical illuminants, D50, D55, D65, and D75, differ slightly from what their names suggest. For example, D50 has a CCT of 5003 K ("horizon" light), while D65 has a CCT of 6504 K (noon light). As explained in a previous section, this is because the value of the constants in Planck's law have been slightly changed since the definition of these canonical illuminants, whose SPDs are based on the original values in Planck's law. In order to match all significant digits of the published data of the canonical illuminants the values of M1 and M2 have to be rounded to three decimal places before calculation of SD.[1]

Daylight simulator

Lighting cabinets, such as the Spectralight III, that use filtered incandescent lamps have better fits to the D illuminants in the 400 nm to 700 nm range than do the fluorescent daylight simulators (as of 1970).[19]

LED phosphor mixes are available to emulate the A, D, and E illuminants.[20]

Illuminant E

Illuminant E is beneath the Planckian locus, and roughly at the CCT of D55.

Illuminant E is an equal-energy radiator; it has a constant SPD inside the visible spectrum. It is useful as a theoretical reference; an illuminant that gives equal weight to all wavelengths. It also has equal CIE XYZ tristimulus values, thus its chromaticity coordinates are (x,y)=(1/3,1/3). This is by design; the XYZ color matching functions are normalized such that their integrals over the visible spectrum are the same.[1]

Illuminant E is not a black body, so it does not have a color temperature, but it can be approximated by a D series illuminant with a CCT of 5455 K. (Of the canonical illuminants, D55 is the closest.) Manufacturers sometimes compare light sources against illuminant E to calculate the excitation purity.[21]

Illuminant series F

The F series of illuminants represent various types of fluorescent lighting.

F1–F6 "standard" fluorescent lamps consist of two semi-broadband emissions of antimony and manganese activations in calcium halophosphate phosphor.[22] F4 is of particular interest since it was used for calibrating the CIE color rendering index (the CRI formula was chosen such that F4 would have a CRI of 51). F7–F9 are "broadband" (full-spectrum light) fluorescent lamps with multiple phosphors, and higher CRIs. Finally, F10–F12 are narrow triband illuminants consisting of three "narrowband" emissions (caused by ternary compositions of rare-earth phosphors) in the R,G,B regions of the visible spectrum. The phosphor weights can be tuned to achieve the desired CCT.

The spectra of these illuminants are published in Publication 15:2004.[5][23]

  • FL 1–6: Standard

  • FL 7–9: Broadband

  • FL 10–12: Narrowband

Illuminant series LED

Publication 15:2018 introduces new illuminants for different white LED types with CCTs ranging from approx. 2700 K to 6600 K.

LED-B1 through B5 defines LEDs with phosphor-converted blue light. LED-BH1 defines a blend of phosphor-converted blue and a red LED. LED-RGB1 defines the white light produced by a tricolor LED mix. LED-V1 and V2 define LEDs with phosphor-converted violet light.

White point

The spectrum of a standard illuminant, like any other profile of light, can be converted into tristimulus values. The set of three tristimulus coordinates of an illuminant is called a white point. If the profile is normalized, then the white point can equivalently be expressed as a pair of chromaticity coordinates.

If an image is recorded in tristimulus coordinates (or in values which can be converted to and from them), then the white point of the illuminant used gives the maximum value of the tristimulus coordinates that will be recorded at any point in the image, in the absence of fluorescence. It is called the white point of the image.

The process of calculating the white point discards a great deal of information about the profile of the illuminant, and so although it is true that for every illuminant the exact white point can be calculated, it is not the case that knowing the white point of an image alone tells you a great deal about the illuminant that was used to record it.

White points of standard illuminants

References

  1. ↑ 1.0 1.1 1.2 1.3 1.4 Schanda, János (2007). "3: CIE Colorimetry". Colorimetry: Understanding the CIE System. Wiley Interscience. pp. 37–46. ISBN 978-0-470-04904-4. 
  2. ↑ CIE Technical Report (1999). A Method for Assessing the Quality of Daylight Simulators for Colorimetry. 51.2-1999 (including Supplement 1-1999). Paris: Bureau central de la CIE. ISBN 978-92-9034-051-5. http://www.cie.co.at/publ/abst/51-2-99.html. "A method is provided for evaluating the suitability of a test source as a simulator of CIE Standard Illuminants D55, D65, or D75. The Supplement, prepared in 1999, adds the CIE Illuminant D50 to the line of illuminants where the method can be applied to. For each of these standard illuminants, spectral radiance factor data are supplied for five pairs of nonfluorescent samples that are metameric matches. The colorimetric differences of the five pairs are computed for the test illuminant; the average of these differences is taken as the visible range metamerism index and is used as a measure of the quality of the test illuminant as a simulator for nonfluorescent samples. For fluorescent samples, the quality is further assessed in terms of an ultraviolet range metamerism index, defined as the average of the colorimetric differences computed with the test illuminant for three further pairs of samples, each pair consisting of a fluorescent and a nonfluorescent sample which are metameric under the standard illuminant." 
  3. ↑ CIE Standard (2004). Standard Method of Assessing the Spectral Quality of Daylight Simulators for Visual Appraisal and Measurement of Colour. S012/E:2004. http://www.cie.co.at/publ/abst/s012.html.  Prepared by TC 1-53 "A Standard Method for Assessing the Quality of Daylight Simulators". ISO Standard 23603:2005(E).
  4. ↑ Lam, Yuk-Ming; Xin, John H. (August 2002). "Evaluation of the quality of different D65 simulators for visual assessment". Color Research & Application 27 (4): 243–251. doi:10.1002/col.10061. 
  5. ↑ 5.0 5.1 CIE Technical Report (2004). Colorimetry. Publication 15:2004 (3rd ed.). CIE Central Bureau, Vienna. ISBN 978-3-901906-33-6. http://www.cie.co.at/publ/abst/15-2004.html. 
  6. ↑ Davis, Raymond; Gibson, Kasson S. (January 21, 1931). "Filters for the reproduction of sunlight and daylight and the determination of color temperature". Precision Measurement and Calibration (National Bureau of Standards) 10: 641–805. 
  7. ↑ 7.0 7.1 7.2 Judd, Deane B.; MacAdam, David L.; Wyszecki, Günter (August 1964). "Spectral Distribution of Typical Daylight as a Function of Correlated Color Temperature". JOSA 54 (8): 1031–1040. doi:10.1364/JOSA.54.001031. 
  8. ↑ Condit, Harold R.; Grum, Frank (July 1964). "Spectral energy distribution of daylight". JOSA 54 (7): 937–944. doi:10.1364/JOSA.54.000937. 
  9. ↑ Henderson, Stanley Thomas; Hodgkiss, D. (1963). "The spectral energy distribution of daylight". British Journal of Applied Physics 14 (3): 125–131. doi:10.1088/0508-3443/14/3/307. 
    Henderson, Stanley Thomas; Hodgkiss, D. (1964). "The spectral energy distribution of daylight". British Journal of Applied Physics 15 (8): 947–952. doi:10.1088/0508-3443/15/8/310. 
  10. ↑ Simonds, John L. (August 1963). "Application of Characteristic Vector Analysis to Photographic and Optical Response Data". JOSA 53 (8): 968–974. doi:10.1364/JOSA.53.000968. 
  11. ↑ Tzeng, Di-Yuan; Berns, Roy S. (April 2005). "A review of principal component analysis and its applications to color technology". Color Research & Application 30 (2): 84–98. doi:10.1002/col.20086. 
  12. ↑ Kelly, Kenneth L. (August 1963). "Lines of Constant Correlated Color Temperature Based on MacAdam's (u,v) Uniform Chromaticity Transformation of the CIE Diagram". JOSA 53 (8): 999–1002. doi:10.1364/JOSA.53.000999. 
  13. ↑ Commission Internationale de l'Eclairage (1964). "Proceedings of the 15th Session, Vienna". 
  14. ↑ Moon, Parry (November 1940). "Proposed standard solar-radiation curves for engineering use". Journal of the Franklin Institute 230 (5): 583–617. doi:10.1016/S0016-0032(40)90364-7. 
  15. ↑ CIE 1931 and 1964 Standard Colorimetric Observers from 380 nm to 780 nm in increments of 5 nm.
  16. ↑ Studies from the 1960s and 1970s include:
    • G. T. Winch; M. C. Boshoff; C. J. Kok; A. G. du Toit (April 1966). "Spectroradiometric and Colorimetric Characteristics of Daylight in the Southern Hemisphere: Pretoria, South Africa". JOSA 56 (4): 456–464. doi:10.1364/JOSA.56.000456. "The derived chromaticities were found to be much closer to the full radiator locus than those previously published, which had been obtained in the northern hemisphere.". 
    • Das, S.R.; Sastri, V.D.P. (March 1965). "Spectral Distribution and Color of Tropical Daylight". JOSA 55 (3): 319–323. doi:10.1364/JOSA.55.000319. 
    • Sastri, V.D.P.; Das, S.R. (March 1968). "Typical Spectral Distributions and Color for Tropical Daylight". JOSA 58 (3): 391–398. doi:10.1364/JOSA.58.000391. 
    • Sastri, V.D.P. (January 11, 1976). "Locus of daylight chromaticities in relation to atmospheric conditions". Journal of Physics D: Applied Physics 9 (1): L1–L3. doi:10.1088/0022-3727/9/1/001. 
    • Dixon, E.R. (April 1978). "Spectral distribution of Australian daylight". JOSA 68 (4): 437–450. doi:10.1364/JOSA.68.000437. 
  17. ↑ Analyses using the faster computation of the 1990s and 2000s include:
  18. ↑ 18.0 18.1 The coefficients differ from those in the original paper due to the change in the constants in Planck's law. See Lindbloom for the current version, and Planckian locus for details.
  19. ↑ Wyszecki, Gunter (1970). "Development of New CIE Sources for Colorimetry". Die Farbe 19: 43–. 
  20. ↑ "CIE Illuminant Technology - Yujileds" (in en). 5 September 2023. https://www.yujiintl.com/cie-illuminant-technology/. 
  21. ↑ Philips. "Optical Testing for SuperFlux, SnapLED and LUXEON Emitters". http://www.philipslumileds.com/pdfs/AB08.pdf. "CIE has defined the color coordinates of several different white Illuminants, but within Lumileds, CIE illuminant E is used for all color calculations" 
  22. ↑ For commercial examples of calcium halophosphate fluorescents, see for example US patent 5447660 Method for making a calcium halophosphate phosphor or US patent 6666993 Single component calcium halophosphate phosphor
  23. ↑ Spectral power distribution of Illuminants Series F (Excel), in 5 nm increments from 380 nm to 780 nm.

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Physics:Standard_illuminant&oldid=3284517"