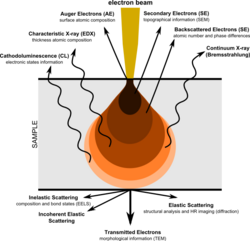
Physics:Electron backscatter diffraction

Short description: Scanning electron microscopy technique

An electron backscatter diffraction pattern of monocrystalline silicon, taken at 20 kV with a field-emission electron source

Electron backscatter diffraction (EBSD) is a scanning electron microscopy (SEM) technique used to study the crystallographic structure of materials. EBSD is carried out in a scanning electron microscope equipped with an EBSD detector comprising at least a phosphorescent screen, a compact lens and a low-light camera. In the microscope an incident beam of electrons hits a tilted sample. As backscattered electrons leave the sample, they interact with the atoms and are both elastically diffracted and lose energy, leaving the sample at various scattering angles before reaching the phosphor screen forming Kikuchi patterns (EBSPs). The EBSD spatial resolution depends on many factors, including the nature of the material under study and the sample preparation. They can be indexed to provide information about the material's grain structure, grain orientation, and phase at the micro-scale. EBSD is used for impurities and defect studies, plastic deformation, and statistical analysis for average misorientation, grain size, and crystallographic texture. EBSD can also be combined with energy-dispersive X-ray spectroscopy (EDS), cathodoluminescence (CL), and wavelength-dispersive X-ray spectroscopy (WDS) for advanced phase identification and materials discovery.

The change and sharpness of the electron backscatter patterns (EBSPs) provide information about lattice distortion in the diffracting volume. Pattern sharpness can be used to assess the level of plasticity. Changes in the EBSP zone axis position can be used to measure the residual stress and small lattice rotations. EBSD can also provide information about the density of geometrically necessary dislocations (GNDs). However, the lattice distortion is measured relative to a reference pattern (EBSP₀). The choice of reference pattern affects the measurement precision; e.g., a reference pattern deformed in tension will directly reduce the tensile strain magnitude derived from a high-resolution map while indirectly influencing the magnitude of other components and the spatial distribution of strain. Furthermore, the choice of EBSP₀ slightly affects the GND density distribution and magnitude.

Pattern formation and collection

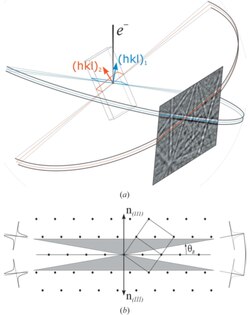
Setup geometry and pattern formation

Further information: Physics:Electron diffraction and Physics:Kikuchi lines

EBSD typical hardware configuration inside a field emission gun scanning electron microscope

For electron backscattering diffraction microscopy, a flat polished crystalline specimen is usually placed inside the microscope chamber. The sample is tilted at ~70° from Scanning electron microscope (SEM) flat specimen positioning and 110° to the electron backscatter diffraction (EBSD) detector. Tilting the sample elongates the interaction volume perpendicular to the tilt axis, allowing more electrons to leave the sample providing better signal. A high-energy electron beam (typically 20 kV) is focused on a small volume and scatters with a spatial resolution of ~20 nm at the specimen surface. The spatial resolution varies with the beam energy, angular width, interaction volume, nature of the material under study, and, in transmission Kikuchi diffraction (TKD), with the specimen thickness; thus, increasing the beam energy increases the interaction volume and decreases the spatial resolution.

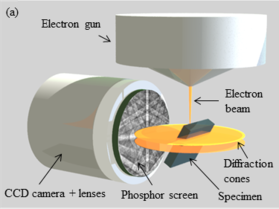
The EBSD detector is located within the specimen chamber of the SEM at an angle of approximately 90° to the pole piece. The EBSD detector is typically a phosphor screen that is excited by the backscattered electrons. The screen is coupled to lens which focuses the image from the phosphor screen onto a charge-coupled device (CCD) or complementary metal–oxide–semiconductor (CMOS) camera.

In this configuration, as the backscattered electrons leave the sample, they interact with the Coulomb potential and also lose energy due to inelastic scattering leading to a range of scattering angles (θ_hkl). The backscattered electrons form Kikuchi lines – having different intensities – on an electron-sensitive flat film/screen (commonly phosphor), gathered to form a Kikuchi band. These Kikuchi lines are the trace of a hyperbola formed by the intersection of Kossel cones with the plane of the phosphor screen. The width of a Kikuchi band is related to the scattering angles and, thus, to the distance d_hkl between lattice planes with Miller indexes h, k, and l. These Kikuchi lines and patterns were named after Seishi Kikuchi, who, together with Shoji Nishikawa, was the first to notice this diffraction pattern in 1928 using transmission electron microscopy (TEM) which is similar in geometry to X-ray Kossel pattern.

The systematically arranged Kikuchi bands, which have a range of intensity along their width, intersect around the centre of the regions of interest (ROI), describing the probed volume crystallography. These bands and their intersections form what is known as Kikuchi patterns or electron backscatter patterns (EBSPs). To improve contrast, the patterns’ background is corrected by removing anisotropic/inelastic scattering using static background correction or dynamic background correction.

Single-crystal 4H-SiC, gnomically projected EBSP collected using (left) conventional, (centre) dynamic, and (right) combined background correction

EBSD detectors

EBSD is conducted using an SEM equipped with an EBSD detector containing at least a phosphor screen, compact lens and low-light Charge-coupled device (CCD) or Complementary metal–oxide–semiconductor (CMOS) camera. (As of September 2023), commercially available EBSD systems typically come with one of two different CCD cameras: for fast measurements, the CCD chip has a native resolution of 640×480 pixels; for slower, and more sensitive measurements, the CCD chip resolution can go up to 1600×1200 pixels.

The biggest advantage of the high-resolution detectors is their higher sensitivity, and therefore the information within each diffraction pattern can be analysed in more detail. For texture and orientation measurements, the diffraction patterns are binned to reduce their size and computational times. Modern CCD-based EBSD systems can index patterns at a speed of up to 1800 patterns/second. This enables rapid and rich microstructural maps to be generated.

Sample preparation

Pattern degradation due to carbon deposition in a highly magnified location after 3-hour EBSPs acquisition around a deformation twin in the ferrite phase of duplex stainless steel

The sample should be vacuum stable. It is typically mounted using a conductive compound (e.g. an epoxy thermoset filled with Cu), which minimises image drift and sample charging under electron beam irradiation. EBSP quality is sensitive to surface preparation. Typically the sample is ground using SiC papers from 240 down to 4000 grit, and polished using diamond paste (from 9 to 1 µm) then in 50 nm colloidal silica. Afterwards, it is cleaned in ethanol, rinsed with deionised water, and dried with a hot air blower. This may be followed by ion beam polishing, for final surface preparation.

Inside the SEM, the size of the measurement area determines local resolution and measurement time. Usual settings for high-quality EBSPs are 15 nA current, 20 kV beam energy, 18 mm working distance, long exposure time, and minimal CCD pixel binning. The EBSD phosphor screen is set at an 18 mm working distance and a map's step size of less than 0.5 µm for strain and dislocations density analysis.

Decomposition of gaseous hydrocarbons and also hydrocarbons on the surface of samples by the electron beam inside the microscope results in carbon deposition, which degrades the quality of EBSPs inside the probed area compared to the EBSPs outside the acquisition window. The gradient of pattern degradation increases moving inside the probed zone with an apparent accumulation of deposited carbon. The black spots from the beam instant-induced carbon deposition also highlight the immediate deposition even if agglomeration did not happen.

Depth resolution

Further information: Physics:Electron scattering

Electron-matter interaction volume and various types of signal generated

There is no agreement about the definition of depth resolution. For example, it can be defined as the depth where ~92% of the signal is generated, or defined by pattern quality, or can be as ambiguous as "where useful information is obtained". Even for a given definition, depth resolution increases with electron energy and decreases with the average atomic mass of the elements making up the studied material: for example, it was estimated as 40 nm for Si and 10 nm for Ni at 20 kV energy. Unusually small values were reported for materials whose structure and composition vary along the thickness. For example, coating monocrystalline silicon with a few nm of amorphous chromium reduces the depth resolution to a few nm at 15 kV energy. In contrast, Isabell and David concluded that depth resolution in homogeneous crystals could also extend up to 1 µm due to inelastic scattering (including tangential smearing and channelling effect).

A recent comparison between reports on EBSD depth resolution, Koko et al indicated that most publications do not present a rationale for the definition of depth resolution, while not including information on the beam size, tilt angle, beam-to-sample and sample-to-detector distances. These are critical parameters for determining or simulating the depth resolution. The beam current is generally not considered to affect the depth resolution in experiments or simulations. However, it affects the beam spot size and signal-to-noise ratio, and hence, indirectly, the details of the pattern and its depth information.

Monte Carlo simulations provide an alternative approach to quantifying the depth resolution for EBSPs formation, which can be estimated using the Bloch wave theory, where backscattered primary electrons – after interacting with the crystal lattice – exit the surface, carrying information about the crystallinity of the volume interacting with the electrons. The backscattered electrons (BSE) energy distribution depends on the material's characteristics and the beam conditions. This BSE wave field is also affected by the thermal diffuse scattering process that causes incoherent and inelastic (energy loss) scattering – after the elastic diffraction events – which does not, yet, have a complete physical description that can be related to mechanisms that constitute EBSP depth resolution.

Both the EBSD experiment and simulations typically make two assumptions: that the surface is pristine and has a homogeneous depth resolution; however, neither of them is valid for a deformed sample.

Orientation and phase mapping

Pattern indexing

Formation of Kossel cone which intersect with CCD screen to form EBSP which can be Bravais-Miller indexed

If the setup geometry is well described, it is possible to relate the bands present in the diffraction pattern to the underlying crystal and crystallographic orientation of the material within the electron interaction volume. Each band can be indexed individually by the Miller indices of the diffracting plane which formed it. In most materials, only three bands/planes intersect and are required to describe a unique solution to the crystal orientation (based on their interplanar angles). Most commercial systems use look-up tables with international crystal databases to index. This crystal orientation relates the orientation of each sampled point to a reference crystal orientation.

Indexing is often the first step in the EBSD process after pattern collection. This allows for the identification of the crystal orientation at the single volume of the sample from where the pattern was collected. With EBSD software, pattern bands are typically detected via a mathematical routine using a modified Hough transform, in which every pixel in Hough space denotes a unique line/band in the EBSP. The Hough transform enables band detection, which is difficult to locate by computer in the original EBSP. Once the band locations have been detected, it is possible to relate these locations to the underlying crystal orientation, as angles between bands represent angles between lattice planes. Thus, an orientation solution can be determined when the position/angles between three bands are known. In highly symmetric materials, more than three bands are typically used to obtain and verify the orientation measurement.

The diffraction pattern is pre-processed to remove noise, correct for detector distortions, and normalise the intensity. Then, the pre-processed diffraction pattern is compared to a library of reference patterns for the material being studied. The reference patterns are generated based on the material's known crystal structure and the crystal lattice's orientation. The orientation of the crystal lattice that would generate the best match to the measured pattern is determined using a variety of algorithms. There are three leading methods of indexing that are performed by most commercial EBSD software: triplet voting; minimising the 'fit' between the experimental pattern and a computationally determined orientation, and or/and neighbour pattern averaging and re-indexing, NPAR). Indexing then give a unique solution to the single crystal orientation that is related to the other crystal orientations within the field-of-view.

Triplet voting involves identifying multiple 'triplets' associated with different solutions to the crystal orientation; each crystal orientation determined from each triplet receives one vote. Should four bands identify the same crystal orientation, then four (four choose three, i.e. [math]\displaystyle{ C(4,3) }[/math]) votes will be cast for that particular solution. Thus the candidate orientation with the highest number of votes will be the most likely solution to the underlying crystal orientation present. The number of votes for the solution chosen compared to the total number of votes describes the confidence in the underlying solution. Care must be taken in interpreting this 'confidence index' as some pseudo-symmetric orientations may result in low confidence for one candidate solution vs another. Minimising the fit involves starting with all possible orientations for a triplet. More bands are included, which reduces the number of candidate orientations. As the number of bands increases, the number of possible orientations converges ultimately to one solution. The 'fit' between the measured orientation and the captured pattern can be determined.

Overall, indexing diffraction patterns in EBSD involves a complex set of algorithms and calculations, but is essential for determining the crystallographic structure and orientation of materials at a high spatial resolution. The indexing process is continually evolving, with new algorithms and techniques being developed to improve the accuracy and speed of the process. Afterwards, a confidence index is calculated to determine the quality of the indexing result. The confidence index is based on the match quality between the measured and reference patterns. In addition, it considers factors such as noise level, detector resolution, and sample quality.

While this geometric description related to the kinematic solution using the Bragg condition is very powerful and useful for orientation and texture analysis, it only describes the geometry of the crystalline lattice. It ignores many physical processes involved within the diffracting material. To adequately describe finer features within the electron beam scattering pattern (EBSP), one must use a many-beam dynamical model (e.g. the variation in band intensities in an experimental pattern does not fit the kinematic solution related to the structure factor).

Pattern centre

To relate the orientation of a crystal, much like in X-ray diffraction (XRD), the geometry of the system must be known. In particular, the pattern centre describes the distance of the interaction volume to the detector and the location of the nearest point between the phosphor and the sample, on the phosphor screen. Early work used a single crystal of known orientation being inserted into the SEM chamber, and a particular feature of the EBSP was known to correspond to the pattern centre. Later developments involved exploiting various geometric relationships between the generation of an EBSP and the chamber geometry (shadow casting and phosphor movement).

Unfortunately, each of these methods is cumbersome and can be prone to some systematic errors for a general operator. Typically they cannot be easily used in modern SEMs with multiple designated uses. Thus, most commercial EBSD systems use the indexing algorithm combined with an iterative movement of crystal orientation and suggested pattern centre location. Minimising the fit between bands located within experimental patterns and those in look-up tables tends to converge on the pattern centre location to an accuracy of ~0.5–1% of the pattern width.

The recent development of AstroEBSD and PCGlobal, open-source MATLAB codes, increased the precision of determining the pattern centre (PC) and – consequently – elastic strains by using a pattern matching approach which simulates the pattern using EMSoft.

EBSD mapping

A map of indexed EBSD orientations for a ferrous martensite with high-angle (>10°) boundaries

The indexing results are used to generate a map of the crystallographic orientation at each point on the surface being studied. Thus, scanning the electron beam in a prescribed fashion (typically in a square or hexagonal grid, correcting for the image foreshortening due to the sample tilt) results in many rich microstructural maps. These maps can spatially describe the crystal orientation of the material being interrogated and can be used to examine microtexture and sample morphology. Some maps describe grain orientation, boundary, and diffraction pattern (image) quality. Various statistical tools can measure the average misorientation, grain size, and crystallographic texture. From this dataset, numerous maps, charts and plots can be generated. The orientation data can be visualised using a variety of techniques, including colour-coding, contour lines, and pole figures.

Microscope misalignment, image shift, scan distortion that increases with decreasing magnification, roughness and contamination of the specimen surface, boundary indexing failure and detector quality can lead to uncertainties in determining the crystal orientation. The EBSD signal-to-noise ratio depends on the material and decreases at excessive acquisition speed and beam current, thereby affecting the angular resolution of the measurement.

Strain measurement

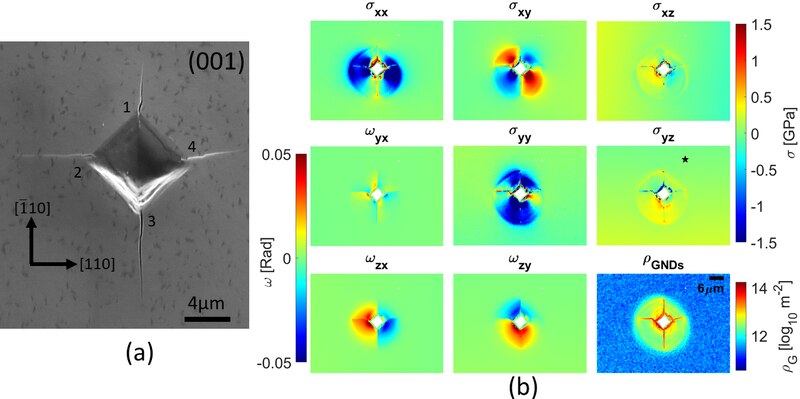
Full-field displacement, elastic strain, and the GND density provide quantifiable information about the material's elastic and plastic behaviour at the microscale. Measuring strain at the microscale requires careful consideration of other key details besides the change in length/shape (e.g., local texture, individual grain orientations). These micro-scale features can be measured using different techniques, e.g., hole drilling, monochromatic or polychromatic energy-dispersive X-ray diffraction or neutron diffraction (ND). EBSD has a high spatial resolution and is relatively sensitive and easy to use compared to other techniques. Strain measurements using EBSD can be performed at a high spatial resolution, allowing researchers to study the local variation in strain within a material. This information can be used to study the deformation and mechanical behaviour of materials, to develop models of material behaviour under different loading conditions, and to optimise the processing and performance of materials. Overall, strain measurement using EBSD is a powerful tool for studying the deformation and mechanical behaviour of materials, and is widely used in materials science and engineering research and development.

Earlier trials

The change and degradation in electron backscatter patterns (EBSPs) provide information about the diffracting volume. Pattern degradation (i.e., diffuse quality) can be used to assess the level of plasticity through the pattern/image quality (IQ), where IQ is calculated from the sum of the peaks detected when using the conventional Hough transform. Wilkinson first used the changes in high-order Kikuchi line positions to determine the elastic strains, albeit with low precision (0.3% to 1%); however, this approach cannot be used for characterising residual elastic strain in metals as the elastic strain at the yield point is usually around 0.2%. Measuring strain by tracking the change in the higher-order Kikuchi lines is practical when the strain is small, as the band position is sensitive to changes in lattice parameters. In the early 1990s, Troost et al. and Wilkinson et al. used pattern degradation and change in the zone axis position to measure the residual elastic strains and small lattice rotations with a 0.02% precision.

High-resolution electron backscatter diffraction (HR-EBSD)

Schematic shifting between a reference and deformed crystals in the EBSP pattern projected on the phosphor screen

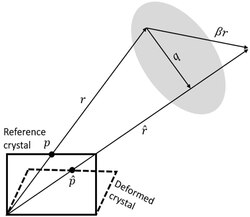
Cross-correlation-based, high angular resolution electron backscatter diffraction (HR-EBSD) – introduced by Wilkinson et al. – is an SEM-based technique to map relative elastic strains and rotations, and estimate the geometrically necessary dislocation (GND) density in crystalline materials. HR-EBSD method uses image cross-correlation to measure pattern shifts between regions of interest (ROI) in different electron backscatter diffraction patterns (EBSPs) with sub-pixel precision. As a result, the relative lattice distortion between two points in a crystal can be calculated using pattern shifts from at least four non-collinear ROI. In practice, pattern shifts are measured in more than 20 ROI per EBSP to find a best-fit solution to the deformation gradient tensor, representing the relative lattice distortion.

The displacement gradient tensor ([math]\displaystyle{ \beta }[/math]) (or local lattice distortion) relates the measured geometrical shifts in the pattern between the collected point ([math]\displaystyle{ \widehat{p} }[/math]) and associate (non-coplanar) vector ([math]\displaystyle{ \widehat{r} }[/math]), and reference point ([math]\displaystyle{ p }[/math]) pattern and associate vector ([math]\displaystyle{ r }[/math]). Thus, the (pattern shift) vector ([math]\displaystyle{ q }[/math]) can be written as in the equations below, where [math]\displaystyle{ x_{i} }[/math] and [math]\displaystyle{ u_{i} }[/math] are the direction and displacement in [math]\displaystyle{ i }[/math]th direction, respectively.

[math]\displaystyle{ q=\beta r-(\beta r.\widehat{r})\widehat{r} }[/math]

[math]\displaystyle{ \beta=\begin{pmatrix} {\partial u_1 \over x_1} & {\partial u_1 \over x_2} &{\partial u_1 \over x_3} \\{\partial u_2 \over x_1} & {\partial u_2 \over x_2} &{\partial u_2 \over x_3} \\{\partial u_3 \over x_1} & {\partial u_3 \over x_2} &{\partial u_3 \over x_3} \end{pmatrix}, \qquad r=\begin{pmatrix} {r_1} \\{r_2} \\{r_3} \\\end{pmatrix} }[/math]

The shifts are measured in the phosphor (detector) plane ([math]\displaystyle{ \beta_3 r_3=0 }[/math]), and the relationship is simplified; thus, eight out of the nine displacement gradient tensor components can be calculated by measuring the shift at four distinct, widely spaced regions on the EBSP. This shift is then corrected to the sample frame (flipped around Y-axis) because EBSP is recorded on the phosphor screen and is inverted as in a mirror. They are then corrected around the X-axis by 24° (i.e., 20° sample tilt plus ≈4° camera tilt and assuming no angular effect from the beam movement). Using infinitesimal strain theory, the deformation gradient is then split into elastic strain (symmetric part, where [math]\displaystyle{ ij=ji }[/math]), [math]\displaystyle{ e_{ij} }[/math]and lattice rotations (asymmetric part, where [math]\displaystyle{ ii=jj=0 }[/math]), [math]\displaystyle{ \omega_{ij} }[/math].

[math]\displaystyle{ e_{ij}={1\over{2}}(\beta_{ij}+\beta^{r}_{ij}), \qquad \omega_{ij}={1\over{2}}(\beta_{ij}-\beta^{r}_{ij}) }[/math]

These measurements do not provide information about the volumetric/hydrostatic strain tensors. By imposing a boundary condition that the stress normal to the surface ([math]\displaystyle{ \sigma_{33} }[/math]) is zero (i.e., traction-free surface), and using Hooke's law with anisotropic elastic stiffness constants, the missing ninth degree of freedom can be estimated in this constrained minimisation problem by using a nonlinear solver.

[math]\displaystyle{ \sigma_{33}=C_{33kl}e_{kl}=0 }[/math]

Where [math]\displaystyle{ C }[/math] is the crystal anisotropic stiffness tensor. These two equations are solved to re-calculate the refined elastic deviatoric strain ([math]\displaystyle{ \varepsilon_{kl} }[/math]), including the missing ninth (spherical) strain tensor. An alternative approach that considers the full [math]\displaystyle{ \beta }[/math] can be found in.

[math]\displaystyle{ e_{ij}=\begin{pmatrix} {e_{11}} \\{e_{22}} \\{e_{33}}\\{2e_{12}}\\{2e_{13}}\\{2e_{23}} \\\end{pmatrix}, \qquad \begin{pmatrix} {k_{1}} \\{k_{2}} \\{k_{3}} \\\end{pmatrix}=\begin{pmatrix} {e_{11}-e_{33}} \\{e_{22}-e_{33}} \\{e_{12}C_{3312}+e_{13}C_{3313}+e_{23}C_{3323}} \\\end{pmatrix} }[/math]

[math]\displaystyle{ \varepsilon_{33}={k_1C_{1133}+k_2C{2233}+k_3\over C_{1133}+C_{2233}+C_{3333}},\qquad \therefore\varepsilon_{kl}=\begin{pmatrix} {k_1+\varepsilon_{33}} \\{k_2+\varepsilon_{33}} \\{\varepsilon_{33}}\\{2e_{12}}\\{2e_{13}}\\{2e_{23}} \\\end{pmatrix} }[/math]

Finally, the stress and strain tensors are linked using the crystal anisotropic stiffness tensor ([math]\displaystyle{ C_{klij} }[/math]), and by using the Einstein summation convention with symmetry of stress tensors ([math]\displaystyle{ \sigma_{ij}=\sigma_{ji} }[/math]).

[math]\displaystyle{ \sigma_{ij}=C_{ijkl}\varepsilon_{kl} }[/math]

The quality of the produced data can be assessed by taking the geometric mean of all the ROI's correlation intensity/peaks. A value lower than 0.25 should indicate problems with the EBSPs' quality. Furthermore, the geometrically necessary dislocation (GND) density can be estimated from the HR-EBSD measured lattice rotations by relating the rotation axis and angle between neighbour map points to the dislocation types and densities in a material using Nye's tensor.

Precision and development

The HR-EBSD method can achieve a precision of ±10⁻⁴ in components of the displacement gradient tensors (i.e., variations in lattice strain and lattice rotation in radians) by measuring the shifts of zone axes within the pattern image with a resolution of ±0.05 pixels. It was limited to small strains and rotations (>1.5°) until Britton and Wilkinson and Maurice et al. raised the rotation limit to ~11° by using a re-mapping technique that recalculated the strain after transforming the patterns with a rotation matrix ([math]\displaystyle{ R }[/math]) calculated from the first cross-correlation iteration.

[math]\displaystyle{ R=\begin{pmatrix} \cos \omega_{12} & \sin \omega_{12} & 0 \\ -\sin \omega_{12} & \cos \omega_{12} & 0\\ 0 & 0& 1 \end{pmatrix} \begin{pmatrix} 1&0&0\\0&\cos \omega_{23} & \sin \omega_{23} \\ 0&-\sin \omega_{23} & \cos \omega_{23} \end{pmatrix} \begin{pmatrix} \cos \omega_{31} &0& -\sin \omega_{31} \\ 0 & 1& 0 \\ \sin \omega_{31}&0 & \cos \omega_{31} \end{pmatrix} }[/math]

(a) Secondary electron (SE) image for the indentation on the (001) mono crystal. (b) HR-EBSD stress and rotation components, and geometrical necessary dislocations density ([math]\displaystyle{ \rho_{GND} }[/math]). The location of EBSP₀ is highlighted with a star in [math]\displaystyle{ \sigma_{yz} }[/math]. The step size is 250 nm

However, further lattice rotation, typically caused by severe plastic deformations, produced errors in the elastic strain calculations. To address this problem, Ruggles et al. improved the HR-EBSD precision, even at 12° of lattice rotation, using the inverse compositional Gauss–Newton-based (ICGN) method instead of cross-correlation. For simulated patterns, Vermeij and Hoefnagels also established a method that achieves a precision of ±10⁻⁵ in the displacement gradient components using a full-field integrated digital image correlation (IDIC) framework instead of dividing the EBSPs into small ROIs. Patterns in IDIC are distortion-corrected to negate the need for re-mapping up to ~14°.

Conventional Hough transform EBSD and HR-EBSD

	Conventional EBSD	HR-EBSD
Absolute orientation	2°	N/A
Misorientation	0.1° to 0.5°	0.006° (1×10−4 rad)
GND @ 1 µm step In lines/m2 (b = 0.3 nm)	> 3×1013	> 3×1011
Relative residual strain	N/A	Deviatoric elastic strain 1×10−4
Example tasks	Texture, microstructure, etc.	Deformation

These measurements do not provide information about the hydrostatic or volumetric strains, because there is no change in the orientations of lattice planes (crystallographic directions), but only changes in the position and width of the Kikuchi bands.

The reference pattern problem

In HR-EBSD analysis, the lattice distortion field is calculated relative to a reference pattern or point (EBSP₀) per grain in the map, and is dependent on the lattice distortion at the point. The lattice distortion field in each grain is measured with respect to this point; therefore, the absolute lattice distortion at the reference point (relative to the unstrained crystal) is excluded from the HR-EBSD elastic strain and rotation maps. This ‘reference pattern problem’ is similar to the ‘d₀ problem’ in X-ray diffraction, and affects the nominal magnitude of HR-EBSD stress fields. However, selecting the reference pattern (EBSP₀) plays a key role, as severely deformed EBSP₀ adds phantom lattice distortions to the map values, thus, decreasing the measurement precision.

Linear correlation coefficients between the local conditions at the EBSP0 point and the averaged conditions at the grain for the ferrite (Fe-α) and austenite (Fe-γ) phase of age-hardened DSS, and Silicon (Si). The analysis considers the average deformation gradient tensor determinant ([math]\displaystyle{ A^{0} }[/math]), maximum in-plane principal strain ([math]\displaystyle{ \epsilon_{MAX} }[/math]), rotation magnitude ([math]\displaystyle{ \omega_{T}=\sqrt(\omega_{32}^2+\omega_{13}^2+\omega_{21}^2) }[/math]), correlation peak height (PH), mean angular error (MAE) and GND density.

The local lattice distortion at the EBSP₀ influences the resultant HR-EBSD map, e.g., a reference pattern deformed in tension will directly reduce the HR-EBSD map tensile strain magnitude while indirectly influencing the other component magnitude and the strain's spatial distribution. Furthermore, the choice of EBSP₀ slightly affects the GND density distribution and magnitude, and choosing a reference pattern with a higher GND density reduces the cross-correlation quality, changes the spatial distribution and induces more errors than choosing a reference pattern with high lattice distortion. Additionally, there is no apparent connection between EBSP₀’s IQ and EBSP₀'s local lattice distortion.

The use of simulated reference patterns for absolute strain measurement is still an active area of research and scrutiny as difficulties arise from the variation of inelastic electron scattering with depth which limits the accuracy of dynamical diffraction simulation models, and imprecise determination of the pattern centre which leads to phantom strain components which cancel out when using experimentally acquired reference patterns. Other methods assumed that absolute strain at EBSP₀ can be determined using crystal plasticity finite-element (CPFE) simulations, which then can be then combined with the HR-EBSD data (e.g., using linear ‘top-up’ method or displacement integration) to calculate the absolute lattice distortions.

In addition, GND density estimation is nominally insensitive to (or negligibly dependent upon) EBSP₀ choice, as only neighbour point-to-point differences in the lattice rotation maps are used for GND density calculation. However, this assumes that the absolute lattice distortion of EBSP₀ only changes the relative lattice rotation map components by a constant value which vanishes during derivative operations, i.e., lattice distortion distribution is insensitive to EBSP₀ choice.

Selecting a reference pattern

Criteria for EBSP₀ selection can be one or a mixture of:

• Selecting from points with low GND density or low Kernel average misorientation (KAM) based on the Hough measured local grain misorientations;
• Selecting from points with high image quality (IQ), which may have a low defect density within its electron interaction volume, is therefore assumed to be a low-strained region of a polycrystalline material. However, IQ does not carry a clear physical meaning, and the magnitudes of the measured relative lattice distortion are insensitive to the IQ of EBSP₀;
• EBSP₀ can also be manually selected to be far from potential stress concentrations such as grain boundaries, inclusions, or cracks using subjective criteria;
• Selecting an EBSP₀ after examining the empirical relationship between the cross-correlation parameter and angular error, used in an iterative algorithm to identify the optimal reference pattern that maximises the precision of HR-EBSD.

These criteria assume these parameters can indicate the strain conditions at the reference point, which can produce an accurate measurements of up to 3.2×10⁻⁴ elastic strain. However, experimental measurements point to the inaccuracy of HR-EBSD in determining the out-of-plane shear strain components distribution and magnitude.

Applications

EBSD is used in a wide range of applications, including materials science and engineering, geology, and biological research. In materials science and engineering, EBSD is used to study the microstructure of metals, ceramics, and polymers, and to develop models of material behaviour. In geology, EBSD is used to study the crystallographic structure of minerals and rocks. In biological research, EBSD is used to study the microstructure of biological tissues and to investigate the structure of biological materials such as bone and teeth.

Scattered electron imaging

The EBSD detector has forward scattered electron diodes (FSDs) at the bottom, in the middle (MSD) and at the top of the detector.

Far-field image of 475 °C embrittled duplex stainless steel with the virtual forward-scatter detector (VFSD) positioned at 38 mm from the sample

EBSD detectors can have forward scattered electron diodes (FSD) at the bottom, in the middle (MSD) and at the top of the detector. Forward-scattered electron (FSE) imaging involves collecting electrons scattered at small angles from the surface of a sample, which provides information about the surface topography and composition. The FSE signal is also sensitive to the crystallographic orientation of the sample. By analysing the intensity and contrast of the FSE signal, researchers can determine the crystallographic orientation of each pixel in the image.

The FSE signal is typically collected simultaneously with the BSE signal in EBSD analysis. The BSE signal is sensitive to the average atomic number of the sample, and is used to generate an image of the surface topography and composition. The FSE signal is superimposed on the BSE image to provide information about the crystallographic orientation.

Image generation has a lot of freedom when using the EBSD detector as an imaging device. An image created using a combination of diodes is called virtual or VFSD. It is possible to acquire images at a rate akin to slow scan imaging in the SEM by excessive binning of the EBSD CCD camera. It is possible to suppress or isolate the contrast of interest by creating composite images from simultaneously captured images, which offers a wide range of combinations for assessing various microstructure characteristics. Nevertheless, VFSD images do not include the quantitative information inherent to traditional EBSD maps; they simply offer representations of the microstructure.

Integrated EBSD/EDS mapping

When simultaneous EDS/EBSD collection can be achieved, the capabilities of both techniques can be enhanced. There are applications where sample chemistry or phase cannot be differentiated via EDS alone because of similar composition, and structure cannot be solved with EBSD alone because of ambiguous structure solutions. To accomplish integrated mapping, the analysis area is scanned, and at each point, Hough peaks and EDS region-of-interest counts are stored. Positions of phases are determined in X-ray maps, and each element's measured EDS intensities are given in charts. The chemical intensity ranges are set for each phase to select the grains. All patterns are then re-indexed off-line. The recorded chemistry determines which phase/crystal-structure file is used to index each point. Each pattern is indexed by only one phase, and maps displaying distinguished phases are generated. The interaction volumes for EDS and EBSD are significantly different (on the order of micrometres compared to tens of nanometres), and the shape of these volumes using a highly tilted sample may have implications on algorithms for phase discrimination.

EBSD, when used together with other in-SEM techniques such as cathodoluminescence (CL), wavelength dispersive X-ray spectroscopy (WDS) and/or EDS can provide a deeper insight into the specimen's properties and enhance phase identification. For example, the minerals calcite (limestone) and aragonite (shell) have the same chemical composition – calcium carbonate (CaCO₃) therefore EDS/WDS cannot tell them apart, but they have different microcrystalline structures so EBSD can differentiate between them.

Integrated EBSD/DIC mapping

EBSD and digital image correlation (DIC) can be used together to analyse the microstructure and deformation behaviour of materials. DIC is a method that uses digital image processing techniques to measure deformation and strain fields in materials. By combining EBSD and DIC, researchers can obtain both crystallographic and mechanical information about a material simultaneously. This allows for a more comprehensive understanding of the relationship between microstructure and mechanical behaviour, which is particularly useful in fields such as materials science and engineering.

DIC can identify regions of strain localisation in a material, while EBSD can provide information about the microstructure in these regions. By combining these techniques, researchers can gain insights into the mechanisms responsible for the observed strain localisation. For example, EBSD can be used to determine the grain orientations and boundary misorientations before and after deformation. In contrast, DIC can be used to measure the strain fields in the material during deformation. Or EBSD can be used to identify the activation of different slip systems during deformation, while DIC can be used to measure the associated strain fields. By correlating these data, researchers can better understand the role of different deformation mechanisms in the material's mechanical behaviour.

Overall, the combination of EBSD and DIC provides a powerful tool for investigating materials' microstructure and deformation behaviour. This approach can be applied to a wide range of materials and deformation conditions and has the potential to yield insights into the fundamental mechanisms underlying mechanical behaviour.

3D EBSD

3D EBSD map for WC-6%Co with 62 slices of 10×10×3 mm size and 50 nm resolution in x, y and z directions

3D EBSD combines EBSD with serial sectioning methods to create a three-dimensional map of a material's crystallographic structure. The technique involves serially sectioning a sample into thin slices, and then using EBSD to map the crystallographic orientation of each slice. The resulting orientation maps are then combined to generate a 3D map of the crystallographic structure of the material. The serial sectioning can be performed using a variety of methods, including mechanical polishing, focused ion beam (FIB) milling, or ultramicrotomy. The choice of sectioning method depends on the size and shape of the sample, on its chemical composition, reactivity and mechanical properties, as well as the desired resolution and accuracy of the 3D map.

3D EBSD has several advantages over traditional 2D EBSD. First, it provides a complete picture of a material's crystallographic structure, allowing for a more accurate and detailed analysis of the microstructure. Second, it can be used to study complex microstructures, such as those found in composite materials or multi-phase alloys. Third, it can be used to study the evolution of microstructure over time, such as during deformation or heat treatment.

However, 3D EBSD also has some limitations. It requires extensive data acquisition and processing, proper alignment between slices, and can be time-consuming and computationally intensive. In addition, the quality of the 3D map depends on the quality of the individual EBSD maps, which can be affected by factors such as sample preparation, data acquisition parameters, and analysis methods. Overall, 3D EBSD is a powerful technique for studying the crystallographic structure of materials in three dimensions, and is widely used in materials science and engineering research and development.

Further reading

• "Electron Backscatter Diffraction (EBSD)". https://www.doitpoms.ac.uk/tlplib/crystallographic_texture/ebsd.php. 
• Britton, T. Ben; Jiang, Jun; Guo, Y.; Vilalta-Clemente, A.; Wallis, D.; Hansen, L.N.; Winkelmann, A.; Wilkinson, A.J. (July 2016). "Tutorial: Crystal orientations and EBSD — Or which way is up?". Materials Characterization 117: 113–126. doi:10.1016/j.matchar.2016.04.008. 
• Charpagne, Marie-Agathe; Strub, Florian; Pollock, Tresa M. (April 2019). "Accurate reconstruction of EBSD datasets by a multimodal data approach using an evolutionary algorithm". Materials Characterization 150: 184–198. doi:10.1016/j.matchar.2019.01.033. 
• Jackson, M. A.; Pascal, E.; De Graef, M. (2019). "Dictionary Indexing of Electron Back-Scatter Diffraction Patterns: a Hands-On Tutorial". Integrating Materials and Manufacturing Innovation 8 (2): 226–246. doi:10.1007/s40192-019-00137-4. https://link.springer.com/article/10.1007/s40192-019-00137-4. 
• Randle, Valerie (September 2009). "Electron backscatter diffraction: Strategies for reliable data acquisition and processing". Materials Characterization 60 (90): 913–922. doi:10.1016/j.matchar.2009.05.011. 
• Electron Backscatter Diffraction in Materials Science (2nd ed.). New York, New York: Springer New York, New York. 2009 (published 12 August 2009). doi:10.1007/978-0-387-88136-2. ISBN 978-0-387-88135-5. 
• Zaefferer, S.; Raabe, D.; A., Khorashadizadeh. "Tomographic orientation microscopy (3D EBSD) on steels using a joint FIB SEM technique". https://www.mpie.de/2991103/Tomographic_orientation_microscopy_3D_EBSD_on_steels. 

External links

Codes

• De Graef, M. (July 2017). "EMsoft (simulate EBSP)". https://github.com/EMsoft-org/EMsoft. 
• Hielscher, Schaeben (2008). "MTEX (EBSD analysis)". https://mtex-toolbox.github.io/. 
• Ruggles, T. J.; Bomarito, G. F.; Qiu, R. L.; Hochhalter, J. D. (2018-12-01). "OpenXY (HR-EBSD)". https://github.com/BYU-MicrostructureOfMaterials/OpenXY. 
• Tong, Vivian; Britton, Ben (July 2017). "TrueEBSD: correcting spatial distortions in electron backscatter diffraction maps". Ultramicroscopy 221: 113130. doi:10.1016/j.ultramic.2020.113130. PMID 33290982. https://zenodo.org/record/4282885. 

Videos

• Britton, Ben (2021-01-11). Introduction to EBSD: Section 1 - What can EBSD tell you?. YouTube.
• Nowell, Matt (2022-02-22). Learn How I Prepare Samples for EBSD Analysis. EDAX (YouTube).
• Wright, Stuart (2022-01-31). EBSD Analysis of Deformed Microstructures. EDAX (YouTube).
• Electron Backscatter Diffraction Explained: QUANTAX EBSD. Bruker Nano Analytics (YouTube). 2020-09-01.