Physics:Maxwell–Boltzmann statistics

Maxwell–Boltzmann statistics can be used to derive the Maxwell–Boltzmann distribution of particle speeds in an ideal gas. Shown: distribution of particle speed for 10⁶ oxygen particles at -100, 20 and 600 °C.

In statistical mechanics, Maxwell–Boltzmann statistics describes the distribution of classical material particles over various energy states in thermal equilibrium. It is applicable when the temperature is high enough or the particle density is low enough to render quantum effects negligible.

The expected number of particles with energy [math]\displaystyle{ \varepsilon_i }[/math] for Maxwell–Boltzmann statistics is

[math]\displaystyle{ \langle N_i \rangle = \frac {g_i} {e^{(\varepsilon_i - \mu)/kT}} = \frac{N}{Z}\,g_i e^{-\varepsilon_i/kT}, }[/math]

where:

• [math]\displaystyle{ \varepsilon_i }[/math] is the energy of the i-th energy level,
• [math]\displaystyle{ \langle N_i \rangle }[/math] is the average number of particles in the set of states with energy [math]\displaystyle{ \varepsilon_i }[/math],
• [math]\displaystyle{ g_i }[/math] is the degeneracy of energy level i, that is, the number of states with energy [math]\displaystyle{ \varepsilon_i }[/math] which may nevertheless be distinguished from each other by some other means,
• μ is the chemical potential,
• k is the Boltzmann constant,
• T is absolute temperature,
• N is the total number of particles: [math]\displaystyle{ N = \sum_i N_i, }[/math]
• Z is the partition function: [math]\displaystyle{ Z = \sum_i g_i e^{-\varepsilon_i/kT}, }[/math]
• e is Euler's number

Equivalently, the number of particles is sometimes expressed as

[math]\displaystyle{ \langle N_i \rangle = \frac {1} {e^{(\varepsilon_i - \mu)/kT}} = \frac{N}{Z}\,e^{-\varepsilon_i/kT}, }[/math]

where the index i now specifies a particular state rather than the set of all states with energy [math]\displaystyle{ \varepsilon_i }[/math], and [math]\displaystyle{ Z = \sum_i e^{-\varepsilon_i/kT} }[/math].

History

Further information: Maxwell–Boltzmann distribution

Maxwell–Boltzmann statistics grew out of the Maxwell–Boltzmann distribution, most likely as a distillation of the underlying technique. The distribution was first derived by Maxwell in 1860 on heuristic grounds. Boltzmann later, in the 1870s, carried out significant investigations into the physical origins of this distribution. The distribution can be derived on the ground that it maximizes the entropy of the system.

Applicability

Comparison of average occupancy of the ground state for three statistics

Maxwell–Boltzmann statistics is used to derive the Maxwell–Boltzmann distribution of an ideal gas. However, it can also be used to extend that distribution to particles with a different energy–momentum relation, such as relativistic particles (resulting in Maxwell–Jüttner distribution), and to other than three-dimensional spaces.

Maxwell–Boltzmann statistics is often described as the statistics of "distinguishable" classical particles. In other words, the configuration of particle A in state 1 and particle B in state 2 is different from the case in which particle B is in state 1 and particle A is in state 2. This assumption leads to the proper (Boltzmann) statistics of particles in the energy states, but yields non-physical results for the entropy, as embodied in the Gibbs paradox.

At the same time, there are no real particles that have the characteristics required by Maxwell–Boltzmann statistics. Indeed, the Gibbs paradox is resolved if we treat all particles of a certain type (e.g., electrons, protons, etc.) as principally indistinguishable. Once this assumption is made, the particle statistics change. The change in entropy in the entropy of mixing example may be viewed as an example of a non-extensive entropy resulting from the distinguishability of the two types of particles being mixed.

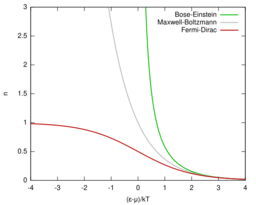
Quantum particles are either bosons (following instead Bose–Einstein statistics) or fermions (subject to the Pauli exclusion principle, following instead Fermi–Dirac statistics). Both of these quantum statistics approach the Maxwell–Boltzmann statistics in the limit of high temperature and low particle density.

Derivations

Maxwell–Boltzmann statistics can be derived in various statistical mechanical thermodynamic ensembles:

• The grand canonical ensemble, exactly.
• The canonical ensemble, exactly.
• The microcanonical ensemble, but only in the thermodynamic limit.

In each case it is necessary to assume that the particles are non-interacting, and that multiple particles can occupy the same state and do so independently.

Derivation from microcanonical ensemble

Suppose we have a container with a huge number of very small particles all with identical physical characteristics (such as mass, charge, etc.). Let's refer to this as the system. Assume that though the particles have identical properties, they are distinguishable. For example, we might identify each particle by continually observing their trajectories, or by placing a marking on each one, e.g., drawing a different number on each one as is done with lottery balls.

The particles are moving inside that container in all directions with great speed. Because the particles are speeding around, they possess some energy. The Maxwell–Boltzmann distribution is a mathematical function that describes about how many particles in the container have a certain energy. More precisely, the Maxwell–Boltzmann distribution gives the non-normalized probability (this means that the probabilities do not add up to 1) that the state corresponding to a particular energy is occupied.

In general, there may be many particles with the same amount of energy [math]\displaystyle{ \varepsilon }[/math]. Let the number of particles with the same energy [math]\displaystyle{ \varepsilon_1 }[/math] be [math]\displaystyle{ N_1 }[/math], the number of particles possessing another energy [math]\displaystyle{ \varepsilon_2 }[/math] be [math]\displaystyle{ N_2 }[/math], and so forth for all the possible energies [math]\displaystyle{ \{ \varepsilon_i \mid i = 1, 2, 3, \ldots\}. }[/math] To describe this situation, we say that [math]\displaystyle{ N_i }[/math] is the occupation number of the energy level [math]\displaystyle{ i. }[/math] If we know all the occupation numbers [math]\displaystyle{ \{N_i \mid i=1,2,3,\ldots\}, }[/math] then we know the total energy of the system. However, because we can distinguish between which particles are occupying each energy level, the set of occupation numbers [math]\displaystyle{ \{ N_i \mid i=1,2,3,\ldots\} }[/math] does not completely describe the state of the system. To completely describe the state of the system, or the microstate, we must specify exactly which particles are in each energy level. Thus when we count the number of possible states of the system, we must count each and every microstate, and not just the possible sets of occupation numbers.

To begin with, assume that there is only one state at each energy level [math]\displaystyle{ i }[/math] (there is no degeneracy). What follows next is a bit of combinatorial thinking which has little to do in accurately describing the reservoir of particles. For instance, let's say there is a total of [math]\displaystyle{ k }[/math] boxes labelled [math]\displaystyle{ a,b,\ldots,k }[/math]. With the concept of combination, we could calculate how many ways there are to arrange [math]\displaystyle{ N }[/math] into the set of boxes, where the order of balls within each box isn’t tracked. First, we select [math]\displaystyle{ N_a }[/math] balls from a total of [math]\displaystyle{ N }[/math] balls to place into box [math]\displaystyle{ a }[/math], and continue to select for each box from the remaining balls, ensuring that every ball is placed in one of the boxes. The total number of ways that the balls can be arranged is

[math]\displaystyle{ \begin{align} W & = \frac{N!}{N_a!\cancel{(N-N_a)!}} \times \frac{\cancel{(N-N_a)!}}{N_b!\cancel{(N-N_a-N_b)!}} \times \frac{\cancel{(N-N_a-N_b)!}}{N_c!\cancel{(N-N_a-N_b-N_c)!}} \times \cdots \times \frac{\cancel{(N-\cdots-N_\ell)!}}{N_k!(N-\cdots-N_\ell-N_k)!} \\[8pt] & = \frac{N!}{N_a!N_b!N_c!\cdots N_k!(N-N_a-\cdots-N_\ell-N_k)!} \end{align} }[/math]

As every ball has been placed into a box, [math]\displaystyle{ (N - N_a - N_b - \cdots - N_k)! = 0! = 1 }[/math], and we simplify the expression as

[math]\displaystyle{ W = N!\prod_{\ell=a,b,\ldots}^k \frac{1}{N_\ell!} }[/math]

This is just the multinomial coefficient, the number of ways of arranging N items into k boxes, the l-th box holding N_l items, ignoring the permutation of items in each box.

Now, consider the case where there is more than one way to put [math]\displaystyle{ N_i }[/math] particles in the box [math]\displaystyle{ i }[/math] (i.e. taking the degeneracy problem into consideration). If the [math]\displaystyle{ i }[/math]-th box has a "degeneracy" of [math]\displaystyle{ g_i }[/math], that is, it has [math]\displaystyle{ g_i }[/math] "sub-boxes" ([math]\displaystyle{ g_i }[/math] boxes with the same energy [math]\displaystyle{ \varepsilon_i }[/math]. These states/boxes with the same energy are called degenerate states.), such that any way of filling the [math]\displaystyle{ i }[/math]-th box where the number in the sub-boxes is changed is a distinct way of filling the box, then the number of ways of filling the i-th box must be increased by the number of ways of distributing the [math]\displaystyle{ N_i }[/math] objects in the [math]\displaystyle{ g_i }[/math] "sub-boxes". The number of ways of placing [math]\displaystyle{ N_i }[/math] distinguishable objects in [math]\displaystyle{ g_i }[/math] "sub-boxes" is [math]\displaystyle{ g_i^{N_i} }[/math] (the first object can go into any of the [math]\displaystyle{ g_i }[/math] boxes, the second object can also go into any of the [math]\displaystyle{ g_i }[/math] boxes, and so on). Thus the number of ways [math]\displaystyle{ W }[/math] that a total of [math]\displaystyle{ N }[/math] particles can be classified into energy levels according to their energies, while each level [math]\displaystyle{ i }[/math] having [math]\displaystyle{ g_i }[/math] distinct states such that the i-th level accommodates [math]\displaystyle{ N_i }[/math] particles is:

[math]\displaystyle{ W=N!\prod_{i}\frac{g_i^{N_i}}{N_i!} }[/math]

This is the form for W first derived by Boltzmann. Boltzmann's fundamental equation [math]\displaystyle{ S=k\,\ln W }[/math] relates the thermodynamic entropy S to the number of microstates W, where k is the Boltzmann constant. It was pointed out by Gibbs however, that the above expression for W does not yield an extensive entropy, and is therefore faulty. This problem is known as the Gibbs paradox. The problem is that the particles considered by the above equation are not indistinguishable. In other words, for two particles (A and B) in two energy sublevels the population represented by [A,B] is considered distinct from the population [B,A] while for indistinguishable particles, they are not. If we carry out the argument for indistinguishable particles, we are led to the Bose–Einstein expression for W:

[math]\displaystyle{ W=\prod_i \frac{(N_i+g_i-1)!}{N_i!(g_i-1)!} }[/math]

The Maxwell–Boltzmann distribution follows from this Bose–Einstein distribution for temperatures well above absolute zero, implying that [math]\displaystyle{ g_i\gg 1 }[/math]. The Maxwell–Boltzmann distribution also requires low density, implying that [math]\displaystyle{ g_i\gg N_i }[/math]. Under these conditions, we may use Stirling's approximation for the factorial:

[math]\displaystyle{ N! \approx N^N e^{-N}, }[/math]

to write:

[math]\displaystyle{ W\approx\prod_i \frac{(N_i+g_i)^{N_i+g_i}}{N_i^{N_i}g_i^{g_i}}\approx\prod_i \frac{g_i^{N_i}(1+N_i/g_i)^{g_i}}{N_i^{N_i}} }[/math]

Using the fact that [math]\displaystyle{ (1+N_i/g_i)^{g_i}\approx e^{N_i} }[/math] for [math]\displaystyle{ g_i\gg N_i }[/math] we can again use Stirling's approximation to write:

[math]\displaystyle{ W\approx\prod_i \frac{g_i^{N_i}}{N_i!} }[/math]

This is essentially a division by N! of Boltzmann's original expression for W, and this correction is referred to as correct Boltzmann counting.

We wish to find the [math]\displaystyle{ N_i }[/math] for which the function [math]\displaystyle{ W }[/math] is maximized, while considering the constraint that there is a fixed number of particles [math]\displaystyle{ \left(N=\sum N_i\right) }[/math] and a fixed energy [math]\displaystyle{ \left(E=\sum N_i \varepsilon_i\right) }[/math] in the container. The maxima of [math]\displaystyle{ W }[/math] and [math]\displaystyle{ \ln(W) }[/math] are achieved by the same values of [math]\displaystyle{ N_i }[/math] and, since it is easier to accomplish mathematically, we will maximize the latter function instead. We constrain our solution using Lagrange multipliers forming the function:

[math]\displaystyle{ f(N_1,N_2,\ldots,N_n) = \textstyle \ln(W)+\alpha(N-\sum N_i) + \beta(E-\sum N_i \varepsilon_i) }[/math]

[math]\displaystyle{ \ln W=\ln\left[\prod_{i=1}^{n}\frac{g_i^{N_i}}{N_i!}\right] \approx \sum_{i=1}^n\left(N_i\ln g_i-N_i\ln N_i + N_i\right) }[/math]

Finally

[math]\displaystyle{ f(N_1,N_2,\ldots,N_n)=\alpha N +\beta E + \sum_{i=1}^n\left(N_i\ln g_i-N_i\ln N_i + N_i-(\alpha+\beta\varepsilon_i) N_i\right) }[/math]

In order to maximize the expression above we apply Fermat's theorem (stationary points), according to which local extrema, if exist, must be at critical points (partial derivatives vanish):

[math]\displaystyle{ \frac{\partial f}{\partial N_i}=\ln g_i-\ln N_i -(\alpha+\beta\varepsilon_i) = 0 }[/math]

By solving the equations above ([math]\displaystyle{ i=1\ldots n }[/math]) we arrive to an expression for [math]\displaystyle{ N_i }[/math]:

[math]\displaystyle{ N_i = \frac{g_i}{e^{\alpha+\beta \varepsilon_i}} }[/math]

Substituting this expression for [math]\displaystyle{ N_i }[/math] into the equation for [math]\displaystyle{ \ln W }[/math] and assuming that [math]\displaystyle{ N \gg 1 }[/math] yields:

[math]\displaystyle{ \ln W = (\alpha+1) N+\beta E\, }[/math]

or, rearranging:

[math]\displaystyle{ E=\frac{\ln W}{\beta}-\frac{N}{\beta}-\frac{\alpha N}{\beta} }[/math]

Boltzmann realized that this is just an expression of the Euler-integrated fundamental equation of thermodynamics. Identifying E as the internal energy, the Euler-integrated fundamental equation states that :

[math]\displaystyle{ E=TS-PV+\mu N }[/math]

where T is the temperature, P is pressure, V is volume, and μ is the chemical potential. Boltzmann's famous equation [math]\displaystyle{ S=k \ln W }[/math] is the realization that the entropy is proportional to [math]\displaystyle{ \ln W }[/math] with the constant of proportionality being the Boltzmann constant. Using the ideal gas equation of state (PV = NkT), It follows immediately that [math]\displaystyle{ \beta=1/kT }[/math] and [math]\displaystyle{ \alpha=-\mu/kT }[/math] so that the populations may now be written:

[math]\displaystyle{ N_i = \frac{g_i}{e^{(\varepsilon_i-\mu)/(kT)}} }[/math]

Note that the above formula is sometimes written:

[math]\displaystyle{ N_i = \frac{g_i}{e^{\varepsilon_i/kT}/z} }[/math]

where [math]\displaystyle{ z=\exp(\mu/kT) }[/math] is the absolute activity.

Alternatively, we may use the fact that

[math]\displaystyle{ \sum_i N_i=N }[/math]

to obtain the population numbers as

[math]\displaystyle{ N_i = N\frac{g_i e^{-\varepsilon_i/kT}}{Z} }[/math]

where Z is the partition function defined by:

[math]\displaystyle{ Z = \sum_i g_i e^{-\varepsilon_i/kT} }[/math]

In an approximation where ε_i is considered to be a continuous variable, the Thomas–Fermi approximation yields a continuous degeneracy g proportional to [math]\displaystyle{ \sqrt{\varepsilon} }[/math] so that:

[math]\displaystyle{ \frac{\sqrt{\varepsilon}\,e^{-\varepsilon/k T}}{\int_0^\infty\sqrt{\varepsilon}\,e^{-\varepsilon/k T}} = \frac{\sqrt{\varepsilon}\,e^{-\varepsilon/k T}}{\frac{\sqrt{\pi}}{2}(kT)^{3/2}} = \frac{2\sqrt{\varepsilon}\,e^{-\varepsilon/k T}}{\sqrt{\pi(kT)^3}} }[/math]

which is just the Maxwell–Boltzmann distribution for the energy.

Derivation from canonical ensemble

In the above discussion, the Boltzmann distribution function was obtained via directly analysing the multiplicities of a system. Alternatively, one can make use of the canonical ensemble. In a canonical ensemble, a system is in thermal contact with a reservoir. While energy is free to flow between the system and the reservoir, the reservoir is thought to have infinitely large heat capacity as to maintain constant temperature, T, for the combined system.

In the present context, our system is assumed to have the energy levels [math]\displaystyle{ \varepsilon _i }[/math] with degeneracies [math]\displaystyle{ g_i }[/math]. As before, we would like to calculate the probability that our system has energy [math]\displaystyle{ \varepsilon_i }[/math].

If our system is in state [math]\displaystyle{ \; s_1 }[/math], then there would be a corresponding number of microstates available to the reservoir. Call this number [math]\displaystyle{ \; \Omega _ R (s_1) }[/math]. By assumption, the combined system (of the system we are interested in and the reservoir) is isolated, so all microstates are equally probable. Therefore, for instance, if [math]\displaystyle{ \; \Omega _ R (s_1) = 2 \; \Omega _ R (s_2) }[/math], we can conclude that our system is twice as likely to be in state [math]\displaystyle{ \; s_1 }[/math] than [math]\displaystyle{ \; s_2 }[/math]. In general, if [math]\displaystyle{ \; P(s_i) }[/math] is the probability that our system is in state [math]\displaystyle{ \; s_i }[/math],

[math]\displaystyle{ \frac{P(s_1)}{P(s_2)} = \frac{\Omega _ R (s_1)}{\Omega _ R (s_2)}. }[/math]

Since the entropy of the reservoir [math]\displaystyle{ \; S_R = k \ln \Omega _R }[/math], the above becomes

[math]\displaystyle{ \frac{P(s_1)}{P(s_2)} = \frac{ e^{S_R(s_1)/k} }{ e^{S_R(s_2)/k} } = e^{(S_R (s_1) - S_R (s_2))/k}. }[/math]

Next we recall the thermodynamic identity (from the first law of thermodynamics):

[math]\displaystyle{ d S_R = \frac{1}{T} (d U_R + P \, d V_R - \mu \, d N_R). }[/math]

In a canonical ensemble, there is no exchange of particles, so the [math]\displaystyle{ d N_R }[/math] term is zero. Similarly, [math]\displaystyle{ d V_R = 0. }[/math] This gives

[math]\displaystyle{ S_R (s_1) - S_R (s_2) = \frac{1}{T} (U_R (s_1) - U_R (s_2)) = - \frac{1}{T} (E(s_1) - E(s_2)), }[/math]

where [math]\displaystyle{ U_R (s_i) }[/math] and [math]\displaystyle{ E(s_i) }[/math] denote the energies of the reservoir and the system at [math]\displaystyle{ s_i }[/math], respectively. For the second equality we have used the conservation of energy. Substituting into the first equation relating [math]\displaystyle{ P(s_1), \; P(s_2) }[/math]:

[math]\displaystyle{ \frac{P(s_1)}{P(s_2)} = \frac{ e^{ - E(s_1) / kT } }{ e^{ - E(s_2) / kT} }, }[/math]

which implies, for any state s of the system

[math]\displaystyle{ P(s) = \frac{1}{Z} e^{- E(s) / kT}, }[/math]

where Z is an appropriately chosen "constant" to make total probability 1. (Z is constant provided that the temperature T is invariant.)

[math]\displaystyle{ Z = \sum _s e^{- E(s) / kT}, }[/math]

where the index s runs through all microstates of the system. Z is sometimes called the Boltzmann sum over states (or "Zustandssumme" in the original German). If we index the summation via the energy eigenvalues instead of all possible states, degeneracy must be taken into account. The probability of our system having energy [math]\displaystyle{ \varepsilon _i }[/math] is simply the sum of the probabilities of all corresponding microstates:

[math]\displaystyle{ P (\varepsilon _i) = \frac{1}{Z} g_i e^{- \varepsilon_i / kT} }[/math]

where, with obvious modification,

[math]\displaystyle{ Z = \sum _j g_j e^{- \varepsilon _j / kT}, }[/math]

this is the same result as before.

Comments on this derivation:

• Notice that in this formulation, the initial assumption "... suppose the system has total N particles..." is dispensed with. Indeed, the number of particles possessed by the system plays no role in arriving at the distribution. Rather, how many particles would occupy states with energy [math]\displaystyle{ \varepsilon _i }[/math] follows as an easy consequence.
• What has been presented above is essentially a derivation of the canonical partition function. As one can see by comparing the definitions, the Boltzmann sum over states is equal to the canonical partition function.
• Exactly the same approach can be used to derive Fermi–Dirac and Bose–Einstein statistics. However, there one would replace the canonical ensemble with the grand canonical ensemble, since there is exchange of particles between the system and the reservoir. Also, the system one considers in those cases is a single particle state, not a particle. (In the above discussion, we could have assumed our system to be a single atom.)

See also

• Bose–Einstein statistics
• Fermi–Dirac statistics
• Boltzmann factor

Bibliography

• Carter, Ashley H., "Classical and Statistical Thermodynamics", Prentice–Hall, Inc., 2001, New Jersey.
• Raj Pathria, "Statistical Mechanics", Butterworth–Heinemann, 1996.