Physics:Mohr's circle

Short description: Geometric civil engineering calculation technique

Figure 1. Mohr's circles for a three-dimensional state of stress

Mohr's circle is a two-dimensional graphical representation of the transformation law for the Cauchy stress tensor.

Mohr's circle is often used in calculations relating to mechanical engineering for materials' strength, geotechnical engineering for strength of soils, and structural engineering for strength of built structures. It is also used for calculating stresses in many planes by reducing them to vertical and horizontal components. These are called principal planes in which principal stresses are calculated; Mohr's circle can also be used to find the principal planes and the principal stresses in a graphical representation, and is one of the easiest ways to do so.

After performing a stress analysis on a material body assumed as a continuum, the components of the Cauchy stress tensor at a particular material point are known with respect to a coordinate system. The Mohr circle is then used to determine graphically the stress components acting on a rotated coordinate system, i.e., acting on a differently oriented plane passing through that point.

The abscissa and ordinate ([math]\displaystyle{ \sigma_\mathrm{n} }[/math],[math]\displaystyle{ \tau_\mathrm{n} }[/math]) of each point on the circle are the magnitudes of the normal stress and shear stress components, respectively, acting on the rotated coordinate system. In other words, the circle is the locus of points that represent the state of stress on individual planes at all their orientations, where the axes represent the principal axes of the stress element.

19th-century German engineer Karl Culmann was the first to conceive a graphical representation for stresses while considering longitudinal and vertical stresses in horizontal beams during bending. His work inspired fellow German engineer Christian Otto Mohr (the circle's namesake), who extended it to both two- and three-dimensional stresses and developed a failure criterion based on the stress circle.

Alternative graphical methods for the representation of the stress state at a point include the Lamé's stress ellipsoid and Cauchy's stress quadric.

The Mohr circle can be applied to any symmetric 2x2 tensor matrix, including the strain and moment of inertia tensors.

Motivation

Figure 2. Stress in a loaded deformable material body assumed as a continuum.

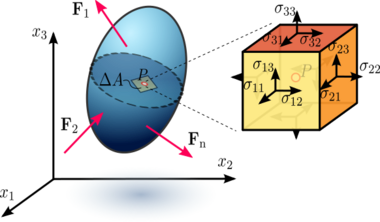
Internal forces are produced between the particles of a deformable object, assumed as a continuum, as a reaction to applied external forces, i.e., either surface forces or body forces. This reaction follows from Euler's laws of motion for a continuum, which are equivalent to Newton's laws of motion for a particle. A measure of the intensity of these internal forces is called stress. Because the object is assumed as a continuum, these internal forces are distributed continuously within the volume of the object.

In engineering, e.g., structural, mechanical, or geotechnical, the stress distribution within an object, for instance stresses in a rock mass around a tunnel, airplane wings, or building columns, is determined through a stress analysis. Calculating the stress distribution implies the determination of stresses at every point (material particle) in the object. According to Cauchy, the stress at any point in an object (Figure 2), assumed as a continuum, is completely defined by the nine stress components [math]\displaystyle{ \sigma_{ij} }[/math] of a second order tensor of type (2,0) known as the Cauchy stress tensor, [math]\displaystyle{ \boldsymbol\sigma }[/math]:

[math]\displaystyle{ \boldsymbol{\sigma}= \left[{\begin{matrix} \sigma _{11} & \sigma _{12} & \sigma _{13} \\ \sigma _{21} & \sigma _{22} & \sigma _{23} \\ \sigma _{31} & \sigma _{32} & \sigma _{33} \\ \end{matrix}}\right] \equiv \left[{\begin{matrix} \sigma _{xx} & \sigma _{xy} & \sigma _{xz} \\ \sigma _{yx} & \sigma _{yy} & \sigma _{yz} \\ \sigma _{zx} & \sigma _{zy} & \sigma _{zz} \\ \end{matrix}}\right] \equiv \left[{\begin{matrix} \sigma _x & \tau _{xy} & \tau _{xz} \\ \tau _{yx} & \sigma _y & \tau _{yz} \\ \tau _{zx} & \tau _{zy} & \sigma _z \\ \end{matrix}}\right] }[/math]

Figure 3. Stress transformation at a point in a continuum under plane stress conditions.

After the stress distribution within the object has been determined with respect to a coordinate system [math]\displaystyle{ (x,y) }[/math], it may be necessary to calculate the components of the stress tensor at a particular material point [math]\displaystyle{ P }[/math] with respect to a rotated coordinate system [math]\displaystyle{ (x',y') }[/math], i.e., the stresses acting on a plane with a different orientation passing through that point of interest —forming an angle with the coordinate system [math]\displaystyle{ (x,y) }[/math] (Figure 3). For example, it is of interest to find the maximum normal stress and maximum shear stress, as well as the orientation of the planes where they act upon. To achieve this, it is necessary to perform a tensor transformation under a rotation of the coordinate system. From the definition of tensor, the Cauchy stress tensor obeys the tensor transformation law. A graphical representation of this transformation law for the Cauchy stress tensor is the Mohr circle for stress.

Mohr's circle for two-dimensional state of stress

Figure 4. Stress components at a plane passing through a point in a continuum under plane stress conditions.

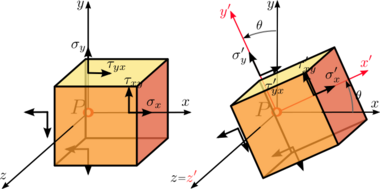
In two dimensions, the stress tensor at a given material point [math]\displaystyle{ P }[/math] with respect to any two perpendicular directions is completely defined by only three stress components. For the particular coordinate system [math]\displaystyle{ (x,y) }[/math] these stress components are: the normal stresses [math]\displaystyle{ \sigma_x }[/math] and [math]\displaystyle{ \sigma_y }[/math], and the shear stress [math]\displaystyle{ \tau_{xy} }[/math]. From the balance of angular momentum, the symmetry of the Cauchy stress tensor can be demonstrated. This symmetry implies that [math]\displaystyle{ \tau_{xy}=\tau_{yx} }[/math]. Thus, the Cauchy stress tensor can be written as:

[math]\displaystyle{ \boldsymbol{\sigma}= \left[{\begin{matrix} \sigma _x & \tau _{xy} & 0 \\ \tau _{xy} & \sigma _y & 0 \\ 0 & 0 & 0 \\ \end{matrix}}\right] \equiv \left[{\begin{matrix} \sigma _x & \tau _{xy} \\ \tau _{xy} & \sigma _y \\ \end{matrix}}\right] }[/math]

The objective is to use the Mohr circle to find the stress components [math]\displaystyle{ \sigma_\mathrm{n} }[/math] and [math]\displaystyle{ \tau_\mathrm{n} }[/math] on a rotated coordinate system [math]\displaystyle{ (x',y') }[/math], i.e., on a differently oriented plane passing through [math]\displaystyle{ P }[/math] and perpendicular to the [math]\displaystyle{ x }[/math]-[math]\displaystyle{ y }[/math] plane (Figure 4). The rotated coordinate system [math]\displaystyle{ (x',y') }[/math] makes an angle [math]\displaystyle{ \theta }[/math] with the original coordinate system [math]\displaystyle{ (x,y) }[/math].

Equation of the Mohr circle

To derive the equation of the Mohr circle for the two-dimensional cases of plane stress and plane strain, first consider a two-dimensional infinitesimal material element around a material point [math]\displaystyle{ P }[/math] (Figure 4), with a unit area in the direction parallel to the [math]\displaystyle{ y }[/math]-[math]\displaystyle{ z }[/math] plane, i.e., perpendicular to the page or screen.

From equilibrium of forces on the infinitesimal element, the magnitudes of the normal stress [math]\displaystyle{ \sigma_\mathrm{n} }[/math] and the shear stress [math]\displaystyle{ \tau_\mathrm{n} }[/math] are given by:

[math]\displaystyle{ \sigma_\mathrm{n} = \frac{1}{2} ( \sigma_x + \sigma_y ) + \frac{1}{2} ( \sigma_x - \sigma_y )\cos 2\theta + \tau_{xy} \sin 2\theta }[/math]

[math]\displaystyle{ \tau_\mathrm{n} = -\frac{1}{2}(\sigma_x - \sigma_y )\sin 2\theta + \tau_{xy}\cos 2\theta }[/math]

Derivation of Mohr's circle parametric equations - Equilibrium of forces

From equilibrium of forces in the direction of [math]\displaystyle{ \sigma_\mathrm{n} }[/math] ([math]\displaystyle{ x' }[/math]-axis) (Figure 4), and knowing that the area of the plane where [math]\displaystyle{ \sigma_\mathrm{n} }[/math] acts is [math]\displaystyle{ dA }[/math], we have: [math]\displaystyle{ \ \begin{align} \sum F_{x'} &= \sigma_\mathrm{n} dA - \sigma_x dA \cos ^2 \theta - \sigma_y dA \sin ^2 \theta - \tau_{xy} dA \cos \theta \sin \theta - \tau_{xy} dA \sin \theta \cos \theta = 0 \\ \sigma_\mathrm{n} &= \sigma_x \cos ^2 \theta + \sigma_y \sin ^2 \theta + 2\tau_{xy} \sin \theta \cos \theta \\ \end{align} }[/math] However, knowing that [math]\displaystyle{ \cos ^2 \theta = \frac{1+\cos 2\theta}{2}, \qquad \sin ^2 \theta = \frac{1-\cos 2\theta}{2} \qquad \text{and} \qquad \sin 2\theta= 2\sin\theta\cos\theta }[/math] we obtain [math]\displaystyle{ \sigma_\mathrm{n} = \frac{1}{2} ( \sigma_x + \sigma_y ) + \frac{1}{2} ( \sigma_x - \sigma_y )\cos 2\theta + \tau_{xy} \sin 2\theta }[/math] Now, from equilibrium of forces in the direction of [math]\displaystyle{ \tau_\mathrm{n} }[/math] ([math]\displaystyle{ y' }[/math]-axis) (Figure 4), and knowing that the area of the plane where [math]\displaystyle{ \tau_\mathrm{n} }[/math] acts is [math]\displaystyle{ dA }[/math], we have: [math]\displaystyle{ \ \begin{align} \sum F_{y'} &= \tau_\mathrm{n} dA + \sigma_x dA \cos \theta \sin \theta - \sigma_y dA \sin \theta \cos \theta - \tau_{xy} dA \cos ^2 \theta + \tau_{xy} dA \sin ^2 \theta = 0 \\ \tau_\mathrm{n} &= -(\sigma_x-\sigma_y) \sin\theta\cos\theta + \tau_{xy} \left( \cos^2 \theta -\sin^2 \theta \right) \\ \end{align} }[/math] However, knowing that [math]\displaystyle{ \cos ^2 \theta - \sin^2\theta=\cos 2\theta \qquad \text{and} \qquad \sin 2\theta= 2\sin\theta\cos\theta }[/math] we obtain [math]\displaystyle{ \tau_\mathrm{n} = -\frac{1}{2}(\sigma_x - \sigma_y )\sin 2\theta + \tau_{xy}\cos 2\theta }[/math]

Both equations can also be obtained by applying the tensor transformation law on the known Cauchy stress tensor, which is equivalent to performing the static equilibrium of forces in the direction of [math]\displaystyle{ \sigma_\mathrm{n} }[/math] and [math]\displaystyle{ \tau_\mathrm{n} }[/math].

Derivation of Mohr's circle parametric equations - Tensor transformation

The stress tensor transformation law can be stated as [math]\displaystyle{ \begin{align} \boldsymbol{\sigma}' &= \mathbf A \boldsymbol{\sigma} \mathbf A^T \\ \left[{\begin{matrix} \sigma_{x'} & \tau_{x'y'} \\ \tau_{y'x'} & \sigma_{y'} \\ \end{matrix}}\right] &=\left[{\begin{matrix} a_{x} & a_{xy} \\ a_{yx} & a_{y} \\ \end{matrix}}\right] \left[{\begin{matrix} \sigma_{x} & \tau_{xy} \\ \tau_{yx} & \sigma_{y} \\ \end{matrix}}\right]\left[{\begin{matrix} a_{x} & a_{yx} \\ a_{xy} & a_{y} \\ \end{matrix}}\right] \\ &= \left[{\begin{matrix} \cos\theta & \sin\theta \\ -\sin\theta & \cos\theta \\ \end{matrix}}\right]\left[{\begin{matrix} \sigma_{x} & \tau_{xy} \\ \tau_{yx} & \sigma_{y} \\ \end{matrix}}\right] \left[{\begin{matrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \\ \end{matrix}}\right] \end{align} }[/math] Expanding the right hand side, and knowing that [math]\displaystyle{ \sigma_{x'}=\sigma_\mathrm{n} }[/math] and [math]\displaystyle{ \tau_{x'y'}=\tau_\mathrm{n} }[/math], we have: [math]\displaystyle{ \sigma_\mathrm{n} = \sigma_x \cos ^2 \theta + \sigma_y \sin ^2 \theta + 2\tau_{xy} \sin \theta \cos \theta }[/math] However, knowing that [math]\displaystyle{ \cos ^2 \theta = \frac{1+\cos 2\theta}{2}, \qquad \sin ^2 \theta = \frac{1-\cos 2\theta}{2} \qquad \text{and} \qquad \sin 2\theta= 2\sin\theta\cos\theta }[/math] we obtain [math]\displaystyle{ \sigma_\mathrm{n} = \frac{1}{2} ( \sigma_x + \sigma_y ) + \frac{1}{2} ( \sigma_x - \sigma_y )\cos 2\theta + \tau_{xy} \sin 2\theta }[/math] [math]\displaystyle{ \tau_\mathrm{n} = -(\sigma_x-\sigma_y) \sin\theta\cos\theta + \tau_{xy} \left( \cos^2 \theta -\sin^2 \theta \right) }[/math] However, knowing that [math]\displaystyle{ \cos ^2 \theta - \sin^2\theta=\cos 2\theta \qquad \text{and} \qquad \sin 2\theta= 2\sin\theta\cos\theta }[/math] we obtain [math]\displaystyle{ \tau_\mathrm{n} = -\frac{1}{2}(\sigma_x - \sigma_y )\sin 2\theta + \tau_{xy}\cos 2\theta }[/math] It is not necessary at this moment to calculate the stress component [math]\displaystyle{ \sigma_{y'} }[/math] acting on the plane perpendicular to the plane of action of [math]\displaystyle{ \sigma_{x'} }[/math] as it is not required for deriving the equation for the Mohr circle.

These two equations are the parametric equations of the Mohr circle. In these equations, [math]\displaystyle{ 2\theta }[/math] is the parameter, and [math]\displaystyle{ \sigma_\mathrm{n} }[/math] and [math]\displaystyle{ \tau_\mathrm{n} }[/math] are the coordinates. This means that by choosing a coordinate system with abscissa [math]\displaystyle{ \sigma_\mathrm{n} }[/math] and ordinate [math]\displaystyle{ \tau_\mathrm{n} }[/math], giving values to the parameter [math]\displaystyle{ \theta }[/math] will place the points obtained lying on a circle.

Eliminating the parameter [math]\displaystyle{ 2\theta }[/math] from these parametric equations will yield the non-parametric equation of the Mohr circle. This can be achieved by rearranging the equations for [math]\displaystyle{ \sigma_\mathrm{n} }[/math] and [math]\displaystyle{ \tau_\mathrm{n} }[/math], first transposing the first term in the first equation and squaring both sides of each of the equations then adding them. Thus we have

[math]\displaystyle{ \begin{align} \left[ \sigma_\mathrm{n} - \tfrac{1}{2} ( \sigma_x + \sigma_y )\right]^2 + \tau_\mathrm{n}^2 &= \left[\tfrac{1}{2}(\sigma_x - \sigma_y)\right]^2 + \tau_{xy}^2 \\ (\sigma_\mathrm{n} - \sigma_\mathrm{avg})^2 + \tau_\mathrm{n}^2 &= R^2 \end{align} }[/math]

where

[math]\displaystyle{ R = \sqrt{\left[\tfrac{1}{2}(\sigma_x - \sigma_y)\right]^2 + \tau_{xy}^2} \quad \text{and} \quad \sigma_\mathrm{avg} = \tfrac{1}{2} ( \sigma_x + \sigma_y ) }[/math]

This is the equation of a circle (the Mohr circle) of the form

[math]\displaystyle{ (x-a)^2+(y-b)^2=r^2 }[/math]

with radius [math]\displaystyle{ r=R }[/math] centered at a point with coordinates [math]\displaystyle{ (a,b)=(\sigma_\mathrm{avg}, 0) }[/math] in the [math]\displaystyle{ (\sigma_\mathrm{n},\tau_\mathrm{n}) }[/math] coordinate system.

Sign conventions

There are two separate sets of sign conventions that need to be considered when using the Mohr Circle: One sign convention for stress components in the "physical space", and another for stress components in the "Mohr-Circle-space". In addition, within each of the two set of sign conventions, the engineering mechanics (structural engineering and mechanical engineering) literature follows a different sign convention from the geomechanics literature. There is no standard sign convention, and the choice of a particular sign convention is influenced by convenience for calculation and interpretation for the particular problem in hand. A more detailed explanation of these sign conventions is presented below.

The previous derivation for the equation of the Mohr Circle using Figure 4 follows the engineering mechanics sign convention. The engineering mechanics sign convention will be used for this article.

Physical-space sign convention

From the convention of the Cauchy stress tensor (Figure 3 and Figure 4), the first subscript in the stress components denotes the face on which the stress component acts, and the second subscript indicates the direction of the stress component. Thus [math]\displaystyle{ \tau_{xy} }[/math] is the shear stress acting on the face with normal vector in the positive direction of the [math]\displaystyle{ x }[/math]-axis, and in the positive direction of the [math]\displaystyle{ y }[/math]-axis.

In the physical-space sign convention, positive normal stresses are outward to the plane of action (tension), and negative normal stresses are inward to the plane of action (compression) (Figure 5).

In the physical-space sign convention, positive shear stresses act on positive faces of the material element in the positive direction of an axis. Also, positive shear stresses act on negative faces of the material element in the negative direction of an axis. A positive face has its normal vector in the positive direction of an axis, and a negative face has its normal vector in the negative direction of an axis. For example, the shear stresses [math]\displaystyle{ \tau_{xy} }[/math] and [math]\displaystyle{ \tau_{yx} }[/math] are positive because they act on positive faces, and they act as well in the positive direction of the [math]\displaystyle{ y }[/math]-axis and the [math]\displaystyle{ x }[/math]-axis, respectively (Figure 3). Similarly, the respective opposite shear stresses [math]\displaystyle{ \tau_{xy} }[/math] and [math]\displaystyle{ \tau_{yx} }[/math] acting in the negative faces have a negative sign because they act in the negative direction of the [math]\displaystyle{ x }[/math]-axis and [math]\displaystyle{ y }[/math]-axis, respectively.

Mohr-circle-space sign convention

Figure 5. Engineering mechanics sign convention for drawing the Mohr circle. This article follows sign-convention # 3, as shown.

In the Mohr-circle-space sign convention, normal stresses have the same sign as normal stresses in the physical-space sign convention: positive normal stresses act outward to the plane of action, and negative normal stresses act inward to the plane of action.

Shear stresses, however, have a different convention in the Mohr-circle space compared to the convention in the physical space. In the Mohr-circle-space sign convention, positive shear stresses rotate the material element in the counterclockwise direction, and negative shear stresses rotate the material in the clockwise direction. This way, the shear stress component [math]\displaystyle{ \tau_{xy} }[/math] is positive in the Mohr-circle space, and the shear stress component [math]\displaystyle{ \tau_{yx} }[/math] is negative in the Mohr-circle space.

Two options exist for drawing the Mohr-circle space, which produce a mathematically correct Mohr circle:

1. Positive shear stresses are plotted upward (Figure 5, sign convention #1)
2. Positive shear stresses are plotted downward, i.e., the [math]\displaystyle{ \tau_\mathrm n }[/math]-axis is inverted (Figure 5, sign convention #2).

Plotting positive shear stresses upward makes the angle [math]\displaystyle{ 2\theta }[/math] on the Mohr circle have a positive rotation clockwise, which is opposite to the physical space convention. That is why some authors prefer plotting positive shear stresses downward, which makes the angle [math]\displaystyle{ 2\theta }[/math] on the Mohr circle have a positive rotation counterclockwise, similar to the physical space convention for shear stresses.

To overcome the "issue" of having the shear stress axis downward in the Mohr-circle space, there is an alternative sign convention where positive shear stresses are assumed to rotate the material element in the clockwise direction and negative shear stresses are assumed to rotate the material element in the counterclockwise direction (Figure 5, option 3). This way, positive shear stresses are plotted upward in the Mohr-circle space and the angle [math]\displaystyle{ 2\theta }[/math] has a positive rotation counterclockwise in the Mohr-circle space. This alternative sign convention produces a circle that is identical to the sign convention #2 in Figure 5 because a positive shear stress [math]\displaystyle{ \tau_\mathrm n }[/math] is also a counterclockwise shear stress, and both are plotted downward. Also, a negative shear stress [math]\displaystyle{ \tau_\mathrm n }[/math] is a clockwise shear stress, and both are plotted upward.

This article follows the engineering mechanics sign convention for the physical space and the alternative sign convention for the Mohr-circle space (sign convention #3 in Figure 5)

Drawing Mohr's circle

Figure 6. Mohr's circle for plane stress and plane strain conditions (double angle approach). After a stress analysis, the stress components [math]\displaystyle{ \sigma_x }[/math], [math]\displaystyle{ \sigma_y }[/math], and [math]\displaystyle{ \tau_{xy} }[/math] at a material point [math]\displaystyle{ P }[/math] are known. These stress components act on two perpendicular planes [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math] passing through [math]\displaystyle{ P }[/math]. The coordinates of point [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math] on the Mohr circle are the stress components acting on the planes [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math] of the material element, respectively. The Mohr circle is then used to find the stress components [math]\displaystyle{ \sigma_\mathrm{n} }[/math] and [math]\displaystyle{ \tau_\mathrm{n} }[/math], i.e., coordinates of any stress point [math]\displaystyle{ D }[/math] on the circle, acting on any other plane [math]\displaystyle{ D }[/math] passing through [math]\displaystyle{ P }[/math]. The angle between the lines [math]\displaystyle{ \overline {OB} }[/math] and [math]\displaystyle{ \overline {OD} }[/math] is double the angle [math]\displaystyle{ \theta }[/math] between the normal vectors of planes [math]\displaystyle{ B }[/math] and [math]\displaystyle{ D }[/math] passing through [math]\displaystyle{ P }[/math].

Assuming we know the stress components [math]\displaystyle{ \sigma_x }[/math], [math]\displaystyle{ \sigma_y }[/math], and [math]\displaystyle{ \tau_{xy} }[/math] at a point [math]\displaystyle{ P }[/math] in the object under study, as shown in Figure 4, the following are the steps to construct the Mohr circle for the state of stresses at [math]\displaystyle{ P }[/math]:

1. Draw the Cartesian coordinate system [math]\displaystyle{ (\sigma_\mathrm{n},\tau_\mathrm{n}) }[/math] with a horizontal [math]\displaystyle{ \sigma_\mathrm{n} }[/math]-axis and a vertical [math]\displaystyle{ \tau_\mathrm{n} }[/math]-axis.
2. Plot two points [math]\displaystyle{ A(\sigma_y, \tau_{xy}) }[/math] and [math]\displaystyle{ B(\sigma_x, -\tau_{xy}) }[/math] in the [math]\displaystyle{ (\sigma_\mathrm{n},\tau_\mathrm{n}) }[/math] space corresponding to the known stress components on both perpendicular planes [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math], respectively (Figure 4 and 6), following the chosen sign convention.
3. Draw the diameter of the circle by joining points [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math] with a straight line [math]\displaystyle{ \overline{AB} }[/math].
4. Draw the Mohr Circle. The centre [math]\displaystyle{ O }[/math] of the circle is the midpoint of the diameter line [math]\displaystyle{ \overline{AB} }[/math], which corresponds to the intersection of this line with the [math]\displaystyle{ \sigma_\mathrm{n} }[/math] axis.

Finding principal normal stresses

Stress components on a 2D rotating element. Click to see animation. Example of how stress components vary on the faces (edges) of a rectangular element as the angle of its orientation is varied. Principal stresses occur when the shear stresses simultaneously disappear from all faces. The orientation at which this occurs gives the principal directions. In this example, when the rectangle is horizontal, the stresses are given by [math]\displaystyle{ \left[{\begin{matrix} \sigma_{xx} & \tau_{xy}\\ \tau_{yx} & \sigma_{yy} \end{matrix}}\right] = \left[\begin{matrix} -10 & 10\\ 10 & 15\end{matrix}\right]. }[/math] The corresponding Mohr's circle representation is shown at the bottom.

The magnitude of the principal stresses are the abscissas of the points [math]\displaystyle{ C }[/math] and [math]\displaystyle{ E }[/math] (Figure 6) where the circle intersects the [math]\displaystyle{ \sigma_\mathrm n }[/math]-axis. The magnitude of the major principal stress [math]\displaystyle{ \sigma_1 }[/math] is always the greatest absolute value of the abscissa of any of these two points. Likewise, the magnitude of the minor principal stress [math]\displaystyle{ \sigma_2 }[/math] is always the lowest absolute value of the abscissa of these two points. As expected, the ordinates of these two points are zero, corresponding to the magnitude of the shear stress components on the principal planes. Alternatively, the values of the principal stresses can be found by

[math]\displaystyle{ \sigma_1 = \sigma_\max = \sigma_\text{avg}+R }[/math]

[math]\displaystyle{ \sigma_2 = \sigma_\min = \sigma_\text{avg}-R }[/math]

where the magnitude of the average normal stress [math]\displaystyle{ \sigma_\text{avg} }[/math] is the abscissa of the centre [math]\displaystyle{ O }[/math], given by

[math]\displaystyle{ \sigma_\text{avg} = \tfrac{1}{2}(\sigma_x+ \sigma_y) }[/math]

and the length of the radius [math]\displaystyle{ R }[/math] of the circle (based on the equation of a circle passing through two points), is given by

[math]\displaystyle{ R = \sqrt{\left[\tfrac{1}{2}(\sigma_x - \sigma_y)\right]^2 + \tau_{xy}^2} }[/math]

Finding maximum and minimum shear stresses

The maximum and minimum shear stresses correspond to the ordinates of the highest and lowest points on the circle, respectively. These points are located at the intersection of the circle with the vertical line passing through the center of the circle, [math]\displaystyle{ O }[/math]. Thus, the magnitude of the maximum and minimum shear stresses are equal to the value of the circle's radius [math]\displaystyle{ R }[/math]

[math]\displaystyle{ \tau_{\max,\min}= \pm R }[/math]

Finding stress components on an arbitrary plane

As mentioned before, after the two-dimensional stress analysis has been performed we know the stress components [math]\displaystyle{ \sigma_x }[/math], [math]\displaystyle{ \sigma_y }[/math], and [math]\displaystyle{ \tau_{xy} }[/math] at a material point [math]\displaystyle{ P }[/math]. These stress components act in two perpendicular planes [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math] passing through [math]\displaystyle{ P }[/math] as shown in Figure 5 and 6. The Mohr circle is used to find the stress components [math]\displaystyle{ \sigma_\mathrm{n} }[/math] and [math]\displaystyle{ \tau_\mathrm{n} }[/math], i.e., coordinates of any point [math]\displaystyle{ D }[/math] on the circle, acting on any other plane [math]\displaystyle{ D }[/math] passing through [math]\displaystyle{ P }[/math] making an angle [math]\displaystyle{ \theta }[/math] with the plane [math]\displaystyle{ B }[/math]. For this, two approaches can be used: the double angle, and the Pole or origin of planes.

Double angle

As shown in Figure 6, to determine the stress components [math]\displaystyle{ (\sigma_\mathrm{n}, \tau_\mathrm{n}) }[/math] acting on a plane [math]\displaystyle{ D }[/math] at an angle [math]\displaystyle{ \theta }[/math] counterclockwise to the plane [math]\displaystyle{ B }[/math] on which [math]\displaystyle{ \sigma_x }[/math] acts, we travel an angle [math]\displaystyle{ 2\theta }[/math] in the same counterclockwise direction around the circle from the known stress point [math]\displaystyle{ B(\sigma_x, -\tau_{xy}) }[/math] to point [math]\displaystyle{ D(\sigma_\mathrm{n}, \tau_\mathrm{n}) }[/math], i.e., an angle [math]\displaystyle{ 2\theta }[/math] between lines [math]\displaystyle{ \overline {OB} }[/math] and [math]\displaystyle{ \overline {OD} }[/math] in the Mohr circle.

The double angle approach relies on the fact that the angle [math]\displaystyle{ \theta }[/math] between the normal vectors to any two physical planes passing through [math]\displaystyle{ P }[/math] (Figure 4) is half the angle between two lines joining their corresponding stress points [math]\displaystyle{ (\sigma_\mathrm{n}, \tau_\mathrm{n}) }[/math] on the Mohr circle and the centre of the circle.

This double angle relation comes from the fact that the parametric equations for the Mohr circle are a function of [math]\displaystyle{ 2\theta }[/math]. It can also be seen that the planes [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math] in the material element around [math]\displaystyle{ P }[/math] of Figure 5 are separated by an angle [math]\displaystyle{ \theta=90^\circ }[/math], which in the Mohr circle is represented by a [math]\displaystyle{ 180^\circ }[/math] angle (double the angle).

Pole or origin of planes

Figure 7. Mohr's circle for plane stress and plane strain conditions (Pole approach). Any straight line drawn from the pole will intersect the Mohr circle at a point that represents the state of stress on a plane inclined at the same orientation (parallel) in space as that line.

The second approach involves the determination of a point on the Mohr circle called the pole or the origin of planes. Any straight line drawn from the pole will intersect the Mohr circle at a point that represents the state of stress on a plane inclined at the same orientation (parallel) in space as that line. Therefore, knowing the stress components [math]\displaystyle{ \sigma }[/math] and [math]\displaystyle{ \tau }[/math] on any particular plane, one can draw a line parallel to that plane through the particular coordinates [math]\displaystyle{ \sigma_\mathrm{n} }[/math] and [math]\displaystyle{ \tau_\mathrm{n} }[/math] on the Mohr circle and find the pole as the intersection of such line with the Mohr circle. As an example, let's assume we have a state of stress with stress components [math]\displaystyle{ \sigma_x,\! }[/math], [math]\displaystyle{ \sigma_y,\! }[/math], and [math]\displaystyle{ \tau_{xy},\! }[/math], as shown on Figure 7. First, we can draw a line from point [math]\displaystyle{ B }[/math] parallel to the plane of action of [math]\displaystyle{ \sigma_x }[/math], or, if we choose otherwise, a line from point [math]\displaystyle{ A }[/math] parallel to the plane of action of [math]\displaystyle{ \sigma_y }[/math]. The intersection of any of these two lines with the Mohr circle is the pole. Once the pole has been determined, to find the state of stress on a plane making an angle [math]\displaystyle{ \theta }[/math] with the vertical, or in other words a plane having its normal vector forming an angle [math]\displaystyle{ \theta }[/math] with the horizontal plane, then we can draw a line from the pole parallel to that plane (See Figure 7). The normal and shear stresses on that plane are then the coordinates of the point of intersection between the line and the Mohr circle.

Finding the orientation of the principal planes

The orientation of the planes where the maximum and minimum principal stresses act, also known as principal planes, can be determined by measuring in the Mohr circle the angles ∠BOC and ∠BOE, respectively, and taking half of each of those angles. Thus, the angle ∠BOC between [math]\displaystyle{ \overline{OB} }[/math] and [math]\displaystyle{ \overline{OC} }[/math] is double the angle [math]\displaystyle{ \theta_p }[/math] which the major principal plane makes with plane [math]\displaystyle{ B }[/math].

Angles [math]\displaystyle{ \theta_{p1} }[/math] and [math]\displaystyle{ \theta_{p2} }[/math] can also be found from the following equation

[math]\displaystyle{ \tan 2 \theta_\mathrm{p} = \frac{2 \tau_{xy}}{\sigma_y - \sigma_x} }[/math]

This equation defines two values for [math]\displaystyle{ \theta_\mathrm{p} }[/math] which are [math]\displaystyle{ 90^\circ }[/math] apart (Figure). This equation can be derived directly from the geometry of the circle, or by making the parametric equation of the circle for [math]\displaystyle{ \tau_\mathrm n }[/math] equal to zero (the shear stress in the principal planes is always zero).

Example

Figure 8

Figure 9

Assume a material element under a state of stress as shown in Figure 8 and Figure 9, with the plane of one of its sides oriented 10° with respect to the horizontal plane. Using the Mohr circle, find:

• The orientation of their planes of action.
• The maximum shear stresses and orientation of their planes of action.
• The stress components on a horizontal plane.

Check the answers using the stress transformation formulas or the stress transformation law.

Solution: Following the engineering mechanics sign convention for the physical space (Figure 5), the stress components for the material element in this example are:

[math]\displaystyle{ \sigma_{x'}=-10\textrm{ MPa} }[/math]

[math]\displaystyle{ \sigma_{y'}=50\textrm{ MPa} }[/math]

[math]\displaystyle{ \tau_{x'y'}=40\textrm{ MPa} }[/math].

Following the steps for drawing the Mohr circle for this particular state of stress, we first draw a Cartesian coordinate system [math]\displaystyle{ (\sigma_\mathrm{n},\tau_\mathrm{n}) }[/math] with the [math]\displaystyle{ \tau_\mathrm{n} }[/math]-axis upward.

We then plot two points A(50,40) and B(-10,-40), representing the state of stress at plane A and B as show in both Figure 8 and Figure 9. These points follow the engineering mechanics sign convention for the Mohr-circle space (Figure 5), which assumes positive normals stresses outward from the material element, and positive shear stresses on each plane rotating the material element clockwise. This way, the shear stress acting on plane B is negative and the shear stress acting on plane A is positive. The diameter of the circle is the line joining point A and B. The centre of the circle is the intersection of this line with the [math]\displaystyle{ \sigma_\mathrm{n} }[/math]-axis. Knowing both the location of the centre and length of the diameter, we are able to plot the Mohr circle for this particular state of stress.

The abscissas of both points E and C (Figure 8 and Figure 9) intersecting the [math]\displaystyle{ \sigma_\mathrm{n} }[/math]-axis are the magnitudes of the minimum and maximum normal stresses, respectively; the ordinates of both points E and C are the magnitudes of the shear stresses acting on both the minor and major principal planes, respectively, which is zero for principal planes.

Even though the idea for using the Mohr circle is to graphically find different stress components by actually measuring the coordinates for different points on the circle, it is more convenient to confirm the results analytically. Thus, the radius and the abscissa of the centre of the circle are

[math]\displaystyle{ \begin{align} R &= \sqrt{\left[\tfrac{1}{2}(\sigma_x - \sigma_y)\right]^2 + \tau_{xy}^2} \\ &= \sqrt{\left[\tfrac{1}{2}(-10 - 50)\right]^2 + 40^2} \\ &= 50 \textrm{ MPa} \\ \end{align} }[/math]

[math]\displaystyle{ \begin{align} \sigma_\mathrm{avg} &= \tfrac{1}{2}(\sigma_x + \sigma_y) \\ &= \tfrac{1}{2}(-10 + 50) \\ &= 20 \textrm{ MPa} \\ \end{align} }[/math]

and the principal stresses are

[math]\displaystyle{ \begin{align} \sigma_1 &= \sigma_\mathrm{avg}+R \\ &= 70 \textrm{ MPa} \\ \end{align} }[/math]

[math]\displaystyle{ \begin{align} \sigma_2 &= \sigma_\mathrm{avg}-R \\ &= -30 \textrm{ MPa} \\ \end{align} }[/math]

The coordinates for both points H and G (Figure 8 and Figure 9) are the magnitudes of the minimum and maximum shear stresses, respectively; the abscissas for both points H and G are the magnitudes for the normal stresses acting on the same planes where the minimum and maximum shear stresses act, respectively. The magnitudes of the minimum and maximum shear stresses can be found analytically by

[math]\displaystyle{ \tau_{\max,\min}= \pm R = \pm 50 \textrm{ MPa} }[/math]

and the normal stresses acting on the same planes where the minimum and maximum shear stresses act are equal to [math]\displaystyle{ \sigma_\mathrm{avg} }[/math]

We can choose to either use the double angle approach (Figure 8) or the Pole approach (Figure 9) to find the orientation of the principal normal stresses and principal shear stresses.

Using the double angle approach we measure the angles ∠BOC and ∠BOE in the Mohr Circle (Figure 8) to find double the angle the major principal stress and the minor principal stress make with plane B in the physical space. To obtain a more accurate value for these angles, instead of manually measuring the angles, we can use the analytical expression

[math]\displaystyle{ \begin{align} 2 \theta_\mathrm{p} = \arctan\frac{2 \tau_{xy}}{\sigma_x - \sigma_y}=\arctan\frac{2*40}{(-10-50)}=-\arctan\frac{4}{3} \end{align} }[/math]

One solution is: [math]\displaystyle{ 2\theta_{p}=-53.13^\circ }[/math]. From inspection of Figure 8, this value corresponds to the angle ∠BOE. Thus, the minor principal angle is

[math]\displaystyle{ \theta_{p2}=-26.565^\circ }[/math]

Then, the major principal angle is

[math]\displaystyle{ \begin{align} 2\theta_{p1}&=180-53.13^\circ=126.87^\circ \\ \theta_{p1}&=63.435^\circ \\ \end{align} }[/math]

Remember that in this particular example [math]\displaystyle{ \theta_{p1} }[/math] and [math]\displaystyle{ \theta_{p2} }[/math] are angles with respect to the plane of action of [math]\displaystyle{ \sigma_{x'} }[/math] (oriented in the [math]\displaystyle{ x' }[/math]-axis)and not angles with respect to the plane of action of [math]\displaystyle{ \sigma_x }[/math] (oriented in the [math]\displaystyle{ x }[/math]-axis).

Using the Pole approach, we first localize the Pole or origin of planes. For this, we draw through point A on the Mohr circle a line inclined 10° with the horizontal, or, in other words, a line parallel to plane A where [math]\displaystyle{ \sigma_{y'} }[/math] acts. The Pole is where this line intersects the Mohr circle (Figure 9). To confirm the location of the Pole, we could draw a line through point B on the Mohr circle parallel to the plane B where [math]\displaystyle{ \sigma_{x'} }[/math] acts. This line would also intersect the Mohr circle at the Pole (Figure 9).

From the Pole, we draw lines to different points on the Mohr circle. The coordinates of the points where these lines intersect the Mohr circle indicate the stress components acting on a plane in the physical space having the same inclination as the line. For instance, the line from the Pole to point C in the circle has the same inclination as the plane in the physical space where [math]\displaystyle{ \sigma_1 }[/math] acts. This plane makes an angle of 63.435° with plane B, both in the Mohr-circle space and in the physical space. In the same way, lines are traced from the Pole to points E, D, F, G and H to find the stress components on planes with the same orientation.

Mohr's circle for a general three-dimensional state of stresses

Figure 10. Mohr's circle for a three-dimensional state of stress

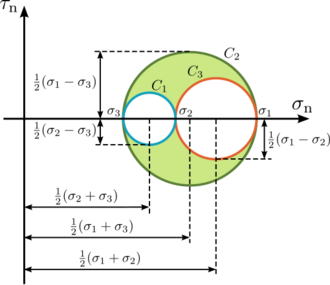
To construct the Mohr circle for a general three-dimensional case of stresses at a point, the values of the principal stresses [math]\displaystyle{ \left(\sigma_1, \sigma_2, \sigma_3 \right) }[/math] and their principal directions [math]\displaystyle{ \left(n_1, n_2, n_3 \right) }[/math] must be first evaluated.

Considering the principal axes as the coordinate system, instead of the general [math]\displaystyle{ x_1 }[/math], [math]\displaystyle{ x_2 }[/math], [math]\displaystyle{ x_3 }[/math] coordinate system, and assuming that [math]\displaystyle{ \sigma_1 \gt \sigma_2 \gt \sigma_3 }[/math], then the normal and shear components of the stress vector [math]\displaystyle{ \mathbf T^{(\mathbf n)} }[/math], for a given plane with unit vector [math]\displaystyle{ \mathbf n }[/math], satisfy the following equations

[math]\displaystyle{ \begin{align} \left( T^{(n)} \right)^2 &= \sigma_{ij}\sigma_{ik}n_jn_k \\ \sigma_\mathrm{n}^2 + \tau_\mathrm{n}^2 &= \sigma_1^2 n_1^2 + \sigma_2^2 n_2^2 + \sigma_3^2 n_3^2 \end{align} }[/math]

[math]\displaystyle{ \sigma_\mathrm{n} = \sigma_1 n_1^2 + \sigma_2 n_2^2 + \sigma_3 n_3^2. }[/math]

Knowing that [math]\displaystyle{ n_i n_i = n_1^2+n_2^2+n_3^2 = 1 }[/math], we can solve for [math]\displaystyle{ n_1^2 }[/math], [math]\displaystyle{ n_2^2 }[/math], [math]\displaystyle{ n_3^2 }[/math], using the Gauss elimination method which yields

[math]\displaystyle{ \begin{align} n_1^2 &= \frac{\tau_\mathrm{n}^2+(\sigma_\mathrm{n} - \sigma_2)(\sigma_\mathrm{n} - \sigma_3)}{(\sigma_1 - \sigma_2)(\sigma_1 - \sigma_3)} \ge 0\\ n_2^2 &= \frac{\tau_\mathrm{n}^2+(\sigma_\mathrm{n} - \sigma_3)(\sigma_\mathrm{n} - \sigma_1)}{(\sigma_2 - \sigma_3)(\sigma_2 - \sigma_1)} \ge 0\\ n_3^2 &= \frac{\tau_\mathrm{n}^2+(\sigma_\mathrm{n} - \sigma_1)(\sigma_\mathrm{n} - \sigma_2)}{(\sigma_3 - \sigma_1)(\sigma_3 - \sigma_2)} \ge 0. \end{align} }[/math]

Since [math]\displaystyle{ \sigma_1 \gt \sigma_2 \gt \sigma_3 }[/math], and [math]\displaystyle{ (n_i)^2 }[/math] is non-negative, the numerators from these equations satisfy

[math]\displaystyle{ \tau_\mathrm{n}^2+(\sigma_\mathrm{n} - \sigma_2)(\sigma_\mathrm{n} - \sigma_3) \ge 0 }[/math] as the denominator [math]\displaystyle{ \sigma_1 - \sigma_2 \gt 0 }[/math] and [math]\displaystyle{ \sigma_1 - \sigma_3 \gt 0 }[/math]

[math]\displaystyle{ \tau_\mathrm{n}^2+(\sigma_\mathrm{n} - \sigma_3)(\sigma_\mathrm{n} - \sigma_1) \le 0 }[/math] as the denominator [math]\displaystyle{ \sigma_2 - \sigma_3 \gt 0 }[/math] and [math]\displaystyle{ \sigma_2 - \sigma_1 \lt 0 }[/math]

[math]\displaystyle{ \tau_\mathrm{n}^2+(\sigma_\mathrm{n} - \sigma_1)(\sigma_\mathrm{n} - \sigma_2) \ge 0 }[/math] as the denominator [math]\displaystyle{ \sigma_3 - \sigma_1 \lt 0 }[/math] and [math]\displaystyle{ \sigma_3 - \sigma_2 \lt 0. }[/math]

These expressions can be rewritten as

[math]\displaystyle{ \begin{align} \tau_\mathrm{n}^2 + \left[ \sigma_\mathrm{n}- \tfrac{1}{2} (\sigma_2 + \sigma_3) \right]^2 \ge \left( \tfrac{1}{2}(\sigma_2 - \sigma_3) \right)^2 \\ \tau_\mathrm{n}^2 + \left[ \sigma_\mathrm{n}- \tfrac{1}{2} (\sigma_1 + \sigma_3) \right]^2 \le \left( \tfrac{1}{2}(\sigma_1 - \sigma_3) \right)^2 \\ \tau_\mathrm{n}^2 + \left[ \sigma_\mathrm{n}- \tfrac{1}{2} (\sigma_1 + \sigma_2) \right]^2 \ge \left( \tfrac{1}{2}(\sigma_1 - \sigma_2) \right)^2 \\ \end{align} }[/math]

which are the equations of the three Mohr's circles for stress [math]\displaystyle{ C_1 }[/math], [math]\displaystyle{ C_2 }[/math], and [math]\displaystyle{ C_3 }[/math], with radii [math]\displaystyle{ R_1=\tfrac{1}{2}(\sigma_2 - \sigma_3) }[/math], [math]\displaystyle{ R_2=\tfrac{1}{2}(\sigma_1 - \sigma_3) }[/math], and [math]\displaystyle{ R_3=\tfrac{1}{2}(\sigma_1 - \sigma_2) }[/math], and their centres with coordinates [math]\displaystyle{ \left[\tfrac{1}{2}(\sigma_2 + \sigma_3), 0\right] }[/math], [math]\displaystyle{ \left[\tfrac{1}{2}(\sigma_1 + \sigma_3), 0\right] }[/math], [math]\displaystyle{ \left[\tfrac{1}{2}(\sigma_1 + \sigma_2), 0\right] }[/math], respectively.

These equations for the Mohr circles show that all admissible stress points [math]\displaystyle{ (\sigma_\mathrm{n}, \tau_\mathrm{n}) }[/math] lie on these circles or within the shaded area enclosed by them (see Figure 10). Stress points [math]\displaystyle{ (\sigma_\mathrm{n}, \tau_\mathrm{n}) }[/math] satisfying the equation for circle [math]\displaystyle{ C_1 }[/math] lie on, or outside circle [math]\displaystyle{ C_1 }[/math]. Stress points [math]\displaystyle{ (\sigma_\mathrm{n}, \tau_\mathrm{n}) }[/math] satisfying the equation for circle [math]\displaystyle{ C_2 }[/math] lie on, or inside circle [math]\displaystyle{ C_2 }[/math]. And finally, stress points [math]\displaystyle{ (\sigma_\mathrm{n}, \tau_\mathrm{n}) }[/math] satisfying the equation for circle [math]\displaystyle{ C_3 }[/math] lie on, or outside circle [math]\displaystyle{ C_3 }[/math].

See also

• Critical plane analysis

Bibliography

• Beer, Ferdinand Pierre; Elwood Russell Johnston; John T. DeWolf (1992). Mechanics of Materials. McGraw-Hill Professional. ISBN 0-07-112939-1. https://archive.org/details/mechanicsofmater00ferd_1. 
• Brady, B.H.G.; E.T. Brown (1993). Rock Mechanics For Underground Mining (Third ed.). Kluwer Academic Publisher. pp. 17–29. ISBN 0-412-47550-2. https://books.google.com/books?id=s0BaKxL11KsC&pg=PA18. 
• Davis, R. O.; Selvadurai. A. P. S. (1996). Elasticity and geomechanics. Cambridge University Press. pp. 16–26. ISBN 0-521-49827-9. https://books.google.com/books?id=4Z11rZaUn1UC&pg=PA16. 
• Holtz, Robert D.; Kovacs, William D. (1981). An introduction to geotechnical engineering. Prentice-Hall civil engineering and engineering mechanics series. Prentice-Hall. ISBN 0-13-484394-0. https://books.google.com/books?id=yYkYAQAAIAAJ. 
• Jaeger, John Conrad; Cook, N.G.W.; Zimmerman, R.W. (2007). Fundamentals of rock mechanics (Fourth ed.). Wiley-Blackwell. pp. 9–41. ISBN 978-0-632-05759-7. https://books.google.com/books?id=FqADDkunVNAC&pg=PA10. 
• Jumikis, Alfreds R. (1969). Theoretical soil mechanics: with practical applications to soil mechanics and foundation engineering. Van Nostrand Reinhold Co.. ISBN 0-442-04199-3. https://books.google.com/books?id=NPZRAAAAMAAJ. 
• Parry, Richard Hawley Grey (2004). Mohr circles, stress paths and geotechnics (2 ed.). Taylor & Francis. pp. 1–30. ISBN 0-415-27297-1. https://books.google.com/books?id=u_rec9uQnLcC&q=mohr%20circles%2C%20sterss%20paths%20and%20geotechnics&pg=PA1. 
• Timoshenko, Stephen P. (1970). Theory of Elasticity (Third ed.). McGraw-Hill International Editions. ISBN 0-07-085805-5. 
• Timoshenko, Stephen P. (1983). History of strength of materials: with a brief account of the history of theory of elasticity and theory of structures. Dover Books on Physics. Dover Publications. ISBN 0-486-61187-6. 

External links

• Mohr's Circle and more circles by Rebecca Brannon
• DoITPoMS Teaching and Learning Package- "Stress Analysis and Mohr's Circle"