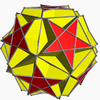
Great icosidodecahedron
| Great icosidodecahedron | |
|---|---|

| |
| Type | Uniform star polyhedron |
| Elements | F = 32, E = 60 V = 30 (χ = 2) |
| Faces by sides | 20{3}+12{5/2} |
| Wythoff symbol | 2 | 3 5/2 2 | 3 5/3 2 | 3/2 5/2 2 | 3/2 5/3 |
| Symmetry group | Ih, [5,3], *532 |
| Index references | U54, C70, W94 |
| Dual polyhedron | Great rhombic triacontahedron |
| Vertex figure |  3.5/2.3.5/2 |
| Bowers acronym | Gid |
File:Great icosidodecahedron.stl In geometry, the great icosidodecahedron is a nonconvex uniform polyhedron, indexed as U54. It has 32 faces (20 triangles and 12 pentagrams), 60 edges, and 30 vertices.[1] It is given a Schläfli symbol r{3,5⁄2}. It is the rectification of the great stellated dodecahedron and the great icosahedron. It was discovered independently by Hess (1878), Badoureau (1881) and Pitsch (1882).
Related polyhedra
The figure is a rectification of the great icosahedron or the great stellated dodecahedron, much as the (small) icosidodecahedron is related to the (small) icosahedron and (small) dodecahedron, and the cuboctahedron to the cube and octahedron.
It shares its vertex arrangement with the icosidodecahedron, which is its convex hull. Unlike the great icosahedron and great dodecahedron, the great icosidodecahedron is not a stellation of the icosidodecahedron, but a faceting of it instead.
It also shares its edge arrangement with the great icosihemidodecahedron (having the triangle faces in common), and with the great dodecahemidodecahedron (having the pentagram faces in common).
 Great icosidodecahedron |
 Great dodecahemidodecahedron |
 Great icosihemidodecahedron |
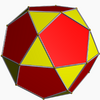 Icosidodecahedron (convex hull) |
The truncated great stellated dodecahedron is a degenerate polyhedron, with 20 triangular faces from the truncated vertices, and 12 (hidden) pentagonal faces as truncations of the original pentagram faces, the latter forming a great dodecahedron inscribed within and sharing the edges of the icosahedron.
| Name | Great stellated dodecahedron |
Truncated great stellated dodecahedron | Great icosidodecahedron |
Truncated great icosahedron |
Great icosahedron |
|---|---|---|---|---|---|
| Coxeter diagram |
|||||
| Picture | 
|

|

|
|

|
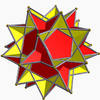
Great rhombic triacontahedron
| Great rhombic triacontahedron | |
|---|---|

| |
| Type | Star polyhedron |
| Face | 
|
| Elements | F = 30, E = 60 V = 32 (χ = 2) |
| Symmetry group | Ih, [5,3], *532 |
| Index references | DU54 |
| dual polyhedron | Great icosidodecahedron |
File:Great rhombic triacontahedron.stl The dual of the great icosidodecahedron is the great rhombic triacontahedron; it is nonconvex, isohedral and isotoxal. It has 30 intersecting rhombic faces. It can also be called the great stellated triacontahedron.
The great rhombic triacontahedron can be constructed by expanding the size of the faces of a rhombic triacontahedron by a factor of τ3 = 1+2τ = 2+√5, where τ is the golden ratio.
See also
Notes
References
- Badoureau (1881), "Mémoire sur les figures isoscèles", Journal de l'École Polytechnique 49: 47–172
- Hess, Edmund (1878), Vier archimedeische Polyeder höherer Art, Cassel. Th. Kay
- Pitsch (1882), "Über halbreguläre Sternpolyeder", Zeitschrift für das Realschulwesen 7
- Wenninger, Magnus (1983), Dual Models, Cambridge University Press, doi:10.1017/CBO9780511569371, ISBN 978-0-521-54325-5
External links
- Weisstein, Eric W.. "Great icosidodecahedron". http://mathworld.wolfram.com/GreatIcosidodecahedron.html.
- Weisstein, Eric W.. "Great rhombic triacontahedron". http://mathworld.wolfram.com/GreatRhombicTriacontahedron.html.
- Uniform polyhedra and duals
 |


