Order-5 dodecahedral honeycomb

Short description: Regular tiling of hyperbolic 3-space

Order-5 dodecahedral honeycomb
Perspective projection view from center of Poincaré disk model
Type	Hyperbolic regular honeycomb Uniform hyperbolic honeycomb
Schläfli symbol	{5,3,5} t0{5,3,5}
Coxeter-Dynkin diagram
Cells	{5,3} (regular dodecahedron)
Faces	{5} (pentagon)
Edge figure	{5} (pentagon)
Vertex figure	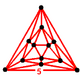icosahedron
Dual	Self-dual
Coxeter group	K3, [5,3,5]
Properties	Regular

In hyperbolic geometry, the order-5 dodecahedral honeycomb is one of four compact regular space-filling tessellations (or honeycombs) in hyperbolic 3-space. With Schläfli symbol {5,3,5}, it has five dodecahedral cells around each edge, and each vertex is surrounded by twenty dodecahedra. Its vertex figure is an icosahedron.

A geometric honeycomb is a space-filling of polyhedral or higher-dimensional cells, so that there are no gaps. It is an example of the more general mathematical tiling or tessellation in any number of dimensions.

Honeycombs are usually constructed in ordinary Euclidean ("flat") space, like the convex uniform honeycombs. They may also be constructed in non-Euclidean spaces, such as hyperbolic uniform honeycombs. Any finite uniform polytope can be projected to its circumsphere to form a uniform honeycomb in spherical space.

Description

The dihedral angle of a Euclidean regular dodecahedron is ~116.6°, so no more than three of them can fit around an edge in Euclidean 3-space. In hyperbolic space, however, the dihedral angle is smaller than it is in Euclidean space, and depends on the size of the figure; the smallest possible dihedral angle is 60°, for an ideal hyperbolic regular dodecahedron with infinitely long edges. The dodecahedra in this dodecahedral honeycomb are sized so that all of their dihedral angles are exactly 72°.

Images

It is analogous to the 2D hyperbolic order-5 pentagonal tiling, {5,5}

Related polytopes and honeycombs

There are four regular compact honeycombs in 3D hyperbolic space:

There is another honeycomb in hyperbolic 3-space called the order-4 dodecahedral honeycomb, {5,3,4}, which has only four dodecahedra per edge. These honeycombs are also related to the 120-cell which can be considered as a honeycomb in positively curved space (the surface of a 4-dimensional sphere), with three dodecahedra on each edge, {5,3,3}. Lastly the dodecahedral ditope, {5,3,2} exists on a 3-sphere, with 2 hemispherical cells.

There are nine uniform honeycombs in the [5,3,5] Coxeter group family, including this regular form. Also the bitruncated form, t_1,2{5,3,5}, , of this honeycomb has all truncated icosahedron cells.

The Seifert–Weber space is a compact manifold that can be formed as a quotient space of the order-5 dodecahedral honeycomb.

This honeycomb is a part of a sequence of polychora and honeycombs with icosahedron vertex figures:

This honeycomb is a part of a sequence of regular polytopes and honeycombs with dodecahedral cells:

Rectified order-5 dodecahedral honeycomb

Rectified order-5 dodecahedral honeycomb
Type	Uniform honeycombs in hyperbolic space
Schläfli symbol	r{5,3,5} t1{5,3,5}
Coxeter diagram
Cells	r{5,3} {3,5}
Faces	triangle {3} pentagon {5}
Vertex figure	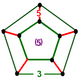pentagonal prism
Coxeter group	[math]\displaystyle{ \overline{K}_3 }[/math], [5,3,5]
Properties	Vertex-transitive, edge-transitive

The rectified order-5 dodecahedral honeycomb, , has alternating icosahedron and icosidodecahedron cells, with a pentagonal prism vertex figure.

Related tilings and honeycomb

It can be seen as analogous to the 2D hyperbolic order-4 pentagonal tiling, r{5,5}

There are four rectified compact regular honeycombs:

Truncated order-5 dodecahedral honeycomb

Truncated order-5 dodecahedral honeycomb
Type	Uniform honeycombs in hyperbolic space
Schläfli symbol	t{5,3,5} t0,1{5,3,5}
Coxeter diagram
Cells	t{5,3} {3,5}
Faces	triangle {3} decagon {10}
Vertex figure	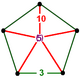pentagonal pyramid
Coxeter group	[math]\displaystyle{ \overline{K}_3 }[/math], [5,3,5]
Properties	Vertex-transitive

The truncated order-5 dodecahedral honeycomb, , has icosahedron and truncated dodecahedron cells, with a pentagonal pyramid vertex figure.

Bitruncated order-5 dodecahedral honeycomb

Bitruncated order-5 dodecahedral honeycomb
Type	Uniform honeycombs in hyperbolic space
Schläfli symbol	2t{5,3,5} t1,2{5,3,5}
Coxeter diagram
Cells	t{3,5}
Faces	pentagon {5} hexagon {6}
Vertex figure	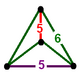tetragonal disphenoid
Coxeter group|[math]\displaystyle{ 2\times\overline{K}_3 }[/math], 5,3,5
Properties	Vertex-transitive, edge-transitive, cell-transitive

The bitruncated order-5 dodecahedral honeycomb, , has truncated icosahedron cells, with a tetragonal disphenoid vertex figure.

Cantellated order-5 dodecahedral honeycomb

Cantellated order-5 dodecahedral honeycomb
Type	Uniform honeycombs in hyperbolic space
Schläfli symbol	rr{5,3,5} t0,2{5,3,5}
Coxeter diagram
Cells	rr{5,3} r{3,5} 40px {}x{5}
Faces	triangle {3} square {4} pentagon {5}
Vertex figure	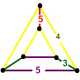wedge
Coxeter group	[math]\displaystyle{ \overline{K}_3 }[/math], [5,3,5]
Properties	Vertex-transitive

The cantellated order-5 dodecahedral honeycomb, , has rhombicosidodecahedron, icosidodecahedron, and pentagonal prism cells, with a wedge vertex figure.

Cantitruncated order-5 dodecahedral honeycomb

Cantitruncated order-5 dodecahedral honeycomb
Type	Uniform honeycombs in hyperbolic space
Schläfli symbol	tr{5,3,5} t0,1,2{5,3,5}
Coxeter diagram
Cells	tr{5,3} t{3,5} 40px {}x{5}
Faces	square {4} pentagon {5} hexagon {6} decagon {10}
Vertex figure	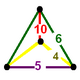mirrored sphenoid
Coxeter group	[math]\displaystyle{ \overline{K}_3 }[/math], [5,3,5]
Properties	Vertex-transitive

The cantitruncated order-5 dodecahedral honeycomb, , has truncated icosidodecahedron, truncated icosahedron, and pentagonal prism cells, with a mirrored sphenoid vertex figure.

Runcinated order-5 dodecahedral honeycomb

Runcinated order-5 dodecahedral honeycomb
Type	Uniform honeycombs in hyperbolic space
Schläfli symbol	t0,3{5,3,5}
Coxeter diagram
Cells	{5,3} {}x{5}
Faces	square {4} pentagon {5}
Vertex figure	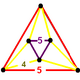triangular antiprism
Coxeter group|[math]\displaystyle{ 2\times\overline{K}_3 }[/math], 5,3,5
Properties	Vertex-transitive, edge-transitive

The runcinated order-5 dodecahedral honeycomb, , has dodecahedron and pentagonal prism cells, with a triangular antiprism vertex figure.

Runcitruncated order-5 dodecahedral honeycomb

Runcitruncated order-5 dodecahedral honeycomb
Type	Uniform honeycombs in hyperbolic space
Schläfli symbol	t0,1,3{5,3,5}
Coxeter diagram
Cells	t{5,3} rr{5,3} 40px {}x{5} 40px {}x{10}
Faces	triangle {3} square {4} pentagon {5} decagon {10}
Vertex figure	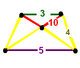isosceles-trapezoidal pyramid
Coxeter group	[math]\displaystyle{ \overline{K}_3 }[/math], [5,3,5]
Properties	Vertex-transitive

The runcitruncated order-5 dodecahedral honeycomb, , has truncated dodecahedron, rhombicosidodecahedron, pentagonal prism, and decagonal prism cells, with an isosceles-trapezoidal pyramid vertex figure.

The runcicantellated order-5 dodecahedral honeycomb is equivalent to the runcitruncated order-5 dodecahedral honeycomb.

Omnitruncated order-5 dodecahedral honeycomb

Omnitruncated order-5 dodecahedral honeycomb
Type	Uniform honeycombs in hyperbolic space
Schläfli symbol	t0,1,2,3{5,3,5}
Coxeter diagram
Cells	tr{5,3} {}x{10}
Faces	square {4} hexagon {6} decagon {10}
Vertex figure	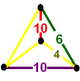phyllic disphenoid
Coxeter group|[math]\displaystyle{ 2\times\overline{K}_3 }[/math], 5,3,5
Properties	Vertex-transitive

The omnitruncated order-5 dodecahedral honeycomb, , has truncated icosidodecahedron and decagonal prism cells, with a phyllic disphenoid vertex figure.

See also

• Convex uniform honeycombs in hyperbolic space
• Regular tessellations of hyperbolic 3-space
• 57-cell - An abstract regular polychoron which shared the {5,3,5} symbol.

References

• Coxeter, Regular Polytopes, 3rd. ed., Dover Publications, 1973. ISBN 0-486-61480-8. (Tables I and II: Regular polytopes and honeycombs, pp. 294–296)
• Coxeter, The Beauty of Geometry: Twelve Essays, Dover Publications, 1999 ISBN 0-486-40919-8 (Chapter 10: Regular honeycombs in hyperbolic space, Summary tables II, III, IV, V, p212-213)
• Norman Johnson Uniform Polytopes, Manuscript
  • N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
  • N.W. Johnson: Geometries and Transformations, (2018) Chapter 13: Hyperbolic Coxeter groups