Astronomy:Galaxy rotation curve

From HandWiki
Revision as of 07:04, 17 February 2024 by Mercury (talk | contribs) (→‎Alternatives to dark matter - LogSE)
(diff) ← Older revision | Latest revision (diff) | Newer revision → (diff)
Short description: Observed discrepancy in galactic angular momenta
Rotation curve of spiral galaxy Messier 33 (yellow and blue points with error bars), and a predicted one from distribution of the visible matter (gray line). The discrepancy between the two curves can be accounted for by adding a dark matter halo surrounding the galaxy.[1][2]

File:Galaxy rotation under the influence of dark matter.ogv The rotation curve of a disc galaxy (also called a velocity curve) is a plot of the orbital speeds of visible stars or gas in that galaxy versus their radial distance from that galaxy's centre. It is typically rendered graphically as a plot, and the data observed from each side of a spiral galaxy are generally asymmetric, so that data from each side are averaged to create the curve. A significant discrepancy exists between the experimental curves observed, and a curve derived by applying gravity theory to the matter observed in a galaxy. Theories involving dark matter are the main postulated solutions to account for the variance.[3]

The rotational/orbital speeds of galaxies/stars do not follow the rules found in other orbital systems such as stars/planets and planets/moons that have most of their mass at the centre. Stars revolve around their galaxy's centre at equal or increasing speed over a large range of distances. In contrast, the orbital velocities of planets in planetary systems and moons orbiting planets decline with distance according to Kepler’s third law. This reflects the mass distributions within those systems. The mass estimations for galaxies based on the light they emit are far too low to explain the velocity observations.[4]

The galaxy rotation problem is the discrepancy between observed galaxy rotation curves and the theoretical prediction, assuming a centrally dominated mass associated with the observed luminous material. When mass profiles of galaxies are calculated from the distribution of stars in spirals and mass-to-light ratios in the stellar disks, they do not match with the masses derived from the observed rotation curves and the law of gravity. A solution to this conundrum is to hypothesize the existence of dark matter and to assume its distribution from the galaxy's center out to its halo.

Though dark matter is by far the most accepted explanation of the rotation problem, other proposals have been offered with varying degrees of success. Of the possible alternatives, one of the most notable is modified Newtonian dynamics (MOND), which involves modifying the laws of gravity.[5]

History

In 1932, Jan Hendrik Oort became the first to report that measurements of the stars in the solar neighborhood indicated that they moved faster than expected when a mass distribution based upon visible matter was assumed, but these measurements were later determined to be essentially erroneous.[6] In 1939, Horace Babcock reported in his PhD thesis measurements of the rotation curve for Andromeda which suggested that the mass-to-luminosity ratio increases radially.[7] He attributed that to either the absorption of light within the galaxy or to modified dynamics in the outer portions of the spiral and not to any form of missing matter. Babcock's measurements turned out to disagree substantially with those found later, and the first measurement of an extended rotation curve in good agreement with modern data was published in 1957 by Henk van de Hulst and collaborators, who studied M31 with the newly commissioned Dwingeloo 25 meter telescope.[8] A companion paper by Maarten Schmidt showed that this rotation curve could be fit by a flattened mass distribution more extensive than the light.[9] In 1959, Louise Volders used the same telescope to demonstrate that the spiral galaxy M33 also does not spin as expected according to Keplerian dynamics.[10]

Reporting on NGC 3115, Jan Oort wrote that "the distribution of mass in the system appears to bear almost no relation to that of light... one finds the ratio of mass to light in the outer parts of NGC 3115 to be about 250".[11] On page 302–303 of his journal article, he wrote that "The strongly condensed luminous system appears imbedded in a large and more or less homogeneous mass of great density" and although he went on to speculate that this mass may be either extremely faint dwarf stars or interstellar gas and dust, he had clearly detected the dark matter halo of this galaxy.

The Carnegie telescope (Carnegie Double Astrograph) was intended to study this problem of Galactic rotation.[12]

In the late 1960s and early 1970s, Vera Rubin, an astronomer at the Department of Terrestrial Magnetism at the Carnegie Institution of Washington, worked with a new sensitive spectrograph that could measure the velocity curve of edge-on spiral galaxies to a greater degree of accuracy than had ever before been achieved.[13] Together with fellow staff-member Kent Ford, Rubin announced at a 1975 meeting of the American Astronomical Society the discovery that most stars in spiral galaxies orbit at roughly the same speed,[14] and that this implied that galaxy masses grow approximately linearly with radius well beyond the location of most of the stars (the galactic bulge). Rubin presented her results in an influential paper in 1980.[15] These results suggested either that Newtonian gravity does not apply universally or that, conservatively, upwards of 50% of the mass of galaxies was contained in the relatively dark galactic halo. Although initially met with skepticism, Rubin's results have been confirmed over the subsequent decades.[16]

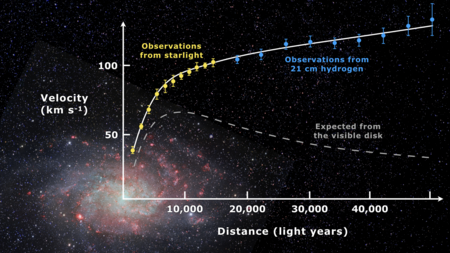
If Newtonian mechanics is assumed to be correct, it would follow that most of the mass of the galaxy had to be in the galactic bulge near the center and that the stars and gas in the disk portion should orbit the center at decreasing velocities with radial distance from the galactic center (the dashed line in Fig. 1).

Observations of the rotation curve of spirals, however, do not bear this out. Rather, the curves do not decrease in the expected inverse square root relationship but are "flat", i.e. outside of the central bulge the speed is nearly a constant (the solid line in Fig. 1). It is also observed that galaxies with a uniform distribution of luminous matter have a rotation curve that rises from the center to the edge, and most low-surface-brightness galaxies (LSB galaxies) have the same anomalous rotation curve.

The rotation curves might be explained by hypothesizing the existence of a substantial amount of matter permeating the galaxy outside of the central bulge that is not emitting light in the mass-to-light ratio of the central bulge. The material responsible for the extra mass was dubbed dark matter, the existence of which was first posited in the 1930s by Jan Oort in his measurements of the Oort constants and Fritz Zwicky in his studies of the masses of galaxy clusters. The existence of non-baryonic cold dark matter (CDM) is today a major feature of the Lambda-CDM model that describes the cosmology of the universe.

Halo density profiles

In order to accommodate a flat rotation curve, a density profile for a galaxy and its environs must be different than one that is centrally concentrated. Newton's version of Kepler's Third Law implies that the spherically symmetric, radial density profile ρ(r) is:

[math]\displaystyle{ \rho(r) = \frac{v(r)^2 }{4 \pi G r^2}\left(1+2~ \frac{d\log v(r)}{d\log r}\right) }[/math]

where v(r) is the radial orbital velocity profile and G is the gravitational constant. This profile closely matches the expectations of a singular isothermal sphere profile where if v(r) is approximately constant then the density ρ ∝ r−2 to some inner "core radius" where the density is then assumed constant. Observations do not comport with such a simple profile, as reported by Navarro, Frenk, and White in a seminal 1996 paper.[17]

The authors then remarked that a "gently changing logarithmic slope" for a density profile function could also accommodate approximately flat rotation curves over large scales. They found the famous Navarro–Frenk–White profile, which is consistent both with N-body simulations and observations given by

[math]\displaystyle{ \rho (r) = \frac{\rho_0}{\frac{r}{R_s}\left(1+\frac{r}{R_s}\right)^2} }[/math]

where the central density, ρ0, and the scale radius, Rs, are parameters that vary from halo to halo.[18] Because the slope of the density profile diverges at the center, other alternative profiles have been proposed, for example the Einasto profile, which has exhibited better agreement with certain dark matter halo simulations.[19][20]

Observations of orbit velocities in spiral galaxies suggest a mass structure according to:

[math]\displaystyle{ v(r) = \left(r \, \frac{d\Phi}{dr}\right)^{1/2} }[/math]

with Φ the galaxy gravitational potential.

Since observations of galaxy rotation do not match the distribution expected from application of Kepler's laws, they do not match the distribution of luminous matter.[15] This implies that spiral galaxies contain large amounts of dark matter or, alternatively, the existence of exotic physics in action on galactic scales. The additional invisible component becomes progressively more conspicuous in each galaxy at outer radii and among galaxies in the less luminous ones.[clarification needed]

A popular interpretation of these observations is that about 26% of the mass of the Universe is composed of dark matter, a hypothetical type of matter which does not emit or interact with electromagnetic radiation. Dark matter is believed to dominate the gravitational potential of galaxies and clusters of galaxies. Under this theory, galaxies are baryonic condensations of stars and gas (namely hydrogen and helium) that lie at the centers of much larger haloes of dark matter, affected by a gravitational instability caused by primordial density fluctuations.

Many cosmologists strive to understand the nature and the history of these ubiquitous dark haloes by investigating the properties of the galaxies they contain (i.e. their luminosities, kinematics, sizes, and morphologies). The measurement of the kinematics (their positions, velocities and accelerations) of the observable stars and gas has become a tool to investigate the nature of dark matter, as to its content and distribution relative to that of the various baryonic components of those galaxies.

Further investigations

Comparison of rotating disc galaxies in the present day (left) and the distant Universe (right).[21]

The rotational dynamics of galaxies are well characterized by their position on the Tully–Fisher relation, which shows that for spiral galaxies the rotational velocity is uniquely related to their total luminosity. A consistent way to predict the rotational velocity of a spiral galaxy is to measure its bolometric luminosity and then read its rotation rate from its location on the Tully–Fisher diagram. Conversely, knowing the rotational velocity of a spiral galaxy gives its luminosity. Thus the magnitude of the galaxy rotation is related to the galaxy's visible mass.[22]

While precise fitting of the bulge, disk, and halo density profiles is a rather complicated process, it is straightforward to model the observables of rotating galaxies through this relationship.[23][better source needed] So, while state-of-the-art cosmological and galaxy formation simulations of dark matter with normal baryonic matter included can be matched to galaxy observations, there is not yet any straightforward explanation as to why the observed scaling relationship exists.[24][25] Additionally, detailed investigations of the rotation curves of low-surface-brightness galaxies (LSB galaxies) in the 1990s[26] and of their position on the Tully–Fisher relation[27] showed that LSB galaxies had to have dark matter haloes that are more extended and less dense than those of galaxies with high surface brightness, and thus surface brightness is related to the halo properties. Such dark-matter-dominated dwarf galaxies may hold the key to solving the dwarf galaxy problem of structure formation.

Very importantly, the analysis of the inner parts of low and high surface brightness galaxies showed that the shape of the rotation curves in the centre of dark-matter dominated systems indicates a profile different from the NFW spatial mass distribution profile.[28][29] This so-called cuspy halo problem is a persistent problem for the standard cold dark matter theory. Simulations involving the feedback of stellar energy into the interstellar medium in order to alter the predicted dark matter distribution in the innermost regions of galaxies are frequently invoked in this context.[30][31]

Alternatives to dark matter

There have been a number of attempts to solve the problem of galaxy rotation by modifying gravity without invoking dark matter. One of the most discussed is modified Newtonian dynamics (MOND), originally proposed by Mordehai Milgrom in 1983, which modifies the Newtonian force law at low accelerations to enhance the effective gravitational attraction. MOND has had a considerable amount of success in predicting the rotation curves of low-surface-brightness galaxies,[32] matching the baryonic Tully–Fisher relation,[33] and the velocity dispersions of the small satellite galaxies of the Local Group.[34]

Using data from the Spitzer Photometry and Accurate Rotation Curves (SPARC) database, a group has found that the radial acceleration traced by rotation curves could be predicted just from the observed baryon distribution (that is, including stars and gas but not dark matter).[35] The same relation provided a good fit for 2693 samples in 153 rotating galaxies, with diverse shapes, masses, sizes, and gas fractions. Brightness in the near infrared, where the more stable light from red giants dominates, was used to estimate the density contribution due to stars more consistently. The results are consistent with MOND, and place limits on alternative explanations involving dark matter alone. However, cosmological simulations within a Lambda-CDM framework that include baryonic feedback effects reproduce the same relation, without the need to invoke new dynamics (such as MOND).[36] Thus, a contribution due to dark matter itself can be fully predictable from that of the baryons, once the feedback effects due to the dissipative collapse of baryons are taken into account. MOND is not a relativistic theory, although relativistic theories which reduce to MOND have been proposed, such as tensor–vector–scalar gravity (TeVeS),[37] scalar–tensor–vector gravity (STVG), and the f(R) theory of Capozziello and De Laurentis,[38] not to mention a version of Superfluid Vacuum theory based on the Logarithmic Schrödinger equation.[39][40][41]

A model of galaxy based on a general relativity metric was also proposed, showing that the rotation curves for the Milky Way, NGC 3031, NGC 3198 and NGC 7331 are consistent with the mass density distributions of the visible matter, avoiding the need for a massive halo of exotic dark matter.[42][43]

According to a 2020 analysis of the data produced by the Gaia spacecraft, it would seem possible to explain at least the Milky Way's rotation curve without requiring any dark matter if instead of a Newtonian approximation the entire set of equations of general relativity is adopted.[44]

In March 2021, Gerson Otto Ludwig published a model based on general relativity that explains galaxy rotation curves with gravitoelectromagnetism.[45]

See also

Footnotes

  1. ↑ Corbelli, E.; Salucci, P. (2000). "The extended rotation curve and the dark matter halo of M33". Monthly Notices of the Royal Astronomical Society 311 (2): 441–447. doi:10.1046/j.1365-8711.2000.03075.x. Bibcode: 2000MNRAS.311..441C. 
  2. ↑ The explanation of the mass discrepancy in spiral galaxies by means of massive and extensive dark component was first put forward by A. Bosma in a PhD dissertation, see
    Bosma, A. (1978). The Distribution and Kinematics of Neutral Hydrogen in Spiral Galaxies of Various Morphological Types (PhD). Rijksuniversiteit Groningen. Retrieved December 30, 2016 – via NASA/IPAC Extragalactic Database.
    See also
    Rubin, V.; Thonnard, N.; Ford, W. K. Jr. (1980). "Rotational Properties of 21 Sc Galaxies With a Large Range of Luminosities and Radii from NGC 4605 (R=4kpc) to UGC 2885 (R=122kpc)". The Astrophysical Journal 238: 471–487. doi:10.1086/158003. Bibcode: 1980ApJ...238..471R. 
    Begeman, K. G.; Broeils, A. H.; Sanders, R.H. (1991). "Extended Rotation Curves of Spiral Galaxies: Dark Haloes and Modified Dynamics". Monthly Notices of the Royal Astronomical Society 249 (3): 523–537. doi:10.1093/mnras/249.3.523. Bibcode: 1991MNRAS.249..523B. 
  3. ↑ Hammond, Richard (May 1, 2008). The Unknown Universe: The Origin of the Universe, Quantum Gravity, Wormholes, and Other Things Science Still Can't Explain. Franklin Lakes, NJ: Career Press. 
  4. ↑ Bosma, A. (1978). The Distribution and Kinematics of Neutral Hydrogen in Spiral Galaxies of Various Morphological Types (PhD). Rijksuniversiteit Groningen. Retrieved December 30, 2016 – via NASA/IPAC Extragalactic Database.
  5. ↑ For an extensive discussion of the data and its fit to MOND see Milgrom, M. (2007). "The MOND Paradigm". arXiv:0801.3133 [astro-ph].
  6. ↑ Oxford Dictionary of Scientists. Oxford: Oxford University Press. 1999. ISBN 978-0-19-280086-2. https://books.google.com/books?id=AtngooiwXikC. 
  7. ↑ Babcock, H. W. (1939). "The rotation of the Andromeda Nebula". Lick Observatory Bulletin 19: 41–51. doi:10.5479/ADS/bib/1939LicOB.19.41B. Bibcode: 1939LicOB..19...41B. 
  8. ↑ Van de Hulst, H.C (1957). "Rotation and density distribution of the Andromeda nebula derived from observations of the 21-cm line". Bulletin of the Astronomical Institutes of the Netherlands 14: 1. Bibcode: 1957BAN....14....1V. 
  9. ↑ Schmidt, M (1957). "Rotation and density distribution of the Andromeda nebula derived from observations of the 21-cm line". Bulletin of the Astronomical Institutes of the Netherlands 14: 17. Bibcode: 1957BAN....14...17S. 
  10. ↑ Volders, L. (1959). "Neutral hydrogen in M 33 and M 101". Bulletin of the Astronomical Institutes of the Netherlands 14 (492): 323. Bibcode: 1959BAN....14..323V. 
  11. ↑ Oort, J.H. (1940), Some Problems Concerning the Structure and Dynamics of the Galactic System and the Elliptical Nebulae NGC 3115 and 4494
  12. ↑ Shane, C. D. (1947). "1947PASP...59..182S Page 182". Publications of the Astronomical Society of the Pacific 59 (349): 182. doi:10.1086/125941. Bibcode: 1947PASP...59..182S. 
  13. ↑ Rubin, V.; Ford, W. K. Jr. (1970). "Rotation of the Andromeda Nebula from a Spectroscopic Survey of Emission Regions". The Astrophysical Journal 159: 379. doi:10.1086/150317. Bibcode: 1970ApJ...159..379R. 
  14. ↑ Rubin, V.C.; Thonnard, N.; Ford, W.K. Jr. (1978). "Extended rotation curves of high-luminosity spiral galaxies. IV – Systematic dynamical properties, SA through SC". The Astrophysical Journal Letters 225: L107–L111. doi:10.1086/182804. Bibcode: 1978ApJ...225L.107R. 
  15. ↑ 15.0 15.1 Rubin, V.; Thonnard, N.; Ford, W. K. Jr. (1980). "Rotational Properties of 21 Sc Galaxies with a Large Range of Luminosities and Radii from NGC 4605 (R=4kpc) to UGC 2885 (R=122kpc)". The Astrophysical Journal 238: 471. doi:10.1086/158003. Bibcode: 1980ApJ...238..471R. 
  16. ↑ Persic, M.; Salucci, P.; Stel, F. (1996). "The universal rotation curve of spiral galaxies – I. The dark matter connection". Monthly Notices of the Royal Astronomical Society 281 (1): 27–47. doi:10.1093/mnras/278.1.27. Bibcode: 1996MNRAS.281...27P. 
  17. ↑ Navarro, J. F.; Frenk, C. S.; White, S. D. M. (1996). "The Structure of Cold Dark Matter Halos". The Astrophysical Journal 463: 563–575. doi:10.1086/177173. Bibcode: 1996ApJ...462..563N. 
  18. ↑ Ostlie, Dale A.; Carroll, Bradley W. (2017). An Introduction to Modern Astrophysics. Cambridge University Press. pp. 918. 
  19. ↑ Merritt, D.; Graham, A.; Moore, B.; Diemand, J.; Terzić, B. (2006). "Empirical Models for Dark Matter Halos. I. Nonparametric Construction of Density Profiles and Comparison with Parametric Models". The Astronomical Journal 132 (6): 2685–2700. doi:10.1086/508988. Bibcode: 2006AJ....132.2685M. 
  20. ↑ Merritt, D.; Navarro, J. F.; Ludlow, A.; Jenkins, A. (2005). "A Universal Density Profile for Dark and Luminous Matter?". The Astrophysical Journal 624 (2): L85–L88. doi:10.1086/430636. Bibcode: 2005ApJ...624L..85M. 
  21. ↑ "Dark Matter Less Influential in Galaxies in Early Universe – VLT observations of distant galaxies suggest they were dominated by normal matter". https://www.eso.org/public/news/eso1709/. 
  22. ↑ Yegorova, I. A.; Salucci, P. (2007). "The radial Tully-Fisher relation for spiral galaxies – I". Monthly Notices of the Royal Astronomical Society 377 (2): 507–515. doi:10.1111/j.1365-2966.2007.11637.x. Bibcode: 2007MNRAS.377..507Y. 
  23. ↑ Dorminey, Bruce (30 Dec 2010). "Reliance on Indirect Evidence Fuels Dark Matter Doubts". Scientific American. http://www.scientificamerican.com/article.cfm?id=dark-matter-doubts&page=2. 
  24. ↑ Weinberg, David H.; et, al. (2008). "Baryon Dynamics, Dark Matter Substructure, and Galaxies". The Astrophysical Journal 678 (1): 6–21. doi:10.1086/524646. Bibcode: 2008ApJ...678....6W. 
  25. ↑ Duffy, Alan R.; al., et (2010). "Impact of baryon physics on dark matter structures: a detailed simulation study of halo density profiles". Monthly Notices of the Royal Astronomical Society 405 (4): 2161–2178. doi:10.1111/j.1365-2966.2010.16613.x. Bibcode: 2010MNRAS.405.2161D. 
  26. ↑ de Blok, W. J. G.; McGaugh, S. (1997). "The dark and visible matter content of low surface brightness disc galaxies". Monthly Notices of the Royal Astronomical Society 290 (3): 533–552. doi:10.1093/mnras/290.3.533. Bibcode: 1997MNRAS.290..533D. 
  27. ↑ Zwaan, M. A.; van der Hulst, J. M.; de Blok, W. J. G.; McGaugh, S. S. (1995). "The Tully-Fisher relation for low surface brightness galaxies: implications for galaxy evolution". Monthly Notices of the Royal Astronomical Society 273 (2): L35–L38. doi:10.1093/mnras/273.1.l35. Bibcode: 1995MNRAS.273L..35Z. 
  28. ↑ Gentile, G.; Salucci, P.; Klein, U.; Vergani, D.; Kalberla, P. (2004). "The cored distribution of dark matter in spiral galaxies". Monthly Notices of the Royal Astronomical Society 351 (3): 903–922. doi:10.1111/j.1365-2966.2004.07836.x. Bibcode: 2004MNRAS.351..903G. 
  29. ↑ de Blok, W. J. G.; Bosma, A. (2002). "High-resolution rotation curves of low surface brightness galaxies". Astronomy & Astrophysics 385 (3): 816–846. doi:10.1051/0004-6361:20020080. Bibcode: 2002A&A...385..816D. https://www.aanda.org/articles/aa/pdf/2002/15/aah3018.pdf. 
  30. ↑ Salucci, P.; De Laurentis, M. (2012). "Dark Matter in galaxies: Leads to its Nature". Proceedings of Science (DSU 2012): 12. Bibcode: 2013arXiv1302.2268S. https://pos.sissa.it/archive/conferences/161/012/DSU%202012_012.pdf. 
  31. ↑ de Blok, W. J. G. (2010). "The Core-Cusp Problem". Advances in Astronomy 2010: 789293. doi:10.1155/2010/789293. Bibcode: 2010AdAst2010E...5D. 
  32. ↑ S. S. McGaugh; W. J. G. de Blok (1998). "Testing the Hypothesis of Modified Dynamics with Low Surface Brightness Galaxies and Other Evidence". Astrophysical Journal 499 (1): 66–81. doi:10.1086/305629. Bibcode: 1998ApJ...499...66M. 
  33. ↑ S. S. McGaugh (2011). "Novel Test of Modified Newtonian Dynamics with Gas Rich Galaxies". Physical Review Letters 106 (12): 121303. doi:10.1103/PhysRevLett.106.121303. PMID 21517295. Bibcode: 2011PhRvL.106l1303M. 
  34. ↑ S. S. McGaugh; M. Milgrom (2013). "Andromeda Dwarfs in Light of Modified Newtonian Dynamics". The Astrophysical Journal 766 (1): 22. doi:10.1088/0004-637X/766/1/22. Bibcode: 2013ApJ...766...22M. 
  35. ↑ Stacy McGaugh; Federico Lelli; Jim Schombert (2016). "The Radial Acceleration Relation in Rotationally Supported Galaxies". Physical Review Letters 117 (20): 201101. doi:10.1103/physrevlett.117.201101. PMID 27886485. Bibcode: 2016PhRvL.117t1101M. 
  36. ↑ Keller, B. W.; Wadsley, J. W. (23 January 2017). "Λ is Consistent with SPARC Radial Acceleration Relation". The Astrophysical Journal 835 (1): L17. doi:10.3847/2041-8213/835/1/L17. Bibcode: 2017ApJ...835L..17K. 
  37. ↑ J. D. Bekenstein (2004). "Relativistic gravitation theory for the modified Newtonian dynamics paradigm". Physical Review D 70 (8): 083509. doi:10.1103/PhysRevD.70.083509. Bibcode: 2004PhRvD..70h3509B. 
  38. ↑ J. W. Moffat (2006). "Scalar tensor vector gravity theory". Journal of Cosmology and Astroparticle Physics 3 (3): 4. doi:10.1088/1475-7516/2006/03/004. Bibcode: 2006JCAP...03..004M. ,S. Capozziello; M. De Laurentis (2012). "The dark matter problem from f(R) gravity viewpoint". Annalen der Physik 524 (9–10): 545–578. doi:10.1002/andp.201200109. Bibcode: 2012AnP...524..545C. 
  39. ↑ Zloshchastiev, Konstantin G. (2020). "An Alternative to Dark Matter and Dark Energy: Scale-Dependent Gravity in Superfluid Vacuum Theory". Universe 6 (180): 180. doi:10.3390/universe6100180. ISSN 2218-1997. Bibcode: 2020Univ....6..180Z. 
  40. ↑ Zloshchastiev, Konstantin G. (2023). "Galaxy rotation curves in superfluid vacuum theory". Pramana - Journal of Physics 97 (2): 2. doi:10.1007/s12043-022-02480-2. Bibcode: 2023Prama..97....2Z. 
  41. ↑ Scott, T.C. (2023). "From Modified Newtonian Dynamics to Superfluid Vacuum Theory". Entropy 25 (12): 12. doi:10.3390/e25010012. PMID 36673152. 
  42. ↑ Cooperstock, Fred I., and S. Tieu. "General relativity resolves galactic rotation without exotic dark matter." arXiv preprint astro-ph/0507619 (2005).
  43. ↑ Cooperstock, F. I.; Tieu, S. (2007-05-20). "Galactic Dynamics Via General Relativity: A Compilation and New Developments" (in en). International Journal of Modern Physics A 22 (13): 2293–2325. doi:10.1142/S0217751X0703666X. ISSN 0217-751X. Bibcode: 2007IJMPA..22.2293C. https://www.worldscientific.com/doi/abs/10.1142/S0217751X0703666X. 
  44. ↑ Crosta, Mariateresa; Giammaria, Marco; Lattanzi, Mario G.; Poggio, Eloisa (August 2020). "On testing CDM and geometry-driven Milky Way rotation curve models with Gaia DR2". Monthly Notices of the Royal Astronomical Society (OUP) 496 (2): 2107–2122. doi:10.1093/mnras/staa1511. 
  45. ↑ Ludwig, G. O. (2021-02-23). "Galactic rotation curve and dark matter according to gravitomagnetism". The European Physical Journal C 81 (2): 186. doi:10.1140/epjc/s10052-021-08967-3. Bibcode: 2021EPJC...81..186L. 

Further reading

Bibliography

  • Galactic Astronomy, Dmitri Mihalas and Paul McRae.W. H. Freeman 1968.

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Astronomy:Galaxy_rotation_curve&oldid=3693555"