Astronomy:Void

| Part of a series on |
| Physical cosmology |
|---|
 |
Cosmic voids (also known as dark space) are vast spaces between filaments (the largest-scale structures in the universe), which contain very few or no galaxies. Most galaxies are not located in voids, despite their size, due to most galaxies being gravitationally bound together, creating huge cosmic structures known as galaxy filaments. The cosmological evolution of the void regions differs drastically from the evolution of the Universe as a whole: there is a long stage when the curvature term dominates, which prevents the formation of galaxy clusters and massive galaxies. Hence, although even the emptiest regions of voids contain more than ~15% of the average matter density of the Universe, the voids look almost empty to an observer.[1]
Voids typically have a diameter of 10 to 100 megaparsecs (30 to 300 million light-years); particularly large voids, defined by the absence of rich superclusters, are sometimes called supervoids. They were first discovered in 1978 in a pioneering study by Stephen Gregory and Laird A. Thompson at the Kitt Peak National Observatory.[2]
Voids are believed to have been formed by baryon acoustic oscillations in the Big Bang, collapses of mass followed by implosions of the compressed baryonic matter. Starting from initially small anisotropies from quantum fluctuations in the early universe, the anisotropies grew larger in scale over time. Regions of higher density collapsed more rapidly under gravity, eventually resulting in the large-scale, foam-like structure or "cosmic web" of voids and galaxy filaments seen today. Voids located in high-density environments are smaller than voids situated in low-density spaces of the universe.[3]
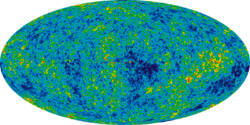
Voids appear to correlate with the observed temperature of the cosmic microwave background (CMB) because of the Sachs–Wolfe effect. Colder regions correlate with voids, and hotter regions correlate with filaments because of gravitational redshifting. As the Sachs–Wolfe effect is only significant if the universe is dominated by radiation or dark energy, the existence of voids is significant in providing physical evidence for dark energy.[4][5]
Large-scale structure
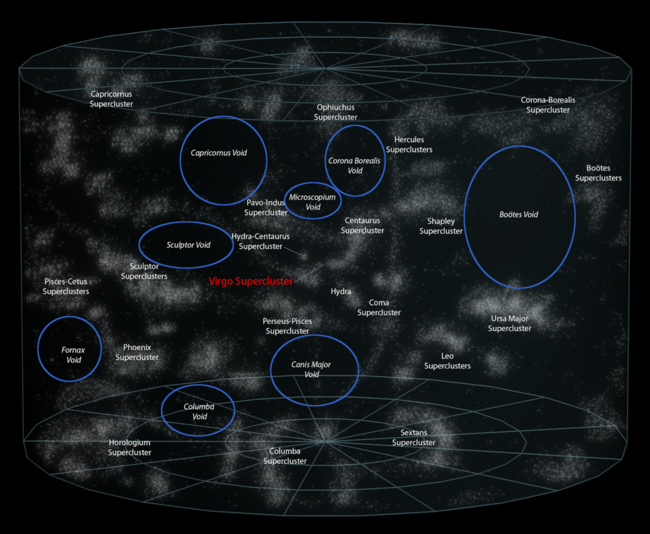
The structure of the Universe can be broken down into components that can help describe the characteristics of individual regions of the cosmos. These are the main structural components of the cosmic web:
- Voids – vast, largely spherical[6] regions with very low cosmic mean densities, up to 100 megaparsecs (Mpc) in diameter.[7]
- Walls – the regions that contain the typical cosmic mean density of matter abundance. Walls can be further broken down into two smaller structural features:
Voids have a mean density less than a tenth of the average density of the universe. This serves as a working definition even though there is no single agreed-upon definition of what constitutes a void. The matter density value used for describing the cosmic mean density is usually based on a ratio of the number of galaxies per unit volume rather than the total mass of the matter contained in a unit volume.[9]
Discovery
Study of cosmic voids within the discipline of astrophysics began in the mid-1970s when redshift surveys led two separate teams of astrophysicists in 1978 to identify superclusters and voids in the distribution of galaxies and Abell clusters.[10][11] The new redshift surveys revolutionized the field of astronomy by adding depth to the two-dimensional maps of cosmological structure, which were often densely packed and overlapping,[7] allowing for the first three-dimensional mapping of the universe. Through redshift surveys, their depth was calculated from the individual redshifts of the galaxies due to the expansion of the universe according to Hubble's law.[12]
Timeline
A summarized timeline of important events in the field of cosmic voids from its beginning to recent times is as follows:
- 1961 – Large-scale structural features such as "second-order clusters", a specific type of supercluster, were brought to the astronomical community's attention.[13]
- 1978 – The first two papers on the topic of voids in the large-scale structure were published referencing voids found in the foreground of the Coma/A1367 clusters.[10][14]
- 1981 – Discovery of a large void in the Boötes region of the sky that was nearly 50 h−1 Mpc in diameter (which was later recalculated to be about 34 h−1 Mpc).[15][16] Here h is the dimensionless Hubble parameter, approximately 0.7.
- 1983 – Computer simulations sophisticated enough to provide relatively reliable results of growth and evolution of the large-scale structure emerged and yielded insight on key features of the large-scale galaxy distribution.[17][18]
- 1985 – Details of the supercluster and void structure of the Perseus–Pisces region were surveyed.[19]
- 1989 – The Center for Astrophysics Redshift Survey revealed that large voids, sharp filaments, and the walls that surround them dominate the large-scale structure of the universe.[20]
- 1991 – The Las Campanas Redshift Survey confirmed the abundance of voids in the large-scale structure of the universe (Kirshner et al. 1991).[21]
- 1995 – Comparisons of optically selected galaxy surveys indicate that the same voids are found regardless of the sample selection.[22]
- 2001 – The completed two-degree Field Galaxy Redshift Survey adds a significantly large amount of voids to the database of all known cosmic voids.[23]
- 2009 – The Sloan Digital Sky Survey (SDSS) data combined with previous large-scale surveys now provide the most complete view of the detailed structure of cosmic voids.[24][25][26]
Methods for finding
There exist a number of ways for finding voids with the results of large-scale surveys of the universe. Of the many different algorithms, virtually all fall into one of three general categories.[27] The first class consists of void finders that try to find empty regions of space based on local galaxy density.[28] The second class are those which try to find voids via the geometrical structures in the dark matter distribution as suggested by the galaxies.[29] The third class is made up of those finders which identify structures dynamically by using gravitationally unstable points in the distribution of dark matter.[30] The three most popular methods through the study of cosmic voids are listed below:
VoidFinder algorithm
This first-class method uses each galaxy in a catalog as its target and then uses the Nearest Neighbor Approximation to calculate the cosmic density in the region contained in a spherical radius determined by the distance to the third-closest galaxy.[31] El Ad & Piran introduced this method in 1997 to allow a quick and effective method for standardizing the cataloging of voids. Once the spherical cells are mined from all of the structure data, each cell is expanded until the underdensity returns to average expected wall density values.[32] One of the helpful features of void regions is that their boundaries are very distinct and defined, with a cosmic mean density that starts at 10% in the body and quickly rises to 20% at the edge and then to 100% in the walls directly outside the edges. The remaining walls and overlapping void regions are then gridded into, respectively, distinct and intertwining zones of filaments, clusters, and near-empty voids. Any overlap of more than 10% with already known voids are considered to be subregions within those known voids. All voids admitted to the catalog had a minimum radius of 10 Mpc in order to ensure all identified voids were not accidentally cataloged due to sampling errors.[31]
Zone bordering on voidness (ZOBOV) algorithm
This particular second-class algorithm uses a Voronoi tessellation technique and mock border particles in order to categorize regions based on a high-density contrasting border with a very low amount of bias.[33] Neyrinck introduced this algorithm in 2008 with the purpose of introducing a method that did not contain free parameters or presumed shape tessellations. Therefore, this technique can create more accurately shaped and sized void regions. Although this algorithm has some advantages in shape and size, it has been criticized often for sometimes providing loosely defined results. Since it has no free parameters, it mostly finds small and trivial voids, although the algorithm places a statistical significance on each void it finds. A physical significance parameter can be applied in order to reduce the number of trivial voids by including a minimum density to average density ratio of at least 1:5. Subvoids are also identified using this process which raises more philosophical questions on what qualifies as a void.[34] Void finders such as VIDE[35] are based on ZOBOV.
Dynamical void analysis (DIVA) algorithm
This third-class method is drastically different from the previous two algorithms listed. The most striking aspect is that it requires a different definition of what it means to be a void. Instead of the general notion that a void is a region of space with a low cosmic mean density; a hole in the distribution of galaxies, it defines voids to be regions in which matter is escaping; which corresponds to the dark energy equation of state, w. Void centers are then considered to be the maximal source of the displacement field denoted as Sψ. The purpose for this change in definitions was presented by Lavaux and Wandelt in 2009 as a way to yield cosmic voids such that exact analytical calculations can be made on their dynamical and geometrical properties. This allows DIVA to heavily explore the ellipticity of voids and how they evolve in the large-scale structure, subsequently leading to the classification of three distinct types of voids. These three morphological classes are True voids, Pancake voids, and Filament voids. Another notable quality is that even though DIVA also contains selection function bias just as first-class methods do, DIVA is devised such that this bias can be precisely calibrated, leading to much more reliable results. Multiple shortfalls of this Lagrangian-Eulerian hybrid approach exist. One example is that the resulting voids from this method are intrinsically different than those found by other methods, which makes an all-data points inclusive comparison between results of differing algorithms very difficult.[27]
Significance
Voids have contributed significantly to the modern understanding of the cosmos, with applications ranging from shedding light on the current understanding of dark energy, to refining and constraining cosmological evolution models. The Milky Way Galaxy is in a cosmic void named the KBC Void.[36] Some popular applications are mentioned in detail below.
Dark energy
The simultaneous existence of the largest-known voids and galaxy clusters requires about 70% dark energy in the universe today, consistent with the latest data from the cosmic microwave background.[5] Voids act as bubbles in the universe that are sensitive to background cosmological changes. This means that the evolution of a void's shape is in part the result of the expansion of the universe. Since this acceleration is believed to be caused by dark energy, studying the changes of a void's shape over a period of time can be used to constrain the standard ΛCDM model,[37][38] or further refine the Quintessence + Cold Dark Matter (QCDM) model and provide a more accurate dark energy equation of state.[39] Additionally the abundance of voids is a promising way to constrain the dark energy equation of state.[40][41]
Neutrinos
Neutrinos, due to their very small mass and extremely weak interaction with other matter, will free-stream in and out of voids which are smaller than the mean-free path of neutrinos. This has an effect on the size and depth distribution of voids, and is expected to make it possible with future astronomical surveys (e.g. the Euclid satellite) to measure the sum of the masses of all neutrino species by comparing the statistical properties of void samples to theoretical predictions.[41]
Galactic formation and evolution models
Cosmic voids contain a mix of galaxies and matter that is slightly different than other regions in the universe. This unique mix supports the biased galaxy formation picture predicted in Gaussian adiabatic cold dark matter models. This phenomenon provides an opportunity to modify the morphology-density correlation that holds discrepancies with these voids. Such observations like the morphology-density correlation can help uncover new facets about how galaxies form and evolve on the large scale.[42] On a more local scale, galaxies that reside in voids have differing morphological and spectral properties than those that are located in the walls. One feature that has been found is that voids have been shown to contain a significantly higher fraction of starburst galaxies of young, hot stars when compared to samples of galaxies in walls.[43]
Voids offer opportunities to study the strength of intergalactic magnetic fields. For example, a 2015 study concluded, based on the deflection of blazar gamma-ray emissions that travel through voids, that intergalactic space contains a magnetic field of strength at least 10-17 G. The specific large-scale magnetic structure of the universe suggests primordial "magnetogenesis", which in turn could have played a role in the formation of magnetic fields within galaxies, and could also change estimates of the timeline of recombination in the early universe.[44][45]
Anomalies in anisotropies
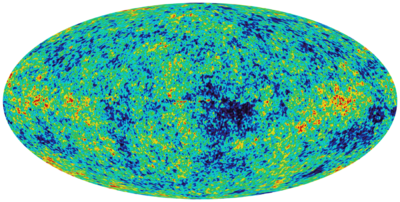
Cold spots in the cosmic microwave background, such as the WMAP cold spot found by Wilkinson Microwave Anisotropy Probe, could possibly be explained by an extremely large cosmic void that has a radius of ~120 Mpc, as long as the late integrated Sachs–Wolfe effect was accounted for in the possible solution. Anomalies in CMB screenings are now being potentially explained through the existence of large voids located down the line-of-sight in which the cold spots lie.[46]
Expansion
Although dark energy is currently the most popular explanation for the acceleration in the expansion of the universe, another theory elaborates on the possibility of our galaxy being part of a very large, not-so-underdense, cosmic void. According to this theory, such an environment could naively lead to the demand for dark energy to solve the problem with the observed acceleration. As more data has been released on this topic the chances of it being a realistic solution in place of the current ΛCDM interpretation has been largely diminished but not all together abandoned.[47]
Gravitational theories
The abundance of voids, particularly when combined with the abundance of clusters of galaxies, is a promising method for precision tests of deviations from general relativity on large scales and in low-density regions.[48][49]
The insides of voids often seem to adhere to cosmological parameters which differ from those of the known universe[citation needed]. It is because of this unique feature that cosmic voids are useful laboratories to study the effects that gravitational clustering and growth rates have on local galaxies and structure when the cosmological parameters have different values from the outside universe. Due to the observation that larger voids predominantly remain in a linear regime, with most structures within exhibiting spherical symmetry in the underdense environment; that is, the underdensity leads to near-negligible particle-particle gravitational interactions that would otherwise occur in a region of normal galactic density. Testing models for voids can be performed with very high accuracy. The cosmological parameters that differ in these voids are Ωm, ΩΛ, and H0.[50]
See also
References
- ↑ Baushev, A. N. (2021). "The central region of a void: an analytical solution". Monthly Notices of the Royal Astronomical Society: Letters 504 (1): L56–L60. doi:10.1093/mnrasl/slab036. Bibcode: 2021MNRAS.504L..56B.
- ↑ Freedman, R. A., & Kaufmann III, W. J. (2008). Stars and galaxies: Universe. New York City: W.H. Freeman and Company.
- ↑ U. Lindner; J. Einasto; M. Einasto; W. Freudling; K. Fricke; E. Tago (1995). "The structure of supervoids. I. Void hierarchy in the Northern Local Supervoid". Astron. Astrophys. 301: 329. Bibcode: 1995A&A...301..329L.
- ↑ Granett, B. R.; Neyrinck, M. C.; Szapudi, I. (2008). "An Imprint of Superstructures on the Microwave Background due to the Integrated Sachs-Wolfe Effect". Astrophysical Journal 683 (2): L99–L102. doi:10.1086/591670. Bibcode: 2008ApJ...683L..99G.
- ↑ 5.0 5.1 Sahlén, Martin; Zubeldía, Íñigo; Silk, Joseph (2016). "Cluster–Void Degeneracy Breaking: Dark Energy, Planck, and the Largest Cluster and Void" (in en). The Astrophysical Journal Letters 820 (1): L7. doi:10.3847/2041-8205/820/1/L7. ISSN 2041-8205. Bibcode: 2016ApJ...820L...7S. http://stacks.iop.org/2041-8205/820/i=1/a=L7.
- ↑ Ryden, Barbara Sue; Peterson, Bradley M. (2010-01-01) (in en). Foundations of Astrophysics (International ed.). Addison-Wesley. p. 522. ISBN 9780321595584. https://books.google.com/books?id=1p7tOwAACAAJ.
- ↑ 7.0 7.1 Carroll, Bradley W.; Ostlie, Dale A. (2013-07-23) (in en). An Introduction to Modern Astrophysics (International ed.). Pearson. p. 1171. ISBN 9781292022932. https://books.google.com/books?id=RLwangEACAAJ.
- ↑ Pan, Danny C.; Michael S. Vogeley; Fiona Hoyle; Yun-Young Choi; Changbom Park (23 Mar 2011). "Cosmic Voids in Sloan Digital Sky Survey Data Release 7". Monthly Notices of the Royal Astronomical Society 421 (2): 926–934. doi:10.1111/j.1365-2966.2011.20197.x. Bibcode: 2012MNRAS.421..926P.
- ↑ Neyrinck, Mark C. (29 Feb 2008). "ZOBOV: a parameter-free void-finding algorithm". Monthly Notices of the Royal Astronomical Society 386 (4): 2101–2109. doi:10.1111/j.1365-2966.2008.13180.x. Bibcode: 2008MNRAS.386.2101N.
- ↑ 10.0 10.1 Gregory, S. A.; Thompson, L. A. (1978). "The Coma/A1367 supercluster and its environs". The Astrophysical Journal 222: 784. doi:10.1086/156198. ISSN 0004-637X. Bibcode: 1978ApJ...222..784G. http://digitalcommons.unl.edu/cgi/viewcontent.cgi?article=1092&context=physicsfacpub.
- ↑ Jõeveer, M.; Einasto, J. (1978). Longair, M. S.. ed (in en). The Large Scale Structure of the Universe. Dordrecht: Reidel. p. 241.
- ↑ Rex, Andrew F.; Bennett, Jeffrey O.; Donahue, Megan; Schneider, Nicholas; Voit, Mark (1998-12-01). The Cosmic Perspective. Pearson College Division. p. 602. ISBN 978-0-201-47399-5. https://books.google.com/books?id=L9R9AAAACAAJ. Retrieved 4 May 2014.
- ↑ Abell, George O. (1961). "Evidence regarding second-order clustering of galaxies and interactions between clusters of galaxies". The Astronomical Journal 66: 607. doi:10.1086/108472. ISSN 0004-6256. Bibcode: 1961AJ.....66..607A.
- ↑ Joeveer, Einasto and Tago 1978, Dordrecht, N/A, 241.
- ↑ Kirshner, R. P.; Oemler, A. Jr.; Schechter, P. L.; Shectman, S. A. (1981). "A million cubic megaparsec void in Bootes". The Astrophysical Journal 248: L57. doi:10.1086/183623. ISSN 0004-637X. Bibcode: 1981ApJ...248L..57K.
- ↑ Kirshner, Robert P.; Oemler, Augustus Jr.; Schechter, Paul L.; Shectman, Stephen A. (1987). "A survey of the Bootes void". The Astrophysical Journal 314: 493. doi:10.1086/165080. ISSN 0004-637X. Bibcode: 1987ApJ...314..493K.
- ↑ Merlott, A. L. (November 1983). "Clustering velocities in the adiabatic picture of galaxy formation". Monthly Notices of the Royal Astronomical Society 205 (3): 637–641. doi:10.1093/mnras/205.3.637. ISSN 0035-8711. Bibcode: 1983MNRAS.205..637M.
- ↑ Frenk, C. S.; White, S. D. M.; Davis, M. (1983). "Nonlinear evolution of large-scale structure in the universe". The Astrophysical Journal 271: 417. doi:10.1086/161209. ISSN 0004-637X. Bibcode: 1983ApJ...271..417F.
- ↑ Giovanelli, R.; Haynes, M. P. (1985). "A 21 CM survey of the Pisces-Perseus supercluster. I – The declination zone +27.5 to +33.5 degrees". The Astronomical Journal 90: 2445. doi:10.1086/113949. ISSN 0004-6256. Bibcode: 1985AJ.....90.2445G.
- ↑ Geller, M. J.; Huchra, J. P. (1989). "Mapping the Universe". Science 246 (4932): 897–903. doi:10.1126/science.246.4932.897. ISSN 0036-8075. PMID 17812575. Bibcode: 1989Sci...246..897G.
- ↑ Kirshner, 1991, Physical Cosmology, 2, 595.
- ↑ Fisher, Karl; Huchra, John; Strauss, Michael; Davis, Marc; Yahil, Amos; Schlegel, David (1995). "The IRAS 1.2 Jy Survey: Redshift Data". The Astrophysical Journal Supplement Series 100: 69. doi:10.1086/192208. Bibcode: 1995ApJS..100...69F.
- ↑ Colless, Matthew; Dalton, G. B.; Maddox, S. J.; Sutherland, W. J.; Norberg, P.; Cole, S.; Bland-Hawthorn, J.; Bridges, T. J. et al. (2001). "The 2dF Galaxy Redshift Survey: Spectra and redshifts". Monthly Notices of the Royal Astronomical Society 328 (4): 1039–1063. doi:10.1046/j.1365-8711.2001.04902.x. Bibcode: 2001MNRAS.328.1039C.
- ↑ Abazajian, K.; for the Sloan Digital Sky Survey; Agüeros, Marcel A.; Allam, Sahar S.; Prieto, Carlos Allende; An, Deokkeun; Anderson, Kurt S. J.; Anderson, Scott F. et al. (2009). "The Seventh Data Release of the Sloan Digital Sky Survey". The Astrophysical Journal Supplement Series 182 (2): 543–558. doi:10.1088/0067-0049/182/2/543. Bibcode: 2009ApJS..182..543A.
- ↑ Thompson, Laird A.; Gregory, Stephen A. (2011). "An Historical View: The Discovery of Voids in the Galaxy Distribution". arXiv:1109.1268 [physics.hist-ph].
- ↑ Mao, Qingqing; Berlind, Andreas A.; Scherrer, Robert J.; Neyrinck, Mark C.; Scoccimarro, Román; Tinker, Jeremy L.; McBride, Cameron K.; Schneider, Donald P. et al. (2017). "A Cosmic Void Catalog of SDSS DR12 BOSS Galaxies" (in en). The Astrophysical Journal 835 (2): 161. doi:10.3847/1538-4357/835/2/161. ISSN 0004-637X. Bibcode: 2017ApJ...835..161M. http://stacks.iop.org/0004-637X/835/i=2/a=161.
- ↑ 27.0 27.1 Lavaux, Guilhem; Wandelt, Benjamin D. (2010). "Precision cosmology with voids: Definition, methods, dynamics". Monthly Notices of the Royal Astronomical Society 403 (3): 403–1408. doi:10.1111/j.1365-2966.2010.16197.x. Bibcode: 2010MNRAS.403.1392L.
- ↑ Hoyle, Fiona; Vogeley, Michael S. (2002). "Voids in the PSCz Survey and the Updated Zwicky Catalog". The Astrophysical Journal 566 (2): 641–651. doi:10.1086/338340. Bibcode: 2002ApJ...566..641H.
- ↑ Colberg, Joerg M.; Sheth, Ravi K.; Diaferio, Antonaldo; Gao, Liang; Yoshida, Naoki (2005). "Voids in a [Lambda] CDM Universe". Monthly Notices of the Royal Astronomical Society 360 (1): 216–226. doi:10.1111/j.1365-2966.2005.09064.x. Bibcode: 2005MNRAS.360..216C.
- ↑ Hahn, Oliver; Porciani, Cristiano; Marcella Carollo, C.; Dekel, Avishai (2007). "Properties of Dark Matter Haloes in Clusters, Filaments, Sheets and Voids". Monthly Notices of the Royal Astronomical Society 375 (2): 489–499. doi:10.1111/j.1365-2966.2006.11318.x. Bibcode: 2007MNRAS.375..489H.
- ↑ 31.0 31.1 Pan, Danny C.; Vogeley, Michael S.; Hoyle, Fiona; Choi, Yun-Young; Park, Changbom (2011). "Cosmic Voids in Sloan Digital Sky Survey Data Release 7". Monthly Notices of the Royal Astronomical Society 421 (2): 926–934. doi:10.1111/j.1365-2966.2011.20197.x. Bibcode: 2012MNRAS.421..926P.
- ↑ El-Ad, Hagai; Piran, Tsvi (1997). "Voids in the Large-Scale Structure". The Astrophysical Journal 491 (2): 421–435. doi:10.1086/304973. Bibcode: 1997ApJ...491..421E.
- ↑ Sutter, P. M.; Lavaux, Guilhem; Wandelt, Benjamin D.; Weinberg, David H. (2013). "A response to arXiv:1310.2791: A self-consistent public catalogue of voids and superclusters in the SDSS Data Release 7 galaxy surveys". arXiv:1310.5067 [astro-ph.CO].
- ↑ Neyrinck, Mark C. (2008). "ZOBOV: A parameter-free void-finding algorithm". Monthly Notices of the Royal Astronomical Society 386 (4): 2101–2109. doi:10.1111/j.1365-2966.2008.13180.x. Bibcode: 2008MNRAS.386.2101N.
- ↑ Sutter, P. M. (2015). "VIDE: The Void IDentification and Examination toolkit". Astronomy and Computing 9: 1–9. doi:10.1016/j.ascom.2014.10.002. Bibcode: 2015A&C.....9....1S.
- ↑ Howell, Elizabeth (2017-06-14). "We Live in a Cosmic Void, Another Study Confirms" (in en-us). https://www.space.com/37191-we-live-in-a-cosmic-void.html.
- ↑ Lavaux, Guilhem; Wandelt, Benjamin D. (1 August 2012). "Precision Cosmography with Stacked Voids". The Astrophysical Journal 754 (2): 109. doi:10.1088/0004-637X/754/2/109. Bibcode: 2012ApJ...754..109L.
- ↑ Mao, Qingqing; Berlind, Andreas A.; Scherrer, Robert J.; Neyrinck, Mark C.; Scoccimarro, Román; Tinker, Jeremy L.; McBride, Cameron K.; Schneider, Donald P. (25 January 2017). "Cosmic Voids in the SDSS DR12 BOSS Galaxy Sample: the Alcock–Paczyński test". The Astrophysical Journal 835 (2): 160. doi:10.3847/1538-4357/835/2/160. Bibcode: 2017ApJ...835..160M.
- ↑ Lee, Jounghun; Park, Daeseong (2007). "Constraining the Dark Energy Equation of State with Cosmic Voids". The Astrophysical Journal 696 (1): L10–L12. doi:10.1088/0004-637X/696/1/L10. Bibcode: 2009ApJ...696L..10L.
- ↑ Pisani, Alice; Sutter, P. M.; Hamaus, Nico; Alizadeh, Esfandiar; Biswas, Rahul; Wandelt, Benjamin D.; Hirata, Christopher M. (2015). "Counting voids to probe dark energy". Physical Review D 92 (8): 083531. doi:10.1103/PhysRevD.92.083531. Bibcode: 2015PhRvD..92h3531P.
- ↑ 41.0 41.1 Sahlén, Martin (2019-03-22). "Cluster-void degeneracy breaking: Neutrino properties and dark energy" (in en). Physical Review D 99 (6): 063525. doi:10.1103/PhysRevD.99.063525. ISSN 2470-0010. Bibcode: 2019PhRvD..99f3525S.
- ↑ Peebles, P. J. E. (2001). "The Void Phenomenon". The Astrophysical Journal 557 (2): 495–504. doi:10.1086/322254. Bibcode: 2001ApJ...557..495P.
- ↑ Constantin, Anca; Hoyle, Fiona; Vogeley, Michael S. (2007). "Active Galactic Nuclei in Void Regions". The Astrophysical Journal 673 (2): 715–729. doi:10.1086/524310. Bibcode: 2008ApJ...673..715C.
- ↑ Wolchover, Natalie (2 July 2020). "The Hidden Magnetic Universe Begins to Come Into View" (in en). Quanta Magazine. https://www.quantamagazine.org/the-hidden-magnetic-universe-begins-to-come-into-view-20200702/.
- ↑ Chen, Wenlei; Buckley, James H.; Ferrer, Francesc (16 November 2015). "Search for GeV γ-Ray Pair Halos Around Low Redshift Blazars". Physical Review Letters 115 (21): 211103. doi:10.1103/PhysRevLett.115.211103. PMID 26636838. Bibcode: 2015PhRvL.115u1103C.
- ↑ Rudnick, Lawrence; Brown, Shea; Williams, Liliya R. (2007). "Extragalactic Radio Sources and the WMAP Cold Spot". The Astrophysical Journal 671 (1): 40–44. doi:10.1086/522222. Bibcode: 2007ApJ...671...40R.
- ↑ Alexander, Stephon; Biswas, Tirthabir; Notari, Alessio; Vaid, Deepak (2009). "Local Void vs Dark Energy: Confrontation with WMAP and Type Ia Supernovae". Journal of Cosmology and Astroparticle Physics 2009 (9): 025. doi:10.1088/1475-7516/2009/09/025. Bibcode: 2009JCAP...09..025A.
- ↑ Sahlén, Martin; Silk, Joseph (2018-05-03). "Cluster-void degeneracy breaking: Modified gravity in the balance". Physical Review D 97 (10): 103504. doi:10.1103/PhysRevD.97.103504. Bibcode: 2018PhRvD..97j3504S.
- ↑ Nan, Yue; Yamamoto, Kazuhiro (2018-08-28). "Gravitational redshift in the void-galaxy cross-correlation function in redshift space". Physical Review D 98 (4): 043527. doi:10.1103/PhysRevD.98.043527. Bibcode: 2018PhRvD..98d3527N.
- ↑ Goldberg, David M.; Vogeley, Michael S. (2004). "Simulating Voids". The Astrophysical Journal 605 (1): 1–6. doi:10.1086/382143. Bibcode: 2004ApJ...605....1G.
Further reading
- Lemonick, Michael D., "Cosmic Nothing: Huge empty patches of the universe could help solve some of the greatest mysteries in the cosmos", Scientific American, vol. 330, no. 1 (January 2024), pp. 20–27.
External links
- Animated views of voids and their distribution from Hume Feldman with Sergei Shandarin, Dept. Physics and Astronomy, University of Kansas, Lawrence, Kansas, USA.
- Visualization of Nearby Large-Scale Structures Fairall, A. P.; Paverd, W. R.; & Ashley, R. P.
