6-simplex

In geometry, a 6-simplex is a self-dual regular 6-polytope. It has 7 vertices, 21 edges, 35 triangle faces, 35 tetrahedral cells, 21 5-cell 4-faces, and 7 5-simplex 5-faces. Its dihedral angle is cos⁻¹(1/6), or approximately 80.41°.

Alternate names

It can also be called a heptapeton, or hepta-6-tope, as a 7-facetted polytope in 6-dimensions. The name heptapeton is derived from hepta for seven facets in Greek and -peta for having five-dimensional facets, and -on. Jonathan Bowers gives a heptapeton the acronym hop.

As a configuration

This configuration matrix represents the 6-simplex. The rows and columns correspond to vertices, edges, faces, cells, 4-faces and 5-faces. The diagonal numbers say how many of each element occur in the whole 6-simplex. The nondiagonal numbers say how many of the column's element occur in or at the row's element. This self-dual simplex's matrix is identical to its 180 degree rotation.

[math]\displaystyle{ \begin{bmatrix}\begin{matrix}7 & 6 & 15 & 20 & 15 & 6 \\ 2 & 21 & 5 & 10 & 10 & 5 \\ 3 & 3 & 35 & 4 & 6 & 4 \\ 4 & 6 & 4 & 35 & 3 & 3 \\ 5 & 10 & 10 & 5 & 21 & 2 \\ 6 & 15 & 20 & 15 & 6 & 7 \end{matrix}\end{bmatrix} }[/math]

The Cartesian coordinates for an origin-centered regular heptapeton having edge length 2 are:

[math]\displaystyle{ \left(\sqrt{1/21},\ \sqrt{1/15},\ \sqrt{1/10},\ \sqrt{1/6},\ \sqrt{1/3},\ \pm1\right) }[/math]

[math]\displaystyle{ \left(\sqrt{1/21},\ \sqrt{1/15},\ \sqrt{1/10},\ \sqrt{1/6},\ -2\sqrt{1/3},\ 0\right) }[/math]

[math]\displaystyle{ \left(\sqrt{1/21},\ \sqrt{1/15},\ \sqrt{1/10},\ -\sqrt{3/2},\ 0,\ 0\right) }[/math]

[math]\displaystyle{ \left(\sqrt{1/21},\ \sqrt{1/15},\ -2\sqrt{2/5},\ 0,\ 0,\ 0\right) }[/math]

[math]\displaystyle{ \left(\sqrt{1/21},\ -\sqrt{5/3},\ 0,\ 0,\ 0,\ 0\right) }[/math]

[math]\displaystyle{ \left(-\sqrt{12/7},\ 0,\ 0,\ 0,\ 0,\ 0\right) }[/math]

The vertices of the 6-simplex can be more simply positioned in 7-space as permutations of:

(0,0,0,0,0,0,1)

This construction is based on facets of the 7-orthoplex.

Images

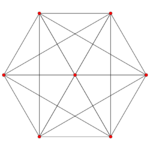
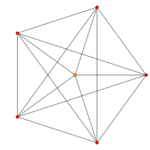
orthographic projections

Ak Coxeter plane	A6	A5	A4
Graph
Dihedral symmetry	[7]	[6]	[5]
Ak Coxeter plane	A3	A2
Graph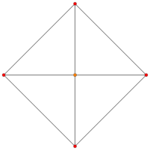
Dihedral symmetry	[4]	[3]

Related uniform 6-polytopes

The regular 6-simplex is one of 35 uniform 6-polytopes based on the [3,3,3,3,3] Coxeter group, all shown here in A₆ Coxeter plane orthographic projections.

References

• Coxeter, H.S.M.:
  •   (1973). "Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n≥5)". Regular Polytopes (3rd ed.). Dover. pp. 296. ISBN 0-486-61480-8. 
  • Sherk, F. Arthur; McMullen, Peter; Thompson, Anthony C. et al., eds (1995). Kaleidoscopes: Selected Writings of H.S.M. Coxeter. Wiley. ISBN 978-0-471-01003-6. https://books.google.com/books?id=fUm5Mwfx8rAC&pg=PP1. 
    • (Paper 22)   (1940). "Regular and Semi Regular Polytopes I". Math. Zeit. 46: 380–407. doi:10.1007/BF01181449. https://books.google.com/books?id=fUm5Mwfx8rAC&pg=PA251. 
    • (Paper 23)   (1985). "Regular and Semi-Regular Polytopes II". Math. Zeit. 188 (4): 559–591. doi:10.1007/BF01161657. https://books.google.com/books?id=fUm5Mwfx8rAC&pg=PA279. 
    • (Paper 24)   (1988). "Regular and Semi-Regular Polytopes III". Math. Zeit. 200: 3–45. doi:10.1007/BF01161745. https://books.google.com/books?id=fUm5Mwfx8rAC&pg=PA313. 
• Conway, John H.; Burgiel, Heidi; Goodman-Strauss, Chaim (2008). "26. Hemicubes: 1_n1". The Symmetries of Things. pp. 409. ISBN 978-1-56881-220-5. 
• Johnson, Norman (1991). Uniform Polytopes. Norman Johnson (mathematician). 
  • Johnson, N.W. (1966). The Theory of Uniform Polytopes and Honeycombs (PhD). University of Toronto. OCLC 258527038.

External links

• Olshevsky, George. "Simplex". Glossary for Hyperspace. Archived from the original on 4 February 2007. https://web.archive.org/web/20070204075028/members.aol.com/Polycell/glossary.html#Simplex. 
• Polytopes of Various Dimensions
• Multi-dimensional Glossary