Biology:Calibration curve

Short description: Method for determining the concentration of a substance in an unknown sample

A calibration curve plot showing limit of detection (LOD), limit of quantification (LOQ), dynamic range, and limit of linearity (LOL).

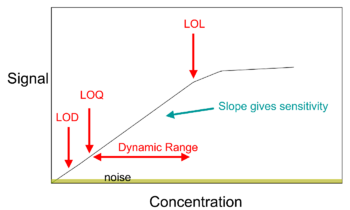
In analytical chemistry, a calibration curve, also known as a standard curve, is a general method for determining the concentration of a substance in an unknown sample by comparing the unknown to a set of standard samples of known concentration. A calibration curve is one approach to the problem of instrument calibration; other standard approaches may mix the standard into the unknown, giving an internal standard. The calibration curve is a plot of how the instrumental response, the so-called analytical signal, changes with the concentration of the analyte (the substance to be measured).

General use

In more general use, a calibration curve is a curve or table for a measuring instrument which measures some parameter indirectly, giving values for the desired quantity as a function of values of sensor output. For example, a calibration curve can be made for a particular pressure transducer to determine applied pressure from transducer output (a voltage). Such a curve is typically used when an instrument uses a sensor whose calibration varies from one sample to another, or changes with time or use; if sensor output is consistent the instrument would be marked directly in terms of the measured unit.

Method

The operator prepares a series of standards across a range of concentrations near the expected concentration of analyte in the unknown. The concentrations of the standards must lie within the working range of the technique (instrumentation) they are using. Analyzing each of these standards using the chosen technique will produce a series of measurements. For most analyses a plot of instrument response vs. concentration will show a linear relationship. The operator can measure the response of the unknown and, using the calibration curve, can interpolate to find the concentration of analyte.

An example of a standard curve showing the absorbance of different concentrations of protein (two trials for each measurement). The mass of protein in a different sample is determined by determining where on the standard curve it should go - in this case, 30 milligrams.

The data - the concentrations of the analyte and the instrument response for each standard - can be fit to a straight line, using linear regression analysis. This yields a model described by the equation y = mx + y₀, where y is the instrument response, m represents the sensitivity, and y₀ is a constant that describes the background. The analyte concentration (x) of unknown samples may be calculated from this equation.

Many different variables can be used as the analytical signal. For instance, chromium (III) might be measured using a chemiluminescence method, in an instrument that contains a photomultiplier tube (PMT) as the detector. The detector converts the light produced by the sample into a voltage, which increases with intensity of light. The amount of light measured is the analytical signal.

Example

Samples treated with the Bradford assay. The brown sample (lower absorbance) contains no protein, while the blue sample (higher absorbance) contains protein. The amount of protein in the second sample can be determined by comparison to a standard curve.

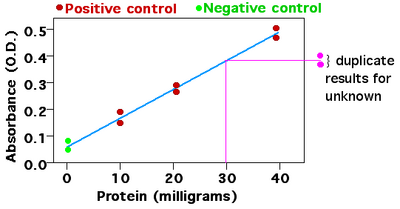
The Bradford assay is a colorimetric assay that measures protein concentration. The reagent Coomassie brilliant blue turns blue when it binds to arginine and aromatic amino acids present in proteins, thus increasing the absorbance of the sample. The absorbance is measured using a spectrophotometer, at the maximum absorbance frequency (A_max) of the blue dye (which is 595 nm). In this case, the greater the absorbance, the higher the protein concentration.

Data for known concentrations of protein are used to make the standard curve, plotting concentration on the X axis, and the assay measurement on the Y axis. The same assay is then performed with samples of unknown concentration. To analyze the data, one locates the measurement on the Y-axis that corresponds to the assay measurement of the unknown substance and follows a line to intersect the standard curve. The corresponding value on the X-axis is the concentration of substance in the unknown sample.

Error calculation

As expected, the concentration of the unknown will have some error which can be calculated from the formula below. This formula assumes that a linear relationship is observed for all the standards. It is important to note that the error in the concentration will be minimal if the signal from the unknown lies in the middle of the signals of all the standards (the term [math]\displaystyle{ y_\text{unk} - \bar{y} }[/math] goes to zero if [math]\displaystyle{ y_\text{unk} = \bar{y} }[/math])

[math]\displaystyle{ s_x = \frac{s_y}{|m|} \sqrt{\frac{1}{n} + \frac{1}{k} + \frac{(y_\text{unk}-\bar{y})^2}{m^2\sum_i{(x_i-\bar{x})^2}}} }[/math]

• [math]\displaystyle{ s_y = \sqrt{\frac{\sum_i {(y_i - m x_i-b)}^2}{n-2}} }[/math], is the standard deviation in the residuals
• [math]\displaystyle{ m }[/math] is the slope of the line
• [math]\displaystyle{ b }[/math] is the y-intercept of the line
• [math]\displaystyle{ n }[/math] is the number of standards
• [math]\displaystyle{ k }[/math] is the number of replicate unknowns
• [math]\displaystyle{ y_\text{unk} }[/math] is the measurement of the unknown
• [math]\displaystyle{ \bar{y} }[/math] is the average measurement of the standards
• [math]\displaystyle{ x_i }[/math] are the concentrations of the standards
• [math]\displaystyle{ \bar{x} }[/math] is the average concentration of the standards

Advantages and disadvantages

Most analytical techniques use a calibration curve. There are a number of advantages to this approach. First, the calibration curve provides a reliable way to calculate the uncertainty of the concentration calculated from the calibration curve (using the statistics of the least squares line fit to the data).

Second, the calibration curve provides data on an empirical relationship. The mechanism for the instrument's response to the analyte may be predicted or understood according to some theoretical model, but most such models have limited value for real samples. (Instrumental response is usually highly dependent on the condition of the analyte, solvents used and impurities it may contain; it could also be affected by external factors such as pressure and temperature.)

Many theoretical relationships, such as fluorescence, require the determination of an instrumental constant anyway, by analysis of one or more reference standards; a calibration curve is a convenient extension of this approach. The calibration curve for a particular analyte in a particular (type of) sample provides the empirical relationship needed for those particular measurements.

The chief disadvantages are (1) that the standards require a supply of the analyte material, preferably of high purity and in known concentration, and (2) that the standards and the unknown are in the same matrix. Some analytes - e.g., particular proteins - are extremely difficult to obtain pure in sufficient quantity. Other analytes are often in complex matrices, e.g., heavy metals in pond water. In this case, the matrix may interfere with or attenuate the signal of the analyte. Therefore, a comparison between the standards (which contain no interfering compounds) and the unknown is not possible. The method of standard addition is a way to handle such a situation.

Applications

• Analysis of concentration
• Verifying the proper functioning of an analytical instrument or a sensor device such as an ion selective electrode
• Determining the basic effects of a control treatment (such as a dose-survival curve in clonogenic assay)

See also

• Color
• Curve fitting
• Linear regression
• Logarithmic scale
• Protein
• Serial dilution

Bibliography

• Harris, Daniel Charles (2003). Quantitative chemical analysis. San Francisco: W.H. Freeman. ISBN 0-7167-4464-3. 
• Skoog, Douglas A.; Holler, F. James; Crouch, Stanley R. (2007). Principles of Instrumental Analysis. Pacific Grove: Brooks Cole. pp. 1039. ISBN 978-0-495-01201-6. 
• "A statistical overview on univariate calibration, inverse regression, and detection limits: Application to gas chromatography/mass spectrometry technique". Mass Spectrometry Reviews 26 (1): 1–18. 2007. doi:10.1002/mas.20100. PMID 16788893. Bibcode: 2007MSRv...26....1L.